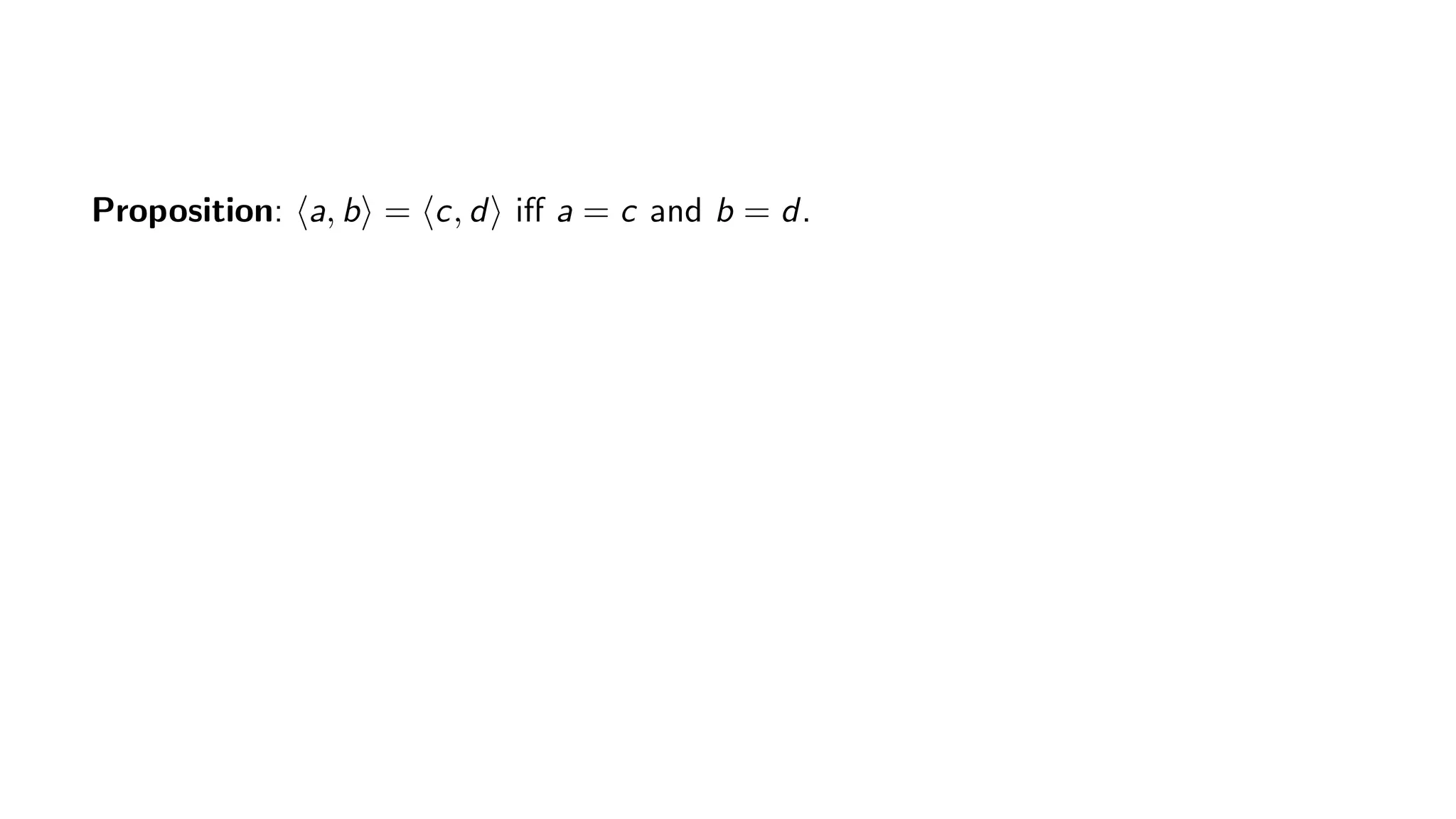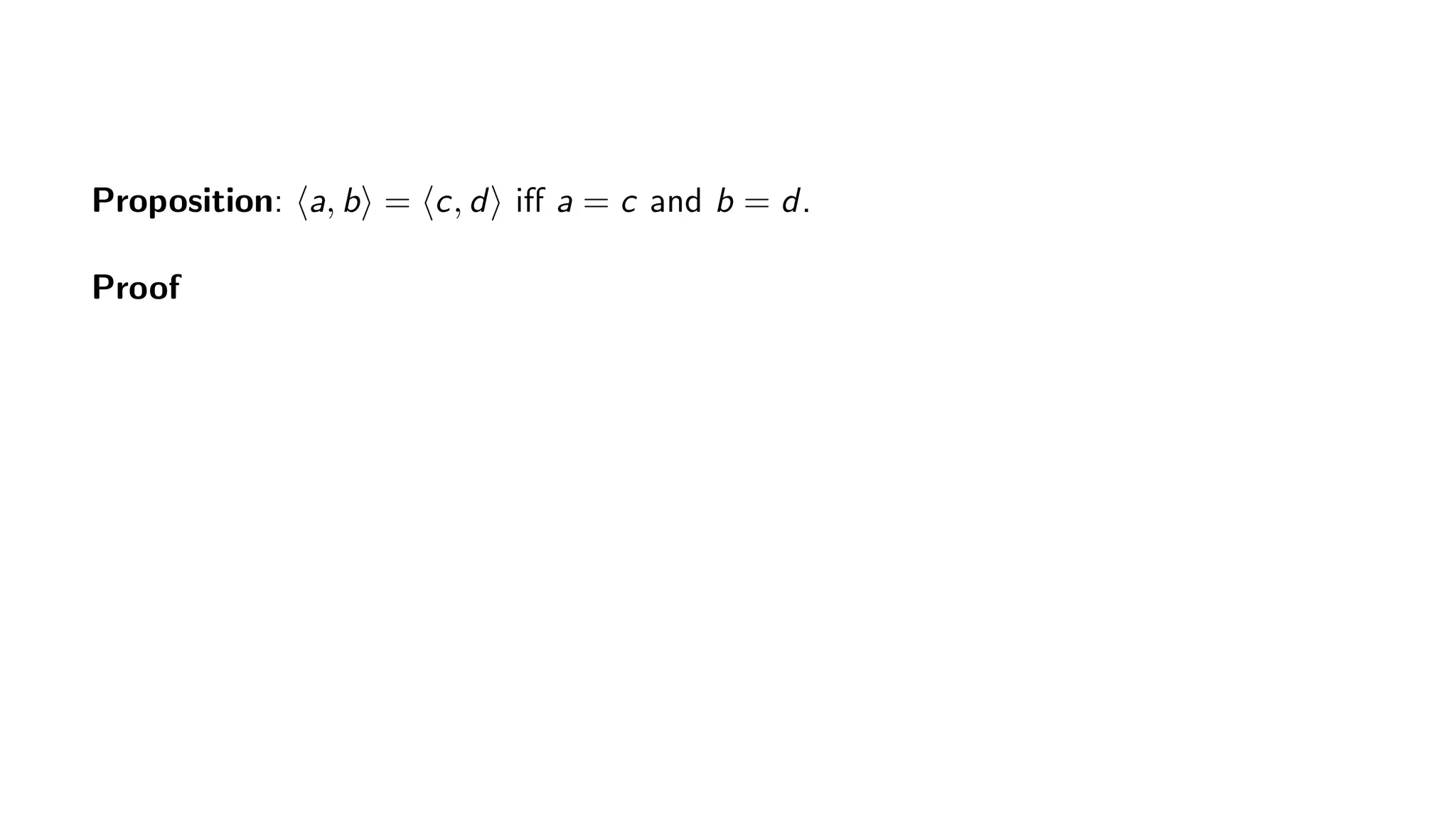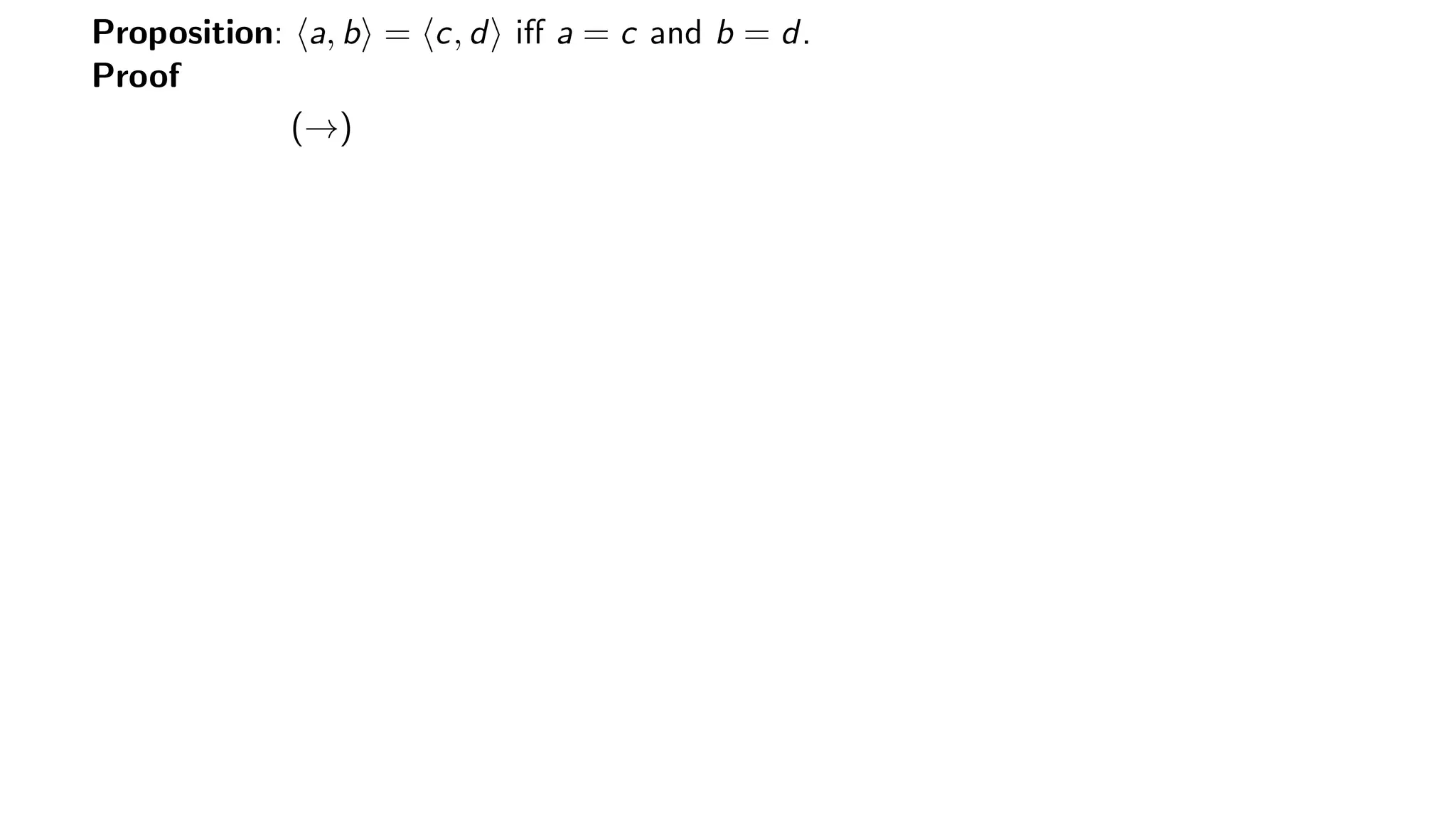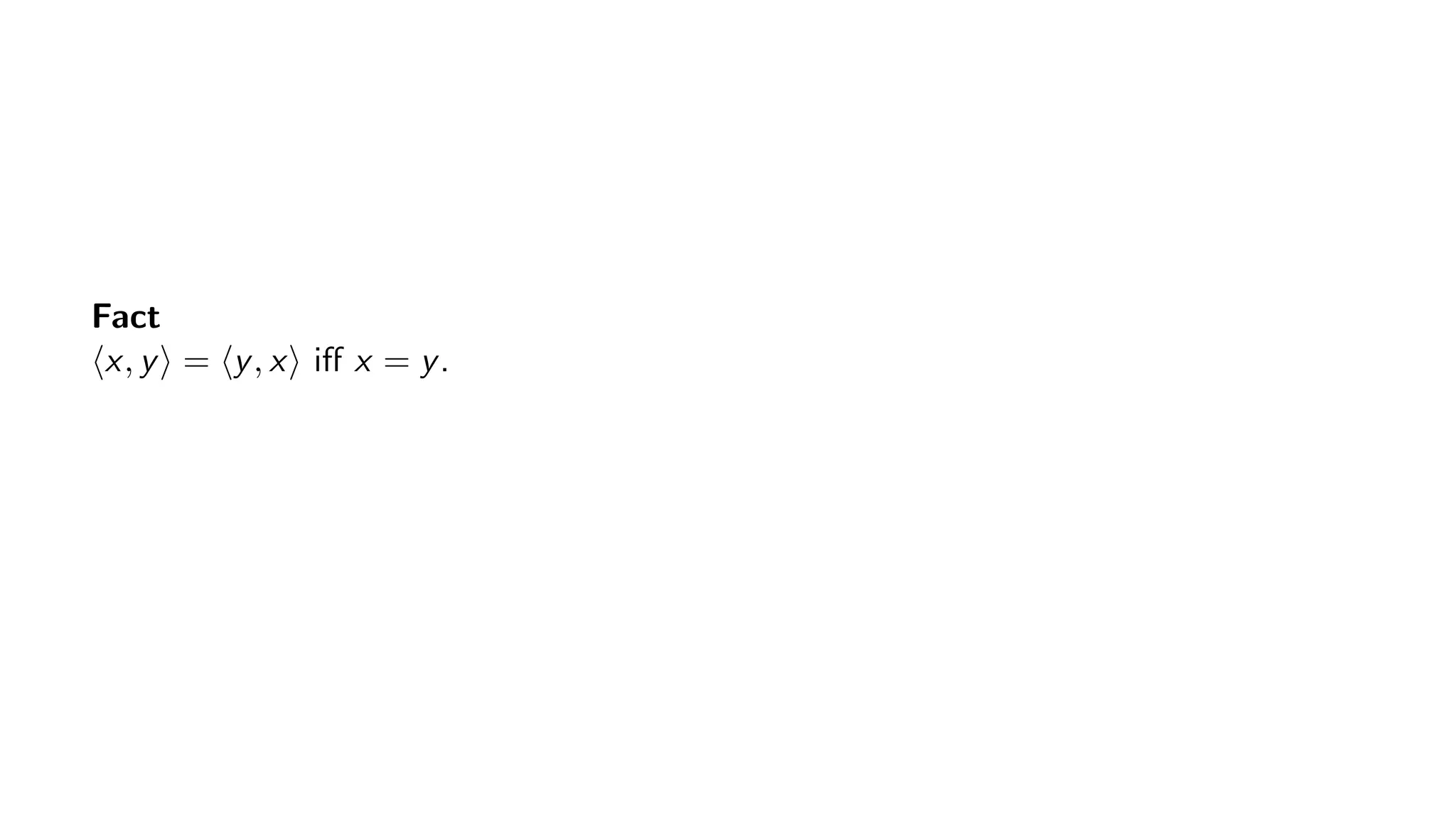The document provides a comprehensive introduction to set theory, emphasizing ordered pairs and their mathematical properties. It details the definition, significance, and proof of propositions relating to ordered pairs, highlighting their structure and equality criteria. Additionally, the text discusses the conceptualization of program variables in terms of their values and memory addresses.

1. Introduction to set theory and to methodology and philosophy of
mathematics and computer programming
Ordered pairs
An overview
by Jan Plaza
c 2017 Jan Plaza
Use under the Creative Commons Attribution 4.0 International License
Version of February 14, 2017

2. {x, y} – an unordered pair.
{x, y} = {y, x} – not so with ordered pairs.
A point on the plane is represented as an ordered pair of real numbers.
6
-
r
5
3
5, 3
5, 3 = 3, 5

3. Definition (Kuratowski)
The ordered pair with coordinates x, y , denoted x, y , is the set {{x}, {x, y}}
{x, y} tells that x and y are the components of the ordered pair.
{x} distinguishes the first component.
Fact
x, x = {{x}, {x, x}} = {{x}, {x}} = {{x}}

4. Proposition: a, b = c, d iff a = c and b = d.

5. Proposition: a, b = c, d iff a = c and b = d.
Proof

6. Proposition: a, b = c, d iff a = c and b = d.
Proof
(←)
(→)

7. Proposition: a, b = c, d iff a = c and b = d.
Proof
(←) Obvious.
(→)

8. Proposition: a, b = c, d iff a = c and b = d.
Proof
(←) Obvious.
(If the first object is known under the names a and c, and the second
object is known under the names b and d, then a, b and c, d are
ordered pairs formed from the same objects, and they are the same.)
(→)

9. Proposition: a, b = c, d iff a = c and b = d.
Proof
(←) Obvious.
(If the first object is known under the names a and c, and the second
object is known under the names b and d, then a, b and c, d are
ordered pairs formed from the same objects, and they are the same.)
(→) on the next slide

10. Proposition: a, b = c, d iff a = c and b = d.
Proof
(→)

11. Proposition: a, b = c, d iff a = c and b = d.
Proof
(→) Assume that a, b = c, d .

12. Proposition: a, b = c, d iff a = c and b = d.
Proof
(→) Assume that a, b = c, d .
Case: a = b.
Case: a=b.

13. Proposition: a, b = c, d iff a = c and b = d.
Proof
(→) Assume that a, b = c, d .
Case: a = b.
a, b = c, d .
Case: a=b.

14. Proposition: a, b = c, d iff a = c and b = d.
Proof
(→) Assume that a, b = c, d .
Case: a = b.
a, b = c, d .
So, {{a}} = {{c}, {c, d}}.
Case: a=b.

15. Proposition: a, b = c, d iff a = c and b = d.
Proof
(→) Assume that a, b = c, d .
Case: a = b.
a, b = c, d .
So, {{a}} = {{c}, {c, d}}.
So, {a} = {c} = {c, d}.
Case: a=b.

16. Proposition: a, b = c, d iff a = c and b = d.
Proof
(→) Assume that a, b = c, d .
Case: a = b.
a, b = c, d .
So, {{a}} = {{c}, {c, d}}.
So, {a} = {c} = {c, d}.
So, a = c = d.
Case: a=b.

17. Proposition: a, b = c, d iff a = c and b = d.
Proof
(→) Assume that a, b = c, d .
Case: a = b.
a, b = c, d .
So, {{a}} = {{c}, {c, d}}.
So, {a} = {c} = {c, d}.
So, a = c = d.
Case: a=b.
a, b = c, d .

18. Proposition: a, b = c, d iff a = c and b = d.
Proof
(→) Assume that a, b = c, d .
Case: a = b.
a, b = c, d .
So, {{a}} = {{c}, {c, d}}.
So, {a} = {c} = {c, d}.
So, a = c = d.
Case: a=b.
a, b = c, d .
So, {{a}, {a, b}} = {{c}, {c, d}}.

19. Proposition: a, b = c, d iff a = c and b = d.
Proof
(→) Assume that a, b = c, d .
Case: a = b.
a, b = c, d .
So, {{a}} = {{c}, {c, d}}.
So, {a} = {c} = {c, d}.
So, a = c = d.
Case: a=b.
a, b = c, d .
So, {{a}, {a, b}} = {{c}, {c, d}}.
a=b.

20. Proposition: a, b = c, d iff a = c and b = d.
Proof
(→) Assume that a, b = c, d .
Case: a = b.
a, b = c, d .
So, {{a}} = {{c}, {c, d}}.
So, {a} = {c} = {c, d}.
So, a = c = d.
Case: a=b.
a, b = c, d .
So, {{a}, {a, b}} = {{c}, {c, d}}.
a=b.
So, {a, b}={c}.

21. Proposition: a, b = c, d iff a = c and b = d.
Proof
(→) Assume that a, b = c, d .
Case: a = b.
a, b = c, d .
So, {{a}} = {{c}, {c, d}}.
So, {a} = {c} = {c, d}.
So, a = c = d.
Case: a=b.
a, b = c, d .
So, {{a}, {a, b}} = {{c}, {c, d}}.
a=b.
So, {a, b}={c}.
So, {a, b} = {c, d}.

22. Proposition: a, b = c, d iff a = c and b = d.
Proof
(→) Assume that a, b = c, d .
Case: a = b.
a, b = c, d .
So, {{a}} = {{c}, {c, d}}.
So, {a} = {c} = {c, d}.
So, a = c = d.
Case: a=b.
a, b = c, d .
So, {{a}, {a, b}} = {{c}, {c, d}}.
a=b.
So, {a, b}={c}.
So, {a, b} = {c, d}.
So, {c, d}={a}.

23. Proposition: a, b = c, d iff a = c and b = d.
Proof
(→) Assume that a, b = c, d .
Case: a = b.
a, b = c, d .
So, {{a}} = {{c}, {c, d}}.
So, {a} = {c} = {c, d}.
So, a = c = d.
Case: a=b.
a, b = c, d .
So, {{a}, {a, b}} = {{c}, {c, d}}.
a=b.
So, {a, b}={c}.
So, {a, b} = {c, d}.
So, {c, d}={a}.
So, {a} = {c}.

24. Proposition: a, b = c, d iff a = c and b = d.
Proof
(→) Assume that a, b = c, d .
Case: a = b.
a, b = c, d .
So, {{a}} = {{c}, {c, d}}.
So, {a} = {c} = {c, d}.
So, a = c = d.
Case: a=b.
a, b = c, d .
So, {{a}, {a, b}} = {{c}, {c, d}}.
a=b.
So, {a, b}={c}.
So, {a, b} = {c, d}.
So, {c, d}={a}.
So, {a} = {c}.
So, a = c.

25. Proposition: a, b = c, d iff a = c and b = d.
Proof
(→) Assume that a, b = c, d .
Case: a = b.
a, b = c, d .
So, {{a}} = {{c}, {c, d}}.
So, {a} = {c} = {c, d}.
So, a = c = d.
Case: a=b.
a, b = c, d .
So, {{a}, {a, b}} = {{c}, {c, d}}.
a=b.
So, {a, b}={c}.
So, {a, b} = {c, d}.
So, {c, d}={a}.
So, {a} = {c}.
So, a = c.
So, b = d.

26. Fact
x, y = y, x iff x = y.

27. Thinking about program variables and their values. (In two different ways.)
1. A variable has a value: VARIABLE-NAME, VALUE .
2. A variable refers to a memory address. The memory address stores a value.
VARIABLE-NAME, MEMORY-ADDRESS together with
MEMORY-ADDRESS, VALUE .