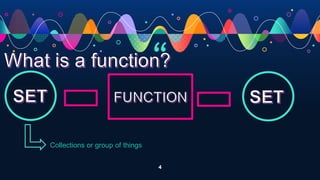
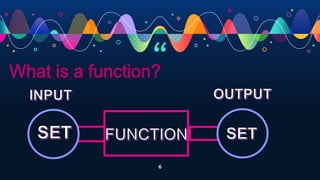
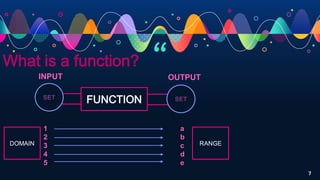
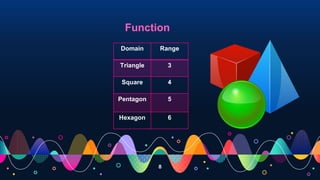
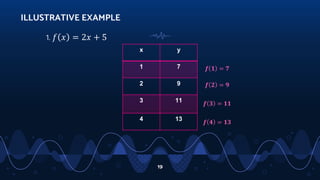
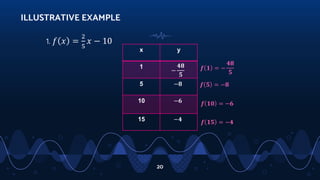
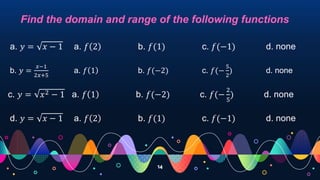
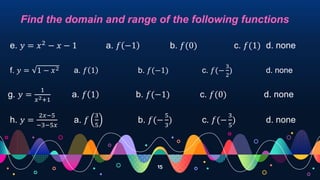
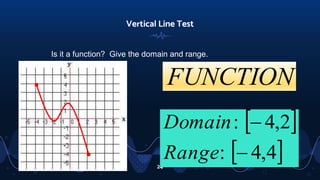
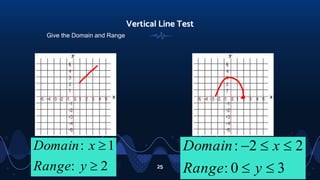
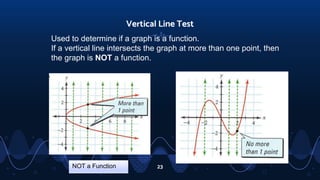
The document provides an overview of functions and their key concepts including: - Defining a function as a rule that assigns each element of one set (the domain) to an element of another set (the range). - Describing the domain as the set of inputs and the range as the set of outputs. - Explaining the vertical line test to determine if a relation is a function based on having a single output for each input. 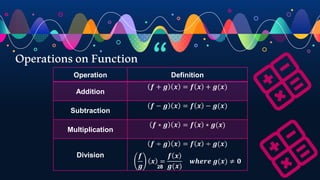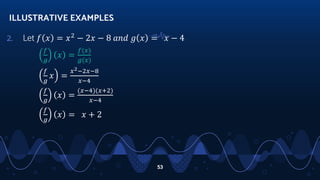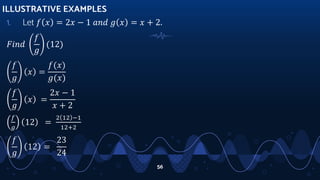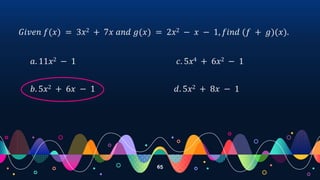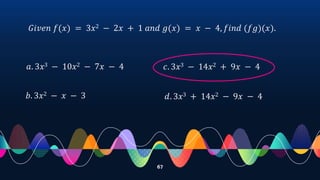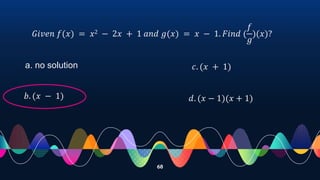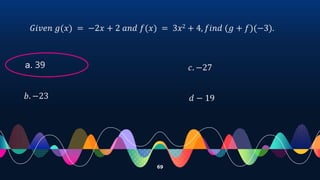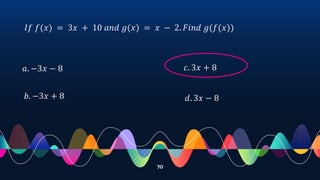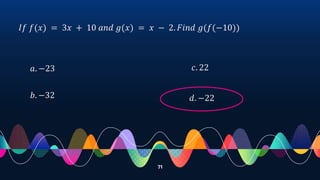- Demonstrating operations on functions such as addition, subtraction, multiplication and division through examples.

1. Marjorie B. Malveda
Instructor I
Functions

2. Our Learning Outcomes
• State the definition of a function
• Determine the domain and range of a function
• Perform the fundamental operations, Including composition, of functions
WHAT WE'LL COVER IN THIS SESSION

3. “
3
-refers to what something does

4. “
4
Collections or group of things

5. 1
3
5
a
c
d
e
𝟏, 𝟐, 𝟑, 𝟒, 𝟓 𝒂, 𝒃, 𝒄, 𝒅, 𝒆

6. “
6
What is a function?

7. “
7
What is a function?
FUNCTION
SET SET
INPUT OUTPUT
1
2
3
4
5
a
b
c
d
e
DOMAIN RANGE

8. 8
Function
Domain Range
Triangle 3
Square 4
Pentagon 5
Hexagon 6

9. 9
Function
x y
1 2
2 4
3 6
4 8
2x=y

10. 10
The FUNCTION is a relation such that no two
ordered pairs have the same first element. A
function usually denoted by 𝒚 = 𝒇(𝒙) is read as “f
of x”. A function may also be written as 𝒇: 𝒙 → 𝒚,
where 𝒙 ∈ domain and 𝒚 ∈ range

11. 11
The two types of functions that need explicit
restrictions are those with radicals and the rational
functions. The following illustrate the restrict of the
domain:
a. 𝑓 𝑥 = 2𝑥 − 1 is defined for 2𝑥 − 1 ≥ 0 or 𝑥 ≥
1
2
b. 𝑓 𝑥 =
1
𝑥−1
is defined for all real numbers ≠ 1
c. 𝑓 𝑥 =
1
𝑥2−1
is defined for all real number except ±1

12. 12
There are two methods in defining a Relation
a. Listing of ordered pairs
𝑓 𝑥 = 0,1 , 1,2 , 2,3 … … . .
b. Rule Method
𝑓 𝑥 = ȁ
(𝑥, 𝑦) 𝑦 = 𝑥 + 1, 𝑥 ∈ 𝑍

13. 13
Find the domain and range of the following functions
a. 𝑦 = 𝑥
e. 𝑦 = 𝑥 − 1
g. y =
𝑥−2
𝑥+1
b. 𝑦 = 𝑥 c. 𝑦 = 𝑥2
d. 𝑦 = 𝑥3 f. 𝑦 = 𝑥2 − 4

14. 14
Find the domain and range of the following functions
a. 𝑦 = 𝑥 − 1 a. 𝑓 2 b. 𝑓(1) c. 𝑓(−1) d. none
b. 𝑦 =
𝑥−1
2𝑥+5
a. 𝑓 1 b. 𝑓(−2) c. 𝑓(−
5
2
) d. none
c. 𝑦 = 𝑥2 − 1 a. 𝑓 1 b. 𝑓(−2) c. 𝑓(−
2
5
) d. none
d. 𝑦 = 𝑥 − 1 a. 𝑓 2 b. 𝑓(1) c. 𝑓(−1) d. none

15. 15
Find the domain and range of the following functions
e. 𝑦 = 𝑥2
− 𝑥 − 1 a. 𝑓 −1 b. 𝑓(0) c. 𝑓(1) d. none
f. 𝑦 = 1 − 𝑥2 a. 𝑓 1 b. 𝑓(−1) c. 𝑓(−
3
2
) d. none
g. 𝑦 =
1
𝑥2+1
a. 𝑓 1 b. 𝑓(−1) c. 𝑓(0) d. none
h. 𝑦 =
2𝑥−5
−3−5𝑥
a. 𝑓
3
5
b. 𝑓(−
5
3
) c. 𝑓(−
3
5
) d. none

16. “
16

17. 17
▹ is a rule of correspondence between to nonempty set of
elements, called the domain and range of the function, such
that to each element of the domain there corresponds one
and only element of the range, and each element of the
range is the correspondent at least one element of the
domain. A function is often called mapping and is said to
map its domain onto its range
FUNCTION

18. 18
1. 𝑓(𝑥)2
= 𝑦
ILLUSTRATIVE EXAMPLE
x y
1 1
2 4
3 9
4 16
𝒇 𝟏 = 𝟏
𝒇 𝟐 = 𝟒
𝒇 𝟑 = 𝟗
𝒇 𝟒 = 𝟏𝟔

19. 19
1. 𝑓 𝑥 = 2𝑥 + 5
ILLUSTRATIVE EXAMPLE
x y
1 7
2 9
3 11
4 13
𝒇 𝟏 = 𝟕
𝒇 𝟐 = 𝟗
𝒇 𝟑 = 𝟏𝟏
𝒇 𝟒 = 𝟏𝟑

20. 20
1. 𝑓 𝑥 =
2
5
𝑥 − 10
ILLUSTRATIVE EXAMPLE
x y
1
−
𝟒𝟖
𝟓
5 −𝟖
10 −𝟔
15 −𝟒
𝒇 𝟏 = −
𝟒𝟖
𝟓
𝒇 𝟓 = −𝟖
𝒇 𝟏𝟎 = −𝟔
𝒇 𝟏𝟓 = −𝟒

21. 21
ILLUSTRATIVE EXAMPLE
▹ For each x, there is
only one value of y.
▹ Therefore, it IS a
function.
Domain, x Range, y
1 -3.6
2 -3.6
3 4.2
4 4.2
5 10.7
6 12.1
52 52

22. 22
ILLUSTRATIVE EXAMPLE
▹ Is it a function? State the domain and range.
▹ No. The x-value of 5 is paired with two different y-
values.
▹ Domain: (5, 6, 3, 4, 12)
▹ Range: (8, 7, -1, 2, 9, -2)
{(5, 8), (6, 7), (3, -1), (4, 2), (5, 9), (12, -2)

23. 23
Vertical Line Test
Used to determine if a graph is a function.
If a vertical line intersects the graph at more than one point, then
the graph is NOT a function.
NOT a Function

24. 24
Vertical Line Test
Is it a function? Give the domain and range.
 
 
4
,
4
:
2
,
4
:
−
−
Range
Domain
FUNCTION

25. 25
Vertical Line Test
Give the Domain and Range
2
:
1
:


y
Range
x
Domain
3
0
:
2
2
:




−
y
Range
x
Domain

26. 26
Functional Notation
We have seen an equation written in the form y = some
expression in x.
Another way of writing this is to use functional notation.
For Example, you could write y = x²
as f(x) = x².

27. “
27
𝒇(𝒙)

28. “
28
OperationsonFunction
Operation Definition
Addition
𝒇 + 𝒈 𝒙 = 𝒇 𝒙 + 𝒈(𝒙)
Subtraction
𝒇 − 𝒈 𝒙 = 𝒇 𝒙 − 𝒈(𝒙)
Multiplication
𝒇 ∗ 𝒈 𝒙 = 𝒇 𝒙 ∗ 𝒈(𝒙)
Division
𝒇 ÷ 𝒈 𝒙 = 𝒇 𝒙 ÷ 𝒈(𝒙)
𝒇
𝒈
𝒙 =
𝒇 𝒙
𝒈(𝒙)
𝒘𝒉𝒆𝒓𝒆 𝒈(𝒙) ≠ 𝟎

29. “
29
Addition on Function
𝑓 + 𝑔 𝑥 = 𝑓 𝑥 + 𝑔(𝑥)

30. 1. Let 𝑓 𝑥 = 2𝑥 − 1 𝑎𝑛𝑑 𝑔 𝑥 = 𝑥 + 2
𝑓 + 𝑔 𝑥 = 𝑓 𝑥 + 𝑔 𝑥
𝑓 + 𝑔 𝑥 = 2𝑥 − 1 + (𝑥 + 2)
𝑓 + 𝑔 𝑥 = 3𝑥 + 1
ILLUSTRATIVE EXAMPLES
30

31. 2. Let 𝑓 𝑥 = 2𝑥2
− 4 𝑎𝑛𝑑 𝑔 𝑥 = 𝑥2
+ 4𝑥 − 2
𝑓 + 𝑔 𝑥 = 𝑓 𝑥 + 𝑔 𝑥
𝑓 + 𝑔 𝑥 = 2𝑥2
− 4 + (𝑥2
+ 4𝑥 − 2)
𝑓 + 𝑔 𝑥 = 3𝑥2
+ 4𝑥 − 6
ILLUSTRATIVE EXAMPLES
31

32. 3. Let 𝑓 𝑥 = 𝑥2
+ 2𝑥 − 1 𝑎𝑛𝑑 𝑔 𝑥 = 𝑥 − 5
𝑓 + 𝑔 𝑥 = 𝑓 𝑥 + 𝑔 𝑥
𝑓 + 𝑔 𝑥 = (𝑥2
+2𝑥 − 1) + (𝑥 − 5)
𝑓 + 𝑔 𝑥 = 𝑥2
+ 3𝑥 − 6
ILLUSTRATIVE EXAMPLES
32

33. Given f(x) = 4x – 1 and g(x) = 5x + 2, what is (f + g)(x)?
33
a) x + 4
b) x − 4
c) 9x + 1
d) 9x – 1

34. Given f(x) = 4x – 1 and g(x) = 5x + 2, what is (f + g)(x)?
34
a) x + 4
b) x − 4
c) 9x + 1
d) 9x – 1

35. 1. Let 𝑓 𝑥 = 2𝑥 − 1 𝑎𝑛𝑑 𝑔 𝑥 = 𝑥 + 2, .
𝐹𝑖𝑛𝑑 (𝑓 + 𝑔) 5 .
𝑓 + 𝑔 𝑥 = 𝑓 𝑥 + 𝑔 𝑥
𝑓 + 𝑔 𝑥 = 2𝑥 − 1 + (𝑥 + 2)
𝑓 + 𝑔 𝑥 = 3𝑥 + 1
(𝑓 + 𝑔) 5 = 3 5 + 1
(𝑓 + 𝑔) 5 = 16
ILLUSTRATIVE EXAMPLES
35

36. 2. Let 𝑓 𝑥 = 2𝑥2
− 4 𝑎𝑛𝑑 𝑔 𝑥 = 𝑥2
+ 4𝑥 − 2, .
𝐹𝑖𝑛𝑑 (𝑓 + 𝑔) −7
𝑓 + 𝑔 𝑥 = 𝑓 𝑥 + 𝑔 𝑥
𝑓 + 𝑔 𝑥 = 2𝑥2
− 4 + (𝑥2
+ 4𝑥 − 2)
𝑓 + 𝑔 𝑥 = 3𝑥2
+ 4𝑥 − 6
(𝑓 + 𝑔) −7 = 3(7)2
+ 4 7 − 6
(𝑓 + 𝑔) −7 = 147 + 28 − 6
(f + g) −7 = 169
ILLUSTRATIVE EXAMPLES
36

37. “
37
Subtraction on Function
𝑓 − 𝑔 𝑥 = 𝑓 𝑥 − 𝑔(𝑥)

38. 1. Let 𝑓 𝑥 = 2𝑥 − 1 𝑎𝑛𝑑 𝑔 𝑥 = 𝑥 + 2
𝑓 − 𝑔 𝑥 = 𝑓 𝑥 − 𝑔 𝑥
𝑓 − 𝑔 𝑥 = 2𝑥 − 1 − (𝑥 + 2)
𝑓 − 𝑔 𝑥 = 𝑥 − 3
ILLUSTRATIVE EXAMPLES
38

39. 2. Let 𝑓 𝑥 = 2𝑥2
− 4 𝑎𝑛𝑑 𝑔 𝑥 = 𝑥2
+ 4𝑥 − 2
𝑓 − 𝑔 𝑥 = 𝑓 𝑥 − 𝑔 𝑥
𝑓 − 𝑔 𝑥 = 2𝑥2
− 4 − (𝑥2
+ 4𝑥 − 2)
𝑓 − 𝑔 𝑥 = 𝑥2
− 4𝑥 − 2
ILLUSTRATIVE EXAMPLES
39

40. 3. Let 𝑓 𝑥 = 𝑥2
+ 2𝑥 − 1 𝑎𝑛𝑑 𝑔 𝑥 = 𝑥 − 5
𝑓 − 𝑔 𝑥 = 𝑓 𝑥 − 𝑔 𝑥
𝑓 − 𝑔 𝑥 = (𝑥2
+2𝑥 − 1) − (𝑥 − 5)
𝑓 − 𝑔 𝑥 = 𝑥2
+ 𝑥 + 4
ILLUSTRATIVE EXAMPLES
40

41. Given f(x) = 4x – 1 and g(x) = 5x + 2, what is (f - g)(x)?
41
a) x + 3
b) x − 5
c) 5x + 1
d) −x – 3

42. Given f(x) = 4x – 1 and g(x) = 5x + 2, what is (f - g)(x)?
42
a) x + 3
b) x − 5
c) 5x + 1
d) −x – 3

43. 1. Let 𝑓 𝑥 = 2𝑥 − 1 𝑎𝑛𝑑 𝑔 𝑥 = 𝑥 + 2.
Find (𝑓 − 𝑔)(−11).
𝑓 − 𝑔 𝑥 = 𝑓 𝑥 − 𝑔 𝑥
𝑓 − 𝑔 𝑥 = 2𝑥 − 1 − (𝑥 + 2)
𝑓 − 𝑔 𝑥 = 𝑥 − 3
𝑓 − 𝑔 −11 = −11 − 3
𝑓 − 𝑔 −11 = −14
ILLUSTRATIVE EXAMPLES
43

44. 2. Let 𝑓 𝑥 = 2𝑥2
− 4 𝑎𝑛𝑑 𝑔 𝑥 = 𝑥2
+ 4𝑥 − 2.
𝐹𝑖𝑛𝑑 (𝑓 − 𝑔)(21)
𝑓 − 𝑔 𝑥 = 𝑓 𝑥 − 𝑔 𝑥
𝑓 − 𝑔 𝑥 = 2𝑥2
− 4 − (𝑥2
+ 4𝑥 − 2)
𝑓 − 𝑔 𝑥 = 𝑥2
− 4𝑥 − 2
𝑓 − 𝑔 21 = (21)2
−4 21 − 2
𝑓 − 𝑔 21 = 441 − 84 − 2
𝑓 − 𝑔 21 = 355
ILLUSTRATIVE EXAMPLES
44

45. “
45
Multiplication on Function
𝑓 ∗ 𝑔 𝑥 = 𝑓 𝑥 ∗ 𝑔(𝑥)

46. 1. Let 𝑓 𝑥 = 2𝑥 − 1 𝑎𝑛𝑑 𝑔 𝑥 = 𝑥 + 2
𝑓 ∗ 𝑔 𝑥 = 𝑓 𝑥 ∗ 𝑔 𝑥
𝑓 ∗ 𝑔 𝑥 = 2𝑥 − 1 (𝑥 + 2)
𝑓 ∗ 𝑔 𝑥 = 2𝑥2
+ 3𝑥 − 2
ILLUSTRATIVE EXAMPLES
46

47. 2. Let 𝑓 𝑥 = 2𝑥2
− 4 𝑎𝑛𝑑 𝑔 𝑥 = 𝑥2
+ 4𝑥 − 2
𝑓 ∗ 𝑔 𝑥 = 𝑓 𝑥 ∗ 𝑔 𝑥
𝑓 ∗ 𝑔 𝑥 = 2𝑥2
− 4 (𝑥2
+ 4𝑥 − 2)
𝑓 ∗ 𝑔 𝑥 = 2𝑥4
+ 8𝑥3
− 4𝑥2
− 4𝑥2
− 16𝑥 + 8
𝑓 ∗ 𝑔 𝑥 = 2𝑥4
+ 8𝑥3
− 8𝑥2
− 16𝑥 + 8
ILLUSTRATIVE EXAMPLES
47

48. 3. Let 𝑓 𝑥 = 𝑥2
+ 2𝑥 − 1 𝑎𝑛𝑑 𝑔 𝑥 = 𝑥 − 5
𝑓 ∗ 𝑔 𝑥 = 𝑓 𝑥 ∗ 𝑔 𝑥
𝑓 ∗ 𝑔 𝑥 = (𝑥2
+2𝑥 − 1)(𝑥 − 5)
𝑓 ∗ 𝑔 𝑥 = 𝑥3
− 5𝑥2
+ 2𝑥2
− 10𝑥 − 𝑥 + 5
𝑓 ∗ 𝑔 𝑥 = 𝑥3
− 3𝑥2
− 11𝑥 + 5
ILLUSTRATIVE EXAMPLES
48

49. 49
Given f(x) = 3x – 2 and g(x) = 5x – 1, what
is (f g)(x)?
a) 15x2 − 13x + 2
b) 15x2 − 13x − 2
c) 15x2 − 7x + 2
d) 15x2 − 7x − 2

50. 1. Let 𝑓 𝑥 = 2𝑥 − 1 𝑎𝑛𝑑 𝑔 𝑥 = 𝑥 + 2, .
𝐹𝑖𝑛𝑑 (𝑓 ∗ 𝑔)(−14)
𝑓 ∗ 𝑔 𝑥 = 𝑓 𝑥 ∗ 𝑔 𝑥
𝑓 ∗ 𝑔 𝑥 = 2𝑥 − 1 (𝑥 + 2)
𝑓 ∗ 𝑔 𝑥 = 2𝑥2
+ 3𝑥 − 2
𝑓 ∗ 𝑔 −14 = 2(−14)2
+ 3 −14 − 2
𝑓 ∗ 𝑔 −14 = 392 − 52 − 2
𝑓 ∗ 𝑔 −14 = 338
ILLUSTRATIVE EXAMPLES
50

51. “
51
Division on Function
𝑓
𝑔
𝑥 =
𝑓(𝑥)
𝑔(𝑥)

52. 1. Let 𝑓 𝑥 = 2𝑥 − 1 𝑎𝑛𝑑 𝑔 𝑥 = 𝑥 + 2
𝑓
𝑔
𝑥 =
𝑓(𝑥)
𝑔(𝑥)
𝑓
𝑔
𝑥 =
2𝑥 − 1
𝑥 + 2
ILLUSTRATIVE EXAMPLES
52

53. 2. Let 𝑓 𝑥 = 𝑥2
− 2𝑥 − 8 𝑎𝑛𝑑 𝑔 𝑥 = 𝑥 − 4
𝑓
𝑔
𝑥 =
𝑓(𝑥)
𝑔(𝑥)
𝑓
𝑔
𝑥 =
𝑥2−2𝑥−8
𝑥−4
𝑓
𝑔
𝑥 =
(𝑥−4)(𝑥+2)
𝑥−4
𝑓
𝑔
𝑥 = 𝑥 + 2
ILLUSTRATIVE EXAMPLES
53

54. 3. Let 𝑓 𝑥 = 𝑥2
+ 2𝑥 − 1 𝑎𝑛𝑑 𝑔 𝑥 = 𝑥 − 5
𝑓
𝑔
𝑥 =
𝑓(𝑥)
𝑔(𝑥)
𝑓
𝑔
𝑥 =
𝑥2+2𝑥−1
𝑥−5
ILLUSTRATIVE EXAMPLES
54

55. 55
Given f(x) = 𝑥2
− 9 and g(x) = x + 3, what
is (
𝑓
𝑔
)(x)?
a) 𝑥 − 3
b) 𝑥 + 3
c)
𝑥2−9
𝑥+3
d) x2 − x − 6

56. 1. Let 𝑓 𝑥 = 2𝑥 − 1 𝑎𝑛𝑑 𝑔 𝑥 = 𝑥 + 2.
𝐹𝑖𝑛𝑑
𝑓
𝑔
(12)
𝑓
𝑔
𝑥 =
𝑓(𝑥)
𝑔(𝑥)
𝑓
𝑔
𝑥 =
2𝑥 − 1
𝑥 + 2
𝑓
𝑔
12 =
2 12 −1
12+2
𝑓
𝑔
12 =
23
24
ILLUSTRATIVE EXAMPLES
56

57. “
57
Composition on Function
𝑓°𝑔 𝑥 = 𝑓(𝑔 𝑥 )
Substituting one function to another

58. “
58
Composition on Function
Function Composition is just more substitution, very similar to
what we have been doing with finding the value of a function.
The difference is we will be substituting another function instead
of a number ...

59. “
59
Composition on Function
The term "composition of functions" (or "composite
function") refers to the combining together of two or
more functions in a manner where the output from
one function becomes the input for the next function.

60. “
60
Composition on Function
The notation used for composition is:
and is read "f composed with g of x"
or " f of g of x".
Notice how the letters stay in the
same order in each expression
for the composition.
The letters f (g(x)) tell you to
start with the function g (always
start with the function in the
innermost parentheses).

61. “
61
Composition on Function
Given the functions:
𝑓 𝑥 = 𝑥 + 1, 𝑔 𝑥 = 2𝑥
Find: (𝑓°𝑔)(𝑥)
(𝑓°𝑔) 𝑥 = 2x + 1

62. “
62
Composition on Function
Express 𝑔°𝑓 𝑥 𝑖𝑛 𝑡𝑒𝑟𝑚𝑠 𝑜𝑓 𝑥.
1. Given f (x) =𝑥 − 3 𝑎𝑛𝑑 𝑔 𝑥 = 𝑥2
+ 1
𝑔°𝑓 𝑥 = 𝑔(𝑓 𝑥 )
𝑓 𝑥 − 3 = (𝑥 − 3)2
+1
= 𝑥2
− 6𝑥 + 9 + 1
𝑔°𝑓 𝑥 = 𝑥2
− 6𝑥 + 10

63. “
63
Composition on Function
Express 𝑔°𝑓 −12 𝑖𝑛 𝑡𝑒𝑟𝑚𝑠 𝑜𝑓 𝑥
3. Given f (x) =𝑥 − 3 𝑎𝑛𝑑 𝑔 𝑥 = 𝑥2
+ 1
𝑔°𝑓 𝑥 = 𝑔(𝑓 𝑥 )
𝑓 𝑥 − 3 = (𝑥 − 3)2
+1
= 𝑥2
− 6𝑥 + 9 + 1
𝑔°𝑓 𝑥 = 𝑥2
− 6𝑥 + 10
(g°𝑓) −12 = (−12)2
−6 −12 + 10
(g°𝑓) −12 = 144 + 72 + 10
(g°𝑓) −12 = 226

64. 64

65. 65
𝐺𝑖𝑣𝑒𝑛 𝑓(𝑥) = 3𝑥2 + 7𝑥 𝑎𝑛𝑑 𝑔(𝑥) = 2𝑥2 − 𝑥 − 1, 𝑓𝑖𝑛𝑑 (𝑓 + 𝑔)(𝑥).
𝑎. 11𝑥2 − 1
𝑏. 5𝑥2 + 6𝑥 − 1
𝑐. 5𝑥4 + 6𝑥2 − 1
𝑑. 5𝑥2 + 8𝑥 − 1

66. 66
𝐺𝑖𝑣𝑒𝑛 𝑓(𝑥) = 3𝑥2 + 7𝑥 𝑎𝑛𝑑 𝑔(𝑥) = 2𝑥2 − 𝑥 − 1, 𝑓𝑖𝑛𝑑 (𝑓 − 𝑔)(𝑥).
𝑎. 𝑥2 + 8𝑥 + 1
𝑏. 5𝑥2 + 8𝑥 − 1
𝑐. 𝑥2 + 6𝑥 − 1
𝑑. 𝑥2 + 8𝑥 − 1

67. 67
𝐺𝑖𝑣𝑒𝑛 𝑓(𝑥) = 3𝑥2 − 2𝑥 + 1 𝑎𝑛𝑑 𝑔(𝑥) = 𝑥 − 4, 𝑓𝑖𝑛𝑑 (𝑓𝑔)(𝑥).
𝑎. 3𝑥3 − 10𝑥2 − 7𝑥 − 4
𝑏. 3𝑥2 − 𝑥 − 3
𝑐. 3𝑥3 − 14𝑥2 + 9𝑥 − 4
𝑑. 3𝑥3 + 14𝑥2 − 9𝑥 − 4

68. 68
𝐺𝑖𝑣𝑒𝑛 𝑓(𝑥) = 𝑥2 − 2𝑥 + 1 𝑎𝑛𝑑 𝑔(𝑥) = 𝑥 − 1. 𝐹𝑖𝑛𝑑 (
𝑓
𝑔
)(𝑥)?
a. no solution
𝑏. (𝑥 − 1)
𝑐. (𝑥 + 1)
𝑑. (𝑥 − 1)(𝑥 + 1)

69. 69
𝐺𝑖𝑣𝑒𝑛 𝑔(𝑥) = −2𝑥 + 2 𝑎𝑛𝑑 𝑓(𝑥) = 3𝑥2 + 4, 𝑓𝑖𝑛𝑑 (𝑔 + 𝑓)(−3).
a. 39
𝑏. −23
𝑐. −27
𝑑 − 19

70. 70
𝐼𝑓 𝑓(𝑥) = 3𝑥 + 10 𝑎𝑛𝑑 𝑔(𝑥) = 𝑥 − 2. 𝐹𝑖𝑛𝑑 𝑔(𝑓(𝑥))
𝑎. −3𝑥 − 8
𝑏. −3𝑥 + 8
𝑐. 3𝑥 + 8
𝑑. 3𝑥 − 8

71. 71
𝐼𝑓 𝑓(𝑥) = 3𝑥 + 10 𝑎𝑛𝑑 𝑔(𝑥) = 𝑥 − 2. 𝐹𝑖𝑛𝑑 𝑔(𝑓(−10))
𝑎. −23
𝑏. −32
𝑐. 22
𝑑. −22

72. “
72

73. A Function can be classified as Even, Odd or Neither. This
classification can be determined graphically or
algebraically.

74. Odd and Even Functions
▹ Even Functions
A function is "even"
when:
f(x) = f(−x) for all x
▹ Odd Functions
A function is "odd"
when:
−f(x) = f(−x) for all x
74

75. 1. Let 𝑓 𝑥 = 2𝑥 −
1 𝑎𝑛𝑑 𝑔 𝑥 = 𝑥 + 2
𝑓 + 𝑔 𝑥 = 𝑓 𝑥 + 𝑔 𝑥
𝑓 + 𝑔 𝑥
= 2𝑥 − 1 + (𝑥 + 2)
𝑓 + 𝑔 𝑥 = 3𝑥 + 1
ILLUSTRATIVE EXAMPLES
75
1. 𝑓 + 𝑔 𝑥 = 3𝑥 + 1
f(x) = f(−x)
𝑓 −𝑥 = 3 −𝑥 + 1
𝑓 −𝑥 = −3𝑥 + 1
𝑓 −𝑥 ≠ 𝑓 𝑥 ≠ −𝑓(𝑥)
Neither even nor odd

76. 𝐶ℎ𝑒𝑐𝑘𝑖𝑛𝑔:
𝑓 2 = 3 2 + 1
𝑓 2 = 7
𝑓 −2 = 3 −2 + 1
𝑓 −2 = −5
ILLUSTRATIVE EXAMPLES
76
2. 𝑓 + 𝑔 𝑥 = 3𝑥 + 1
f(x) = f(−x)
𝑓 −𝑥 = 3 −𝑥 + 1
𝑓 −𝑥 = −3𝑥 + 1
𝑓 −𝑥 ≠ 𝑓 𝑥 ≠ −𝑓(𝑥)
Neither even nor odd

77. 3. Let 𝑓 𝑥 = −𝑥2
+ 10
𝑓 −𝑥 = −(−𝑥)2
+ 10
𝑓 −𝑥 = −𝑥2
+ 10
𝑓 𝑥 = 𝑓 −𝑥
Even
ILLUSTRATIVE EXAMPLES
77
Let 𝑓 2 = −𝑥2
+ 10
𝑓 2 = −(2)2
+ 10
𝑓 2 = 6
𝑓 −2 = − −2 2
+ 10
𝑓 −2 = 6

78. 4. Let 𝑓 𝑥 = 𝑥3
+ 4𝑥
𝑓 −𝑥 = −(𝑥)3
+ 4(−𝑥)
𝑓 −𝑥 = −𝑥3
− 4x
𝑓 −𝑥 = −𝑓 𝑥
Odd
ILLUSTRATIVE EXAMPLES
78
Let 𝑓 2 = 𝑥3
+ 4𝑥
𝑓 2 = (2)3
+ 4(2)
𝑓 2 = 16
𝑓 −2 = − 2 3
+ 4(−2)
𝑓 −2 = −16

79. 5. Let 𝑓 𝑥 = −𝑥3
+ 5𝑥 − 2
𝑓 −𝑥 = −(𝑥)3
+ 5 −𝑥 − 2
𝑓 −𝑥 = −𝑥3
− 5𝑥 − 2
𝑓(𝑥) ≠ 𝑓 −𝑥 ≠ −𝑓 𝑥
Neither Even nor Odd
ILLUSTRATIVE EXAMPLES
79
Let 𝑓 2 = −𝑥3
+ 5𝑥 − 2
𝑓 2 = −(2)3
+ 5 2 − 2
𝑓 2 = 0
𝑓 −2 = − −2 3
+ 5 −2 − 2
𝑓 −2 = −4

80. ▹ A piecewise-defined function is a function that is defined by two or more
equations over a specified domain.
▹ The absolute value function
can be written as a piecewise-defined function.
▹ The basic characteristics of the absolute value function are summarized on the
next page.
PIECEWISE-DEFINED FUNCTION
80

81. Absolute Value Function is a Piecewise Function
81

82. Absolute Value Function is a Piecewise Function
82
◼ Evaluate the function when x = -1 and 0.

83. ▹ Evaluating piecewise functions is just like evaluating functions that you are
already familiar with.
▹ Let’s calculate f(2).
You are being asked to find y when
x = 2. Since 2 is  0, you will only substitute into the second part of the function.
Absolute Value Function is a Piecewise Function
83
f(x) =
x2 + 1 , x  0
x – 1 , x  0
f(2) = 2 – 1 = 1

84. ▹ Let’s calculate f(-2).
You are being asked to find y when
x = -2. Since -2 is  0, you will only substitute into the first part of the function.
▹ f(-2) = (-2)2 + 1 = 5
Absolute Value Function is a Piecewise Function
84
f(x) =
x2 + 1 , x  0
x – 1 , x  0

85. Your turn:
85
f(x) =
2x + 1, x  0
2x + 2, x  0
Evaluate the following:
f(-2) = -3
?
f(0) = 2
?
f(5) = 12
?
f(1) = 4
?

86. Your turn:
86
One more:
f(x) =
3x - 2, x  -2
-x , -2  x  1
x2 – 7x, x  1
Evaluate the following:
f(-2) = 2
?
f(-4) = -14
?
f(3) = -12
?
f(1) = -6
?