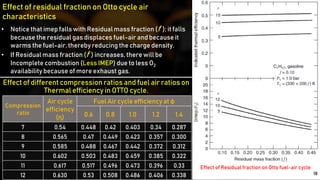
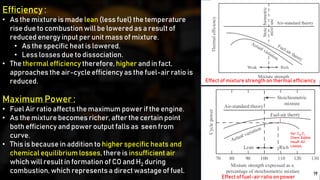
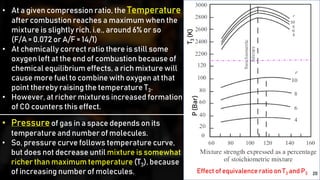
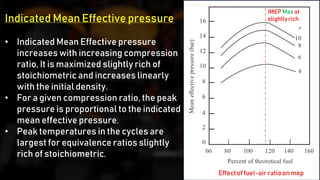
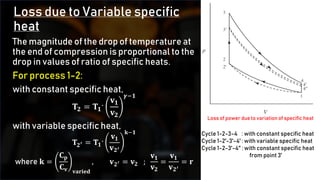
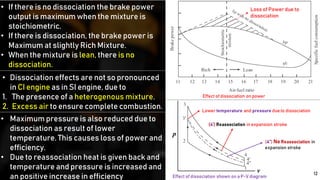
The fuel-air cycle provides a more accurate model of the actual thermodynamic cycle in an internal combustion engine compared to the air standard cycle by accounting for: 1) The actual composition of gases in the cylinder, which varies throughout the cycle. 2) Variations in specific heat and dissociation effects at high temperatures. 3) Changes in the number of moles as pressure and temperature fluctuate. 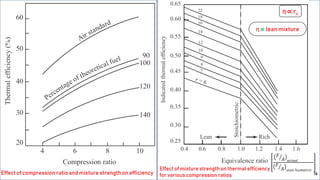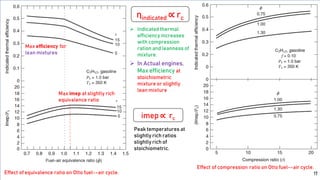The fuel-air cycle shows that efficiency is maximized with a slightly rich mixture near stoichiometric due to higher temperatures from dissociation. It also demonstrates efficiency gains from higher compression but losses from richer mixtures beyond stoichiometric due to incomplete combustion.

1. Fuel Air
Cycles
SOUMYTH

2. 2
• Theoretical cycle based on the actual properties of the cylinder contents is
called the fuel air cycle.
• The fuel air cycle takes into consideration the following.
1. The ACTUAL COMPOSITION of the cylinder contents.
2. The VARIATION OF SPECIFIC HEAT of the gases in the cylinder.
3. The DISSOCIATION EFFECT.
4. The VARIATION IN THE NUMBER OF MOLES present in the cylinder as the
pressure and temperature change.
• The fuel-air cycle analysis considers the following Assumptions:
1. Compression and expansion processes are frictionless.
2. No chemical changes in either fuel or prior to combustion.
3. Combustion takes place instantaneously at the Top Dead Centre.
4. All processes are Adiabatic.
5. The fuel is well mixed with Air.
6. Subsequent with combustion, the change is always in chemical equilibrium.
Introduction

3. 3
• Actual composition of the cylinder contents are
Fuel + Air + Water vapor + Residual gases.
• The fuel air ratio changes during the engine operation.
• The change in air fuel ratio affects the composition of gases
before and after combustion particularly the percentage of
CO2, CO, H2O etc.. in the exhaust gas.
• The amount of exhaust gases in the clearance volume varies
with speed and load on the engine.
• The fresh charge composition varies when it enters the
cylinder, because it comes in contact with the burnt gases.
Actual composition

4. 4
The Composition of Working fluid, which changes during the engine operating cycle, is indicated in the
following table.
Process SI Engine CI Engine
Intake
Air, Fuel, Recycled exhaust and Residual
gases.
Air, Recycled exhaust and Residual
gases.
Compression
Air, Fuel, Vapor, Recycled exhaust and
Exhaust gases.
Air, Recycled exhaust and Residual
gases.
Expansion
Composition products
(CO2, H2,O2, NO, OH, O, H, ..)
Composition products
(CO2, H2,O2, NO, OH, O, H, ..)
Exhaust
Composition products (Mainly N2, CO2, H2O)
If φ < 1 ⟶ O2 or φ > 1 ⟶CO2 & H2O.
Composition products
(Mainly N2, CO2, H2O)
• The effect of cylinder composition on the performance of the engine can easily
computed by means of suitable numerical techniques.
• Fuel-air analysis can be done more easily through computer rather than manual
calculations.

5. 5
Variable Specific Heat
• As the temperature increases, motion of molecules increases, part of
heat absorbed is utilized for producing motion of molecules. So more
heat is required to raise the temperature through one degree of unit
mass at higher levels i.e., higher specific heat at higher temperatures.
• All gases except mono-atomic gases, show an increase in specific
heat with temperature.
• The increase in specific heat does not follow any particular law.
However between the temperature range 300-1500K the specific heat
curve is nearly a straight line which may by approximately expressed
in form
Cp = a1 + k1T
Cv = b1 + k1T
where a1, b1 and k1 are constants and gas constant R = Cp - Cv = a1 – b1

6. 6
• Above 1500 K the specific heat increases is much more rapid and may be
expressed in the form.
Cp = a1 + k1T + k2T2
Cv = b1 + k1T + k2T2
Since the difference between Cp and Cv is constant, the value of k
decreases with increase in temperature.
k =
Cp
Cv
=
R + Cv
Cv
= 1 +
R
Cv
k ∝
1
T
Thus, if the variation of specific heats is taken in to account during the
compression stroke, the final temperature and pressure would be lower
compared to the value obtained at constant specific heat.
Variable Specific Heat

7. 7
The magnitude of the drop of temperature at
the end of compression is proportional to the
drop in values of ratio of specific heats.
For process 1-2:
with constant specific heat,
𝐓𝟐 = 𝐓𝟏·
𝐯 𝟏
𝐯 𝟐
𝜸−𝟏
with variable specific heat,
𝐓𝟐′ = 𝐓𝟏·
𝐯 𝟏
𝐯 𝟐′
𝐤−𝟏
where 𝐤 =
𝐂 𝐩
𝐂 𝐯 𝐯𝐚𝐫𝐢𝐞𝐝
, 𝐯 𝟐′ = 𝐯 𝟐 ;
𝐯 𝟏
𝐯 𝟐
=
𝐯 𝟏
𝐯 𝟐′
= 𝐫
Cycle 1-2-3-4 : with constant specific heat
Cycle 1-2'-3'-4' : with variable specific heat
Cycle 1-2-3'-4" : with constant specific heat
from point 3'
Loss due to Variable specific
heat
Loss of power due to variation of specific heat

8. 8
Process 2-3 : Constant volume combustion (Heat addition), from point 2’
will give a temperature T3’ with the variation in specific heat, instead of T3.
𝐦 𝐟 ⋅ 𝐐 𝐇𝐕 = 𝐂 𝐯 ⋅ 𝐓𝟑 − 𝐓𝟐 = 𝐂 𝐯′ ⋅ 𝐓𝟑′ − 𝐓𝟐′
As T2’ < T2 and Cv’ > Cv ⟶ T3’ < T3
Process 3’-4’’ : (Expansion with Constant specific Heat from point 3’)
𝐓𝟒′′ = 𝐓𝟑′·
𝐯 𝟑
𝐯 𝟒′′
𝜸−𝟏
Process 3’-4’ : (Expansion with Variable specific Heat from point 3’)
𝐓𝟒′ = 𝐓𝟑′·
𝐯 𝟑
𝐯 𝟒′
𝐤−𝟏
T4’ > T4’’ as the specific heat ratio increase with decrease in the
temperature. (k > γ)

9. 9
Dissociation
• Dissociation is the disintegration of combustion products at high
temperature above 1600 K.
• Dissociation is the reverse process to combustion. In Dissociation the
heat is absorbed whereas during combustion the heat is liberated.
• In IC engines, mainly dissociation of CO2 into CO and O2 occurs, whereas
there is a very little dissociation of H2O.
The dissociation of CO2 into CO and O2 starts commencing around 1000 OC.
2 CO2 ⟶ 2CO + O2 + Heat
The dissociation of H2O occurs at temperature above 1300 OC.
2 H2O ⟶ 2 H2 +O2 + Heat

10. 10
• The presence of CO and O2 in the gases tends to prevent the dissociation
of CO2, this is noticeable in a rich fuel mixture which by producing more
CO, suppresses dissociation of CO2.
• There is no dissociation in the burnt gases of a lean fuel air mixture, This
is mainly since the temperature produced is too low for this
phenomenon to occur.
• The maximum dissociation occurs in the burnt gases of the
chemically correct fuel-air mixture when the temperature are
expected to be high but decreases with the leaner and richer
mixtures.
Dissociation

11. 11
• Figure shows a typical curve that
indicates the reduction in the
temperature of the exhaust gas
mixtures due to dissociation with
respect to air-fuel ratio.
• With no dissociation, maximum
temperature is attained at
chemically correct air-fuel ratio.
With dissociation maximum
temperature is obtained when
mixture is slightly rich.
• Dissociation reduces the maximum
temperature by about 300 OC even at
the chemically correct air-fuel ratio.
Max. Temperature
with dissociation
Temperature
reduced due
to
dissociation

12. 12
• If there is no dissociation the brake power
output is maximum when the mixture is
stoichiometric.
• If there is dissociation, the brake power is
Maximum at slightly Rich Mixture.
• When the mixture is lean, there is no
dissociation.
• Dissociation effects are not so pronounced
in CI engine as in SI engine, due to
1. The presence of a heterogenous mixture.
2. Excess air to ensure complete combustion.
• Maximum pressure is also reduced due to
dissociation as result of lower
temperature. This causes loss of power and
efficiency.
• Due to reassociation heat is given back and
temperature and pressure is increased and
an positive increase in efficiency

13. 13
Effect of Number of Moles
• The number of molecules in the cylinder varies as the pressure and
temperature change.
• Number of molecules present in the cylinder after combustion depends
upon the
1. Fuel-air ratio,
2. Type and extend of reaction in the cylinder.
• Pressure inside the cylinder is directly proportional to Number of
Moles(n), Work done depends upon mean effective pressure (P),
So, Work done is proportional to Number of Moles of cylinder gases.

14. 14
Comparison of Air-Standard and Fuel-Air cycles
• By, Air standard cycle analysis, it is understood how the efficiency is improved
by increasing the compression ratio. Air standard cycle analysis doesn’t
consider the effect of fuel-air ratio on the thermal efficiency because the
working fluid was air.
• In general, fuel-air cycle is used to study
1. The effect of fuel-air ratio on engine thermal efficiency.
2. How the peak pressure and temperature during the cycle varying and its influence on
many engine operating variables.
• Fuel air cycle analysis suggests that the thermal efficiency will deteriorate as
the mixture supplied to the engine is enriched, because of losses due to
variable specific heat and dissociation as the mixture approaches chemically
correct values.
• Enrichment beyond chemically correct ratio leads to incomplete combustion
and loss in power.
• Thermal efficiency will increase as the mixture is made leaner. Beyond a
certain leaning, the combustion becomes erratic with loss of efficiency.
• In general the maximum efficiency is within the lean zone near the
stoichiometric ratio.

15. 15
Effect of Operating variables
• The effect of the common engine operating variables on the thermal
efficiency, pressure and temperature within the engine cylinder is
better understood by fuel-air analysis.
• The major operating variables
1. Compression ratio
2. Equivalence ratio
• The Equivalence Ratio, φ, is defined as ratio of actual fuel-air ratio to
chemically correct fuel-air ratio on mass basis.
• The fuel-air cycle efficiency increases with the compression ratio in the
same manner as the air-standard cycle efficiency, as there is more
scope of expansion work.
• The ratio of fuel-air cycle efficiency to air-standard efficiency is
independent of the compression ratio for a given equivalence ratio for
the constant-volume fuel-air cycle.

16. 16
Effect of mixture strength on thermal efficiency
for various compression ratiosEffect of compression ratio and mixture strength on efficiency
η ∝ rc
η ∝ lean mixture
𝐹
𝐴 𝑎𝑐𝑡𝑢𝑎𝑙
𝐹
𝐴 𝑠𝑡𝑜𝑖𝑐 ℎ𝑖𝑜𝑚𝑒𝑡𝑟𝑖𝑐

17. 17
ηindicated ∝ rc
imep ∝ rc
Peak temperatures at
slightly rich ratios
slightly rich of
stoichiometric.
➢ Indicated thermal
efficiency increases
with compression
ration and leanness of
mixture.
➢ In Actual engines,
Max efficiency at
stoichiometric
mixture or slightly
lean mixture

18. 18
Effect of residual fraction on Otto cycle air
characteristics
Effect of Residual fraction on Otto fuel-air cycle
• Notice that imep falls with Residual mass fraction (f ); it falls
because the residual gas displaces fuel-air and because it
warms the fuel-air, thereby reducing the charge density.
• If Residual mass fraction (f ) increases, there will be
Incomplete combustion (Less IMEP) due to less O2
availability because of more exhaust gas.
Effect of different compression ratios and fuel air ratios on
Thermal efficiency in OTTO cycle.
Compression
ratio
Air cycle
efficiency
(η)
Fuel Air cycle efficiency at φ
0.6 0.8 1.0 1.2 1.4
7 0.54 0.448 0.42 0.403 0.34 0.287
8 0.565 0.47 0.449 0.423 0.357 0.300
9 0.585 0.488 0.467 0.442 0.372 0.312
10 0.602 0.503 0.483 0.459 0.385 0.322
11 0.617 0.517 0.496 0.473 0.396 0.33
12 0.630 0.53 0.508 0.486 0.406 0.338

19. Efficiency :
• As the mixture is made lean (less fuel) the temperature
rise due to combustion will be lowered as a result of
reduced energy input per unit mass of mixture.
• As the specific heat is lowered.
• Less losses due to dissociation.
• The thermal efficiency therefore, higher and in fact,
approaches the air-cycle efficiency as the fuel-air ratio is
reduced. Effect of mixture strength on thermal efficiency
Effect of fuel-air ratio on power
19
Maximum Power :
• Fuel Air ratio affects the maximum power if the engine.
• As the mixture becomes richer, after the certain point
both efficiency and power output falls as seen from
curve.
• This is because in addition to higher specific heats and
chemical equilibrium losses, there is insufficient air
which will result in formation of CO and H2 during
combustion, which represents a direct wastage of fuel.
Var. Cp, Cv
Chem. Eqlbm
Insuff. Air
Losses

20. • At a given compression ratio, the Temperature
after combustion reaches a maximum when the
mixture is slightly rich. i.e., around 6% or so
(F/A = 0.072 or A/F = 14/1)
• At chemically correct ratio there is still some
oxygen left at the end of combustion because of
chemical equilibrium effects, a rich mixture will
cause more fuel to combine with oxygen at that
point thereby raising the temperature T3.
• However, at richer mixtures increased formation
of CO counters this effect.
T3(K)
P(Bar)
Effect of equivalence ratio on T3 and P3
• Pressureof gas in a space depends on its
temperature and number of molecules.
• So, pressure curve follows temperature curve,
but does not decrease until mixture is somewhat
richer than maximum temperature (T3), because
of increasing number of molecules. 20

21. Exhaust gas Temp
• The behaviour of T4 (Exhaust gas Temp.)
with compression ratio is different from T3
(After combustion temp.).
• Unlike T3, the exhaust gas temperature T4
is lower at high compression ratios,
because the increased expansion causes
the gas to do more work and less heat to be
rejected at the end of stroke.
• The same effect is present in the case of Air
cycle analysis.
• Only at stoichiometric mixture, Less loses
and fuel is utilized completely to give
higher Exhaust temperature.
21

22. Indicated Mean Effective pressure
• Indicated Mean Effective pressure
increases with increasing compression
ratio, It is maximized slightly rich of
stoichiometric and increases linearly
with the initial density.
• For a given compression ratio, the peak
pressure is proportional to the indicated
mean effective pressure.
• Peak temperatures in the cycles are
largest for equivalence ratios slightly
rich of stoichiometric.
22

23. 23
Effect of Fuel Type Vs. IMEP on Otto Fuel-Air cycle
Gasoline C3H17
10 0.44 13.3
15 0.495 14.4
Diesel C14.4H24.9
10 0.44 13.7
15 0.495 14.9
Methane CH4
10 0.44 12.2
15 0.496 13.1
Methanol CH3OH
10 0.43 13.1
15 0.48 14.2
Nitromethane CH3NO2
10 0.39 21.0
15 0.43 23.1
Nitromethane is an excellent choice for racing fuel, as it has the
largest IMEP of Fuels