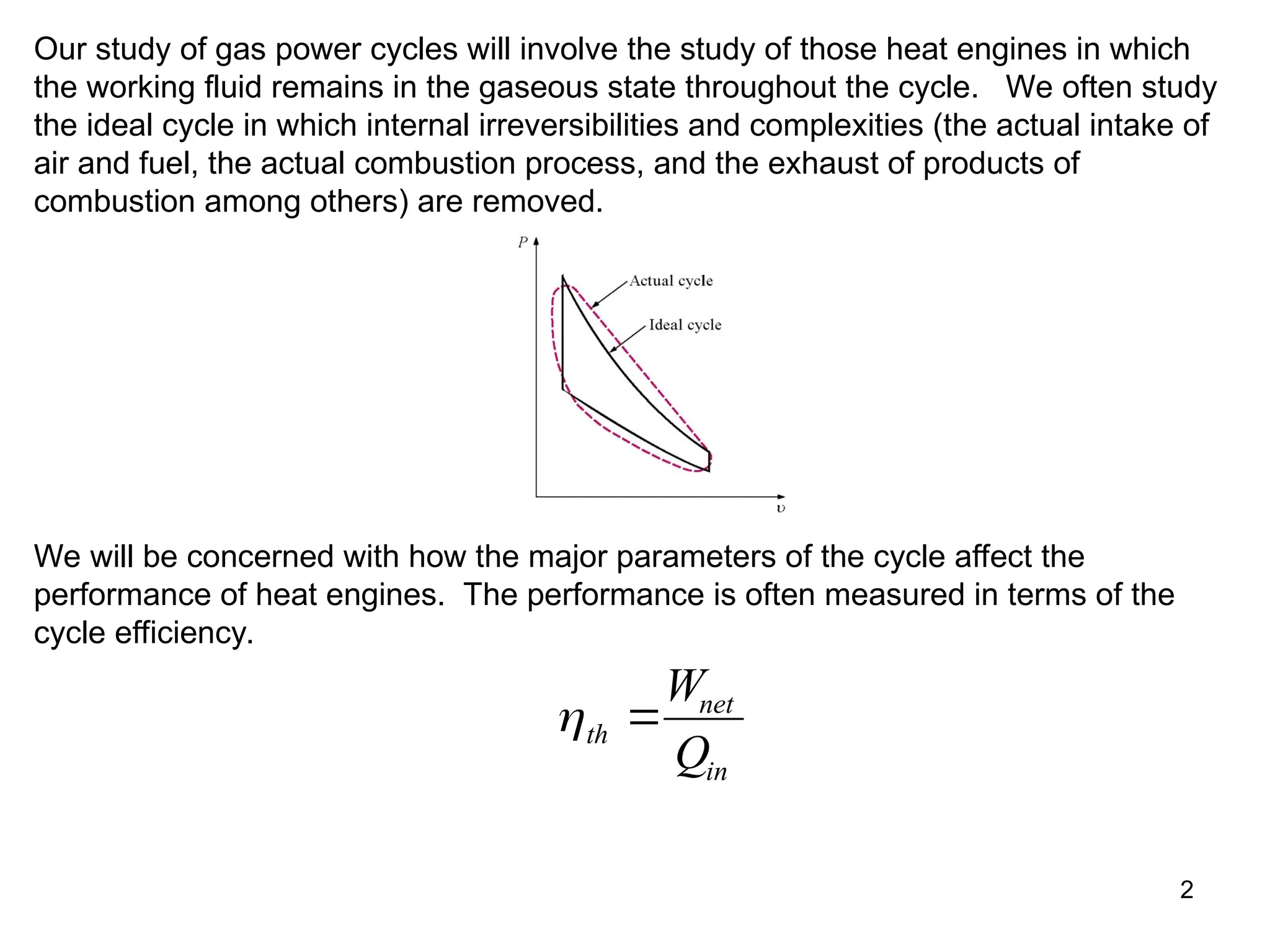
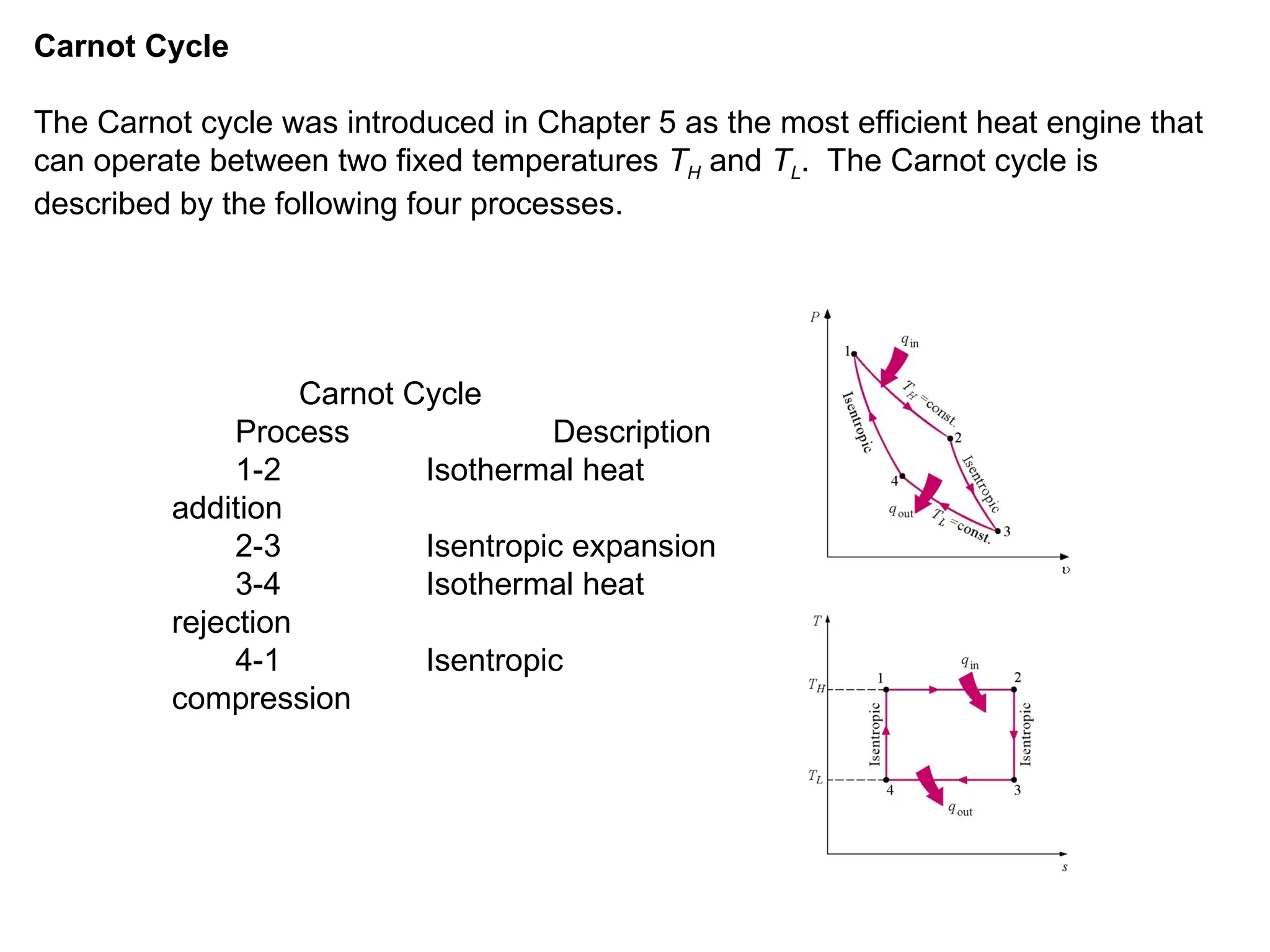
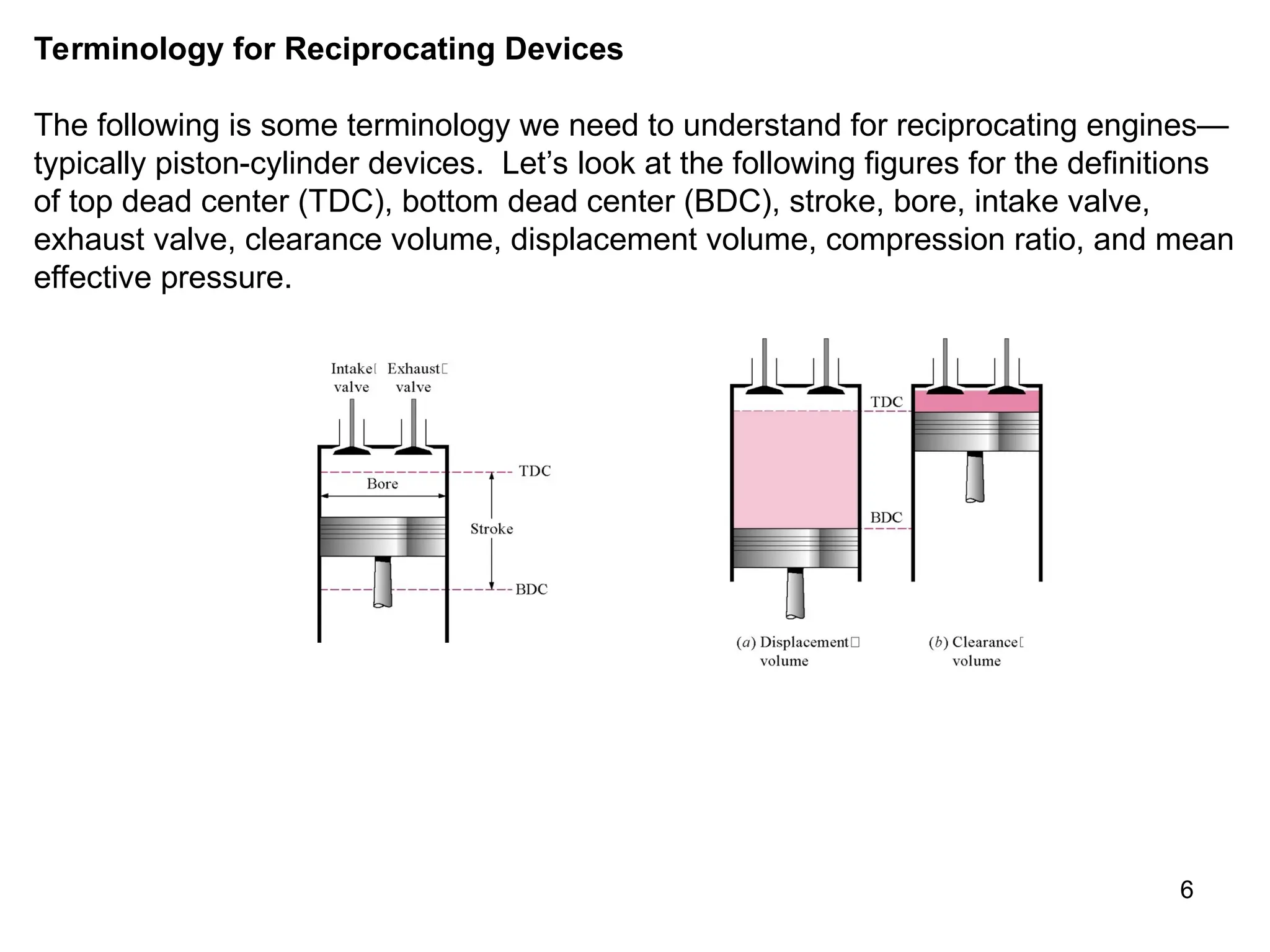
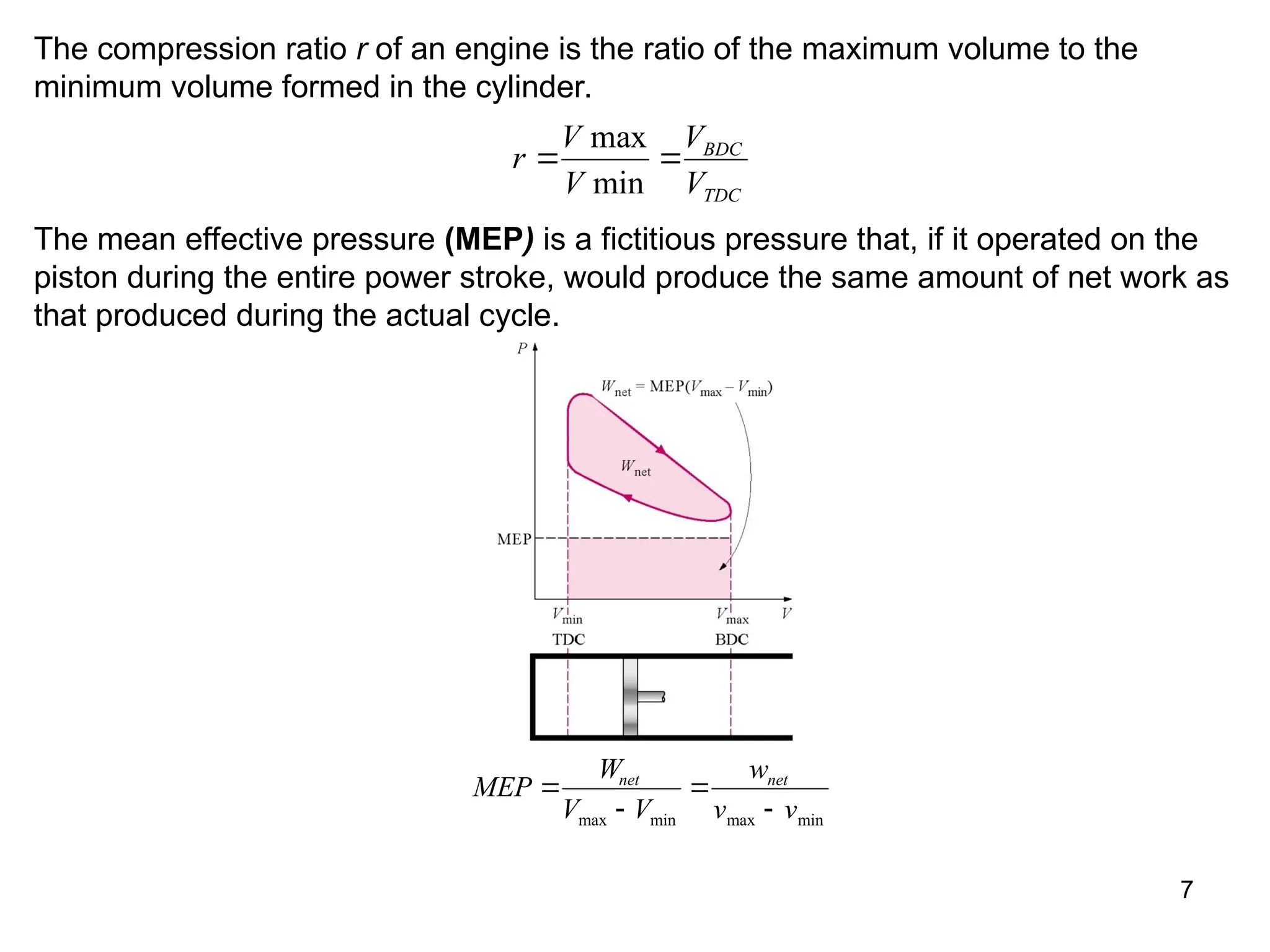
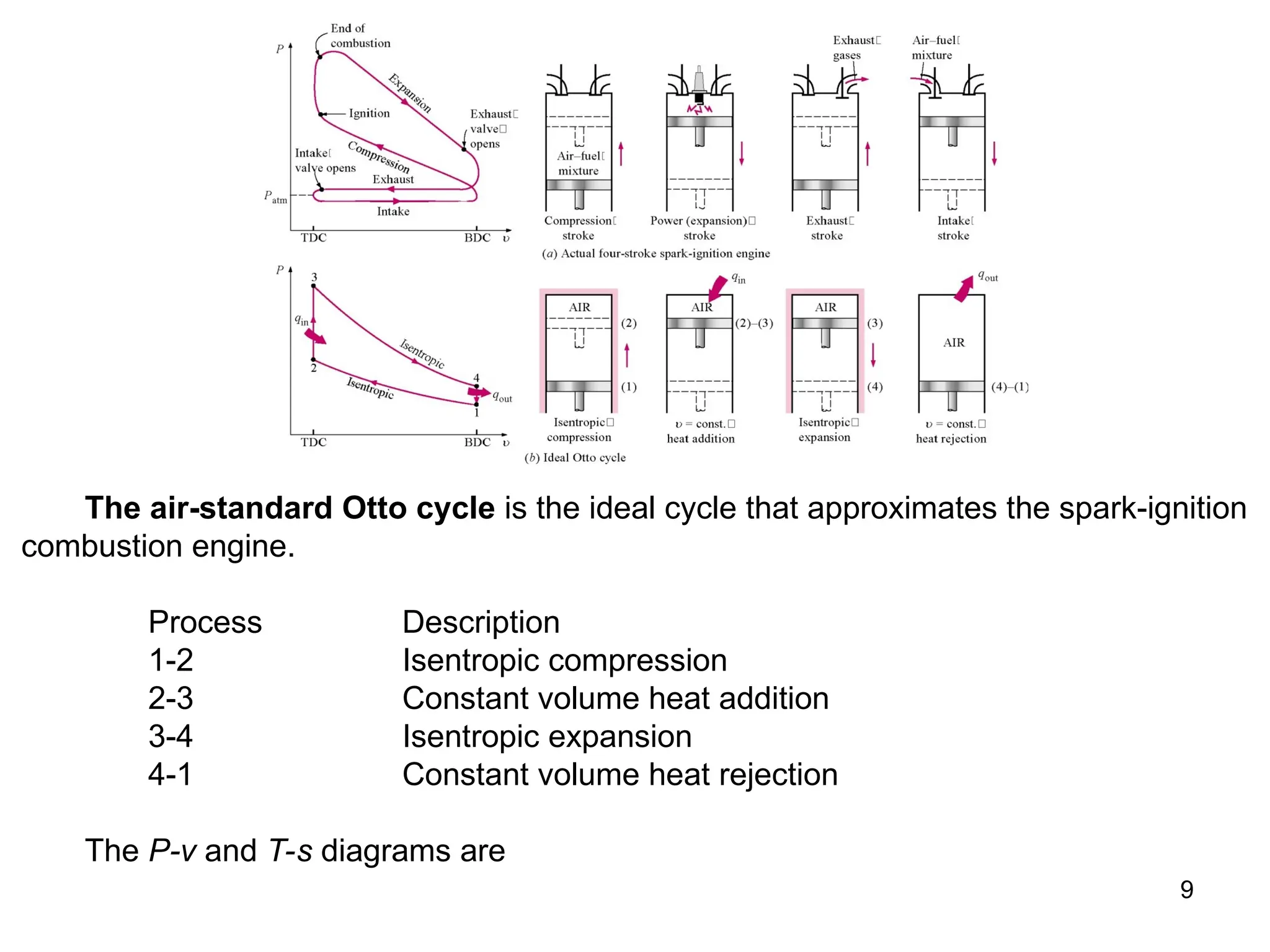
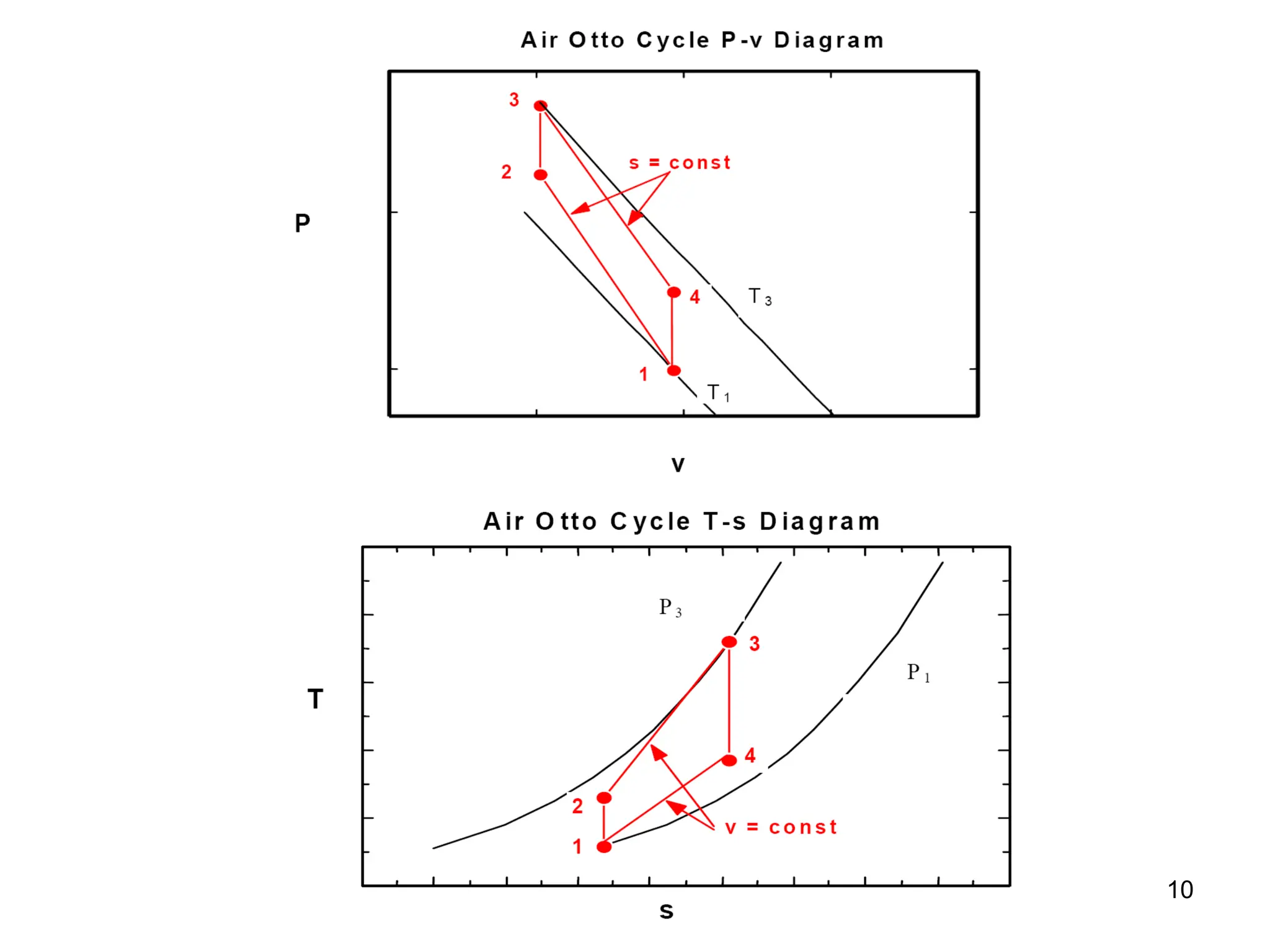
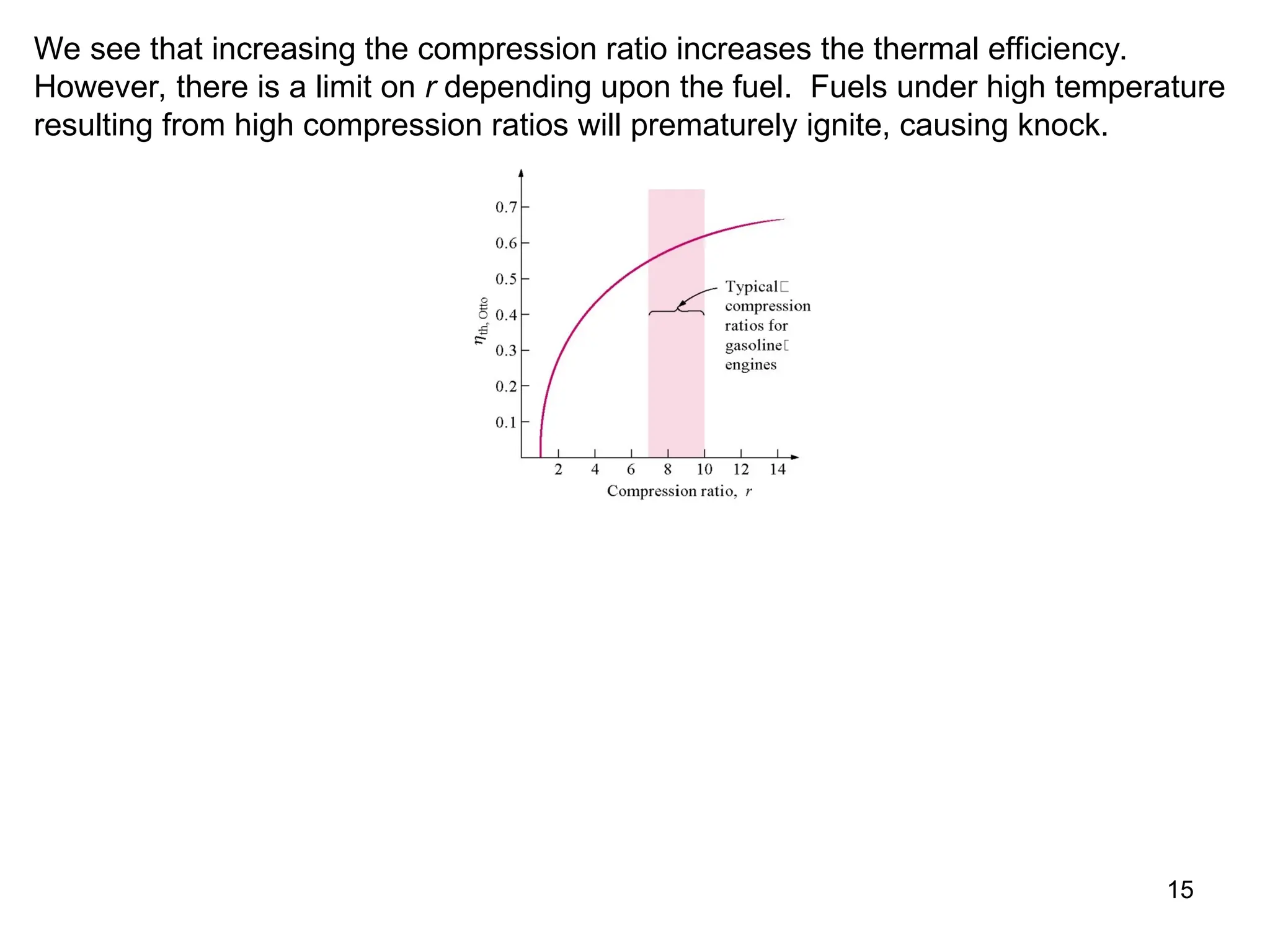
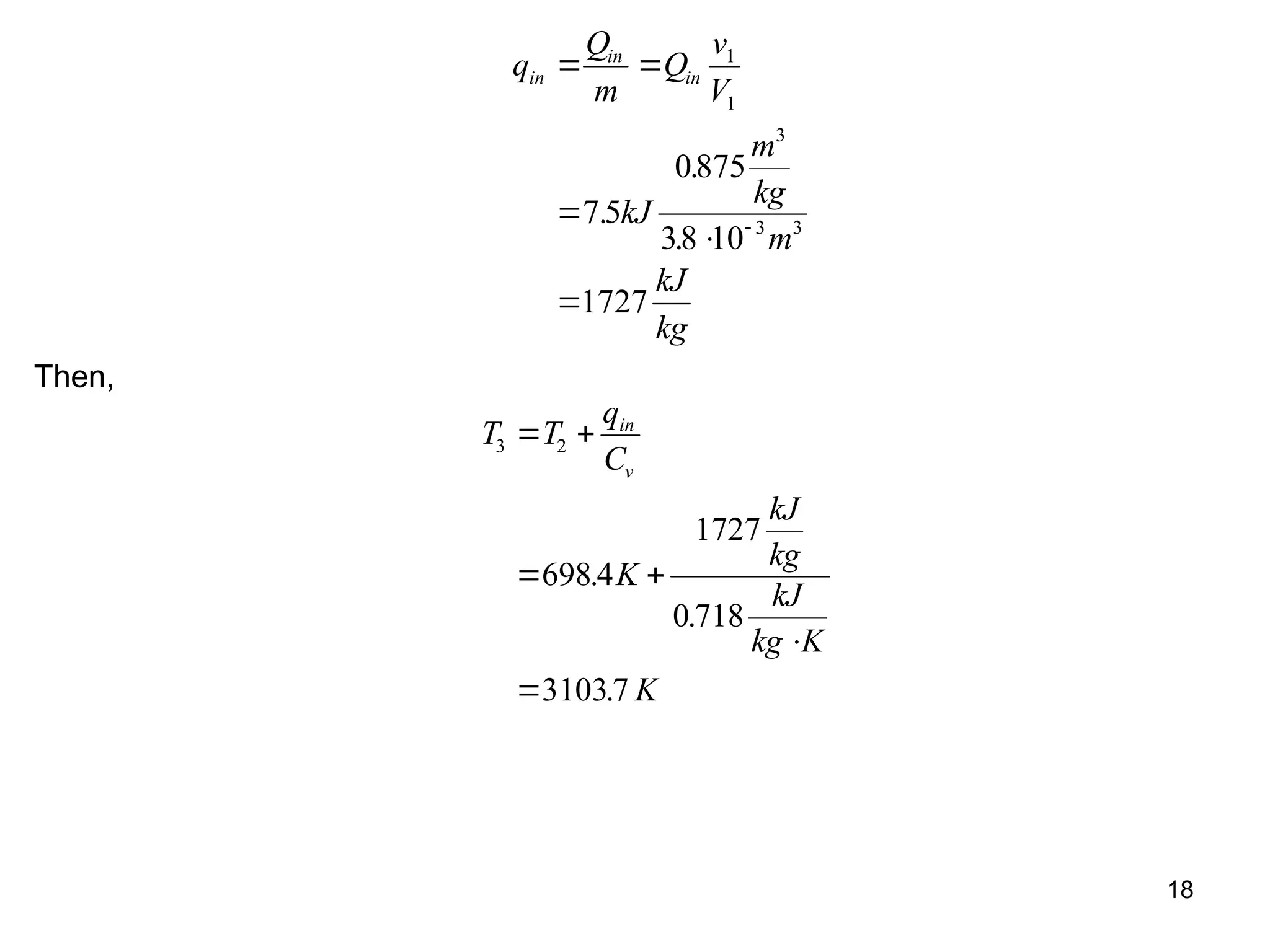
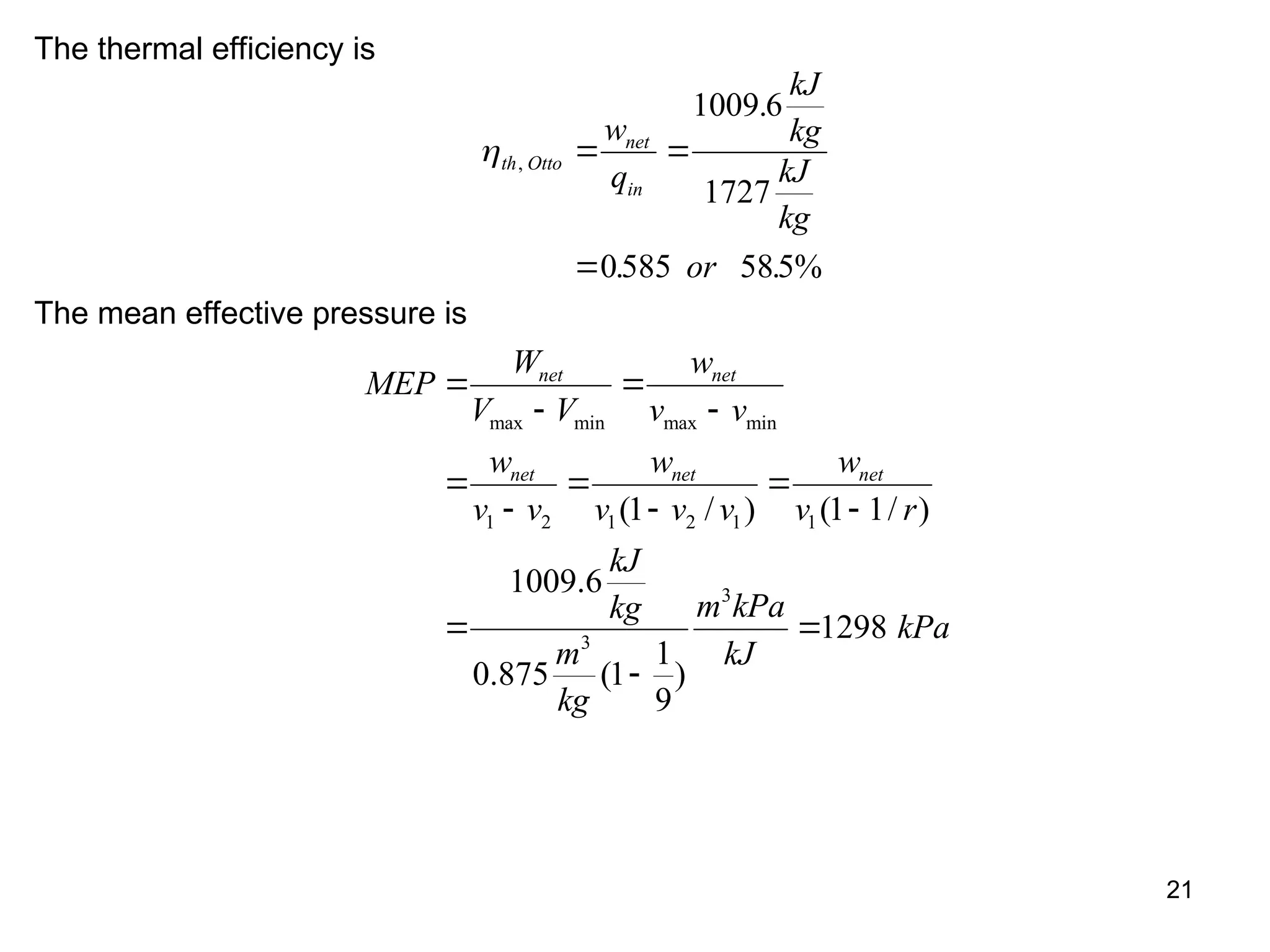
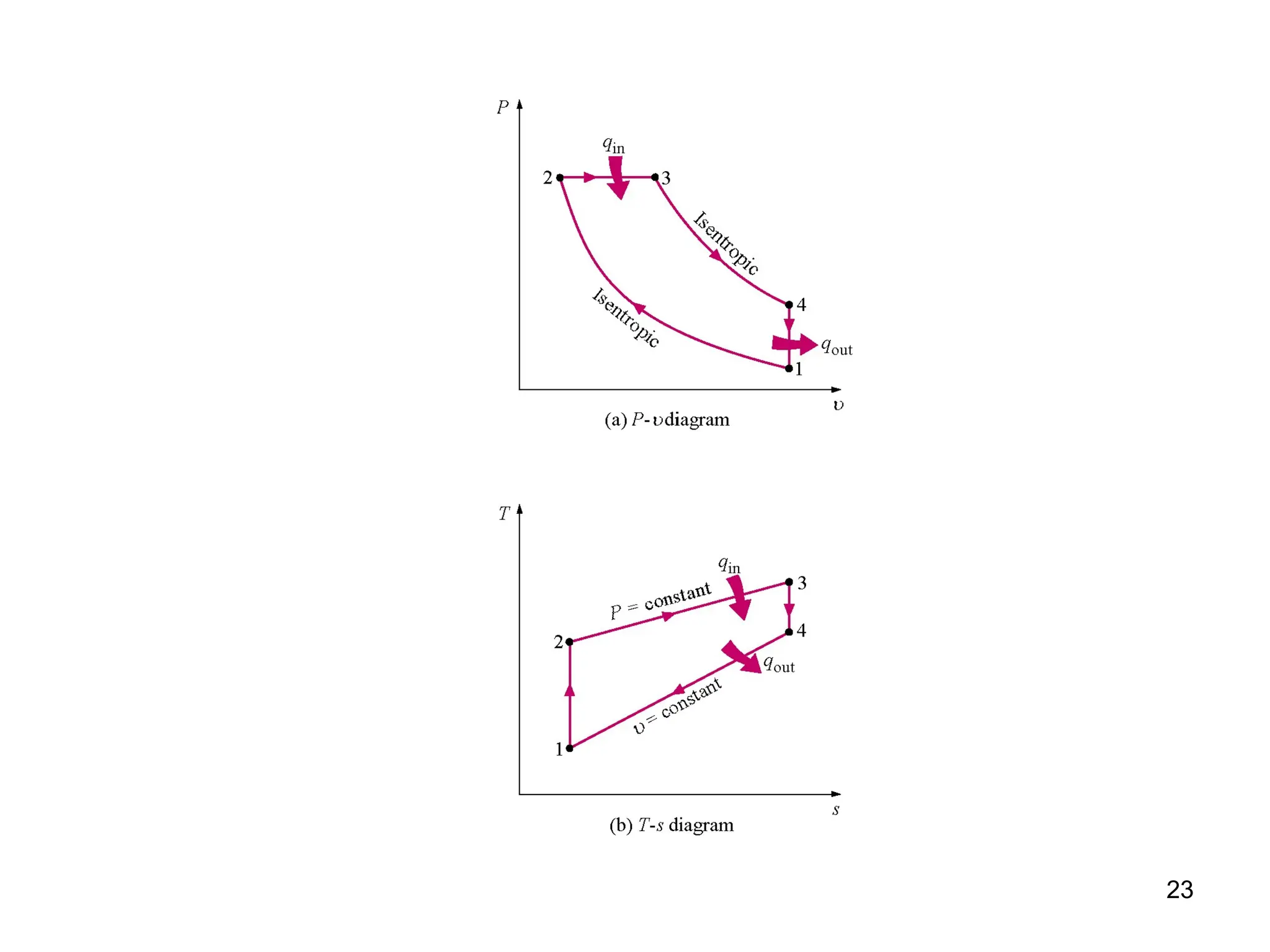
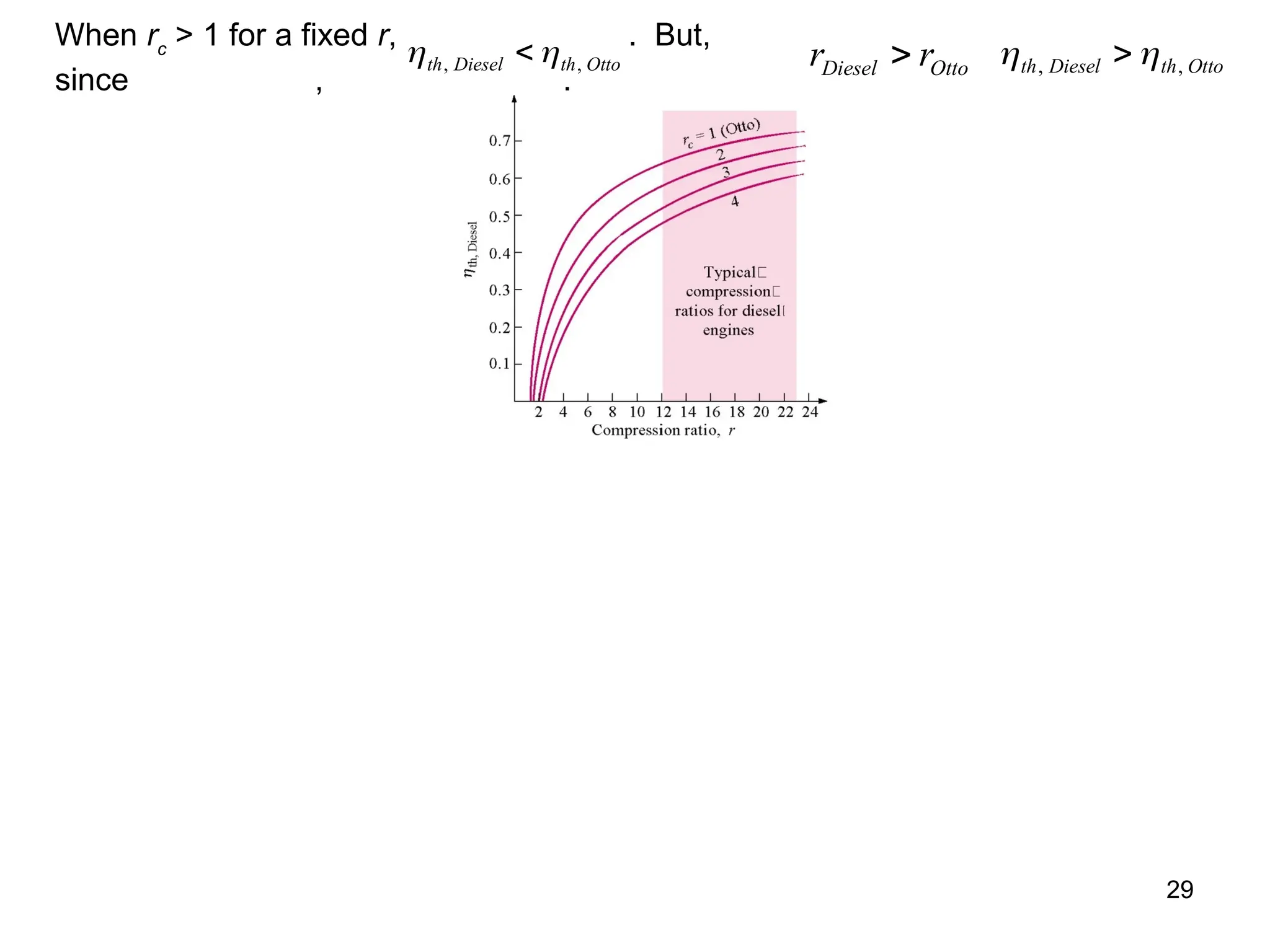
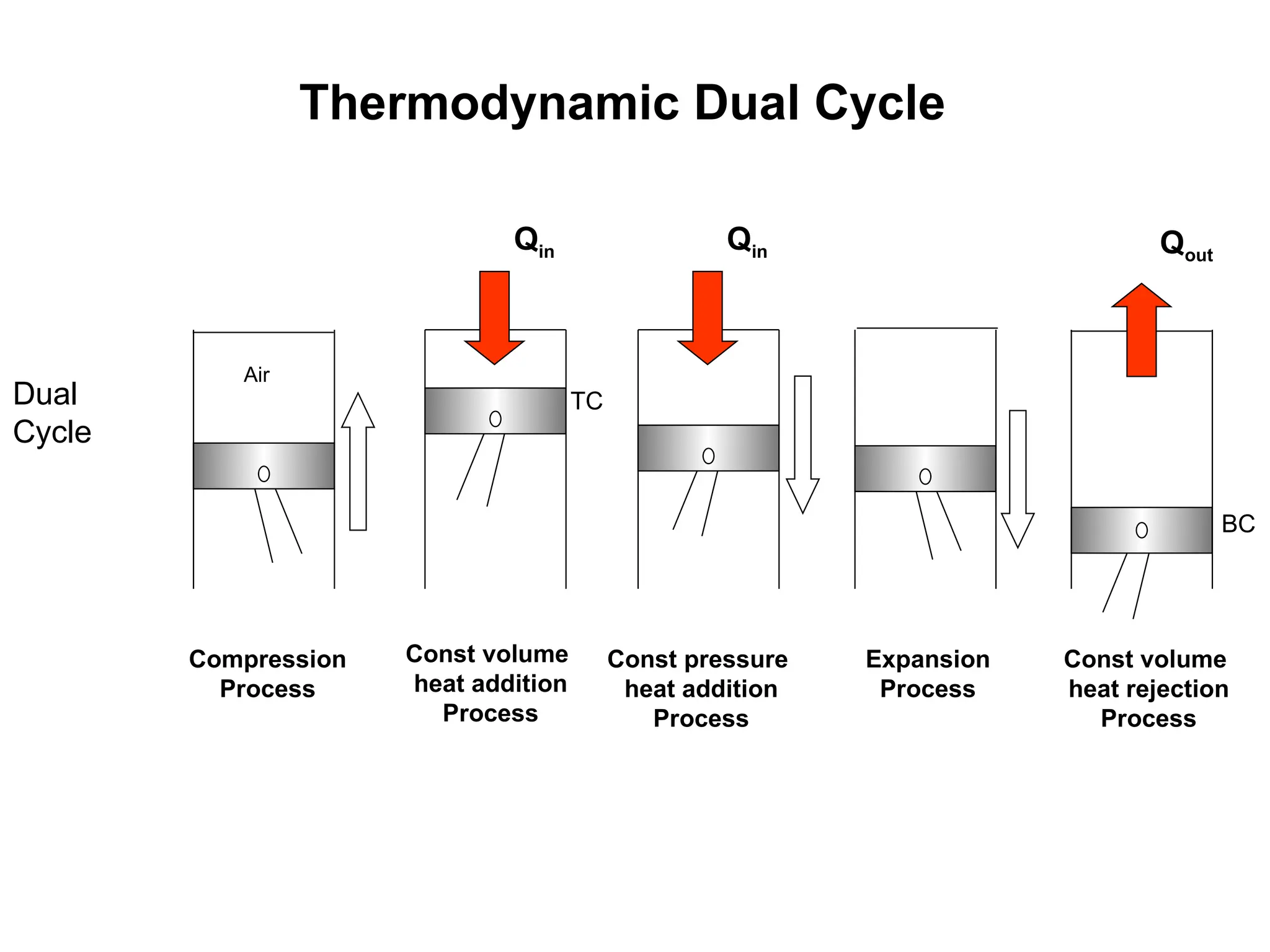
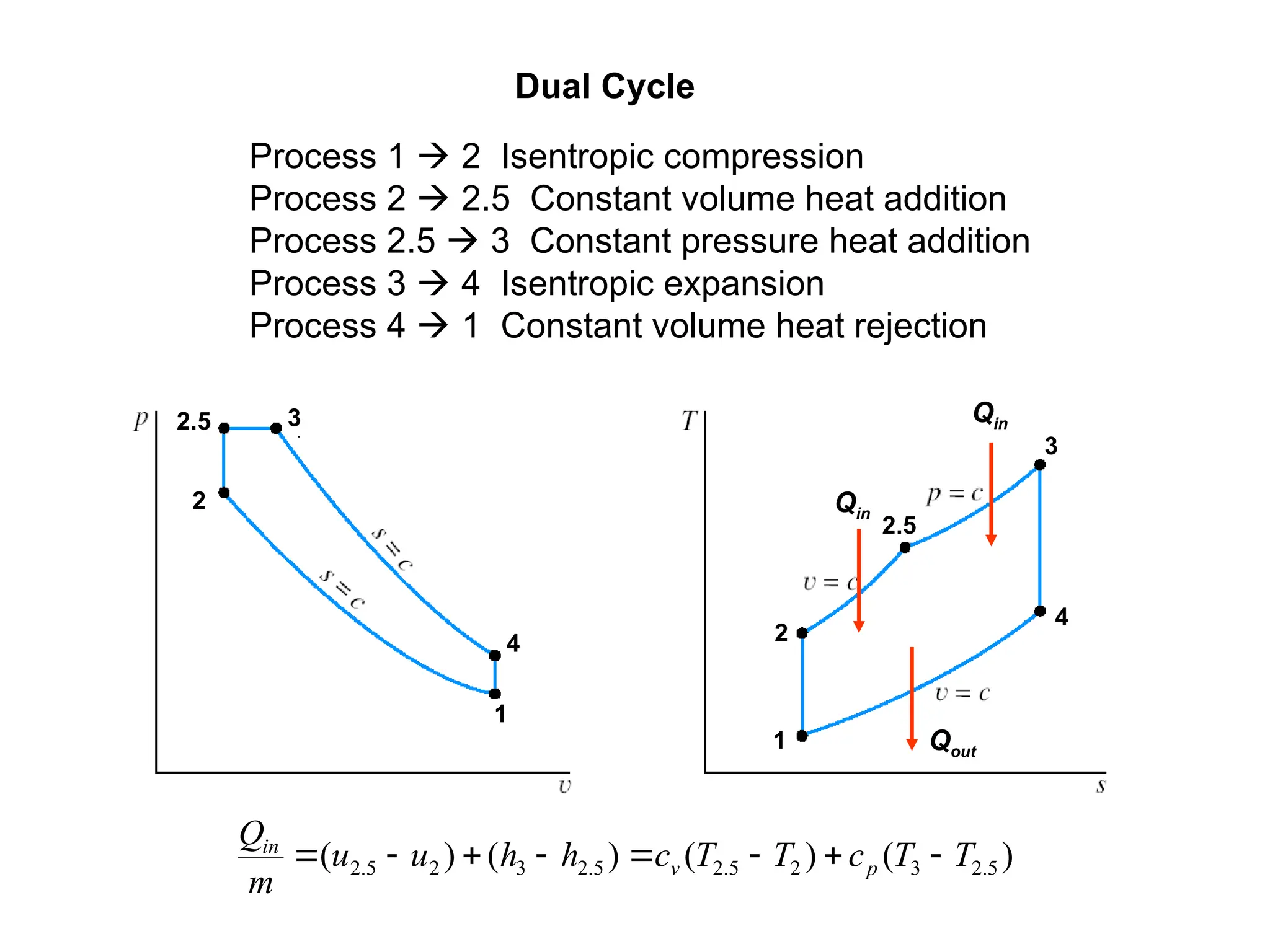
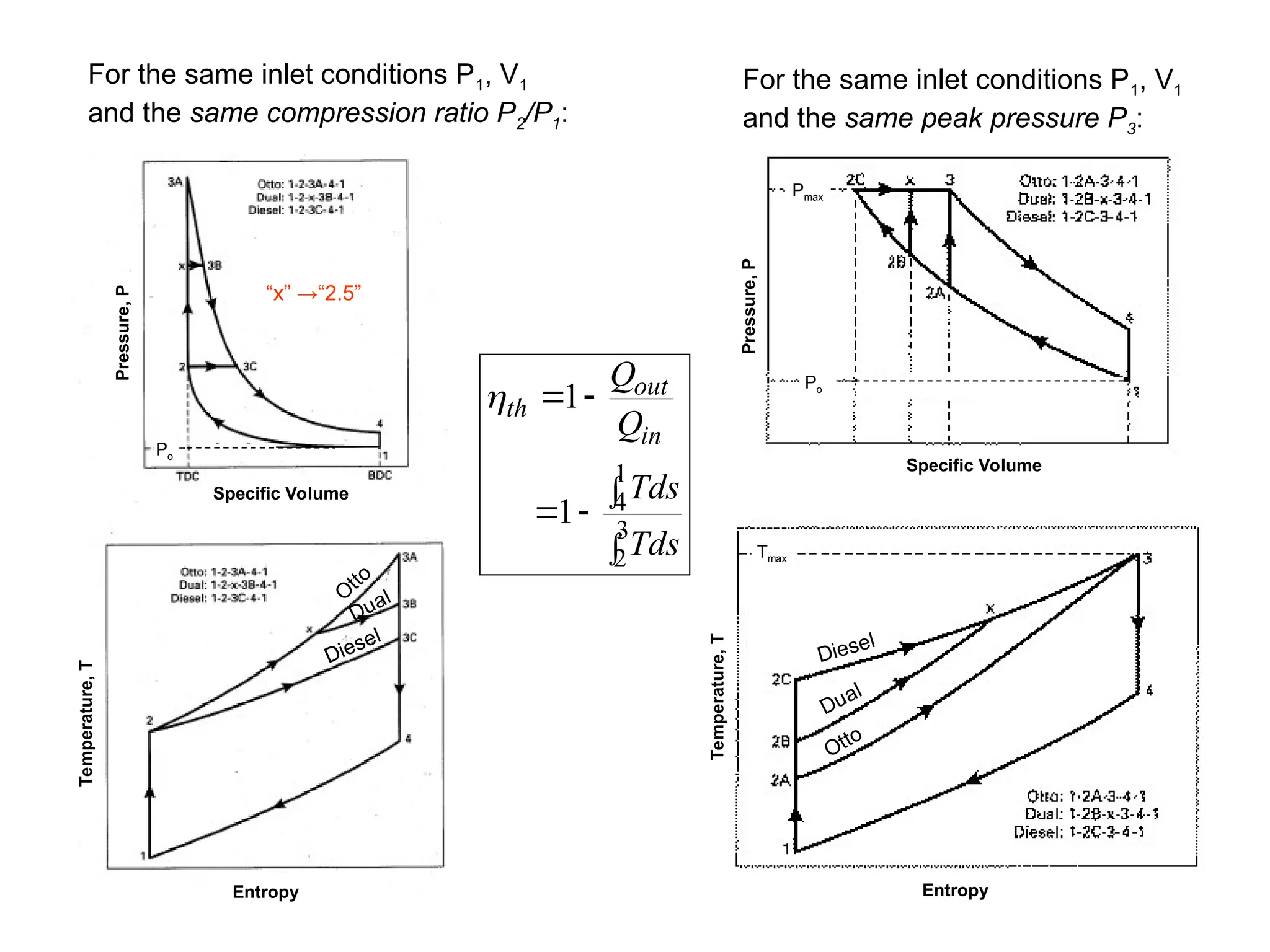
This document explores gas power cycles, focusing on ideal cycles like the Carnot and Otto cycles, detailing their processes and efficiency calculations. It emphasizes the assumptions made in modeling these cycles, such as treating air as an ideal gas and considering internally reversible processes. Additionally, it covers terms related to reciprocating engines and presents analysis on thermal efficiencies of both Otto and Diesel cycles.

1. UNIT 2
Gas Power Cycles
by
Deepa M S & Varuna Tandon
Source: Thermodynamics: An Engineering Approach, 5th
edition
by Yunus A. Çengel and Michael A. Boles

2. 2
Our study of gas power cycles will involve the study of those heat engines in which
the working fluid remains in the gaseous state throughout the cycle. We often study
the ideal cycle in which internal irreversibilities and complexities (the actual intake of
air and fuel, the actual combustion process, and the exhaust of products of
combustion among others) are removed.
We will be concerned with how the major parameters of the cycle affect the
performance of heat engines. The performance is often measured in terms of the
cycle efficiency.
th
net
in
W
Q


3. 3
Carnot Cycle
The Carnot cycle was introduced in Chapter 5 as the most efficient heat engine that
can operate between two fixed temperatures TH and TL. The Carnot cycle is
described by the following four processes.
Carnot Cycle
Process Description
1-2 Isothermal heat
addition
2-3 Isentropic expansion
3-4 Isothermal heat
rejection
4-1 Isentropic
compression

4. 4
Note the processes on both the P-v and T-s diagrams. The areas under the process
curves on the P-v diagram represent the work done for closed systems. The net
cycle work done is the area enclosed by the cycle on the P-v diagram. The areas
under the process curves on the T-s diagram represent the heat transfer for the
processes. The net heat added to the cycle is the area that is enclosed by the cycle
on the T-s diagram. For a cycle we know Wnet = Qnet; therefore, the areas enclosed
on the P-v and T-s diagrams are equal.
th Carnot
L
H
T
T
,  
1
We often use the Carnot efficiency as a means to think about ways to improve the
cycle efficiency of other cycles. One of the observations about the efficiency of both
ideal and actual cycles comes from the Carnot efficiency: Thermal efficiency
increases with an increase in the average temperature at which heat is supplied to
the system or with a decrease in the average temperature at which heat is rejected
from the system.

5. 5
Air-Standard Assumptions
In our study of gas power cycles, we assume that the working fluid is air, and the air
undergoes a thermodynamic cycle even though the working fluid in the actual power
system does not undergo a cycle.
To simplify the analysis, we approximate the cycles with the following assumptions:
•The air continuously circulates in a closed loop and always behaves as an ideal gas.
•All the processes that make up the cycle are internally reversible.
•The combustion process is replaced by a heat-addition process from an external
source.
•A heat rejection process that restores the working fluid to its initial state replaces the
exhaust process.
•The cold-air-standard assumptions apply when the working fluid is air and has
constant specific heat evaluated at room temperature (25o
C or 77o
F).

6. 6
Terminology for Reciprocating Devices
The following is some terminology we need to understand for reciprocating engines—
typically piston-cylinder devices. Let’s look at the following figures for the definitions
of top dead center (TDC), bottom dead center (BDC), stroke, bore, intake valve,
exhaust valve, clearance volume, displacement volume, compression ratio, and mean
effective pressure.

7. 7
The compression ratio r of an engine is the ratio of the maximum volume to the
minimum volume formed in the cylinder.
r
V
V
V
V
BDC
TDC
 
max
min
The mean effective pressure (MEP) is a fictitious pressure that, if it operated on the
piston during the entire power stroke, would produce the same amount of net work as
that produced during the actual cycle.
MEP
W
V V
w
v v
net net




max min max min

8. 8
Otto Cycle: The Ideal Cycle for Spark-Ignition Engines
Consider the automotive spark-ignition power cycle.
Processes
Intake stroke
Compression stroke
Power (expansion) stroke
Exhaust stroke
Often the ignition and combustion process begins before the completion of the
compression stroke. The number of crank angle degrees before the piston reaches
TDC on the number one piston at which the spark occurs is called the engine timing.
What are the compression ratio and timing of your engine in your car, truck, or
motorcycle?

9. 9
The air-standard Otto cycle is the ideal cycle that approximates the spark-ignition
combustion engine.
Process Description
1-2 Isentropic compression
2-3 Constant volume heat addition
3-4 Isentropic expansion
4-1 Constant volume heat rejection
The P-v and T-s diagrams are

10. 10

11. 11
Thermal Efficiency of the Otto cycle:
th
net
in
net
in
in out
in
out
in
W
Q
Q
Q
Q Q
Q
Q
Q
  

 
1
Now to find Qin
and Qout
.
Apply first law closed system to process 2-3, V = constant.
Thus, for constant specific heats,
Q U
Q Q mC T T
net
net in v
,
, ( )
23 23
23 3 2

  


12. 12
Apply first law closed system to process 4-1, V = constant.
Thus, for constant specific heats,
Q U
Q Q mC T T
Q mC T T mC T T
net
net out v
out v v
,
, ( )
( ) ( )
41 41
41 1 4
1 4 4 1

  
   

The thermal efficiency becomes
th Otto
out
in
v
v
Q
Q
mC T T
mC T T
,
( )
( )
 
 


1
1 4 1
3 2

13. 13
th Otto
T T
T T
T T T
T T T
,
( )
( )
( / )
( / )
 


 


1
1
1
1
4 1
3 2
1 4 1
2 3 2
Recall processes 1-2 and 3-4 are isentropic, so
Since V3 = V2 and V4 = V1, we see that
T
T
T
T
or
T
T
T
T
2
1
3
4
4
1
3
2



14. 14
The Otto cycle efficiency becomes
th Otto
T
T
,  
1 1
2
Is this the same as the Carnot cycle efficiency?
Since process 1-2 is isentropic,
where the compression ratio is r = V1/V2 and
th Otto k
r
,   
1
1
1

15. 15
We see that increasing the compression ratio increases the thermal efficiency.
However, there is a limit on r depending upon the fuel. Fuels under high temperature
resulting from high compression ratios will prematurely ignite, causing knock.

16. 16
Example 9-1
An Otto cycle having a compression ratio of 9:1 uses air as the working fluid. Initially
P1 = 95 kPa, T1 = 17o
C, and V1 = 3.8 liters. During the heat addition process, 7.5 kJ
of heat are added. Determine all T's, P's, th, the back work ratio, and the mean
effective pressure.
Process Diagrams: Review the P-v and T-s diagrams given above for the Otto
cycle.
Assume constant specific heats with Cv = 0.718 kJ/kg K, k = 1.4. (Use the 300 K
data from Table A-2)
Process 1-2 is isentropic; therefore, recalling that r = V1/V2 = 9,

17. 17
The first law closed system for process 2-3 was shown to reduce to (your homework
solutions must be complete; that is, develop your equations from the application of
the first law for each process as we did in obtaining the Otto cycle efficiency equation)
Q mC T T
in v
 
( )
3 2
Let qin = Qin / m and m = V1/v1
v
RT
P
kJ
kg K
K
kPa
m kPa
kJ
m
kg
1
1
1
3
3
0 287 290
95
0875




. ( )
.

18. 18
q
Q
m
Q
v
V
kJ
m
kg
m
kJ
kg
in
in
in
 




1
1
3
3 3
7 5
0875
38 10
1727
.
.
.
Then,
T T
q
C
K
kJ
kg
kJ
kg K
K
in
v
3 2
698 4
1727
0 718
31037
 
 


.
.
.

19. 19
Using the combined gas law (V3 = V2)
P P
T
T
MPa
3 2
3
2
915
  .
Process 3-4 is isentropic; therefore,
1 1 1.4 1
3
4 3 3
4
1 1
(3103.7)
9
1288.8
k k
V
T T T K
V r
K
  
     
  
     
   
 


20. 20
Process 4-1 is constant volume. So the first law for the closed system gives, on a
mass basis,
Q mC T T
q
Q
m
C T T
kJ
kg K
K
kJ
kg
out v
out
out
v
 
  




( )
( )
. ( . )
.
4 1
4 1
0 718 12888 290
7171
The first law applied to the cycle gives (Recall ucycle = 0)
w q q q
kJ
kg
kJ
kg
net net in out
  
 

( . )
.
1727 717 4
1009 6

21. 21
The thermal efficiency is
th Otto
net
in
w
q
kJ
kg
kJ
kg
or
,
.
. .
 

1009 6
1727
0585 585%
The mean effective pressure is
max min max min
1 2 1 2 1 1
3
3
(1 / ) (1 1/ )
1009.6
1298
1
0.875 (1 )
9
net net
net net net
W w
MEP
V V v v
w w w
v v v v v v r
kJ
m kPa
kg
kPa
m kJ
kg
 
 
  
  
 


22. 22
The back work ratio is (can you show that this is true?)
2 1
12 2 1
exp 34 3 4 3 4
( ) ( )
( ) ( )
0.225 22.5%
comp v
v
w C T T
u T T
BWR
w u C T T T T
or

 
   
   

Air-Standard Diesel Cycle
The air-standard Diesel cycle is the ideal cycle that approximates the Diesel
combustion engine
Process Description
1-2 Isentropic compression
2-3 Constant pressure heat addition
3-4 Isentropic expansion
4-1 Constant volume heat rejection
The P-v and T-s diagrams are

23. 23

24. 24
Thermal efficiency of the Diesel cycle
th Diesel
net
in
out
in
W
Q
Q
Q
,   
1
Now to find Qin and Qout.
Apply the first law closed system to process 2-3, P = constant.
Thus, for constant specific heats
Q U P V V
Q Q mC T T mR T T
Q mC T T
net
net in v
in p
,
,
( )
( ) ( )
( )
23 23 2 3 2
23 3 2 3 2
3 2
  
    
 


25. 25
Apply the first law closed system to process 4-1, V = constant (just as we did for the
Otto cycle)
Thus, for constant specific heats
Q U
Q Q mC T T
Q mC T T mC T T
net
net out v
out v v
,
, ( )
( ) ( )
41 41
41 1 4
1 4 4 1

  
   

The thermal efficiency becomes
th Diesel
out
in
v
p
Q
Q
mC T T
mC T T
,
( )
( )
 
 


1
1 4 1
3 2

26. 26
th Diesel
v
p
C T T
C T T
k
T T T
T T T
,
( )
( )
( / )
( / )
 


 


1
1
1 1
1
4 1
3 2
1 4 1
2 3 2
What is T3/T2 ?
PV
T
PV
T
P P
T
T
V
V
rc
3 3
3
2 2
2
3 2
3
2
3
2
 
 
where
where rc is called the cutoff ratio, defined as V3 /V2, and is a measure of the duration
of the heat addition at constant pressure. Since the fuel is injected directly into the
cylinder, the cutoff ratio can be related to the number of degrees that the crank
rotated during the fuel injection into the cylinder.

27. 27
What is T4/T1 ?
PV
T
PV
T
V V
T
T
P
P
4 4
4
1 1
1
4 1
4
1
4
1
 

where
Recall processes 1-2 and 3-4 are isentropic, so
PV PV PV PV
k k k k
1 1 2 2 4 4 3 3
 
and
Since V4 = V1 and P3 = P2, we divide the second equation by the first equation and
obtain
Therefore,

28. 28
th Diesel
c
k
c
k
c
k
c
k
T T T
T T T
k
T
T
r
r
r
r
k r
,
( / )
( / )
( )
( )
 


 


 



1
1 1
1
1
1 1
1
1
1 1
1
1 4 1
2 3 2
1
2
1
* What happens as rc goes to 1? Sketch the P-v diagram for the Diesel cycle and
show rc approaching 1 in the limit.

29. 29
 
th Diesel th Otto
, ,
 r r
Diesel Otto
  
th Diesel th Otto
, ,

When rc
> 1 for a fixed r, . But,
since , .

30. Air
TC
BC
Qin Qout
Compression
Process
Const pressure
heat addition
Process
Expansion
Process
Const volume
heat rejection
Process
Dual
Cycle
Qin
Const volume
heat addition
Process
Thermodynamic Dual Cycle

31. Process 1  2 Isentropic compression
Process 2  2.5 Constant volume heat addition
Process 2.5  3 Constant pressure heat addition
Process 3  4 Isentropic expansion
Process 4  1 Constant volume heat rejection
Dual Cycle
Qin
Qin
Qout
1
1
2
2
2.5
2.5
3
3
4
4
)
(
)
(
)
(
)
( 5
.
2
3
2
5
.
2
5
.
2
3
2
5
.
2 T
T
c
T
T
c
h
h
u
u
m
Q
p
v
in









32. Thermal Efficiency
)
(
)
(
1
1
5
.
2
3
2
5
.
2
1
4
h
h
u
u
u
u
m
Q
m
Q
in
out
cycle
Dual









 










 
1
)
1
(
1
1
1 1
c
k
c
k
c
const
Dual
r
k
r
r
v 



1
1
1 

 k
Otto
r

 
 









 
1
1
1
1
1 1
c
k
c
k
const c
Diesel
r
r
k
r
V

Note, the Otto cycle (rc=1) and the Diesel cycle (=1) are special cases:
2
3
5
.
2
3 and
where
P
P
v
v
rc 
 

33. The use of the Dual cycle requires information about either:
i) the fractions of constant volume and constant pressure heat addition
(common assumption is to equally split the heat addition), or
ii) maximum pressure P3.
Transformation of rc and  into more natural variables yields



















  1
1
1
1
1 1
1
1 k
r
V
P
Q
k
k
r k
in
c


1
3
1
P
P
rk


For the same inlet conditions P1, V1 and the same compression ratio:
Diesel
Dual
Otto 

 

For the same inlet conditions P1, V1 and the same peak pressure P3
(actual design limitation in engines):
otto
Dual
Diesel 

 


34. For the same inlet conditions P1, V1
and the same compression ratio P2/P1:
For the same inlet conditions P1, V1
and the same peak pressure P3:






3
2
1
4
1
1
Tds
Tds
Q
Q
in
out
th

Diesel
Dual
Otto
Diesel
Dual
O
tto
“x” →“2.5”
Pmax
Tmax
Po
Po
Pressure,
P
Pressure,
P
Temperature,
T
Temperature,
T
Specific Volume
Specific Volume
Entropy Entropy