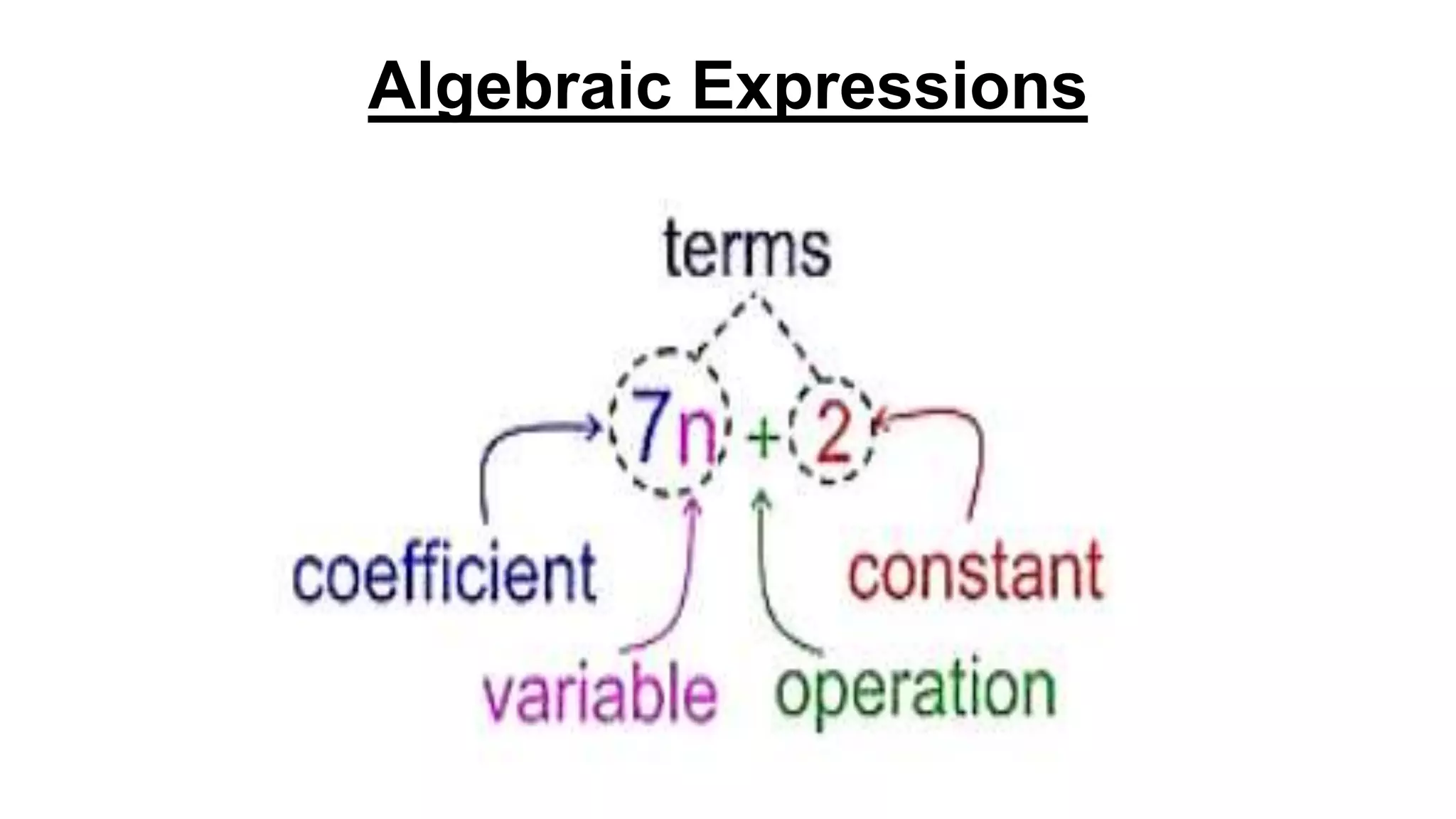
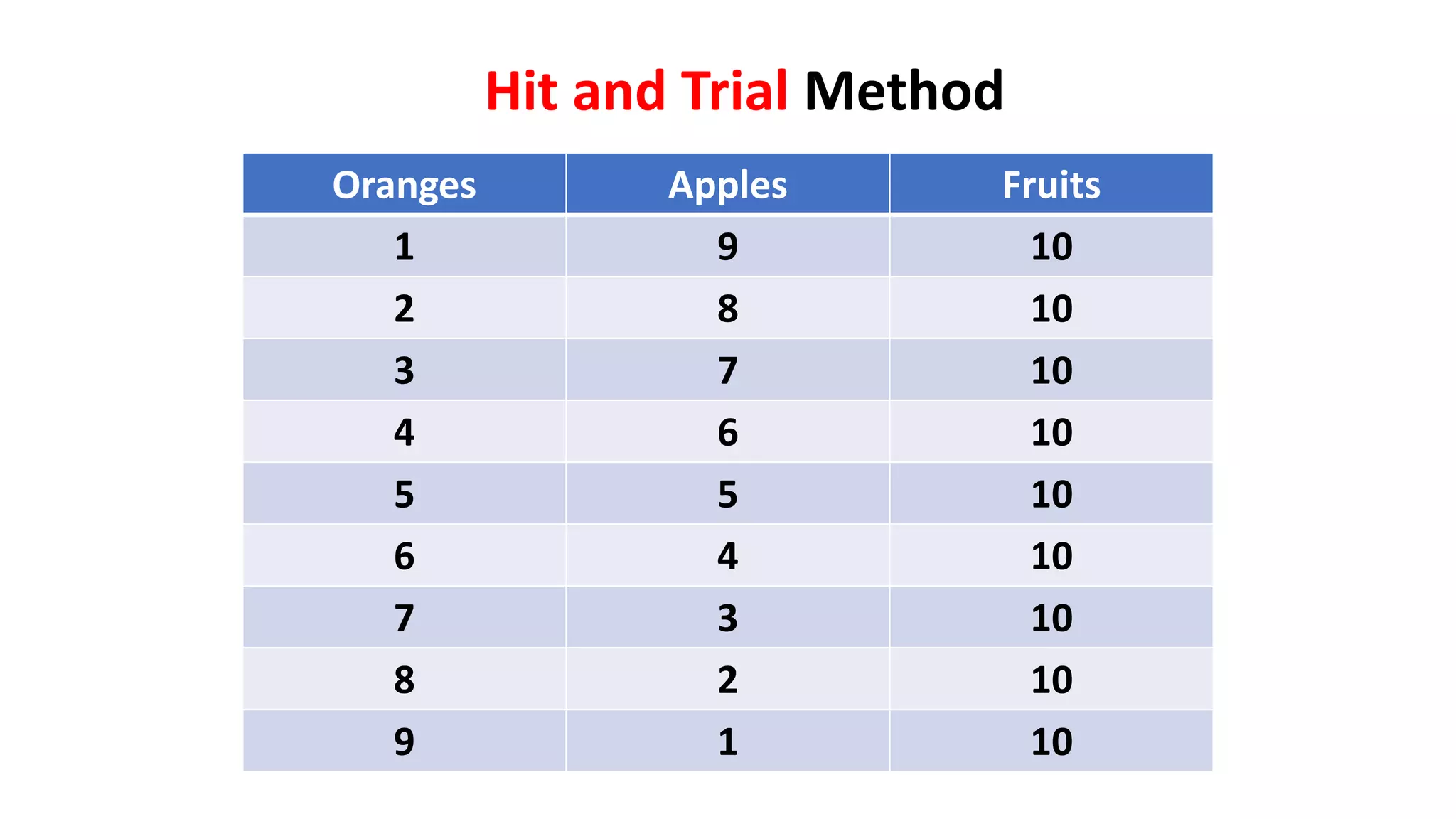
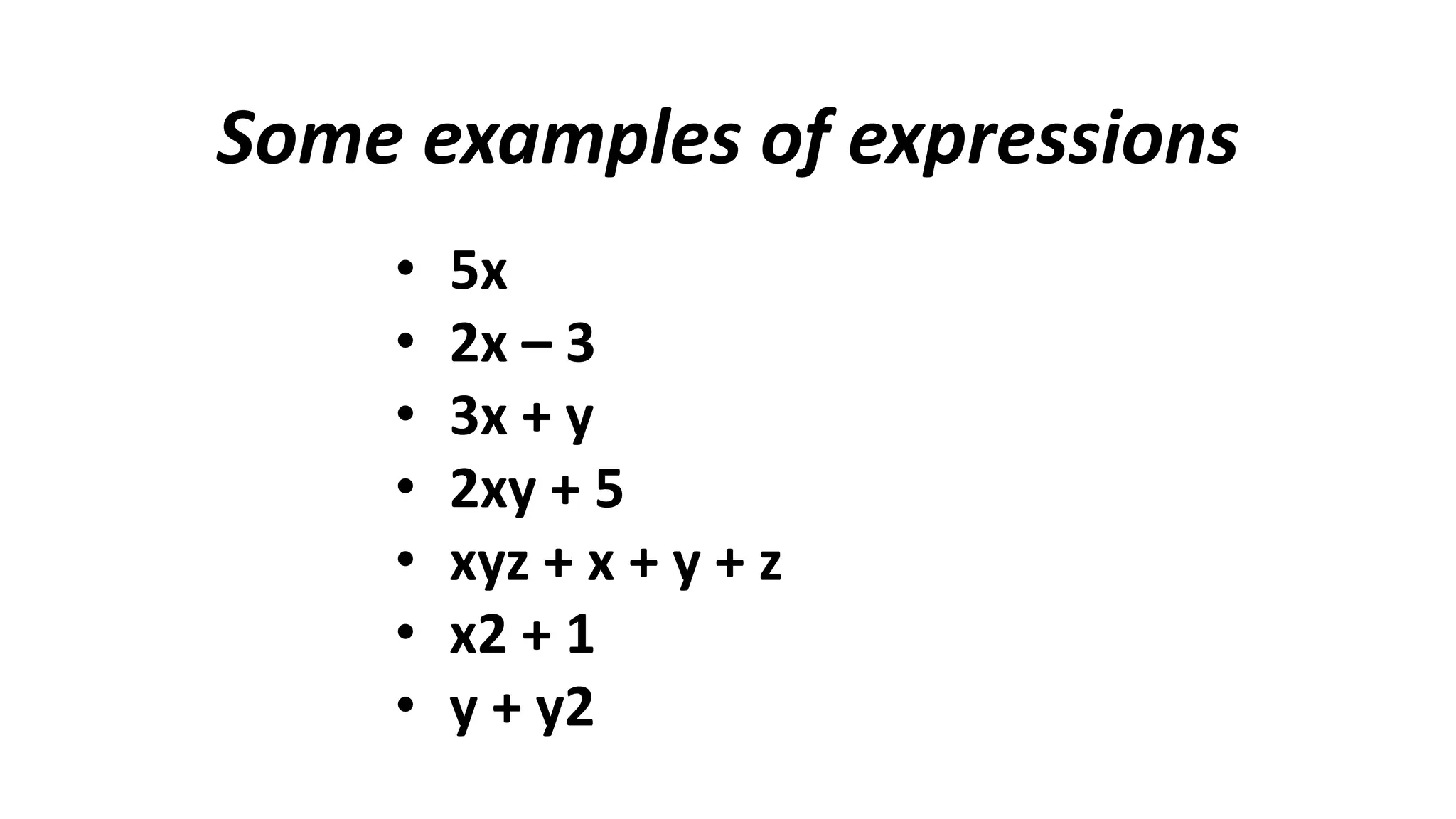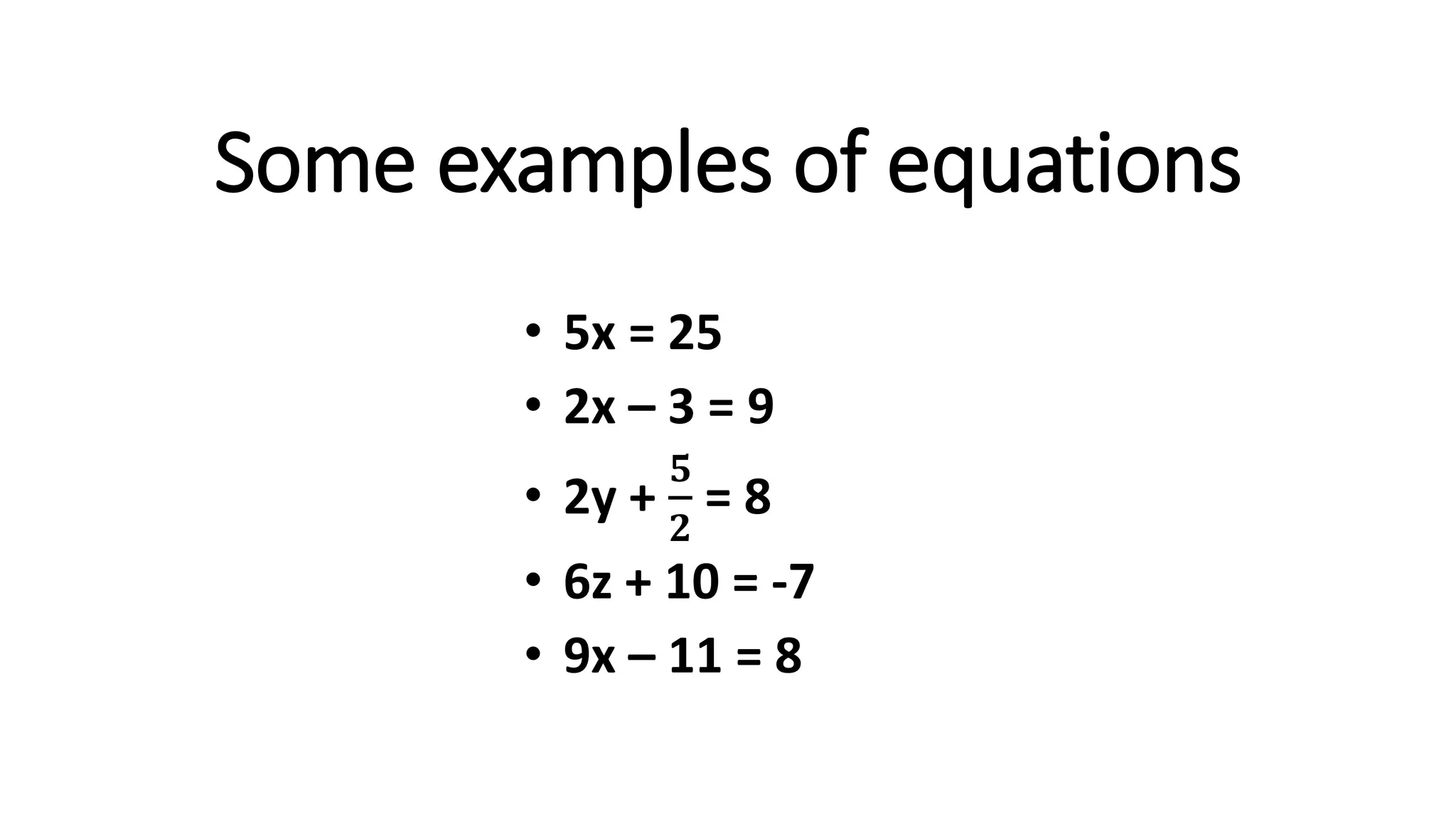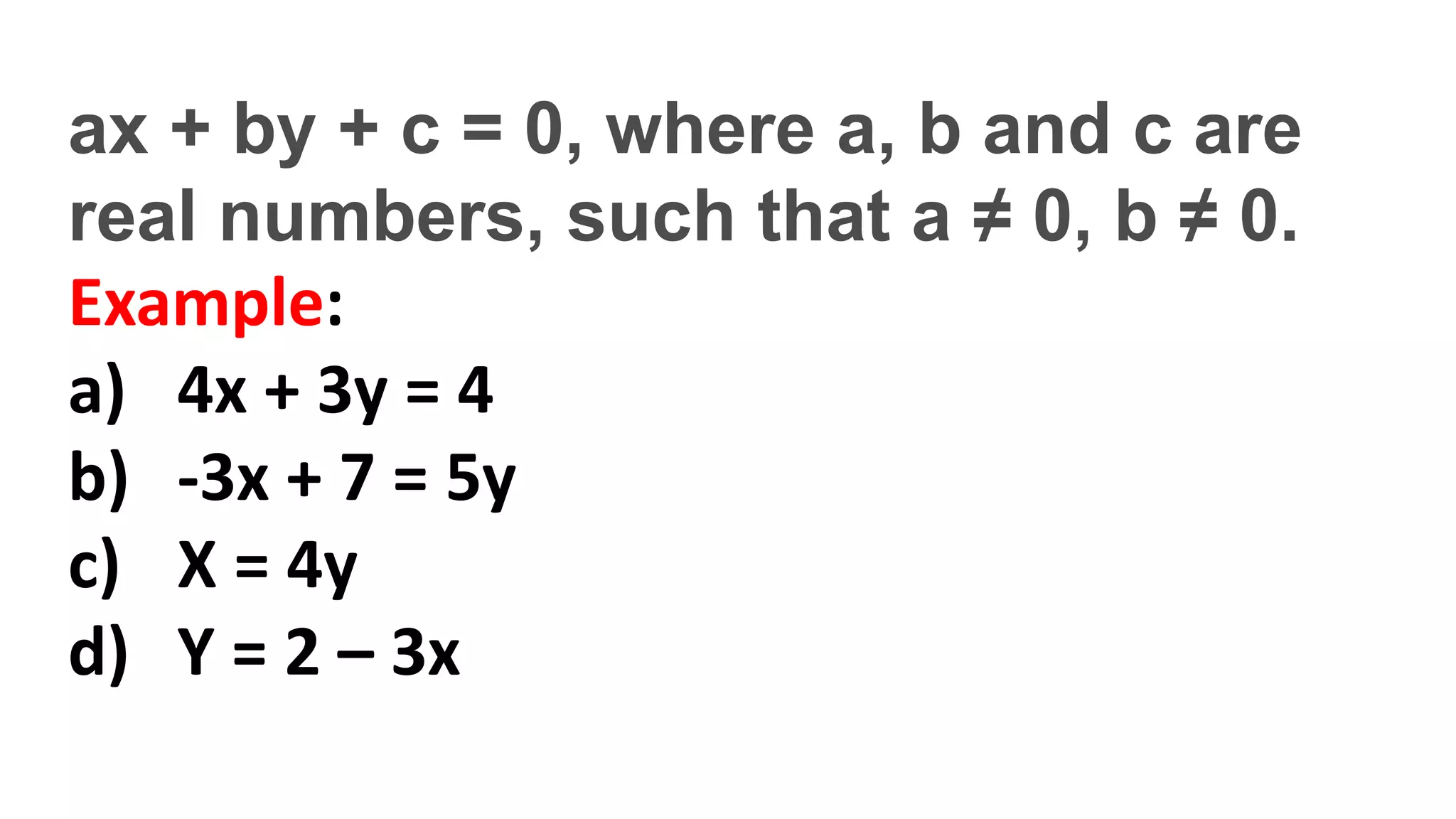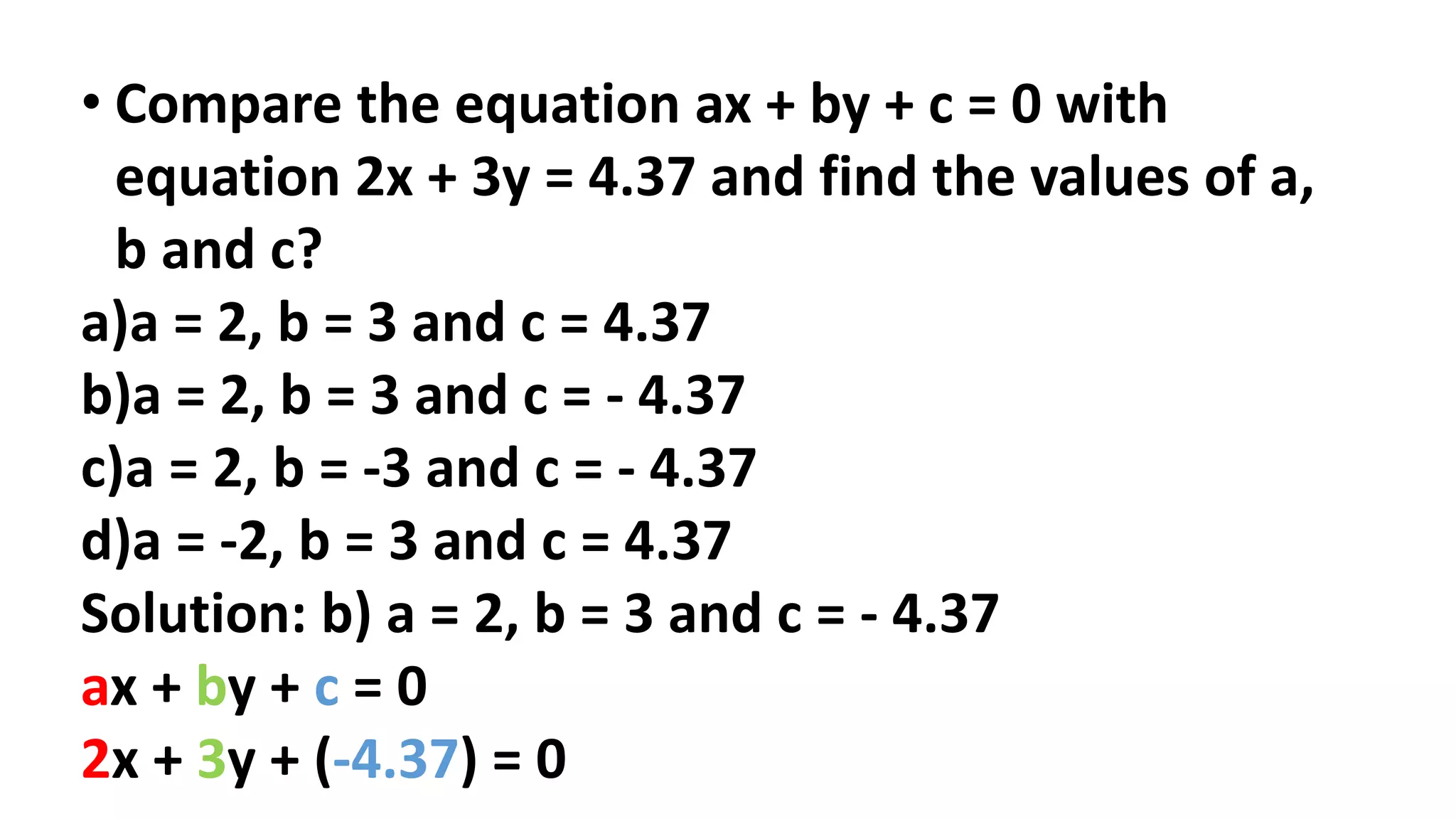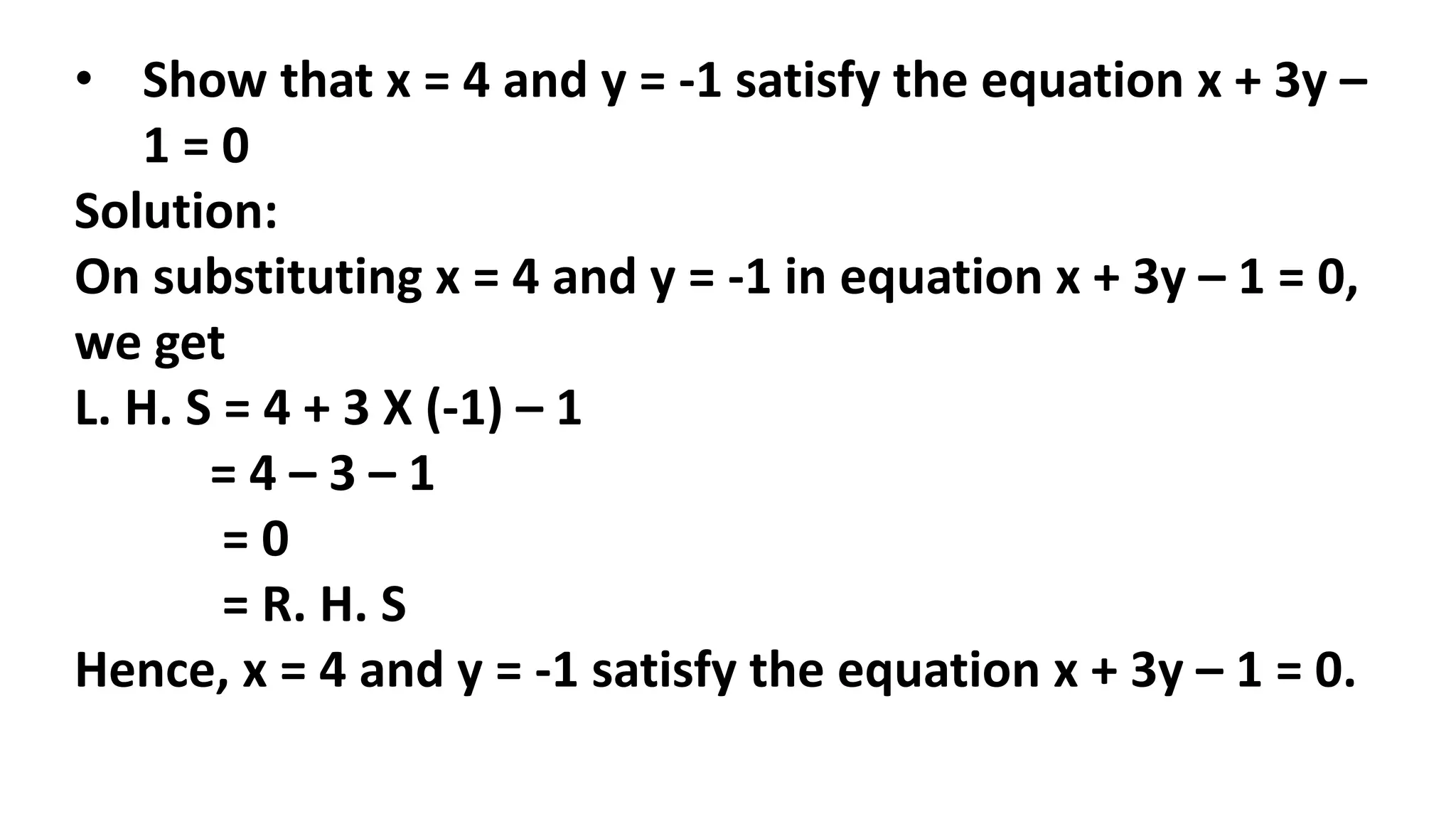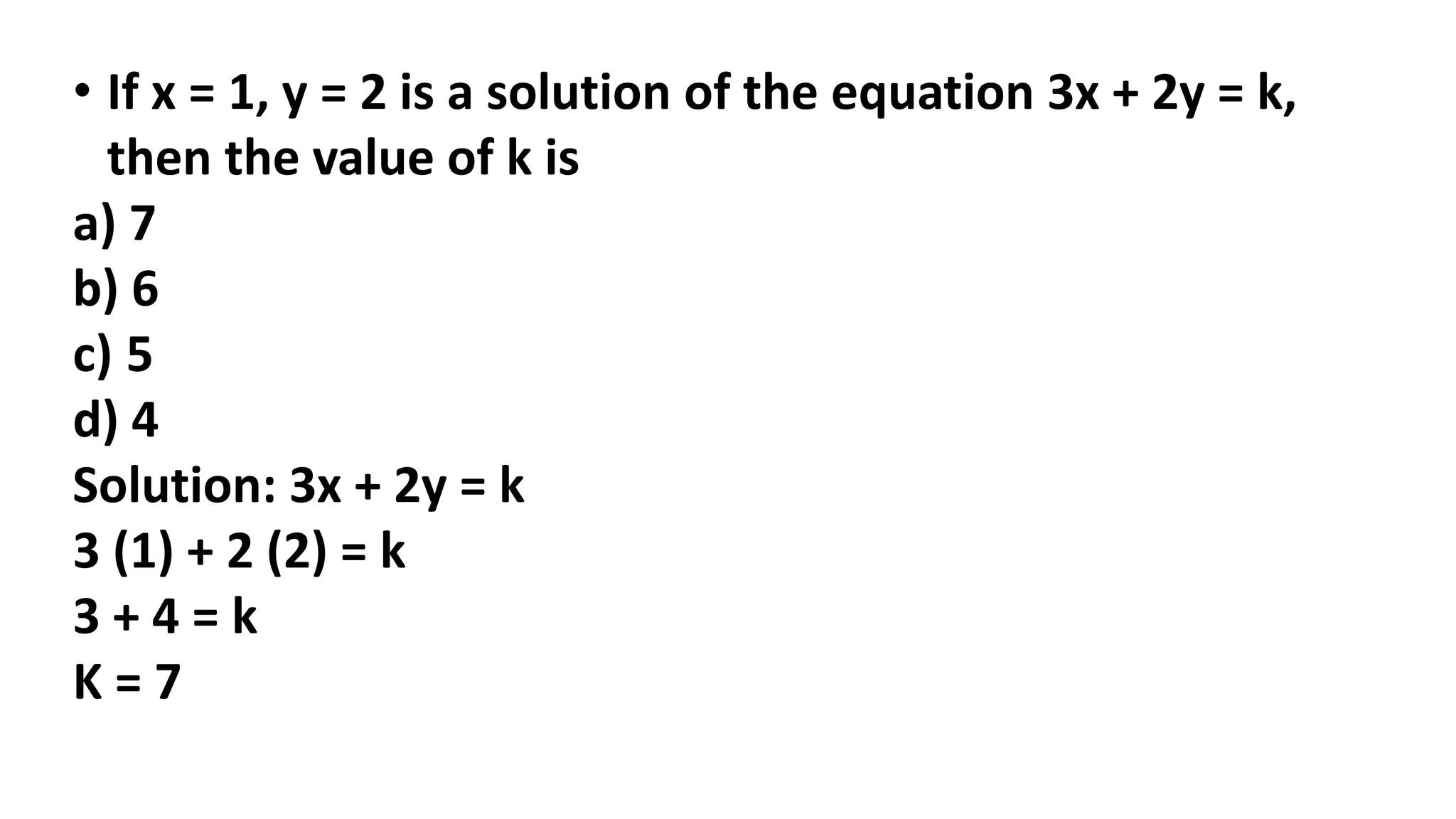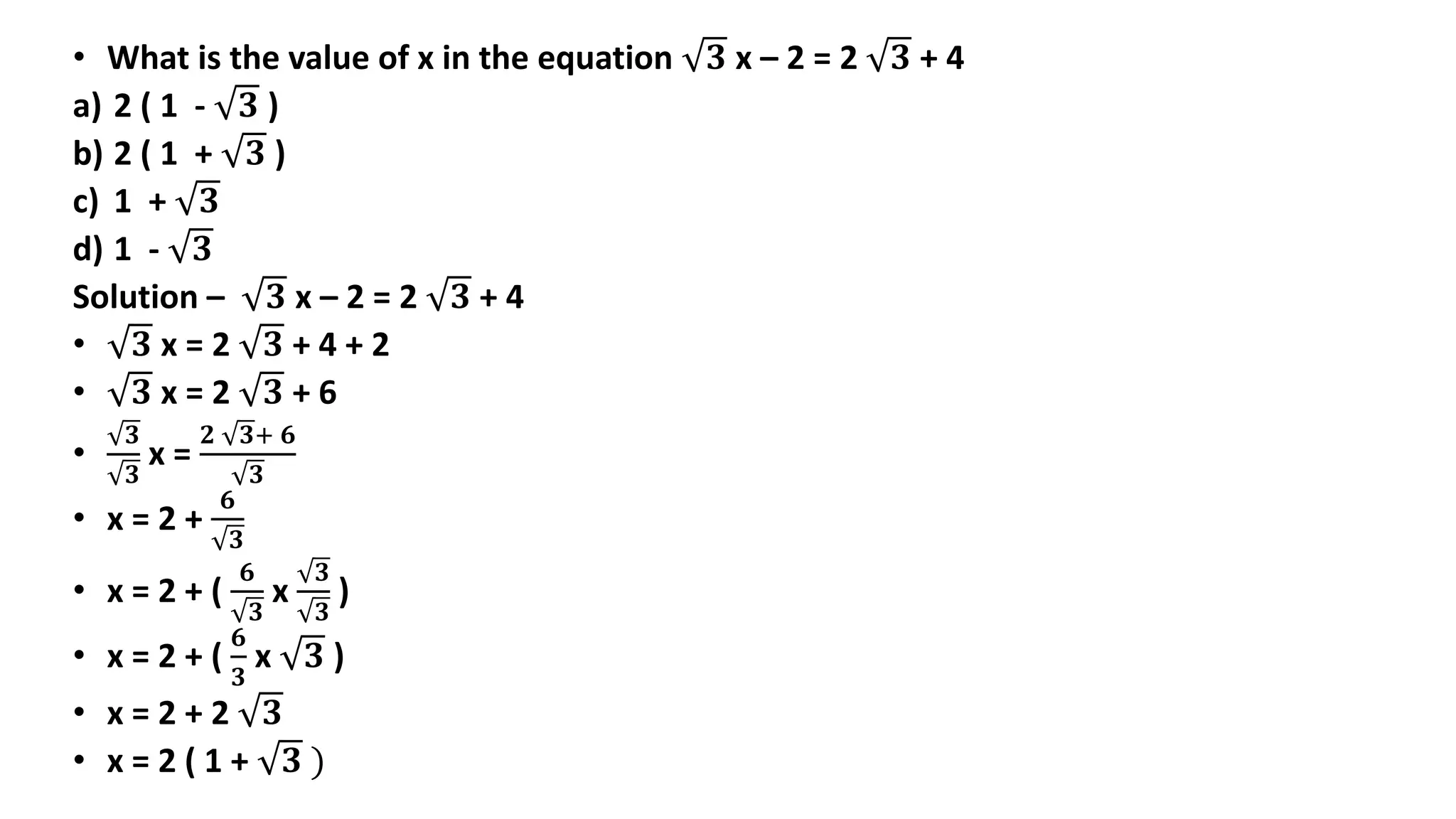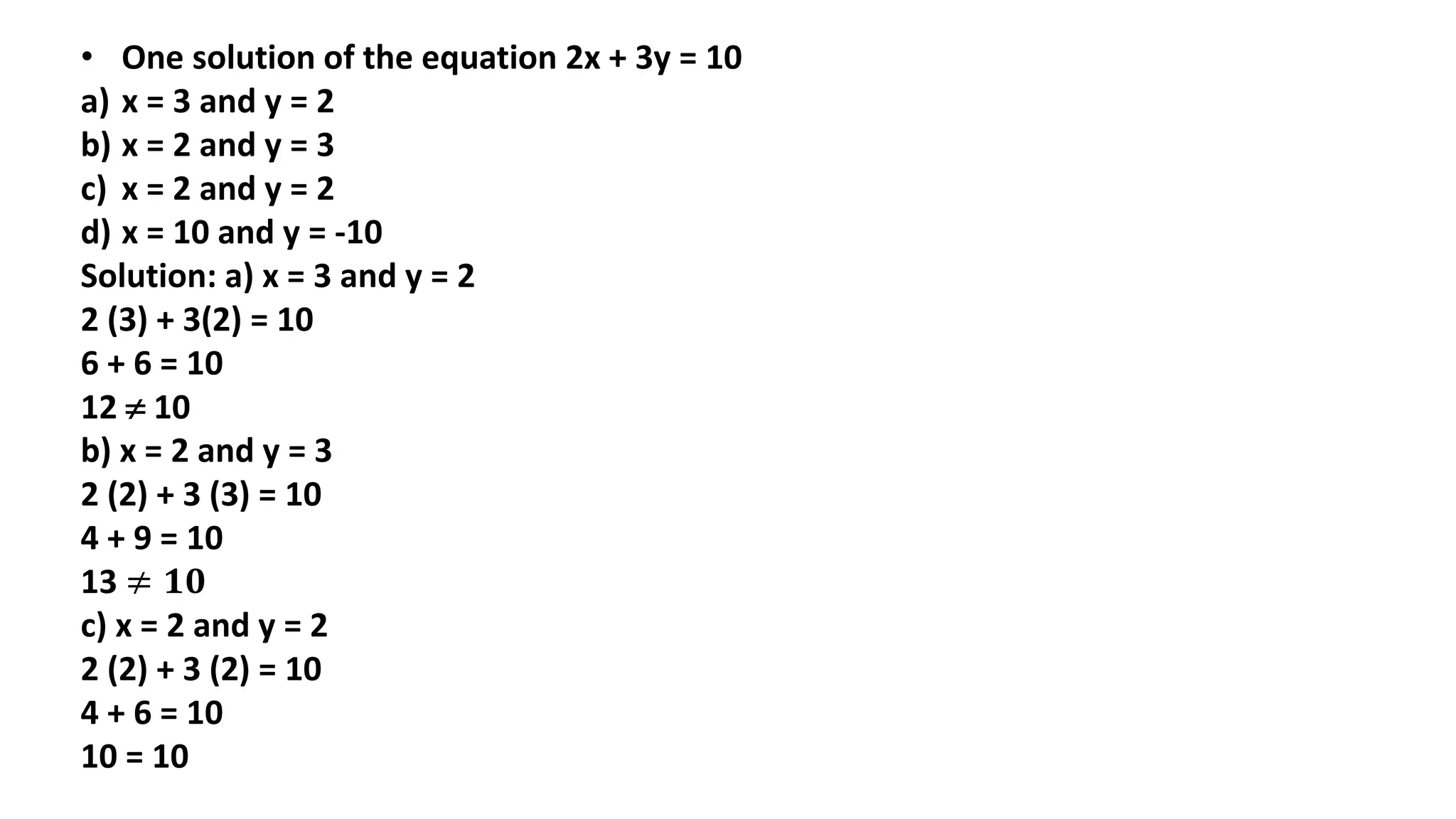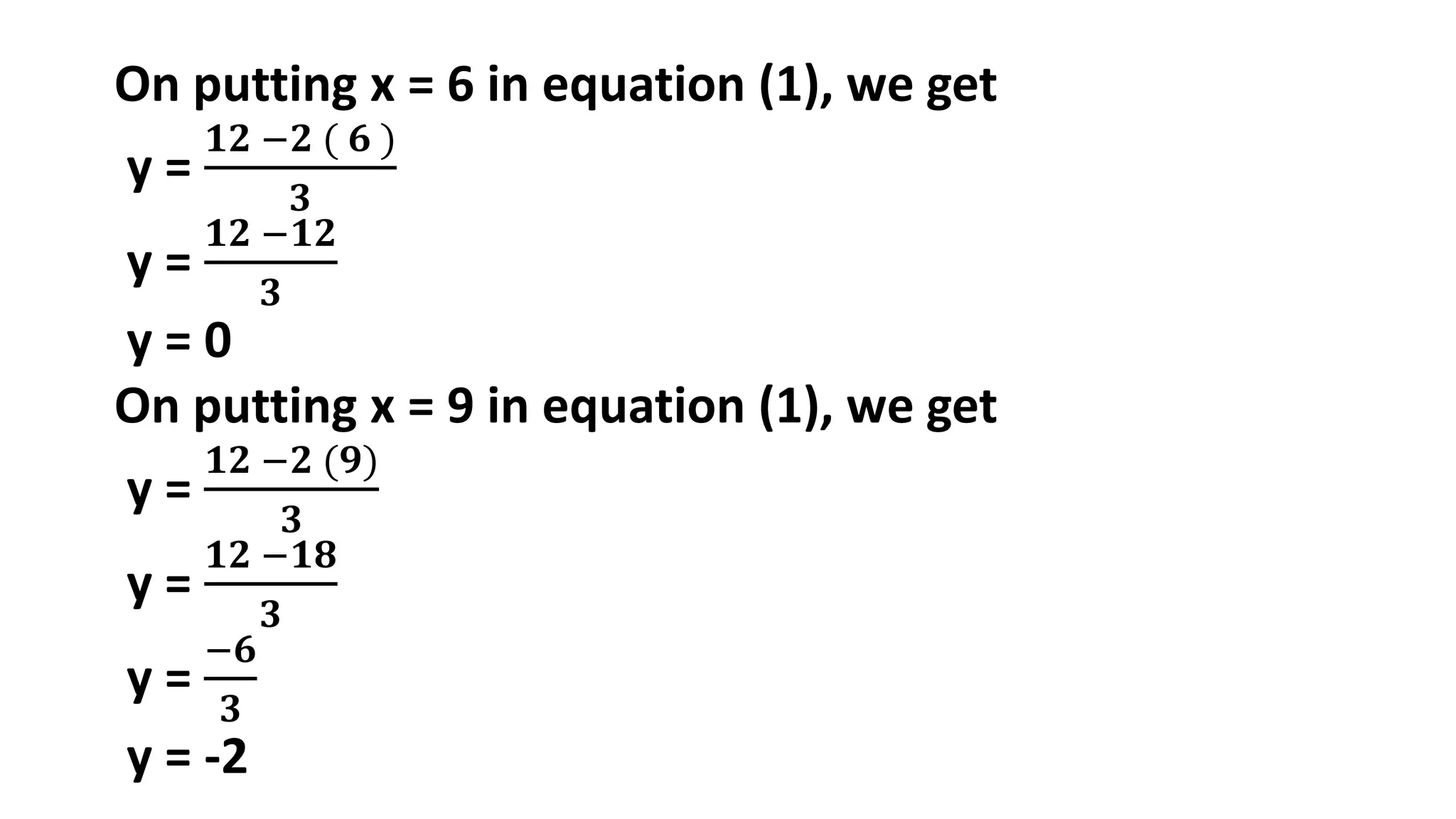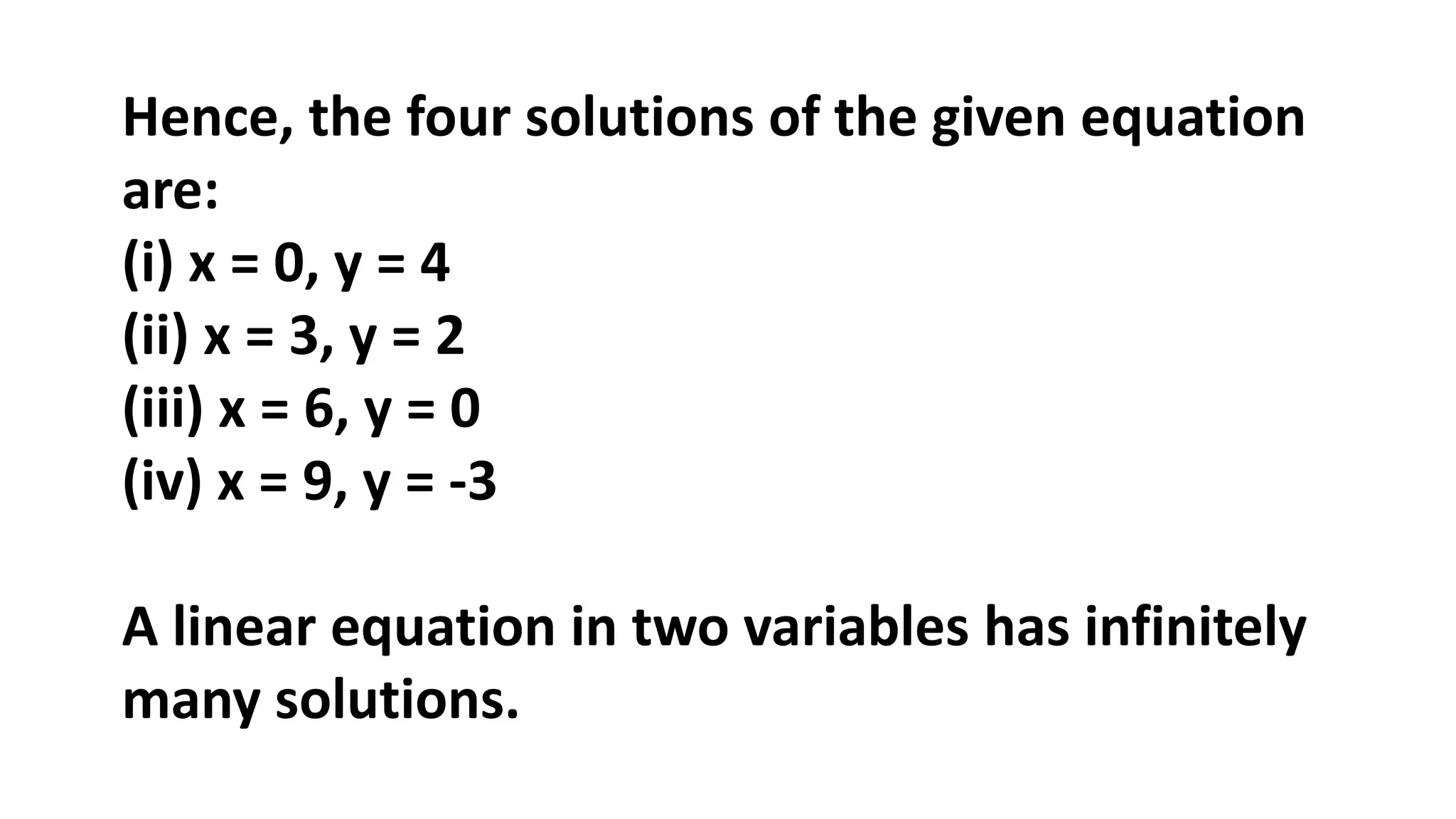The document discusses algebraic expressions, linear equations in one and two variables, providing definitions, examples, and methods to solve them. It explains how to find solutions to equations and illustrates with various examples, including the substitution method for simultaneous equations. Additionally, it highlights the graphical representation of equations and concludes with a quiz to reinforce knowledge.

2. • 5x
• 2x – 3
• 3x + y
• 2xy + 5
• xyz + x + y + z
• x2 + 1
• y + y2
Some examples of expressions

3. Algebraic Expressions

4. • 5x = 25
• 2x – 3 = 9
• 2y +
𝟓
𝟐
= 8
• 6z + 10 = -7
• 9x – 11 = 8
Some examples of equations

5. Equations use the equality (=) sign
If yes = equation 
If no = equation 

6. These are linear expressions:
• 2x
• 2x + 1
• 3y – 7
• 12 – 5z
These are not linear expressions
• 𝑥2
+ 1
• y+𝑦2
• 1+z+𝑧2
+𝑧3
(since highest
power of
variable > 1)
A linear expression is an
expression whose
highest power of the
variable is one only.

7. Linear Equations
The equation of a straight line is the linear equation. It could be in one
variable or two variables.
Linear Equation in One Variable
If there is only one variable in the equation then it is called a linear
equation in one variable.
The general form is
ax + b = c, where a, b and c are real numbers and a ≠ 0.

8. Example
x + 5 = 10
y – 3 = 19
These are called linear equations in one variable
because the highest degree of the variable is one and
there is only one variable.

9. • We assume that the two
sides of the equation are
balanced.
• We perform the same
mathematical operations on
both sides of the equation,
so that the balance is not
disturbed.
How to find the solution of an equation?

10. X + 3 = 7
X = 7
The value which when substituted for the
variable in the equation, makes its two
sides equal, is called a solution ( or root )
of the equation.

11. REMEMBER
• The same number can be added to both the sides of the
equation.
• The same number can be subtracted from both the sides of
the equation.
• We can multiply or divide both the sides of the equation by
the same non-zero number.

12. https://www.liveworksheets
.com/ng1353447tn

13. • Solve the linear equation: 4x + 3 = 15 – 2x
Solution: 4x + 3 = 15 – 2x
On subtracting 3 from both the sides, we get
4x + 3 – 3 = 15 – 2x – 3
Or,
4x = 12 – 2x
4x + 2x = 12 – 2x + 2x
6x = 12
𝟔𝒙
𝟔
=
𝟏𝟐
𝟔
X = 2
Hence, x = 2 is the solution of the given solution.

14. MATHEMATICS – I
CHAPTER – 1
LINEAR EUATIONS IN TWO
VARIABLES
CLASS X

15. • ax + b = c, where a, b and c are real numbers and
a ≠ 0.
Example ,
2x + 3 = 6
• ax + by + c = 0, where a, b and are real numbers,
such that a ≠ 0, b ≠ 0.
Example,
2x + 5y + 8 = 0
Linear equation in one variable
Linear equation in two variable

16. ax + by + c = 0, where a, b and c are
real numbers, such that a ≠ 0, b ≠ 0.
Example:
a) 4x + 3y = 4
b) -3x + 7 = 5y
c) X = 4y
d) Y = 2 – 3x

17. • Compare the equation ax + by + c = 0 with
equation 2x + 3y = 4.37 and find the values of a,
b and c?
a)a = 2, b = 3 and c = 4.37
b)a = 2, b = 3 and c = - 4.37
c)a = 2, b = -3 and c = - 4.37
d)a = -2, b = 3 and c = 4.37
Solution: b) a = 2, b = 3 and c = - 4.37
ax + by + c = 0
2x + 3y + (-4.37) = 0

18. Solution of a linear equations in two variable
The solution of a linear equation in two variables is an
ordered pair of numbers, which satisfies the equation.
The values x = m and y = n are said to be the solution of
the linear equation.
‘ax + by + c = 0’ if
am + bn + c = 0

19. • Show that x = 4 and y = -1 satisfy the equation x + 3y –
1 = 0
Solution:
On substituting x = 4 and y = -1 in equation x + 3y – 1 = 0,
we get
L. H. S = 4 + 3 X (-1) – 1
= 4 – 3 – 1
= 0
= R. H. S
Hence, x = 4 and y = -1 satisfy the equation x + 3y – 1 = 0.

20. Oranges + Apples = 10

21. Oranges Apples Fruits
1 9 10
2 8 10
3 7 10
4 6 10
5 5 10
6 4 10
7 3 10
8 2 10
9 1 10
Hit and Trial Method

22. Hint –
Apples are 2 more than oranges
6 Apples + 4 Oranges = 10
6 Apples – 4 Oranges = 2
x + y = 10
x – y = 2
(2 – Equations, 2 – Variables or 2 – Unknowns)
This pair of equation is called linear of equation in two
variables or
System of equation or simultaneous equations.
Algebraic or Graphical Method.

24. • If x = 1, y = 2 is a solution of the equation 3x + 2y = k,
then the value of k is
a) 7
b) 6
c) 5
d) 4
Solution: 3x + 2y = k
3 (1) + 2 (2) = k
3 + 4 = k
K = 7

25. • 𝑻𝒉𝒆 𝒄𝒐𝒎𝒎𝒐𝒏 𝒔𝒐𝒍𝒖𝒕𝒊𝒐𝒏 𝒐𝒇 𝟑𝒙 + 𝟐𝒚 = 𝟔 𝒂𝒏𝒅 𝟓𝒙 − 𝟐𝒚 = 𝟏𝟎 𝒊𝒔
a)(0,3)
b)(0,-5)
c)(2,0)
d)(1,0)
Solution:
3x + 2y = 6
5x – 2y = 10
+
-------------------------------
8 x + 0 = 16
x =
𝟏𝟔
𝟖
= 2
3x + 2y = 6
3 (2) + 2y = 6
6 + 2y = 6
2y = 6 – 6
2y = 0
Y = 0
(x, y) = (2,0)

26. • Solution of the linear equation (x-1) = (
𝟑
𝟒
)(x+1) – (
𝟏
𝟐
) will be
a) x = 5
b)x = 4
c) x = 3
d)x = 1
Solution: (x-1) = (
𝟑
𝟒
)(x+1) – (
𝟏
𝟐
)
x – 1 =
𝟑
𝟒
x +
𝟑
𝟒
-
𝟏
𝟐
x -
𝟑
𝟒
x =
𝟑
𝟒
-
𝟏
𝟐
+ 1
𝒙(𝟒−𝟑)
𝟒
=
(𝟔−𝟒)
𝟖
+ 1
𝒙
𝟒
=
𝟐
𝟖
+ 1
2x = 2 + 8
2x = 10
X = 5

27. • What is the value of x in the equation 𝟑 x – 2 = 2 𝟑 + 4
a) 2 ( 1 - 𝟑 )
b) 2 ( 1 + 𝟑 )
c) 1 + 𝟑
d) 1 - 𝟑
Solution – 𝟑 x – 2 = 2 𝟑 + 4
• 𝟑 x = 2 𝟑 + 4 + 2
• 𝟑 x = 2 𝟑 + 6
•
𝟑
𝟑
x =
𝟐 𝟑+ 𝟔
𝟑
• x = 2 +
𝟔
𝟑
• x = 2 + (
𝟔
𝟑
x
𝟑
𝟑
)
• x = 2 + (
𝟔
𝟑
x 𝟑 )
• x = 2 + 2 𝟑
• x = 2 ( 1 + 𝟑 )

28. • The value of x, which satisfies the equation 2.8 x – 0.8 x = 9 is
a)
𝟓
𝟐
b)
𝟗
𝟐
c)
𝟐
𝟓
d)
𝟐
𝟗
Solution:
8 x – 0.8 x = 9
2 x = 9
a) 2 (
𝟓
𝟐
) = 𝟗
5  9
b) 2 (
𝟗
𝟐
) = 9
9 = 9

29. • One solution of the equation 2x + 3y = 10
a) x = 3 and y = 2
b) x = 2 and y = 3
c) x = 2 and y = 2
d) x = 10 and y = -10
Solution: a) x = 3 and y = 2
2 (3) + 3(2) = 10
6 + 6 = 10
12  10
b) x = 2 and y = 3
2 (2) + 3 (3) = 10
4 + 9 = 10
13 ≠ 𝟏𝟎
c) x = 2 and y = 2
2 (2) + 3 (2) = 10
4 + 6 = 10
10 = 10

30. • The solution of the equation x + 3y = 12 will be
a) (2,3)
b) (1,2)
c) (3,3)
d) (4,2)
Solution:
a) (x, y) = (2,3)
x + 3y = 12 → 2 + 3(3) = 12
→ 2 + 9 = 12
→ 𝟏𝟏 ≠ 𝟏𝟐
b) (x, y) = (1,2)
x + 3y = 12 → 𝟏 + 3(2) = 12
→ 1 + 6 = 12
→ 𝟕 ≠ 𝟏𝟐
c) (x, y) = (3,3)
x + 3y = 12 → 𝟑 + 3(3) = 12
→ 3 + 9 = 12
→ 𝟏𝟐 = 𝟏𝟐

31. Summary
• An equation of the form ax + by + c = 0, where a, b, c
are real numbers, such that a ≠ 0, b ≠ 0. Is called
linear equation in two variable.
• Substitution method - The substitution method is the
algebraic method to solve simultaneous linear
equations. As the word says, in this method, the
value of one variable from one equation is
substituted in the other equation.

32. Glossary
Equation
Equation is a mathematical statement which shows that the value of two expression
are equal.
Linear equation in one variable
An equation which has the variable with the highest power one is called a linear
equation in one variable
Linear equation in two variable
An equation which can be put in the form ax + by + c = 0. where a, b and c are real
numbers and a and b both are not equal to zero, is called a linear equation in two
variables.
Solution of a linear equation in one variable
The value of a variable for which the given equation becomes true is known as
“Solution” or “Root’ of the equation.
Solution of a linear equation in two variable
A solution of the linear equation in two variables is an ordered pair of numbers,
which satisfies the equations.

33. LETS PLAY
QUIZIZZ

35. Example
Find the four solutions of the equation 2x + 3y – 12 = 0
Solution –
The given equation can be written as : y =
𝟏𝟐 −𝟐𝒙
𝟑
y =
𝟏𝟐 −𝟐𝒙
𝟑
. . . . . . . . . . ( 1 )
On putting x = 0 in equation (1), we get
y =
𝟏𝟐 −𝟐 ( 𝟎 )
𝟑
y =
𝟏𝟐
𝟑
= 4
On putting x = 3 in equation (1), we get
y =
𝟏𝟐 −𝟐 (𝟑)
𝟑
y =
𝟔
𝟑
y = 2

36. On putting x = 6 in equation (1), we get
y =
𝟏𝟐 −𝟐 ( 𝟔 )
𝟑
y =
𝟏𝟐 −𝟏𝟐
𝟑
y = 0
On putting x = 9 in equation (1), we get
y =
𝟏𝟐 −𝟐 (𝟗)
𝟑
y =
𝟏𝟐 −𝟏𝟖
𝟑
y =
−𝟔
𝟑
y = -2

37. Hence, the four solutions of the given equation
are:
(i) x = 0, y = 4
(ii) x = 3, y = 2
(iii) x = 6, y = 0
(iv) x = 9, y = -3
A linear equation in two variables has infinitely
many solutions.

38. Test Your Knowledge
Equation p = 2q + 3 has _____________
a)only one solution.
b)only two solutions.
c)infinitely many solutions.
d)no solution.