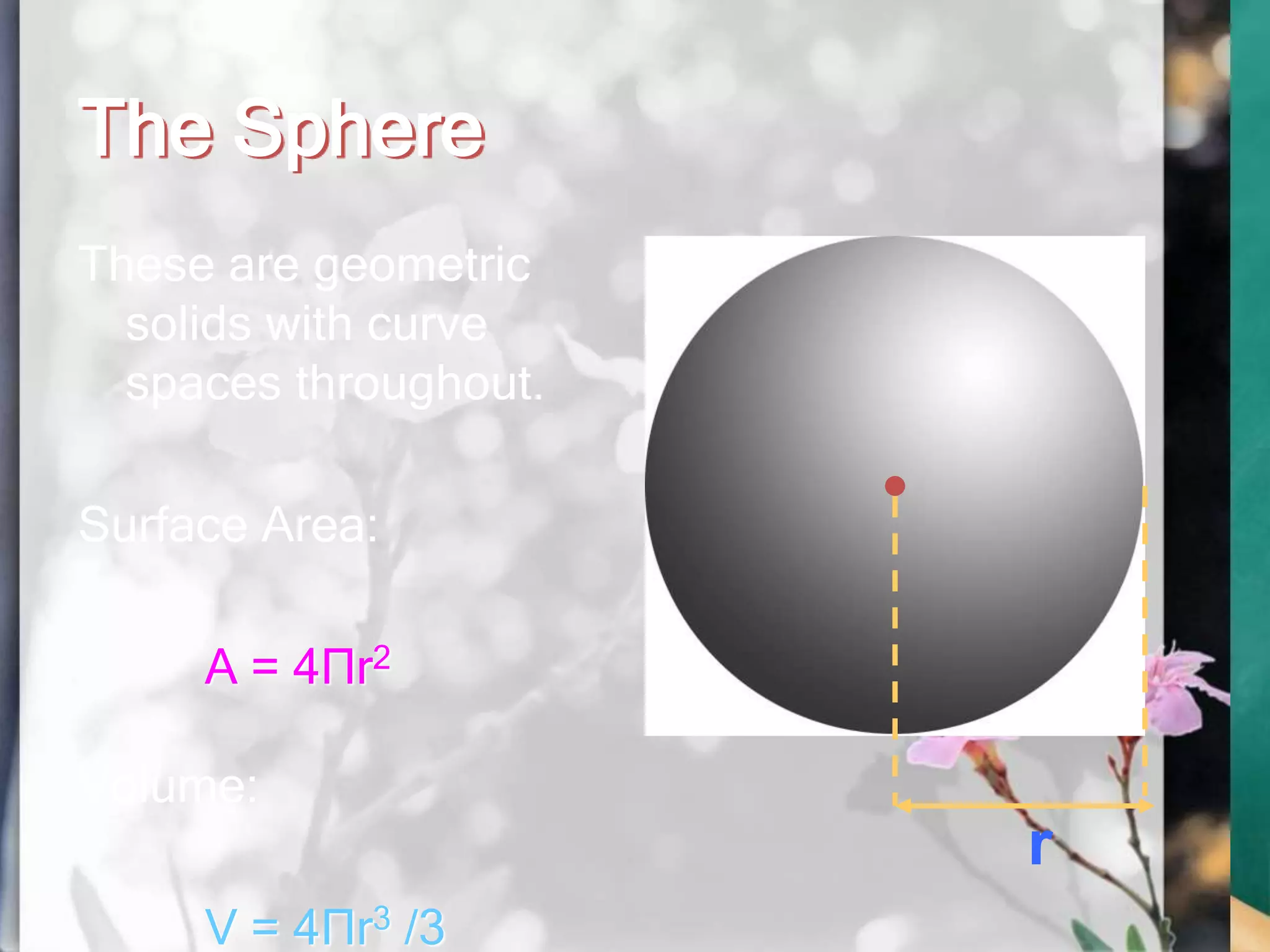
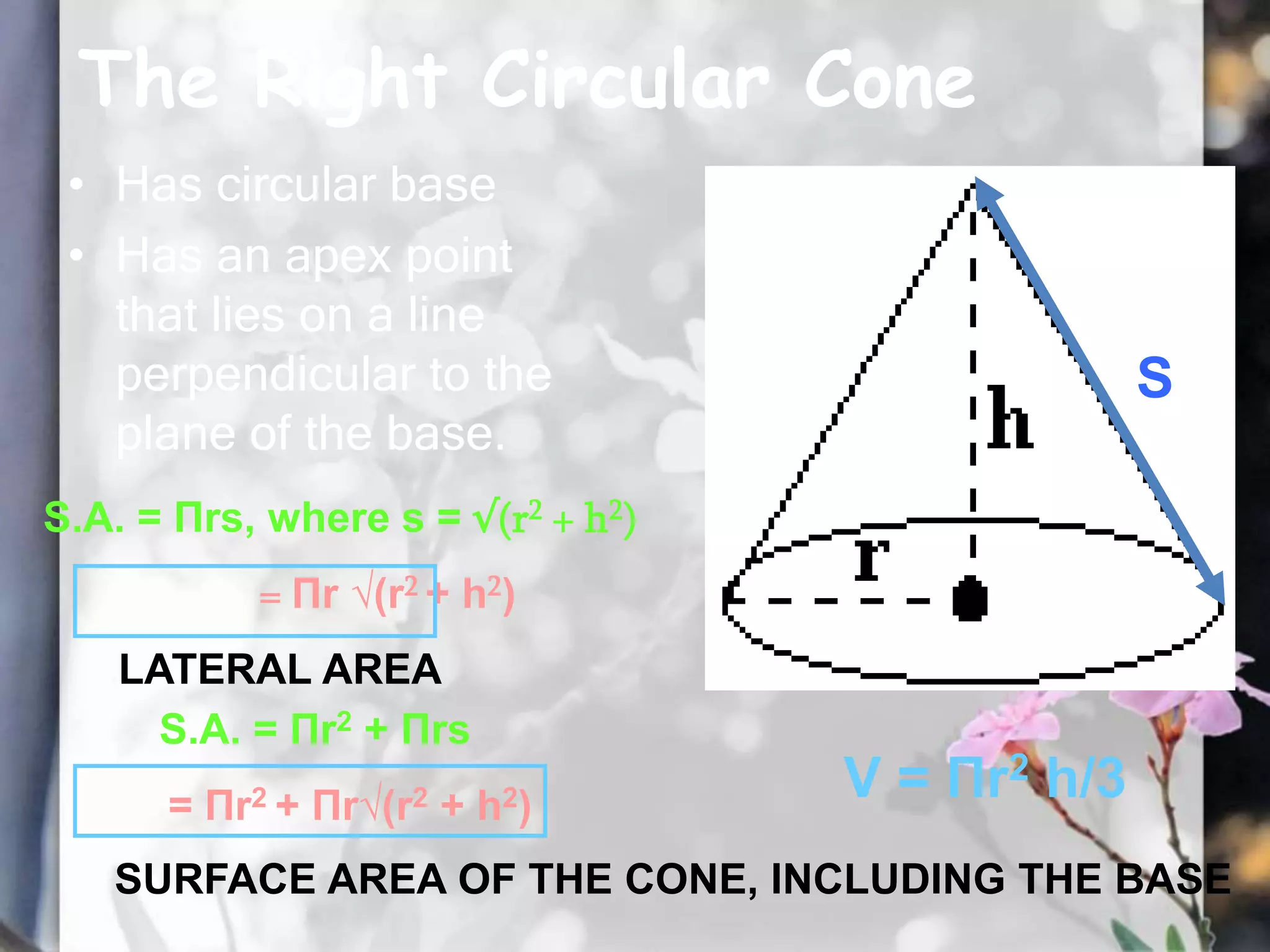
This document provides formulas and descriptions for calculating the volumes and surface areas of various 3D shapes. It includes formulas for rectangular prisms, rectangular pyramids, cubes, cuboids, right circular cones, frustums of right circular cones, slant circular cones, right circular cylinders, slant circular cylinders, and spheres. Diagrams are also provided to illustrate key features of each shape.

2. Group Members

3. arc length
sphere
parametric surfaces
calculus
partial derivatives double integration

4. Volume is the measure of the amount of space inside of a
solid figure, like a cube, ball, cylinder or pyramid. It's units
are always "cubic", that is, the number of little element
cubes that fit inside the figure.
The formula for the volume of a rectangular prism is:
Area = l x w x h
where:
l = length
w = width
h = height

5. Rectangular Pyramid
• Has rectangular base & 4
slanted faces.
• If the base is a square, &
if the apex lies directly
above a point at the
center of the base, then it
is a symmetrical
square pyramid.
S.A. = t2 + 2t √(s2 – t2/4)
V = Ah/3
s = slant height
t = edge of the base

6. The Cube
• It is a regular
hexahedron
• Has 12 edges & 6
faces
S.A. = 6s2
V = s3

7. CUBOID
• A hexahedron that
has 6 rectangular
faces.
• Has 12 edges but not
necessarily of the
same length.
Surface Area = 2lb + 2bh + 2hl
Volume = lbh
l
b
h

8. Cones and Cylinders
• A cone has a circular or
elliptical base and an
apex point.
• A cylinder has a circular
or elliptical base, & a
circular or elliptical top
that is congruent to the
base & that lies in a
plane parallel to the
base.
Right circular cone
Frustum of Right circular
cone
Slant circular cone
Right circular cylinder
Slant circular cylinder

9. The Right Circular Cone
• Has circular base
• Has an apex point
that lies on a line
perpendicular to the
plane of the base.
S.A. = Πrs, where s = √(r2 + h2)
= Πr √(r2 + h2)
S.A. = Πr2 + Πrs
= Πr2 + Πr√(r2 + h2)
V = Πr2 h/3
S
LATERAL AREA
SURFACE AREA OF THE CONE, INCLUDING THE BASE

10. Frustum of Right Circular Cone
• It is when a right
circular cone was
truncated by a plane
parallel to the base.
S.A. = Π(r2 + r2) √[h2 + (r2 – r1)2] + Π(r1
2 + r2
2),
where s = √[h2 + (r2 – r1)2], then
= Πs(r2 + r2) + Π (r1
2 + r2
2)
S.A. = Π(r1 + r2) √[h2 + (r2 – r1)2]
where s = √[h2 + (r2 – r1)2], then
= Πs(r1 + r2)
V = Πh( r1
2 +r1r2 + r2
2)/3
S.A. INCLUDING THE
TOP & THE BASE
S.A. EXCLUDING THE
TOP & THE BASE

11. The Slant Circular Cone
• Has circular base
• Has an apex point
that does not pass
through the center of
the base
V = Πr2 h/3
r
h

12. The Right Circular Cylinder
• Has circular base &
circular top.
• The base & the top lie
in a parallel planes
S.A. = 2Πrh + 2Πr2 or
= 2Πr (h + r)
S.A. = 2Πrh
V = Πr2 h
S.A. INCLUDING THE BASE
S.A. EXCLUDING THE BASE

13. The Slant Circular Cylinder
• It has circular base
and circular top
• The base & the top lie
in parallel planes
V = Πr2 h
r
h

14. The Sphere
These are geometric
solids with curve
spaces throughout.
Surface Area:
A = 4Πr2
Volume:
V = 4Πr3 /3
r