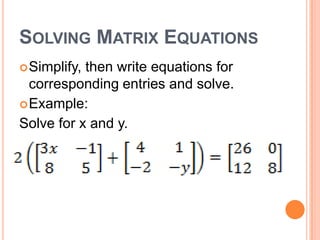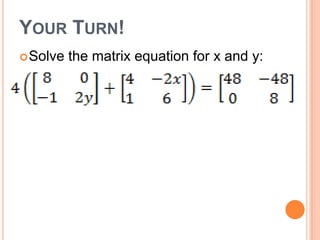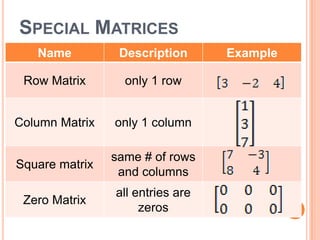
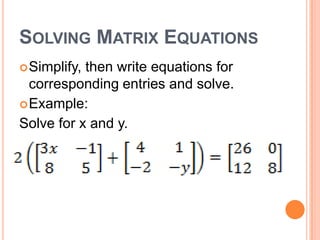
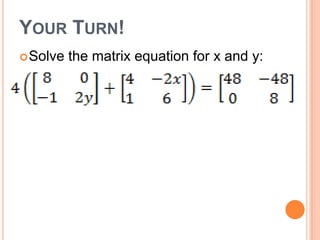
This document defines and provides examples of matrix operations including addition, subtraction, multiplication by a scalar, and solving matrix equations. A matrix is an arrangement of numbers in rows and columns. Special types of matrices include row matrices, column matrices, square matrices, and zero matrices. Two matrices are equal if their dimensions are the same and corresponding entries are equal. Matrix addition and subtraction involve adding or subtracting the corresponding entries of matrices of the same dimensions. Multiplication by a scalar involves multiplying each entry of the matrix by the scalar value. Solving matrix equations involves writing equations for corresponding entries and solving them.

1. 4.1 MATRIX OPERATIONS

2. WHAT IS A MATRIX?
A group of numbers arranged in rows
and columns.
 Its numbers are called entries or
elements.
 The dimensions are:
# of rows x # of columns
 Example:
 This matrix has dimension 2 x 3

3. SPECIAL MATRICES
Name Description Example
Row Matrix only 1 row
Column Matrix only 1 column
same # of rows
Square matrix
and columns
all entries are
Zero Matrix
zeros

4. COMPARING MATRICES
 Two matrices are equal if their dimensions
are the same and corresponding entries are
equal.
 Are these equal?

5. ADDING AND SUBTRACTING MATRICES
 Dimensions must match!
 Add or subtract corresponding entries.
 Examples:
Not Possible!

6. YOUR TURN!
 Perform the indicated operation, if possible.
a.
b.
c.

7. MULTIPLYING BY A SCALAR
 Scalar – a regular number
 Scalar multiplication – multiplying a
matrix by a scalar
 Just multiply each entry by the scalar!
Example:

8. EXAMPLE:
 Perform the indicated operation(s), if
possible.

9. YOUR TURN!
 Perform the indicated operation(s).

10. SOLVING MATRIX EQUATIONS
 Simplify,then write equations for
corresponding entries and solve.
 Example:
Solve for x and y.

11. YOUR TURN!
 Solve the matrix equation for x and y: