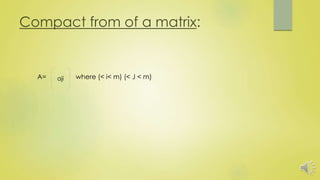This document provides an overview of matrices including: - Definitions of matrices, order of matrices, and compact matrix form - Matrix multiplication and checking compatibility of matrices - Determinants, adjoints, and inverses of matrices - Methods for solving systems of equations using matrices including Gauss-Jordan elimination and Cramer's rule The document also provides brief biographies of James Joseph Sylvester and Arthur Cayley, two mathematicians who made important contributions to the field of matrices.

2. Contents
 History of matrices
 Introduction of matrices
 Definition of matrix
 Matrix Multiplication
 Row & column
 Order of matrix
 Compact form of matrix
 Determinants of ad joint inverse of a matrix
 Ad joint Matrix
 Inverse Matrix
 Inverse Matrix Method
 Gauss-Jordan's Metod
 Steps to convert the augmented matrix into fins=al matrix & get solutions

3. James Joseph Sylvester:
He was British mathematician. He was born in London ,England.
His father Abraham joseph was a merchant. James adopted the summaries
Sylvester when his older brother did so uponemringtion united states at age of
14. Sylvester was a student of Augustus de Morgan at the university of
London.
Arthur Clayey:
He was British mathematician who helped founding the British
school of pure mathematics. Although clayey was born in England, his first
seven years were spent in St. Petersburg Russian where his parents lived in the
family permanent return to England in 1828. He was educated at a small
private school in blackheart followed by the three - years course at king
college, London.

4. Matrices
Definition of MATRIX:
A matrix in general sense, represents a collection of
information stored or arranged in an orderly fashion.
Application of Matrices:
There are numerous application of matrices, both in
mathematics and other sciences. Some of them, game theory and
economics, text mining and automated thesaurus compilation
computer graph theory, network theory makes use of matrices in
various way.

5. Matrix Multiplication
Scalar Multiplication
Consider the following
If s is a scalar and A is a matrix
1 5
s = 2, and A = 4 3
2 1
1 5 2(1) 2(5) 210
sA = 2 * 4 3 = 2(4) 2(3) = 8 6
2 1 2(2) 2(1) 4 2
Rule: If s is a scalar and A is a matrix, then the scalar multiple sA is the matrix whose columns are s
times the corresponding entries in A. In other words, you take the scalar and multiply it with every number in
the matrix.
Theorem: If r and s are scalars, then (r + s)A = rA + sA and r(sA) = (rs)A.

6. Matrix Multiplication
Before you multiply a matrix by another matrix, you need to check the compatibility of the two matrices. The number
of columns (n) in A must equal the number of rows (m) in B in order to carry out the matrix
multiplication.
Example 1 :
A = 2 5 B = 3 1 7
1 3 8 2 4
m * n m * n
2 * 2 2 * 3
You can see that the number of columns of A matches the number of rows of B. (Later on, you will see that the size
of matrix AB will be m of A × n of B).
Example 2 :
A = 2 5 B = 3 1 7
1 3 8 2 4
4 1 2
2 * 2 3 * 3
Obviously, n of A ≠ m of B and thus they are not compatible for multiplication.

7. Definition:
A collection of number (real or complex) are arranged in the
from of a rectangular or square array (arrangement) in horizontal and
vertical lines is called a Matrix.
 Row:
 The horizontal lines of number in a matrix are called “row”
 Columns:
 The vertical lines of number in a matrix are called
“columns”
7 3 2 -5
8 2 -1 4
2
1-I
1+2I

8. Order of matrix:
The order of a matrix is defined in term of its number of rows and
columns.
Order of matrix = No of rows * No . of Columns
1
2
3
0
9
2

9. Compact from of a matrix:
A= where (< i< m) (< J < m)aji

10. Determinants(Ad joint& Inverse of a
matrix)
 Singular:
 A singular matrix is said to be a “singular matrix” if det A=0
 EX: A =
 A =10 * 4-5 * 8 = 40-40=0
 Non –singular:
 A square matrix A is said to be a “non singular” if det
A 0
 EX: A =
 A =1 * 1-2 * 3 =1- 6 = -5 0
10 5
8 4
1 2
3 1

11. Adjoins matrix
Definition :
If the element of a square matrix are replaced by elements
then the transpose of the result matrix is called Ad jont matrix.
A =
A11 A12 A13
A21A22 A23
A31 A23 A33

12. Inverse of matrix
Definition:
Let A be a non –singular matrix. If there exists a square matrix
B = AB =1
A 1 =AdjA/detA

13. Invers matrix method
Let
A =
X = B=
X =A 1 B
A 1 =1 /det * Adj A
a1 b1 c1
a2 b2 c2
a3 b3 c3
X
Y
z
d1
d2
d3

14. Gauss-Jordan`s method
 Write down the Augmented
Matrix:
 Apply “Elementary Row
transformations” and reduce the
Augmented matrix into the final
matrix
 Then is the
required solution.
a1 b1 c1 d1
a2 b2 c2 d2
a3 b3 c3 d3
1 0 0 a
0 1 0 b
0 0 1 c
x=a y=b z=c

15. Steps of the Augmented matrix into
Final Matrix & get solution:
 Step1:
In the Final matrix the 1st column is So, first concentrate
on 1st row and 1st column element in the Augmented matrix.
1 using k R1 (or)Ri ↔ Rj operation .
 Step2:
→ 1st column of Final matrix.
→ To get this 0 use R2 – kR1
→ To get this 0 use R3 ─ kR1
 Step3: Now concentrate on 2nd column of Final matrix . Make the
element in 2nd row &2nd column as 1 st using kR2 (or) R2↔R3
operation.
1
0
0
1
0
0

16.  Step4:
→ 2nd column in final Matrix
→ To get this 0 use R1- kR2
→ To get this 0 use R3- kR2
 Step5: Now concentrate on 3rd of Matrix . make the element in 3rd Row &3rd
column as 1 using kR3 operation.
 Step6:
→ 3rd column of Final Matrix
→ To get this 0 use R1 – KR3
 Step7:
Get the solution from the element obtained in the last column of
final Matrix x=a y=b z=c
0
1
0
0
0
1

17. Cramer's rule
 Solving the given equation: a1x+b1y+c1z=d1
a2x+b2y+c2z=d2
a3x+b3y+c3z=d3
 ▲ = a1 b1 c1 ▲1 =d1 b1 c1 ▲2 = a1 d1 c1
a2 b2 c2 ≠0 d2 b2 c2 a2 d2 c3
a3 b3 c3 d3 b3 c3 a3 d3 c3
 ▲3 =a1 b1 d1
a2 b2 d2
a3 b3 d3
x=▲1/▲: y=▲2/▲: z=▲3/▲

18. Royal CIVIL
Presented by
B.Lokeshwar.