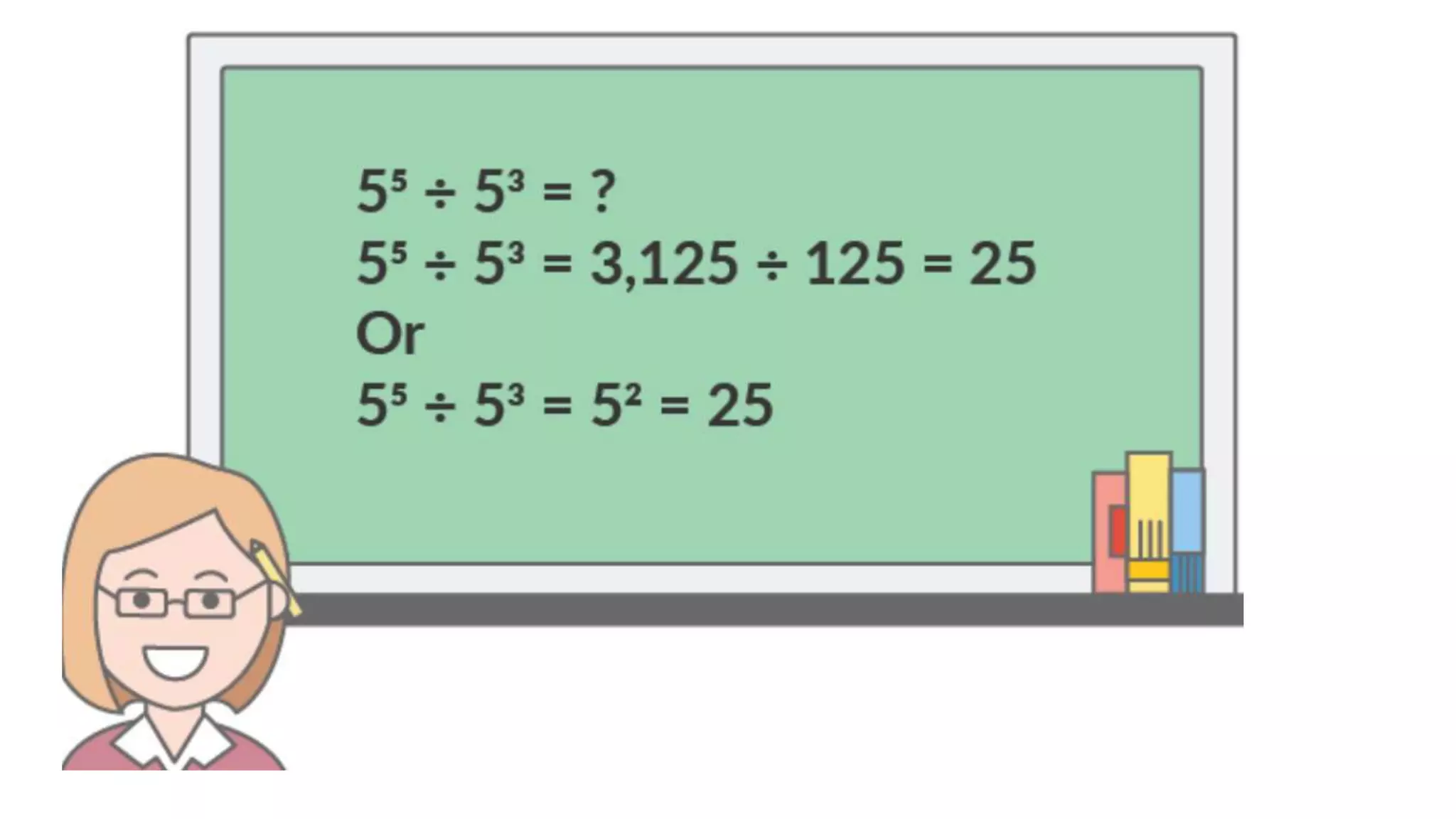
This document discusses exponents and powers, which provide a simple way to represent large numbers. It outlines 7 rules for working with exponents: 1) Product of powers, 2) Quotient of powers, 3) Power of a power, 4) Power of a product, 5) Power of a quotient, 6) Zero power, and 7) Negative exponent. These rules explain how to simplify expressions involving exponents through distributing, adding, subtracting, multiplying, or dividing the exponents.

1. ACE Learning Hub
Erode 638 011
Mob:93600 48588
chandkec@gmail.com

3. Dealing with big numbers is not so easy. But, we do use very big numbers
in reality.
Some examples where we use large numbers in real life situations:
• The distance between the Earth and the Sun is 149600000000 m.
• Mass of the Earth is 5970000000000000000000000 kg.
• The speed of light is 299792000 m/sec.
• The distance between Moon and the Earth is 384467000 m.
Exponents and powers is asimple and nice way to represent such
numbers.
Introduction

4. Exponents and Powers :
We can write large numbers in simplified form as given below.
For example, 16 = 8 x 2 = 4 x2 ×2 =2x 2x2x2x2
Instead of writing the factor 2 repeatedly 4 times, we can simply write
it as 2^4 .
It can be read as 2 raised to the power of 4 or 2 to the power of 4 or
simply 2 power 4.

5. 1. Product of powers rule
When multiplying two bases of the same value,
keep the bases the same and then add the exponents together to get
the solution.
42 × 45 = ?
Since the base values are both four, keep them the same
Then add the exponents (2 + 5) together.
42× 45 = 47
Then multiply four by itself seven times to get the answer.
47 = 4 × 4 × 4 × 4 × 4 × 4 × 4 = 16,384

6. (4𝒙2)(2𝒙3) = ?
Multiply the coefficients together (four and two), as they are not
the same base.
Then keep the ‘𝒙’ the same and add the exponents.(4𝒙2)(2𝒙3) = 8𝒙5

7. 2. Quotient of powers rule
• Multiplication and division are opposites of each other
• The quotient rule acts as the opposite of the product rule.
• When dividing two bases of the same value, keep the base the same,
and then subtract the exponent values.
55 ÷ 53 = ?
Both bases in this equation are five, which means they stay the same.
Then, take the exponents and subtract the divisor from the dividend.
55 ÷ 53 = 52
Finally, simplify the equation if needed:52 = 5 × 5 = 25

9. 3. Power of a power rule
This rule shows how to solve equations where a power is
being raised by another power.
(𝒙3)3 = ?
In equations like this multiply the exponents together and keep
the base the same.(𝒙3)3 = 𝒙9

11. 4. Power of a product rule
• When any base is being multiplied by an
exponent, distribute the exponent to each part of the base.
(𝒙𝑦)3 = ?
In this equation, the power of three needs to be distributed to
both the 𝒙 and the 𝑦 variables.
(𝒙𝑦)3 = 𝒙3𝑦3
This rule applies if there are exponents attached to the base
as well.
(𝒙2𝑦2)3 = 𝒙6𝑦6

12. Both of the
variables
are squared in this
equation and are
being raised to the
power of three.
That means three is
multiplied to the
exponents in both
variables turning
them into variables
that are raised to
the power of six.

13. 5. Power of a quotient rule
A quotient simply means that you’re dividing two quantities.
In this rule, you’re raising a quotient by a power.
The exponent needs to be distributed to all values within the
brackets it’s attached to.
(𝒙/𝑦)4 = ?
Here, raise both variables within the brackets by the power of
four.

15. 6. Zero power rule
Any base raised to the power of zero is equal to one.
No matter how long the equation, anything raised to the power
of zero becomes one.(82𝒙4𝑦6)0 = ?

16. 7. Negative exponent rule
When there is a number being raised by a negative exponent, flip
it into a reciprocal to turn the exponent into a positive.
Don’t use the negative exponent to turn the base into a negative.
Example:𝒙-2 = ?
To make a number into a reciprocal:
1.Turn the number into a fraction (put it over one)
2.Flip the numerator into the denominator and vice versa
3.When a negative number switches places in a fraction it becomes a
positive number

17. 4𝒙-3𝑦2/20𝒙𝑧-3 = 𝑦2𝑧3/5𝒙4