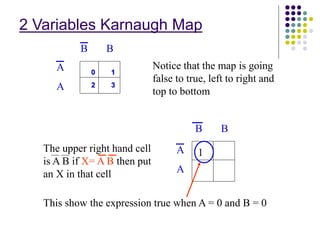
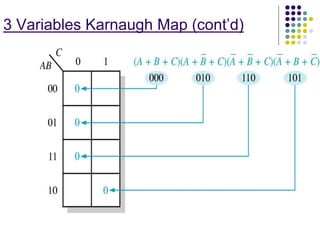
This document provides an overview of Boolean algebra and logic simplification. It defines Boolean operations and variables, lists laws and rules of Boolean algebra including De Morgan's theorems. It also explains standard forms of Boolean expressions, truth tables, and how to use Karnaugh maps to minimize logic expressions in sum of products or product of sums form. Karnaugh maps allow grouping variables to simplify expressions for 2, 3, 4 or more variables.

1. DKT 122 / 3
DIGITAL SYSTEMS 1
CHAPTER 4 :
BOOLEAN ALGEBRA AND LOGIC
SIMPLIFICATION
m.rizal@unimap.edu.my
sitizarina@unimap.edu.my

2. 4.0 BOOLEAN ALGEBRA
 Boolean Operations & expression
 Laws & rules of Boolean algebra
 DeMorgan’s Theorems
 Boolean analysis of logic circuits
 Simplification using Boolean Algebra
 Standard forms of Boolean Expressions
 Boolean Expressions & truth tables
 The Karnaugh Map

3.  Karnaugh Map SOP minimization
 Karnaugh Map POS minimization
 5 Variable K-Map
 Programmable Logic

4. •Boolean Operations & expression
 Expression :
 Variable – a symbol used to represent logical
quantities (1 or 0)
ex : A, B,..used as variable
 Complement – inverse of variable and is indicated by
bar over variable
ex : Ā

5.  Operation :
 Boolean Addition – equivalent to the OR operation
 X = A + B
- Boolean Multiplication – equivalent to the AND operation
 X = A∙B
A
B
X
A
B
X

6. Laws & rules of Boolean
algebra

7. Commutative law of addition
Commutative law of addition,
A+B = B+A
the order of ORing does not matter.

8. Commutative law of Multiplication
Commutative law of Multiplication
AB = BA
the order of ANDing does not matter.

9. Associative law of addition
Associative law of addition
A + (B + C) = (A + B) + C
The grouping of ORed variables does not
matter

10. Associative law of multiplication
Associative law of multiplication
A(BC) = (AB)C
The grouping of ANDed variables does not
matter

11. Distributive Law
A(B + C) = AB + AC
(A+B)(C+D) = AC + AD + BC + BD

12. Boolean Rules
1) A + 0 = A
 In math if you add 0 you have changed nothing
 In Boolean Algebra ORing with 0 changes nothing

13. Boolean Rules
2) A + 1 = 1
 ORing with 1 must give a 1 since if any input
is 1 an OR gate will give a 1

14. Boolean Rules
3) A • 0 = 0
 In math if 0 is multiplied with anything you
get 0. If you AND anything with 0 you get 0

15. Boolean Rules
4) A • 1 = A
 ANDing anything with 1 will yield the anything

16. Boolean Rules
5) A + A = A
 ORing with itself will give the same result

17. Boolean Rules
6) A + A = 1
 Either A or A must be 1 so A + A =1

18. Boolean Rules
7) A • A = A
 ANDing with itself will give the same result

19. Boolean Rules
8) A • A = 0
 In digital Logic 1 =0 and 0 =1, so AA=0 since one of
the inputs must be 0.

20. Boolean Rules
9) A = A
 If you not something twice you are back to the
beginning

21. Boolean Rules
10) A + AB = A
Proof:
A + AB = A(1 +B) DISTRIBUTIVE LAW
= A∙1 RULE 2: (1+B)=1
= A RULE 4: A∙1 = A

22. Boolean Rules
11) A + AB = A + B
 If A is 1 the output is 1 , If A is 0 the output is B
Proof:
A + AB = (A + AB) + AB RULE 10
= (AA +AB) + AB RULE 7
= AA + AB + AA +AB RULE 8
= (A + A)(A + B) FACTORING
= 1∙(A + B) RULE 6
= A + B RULE 4

23. Boolean Rules
12) (A + B)(A + C) = A + BC
PROOF
(A + B)(A +C) = AA + AC +AB +BC DISTRIBUTIVE LAW
= A + AC + AB + BC RULE 7
= A(1 + C) +AB + BC FACTORING
= A.1 + AB + BC RULE 2
= A(1 + B) + BC FACTORING
= A.1 + BC RULE 2
= A + BC RULE 4

24. De Morgan’s Theorem,

25. Theorems of Boolean Algebra
1) A + 0 = A
2) A + 1 = 1
3) A • 0 = 0
4) A • 1 = A
5) A + A = A
6) A + A = 1
7) A • A = A
8) A • A = 0

26. Theorems of Boolean Algebra
9) A = A
10) A + AB = A
11) A + AB = A + B
12) (A + B)(A + C) = A + BC
13) Commutative : A + B = B + A
AB = BA
14) Associative : A+(B+C) =(A+B) + C
A(BC) = (AB)C
15) Distributive : A(B+C) = AB +AC
(A+B)(C+D)=AC + AD + BC + BD

27. De Morgan’s Theorems
16) (X+Y) = X . Y
17) (X.Y) = X + Y
• Two most important theorems of Boolean
Algebra were contributed by De Morgan.
• Extremely useful in simplifying expression in
which product or sum of variables is inverted.
• The TWO theorems are :

28. Implications of De Morgan’s Theorem
(a) Equivalent circuit implied by theorem (16)
(b) Alternative symbol for the NOR function
(c) Truth table that illustrates DeMorgan’s Theorem
(a)
(b)
Input Output
X Y X+Y XY
0 0 1 1
0 1 0 0
1 0 0 0
1 1 0 0
(c)

29. Implications of De Morgan’s Theorem
(a) Equivalent circuit implied by theorem (17)
(b) Alternative symbol for the NAND function
(c) Truth table that illustrates DeMorgan’s Theorem
(a)
(b)
Input Output
X Y XY X+Y
0 0 1 1
0 1 1 1
1 0 1 1
1 1 0 0
(c)

30. De Morgan’s Theorem Conversion
Step 1: Change all ORs to ANDs and all ANDs to Ors
Step 2: Complement each individual variable
(short overbar)
Step 3: Complement the entire function (long overbars)
Step 4: Eliminate all groups of double overbars
Example : A . B A .B. C
= A + B = A + B + C
= A + B = A + B + C
= A + B = A + B + C
= A + B

31. ABC + ABC (A + B +C)D
= (A+B+C).(A+B+C) = (A.B.C)+D
= (A+B+C).(A+B+C) = (A.B.C)+D
= (A+B+C).(A+B+C) = (A.B.C)+D
= (A+B+C).(A+B+C) = (A.B.C)+D
De Morgan’s Theorem Conversion

32. Examples: Analyze the circuit below
Y
1. Y=???
2. Simplify the Boolean expression found in 1

33.  Follow the steps list below (constructing truth
table)
 List all the input variable combinations of 1 and 0
in binary sequentially
 Place the output logic for each combination of
input
 Base on the result found write out the boolean
expression.

34. Standard Forms of Boolean Expressions
Sum of Products (SOP) Products of Sum (POS)
Notes:
 SOP and POS expression cannot have more than
one variable combined in a term with an inversion bar
 There’s no parentheses in the expression

35. Standard Forms of Boolean Expressions
Converting SOP to Truth Table
 Examine each of the products to determine where
the product is equal to a 1.
 Set the remaining row outputs to 0.

36. Standard Forms of Boolean Expressions
Converting POS to Truth Table
 Opposite process from the SOP expressions.
 Each sum term results in a 0.
 Set the remaining row outputs to 1.

37. Standard Forms of Boolean Expressions
BC
A
C
AB
C
B
A
C
B
A
f 


)
,
,
(
6
3
2
)
,
,
( m
m
m
C
B
A
f 


)
6
,
3
,
2
(
)
,
,
( m
C
B
A
f 

The standard SOP Expression
 All variables appear in each product term.
 Each of the product term in the expression is called
as minterm.
 Example:
 In compact form, f(A,B,C) may be written as

38. Standard Forms of Boolean Expressions
)
(
)
(
)
(
)
,
,
( C
B
A
C
B
A
C
B
A
C
B
A
f 








The standard POS Expression
 All variables appear in each product term.
 Each of the product term in the expression is called as
maxterm.
 Example:
5
4
1
)
,
,
( M
M
M
C
B
A
f 
 In compact form, f(A,B,C) may be written as
)
5
,
4
,
1
(
)
,
,
( M
C
B
A
f 


39. Standard Forms of Boolean Expressions
)
(
)
(
)
(
)
(
)
,
,
( C
B
A
C
B
A
C
B
A
C
B
A
C
B
A
f 











C
B
A
C
B
A
C
AB
ABC
C
B
A
f 



)
,
,
(
Example:
Convert the following SOP expression to an equivalent
POS expression:
Example:
Develop a truth table for the expression:

40. THE K-MAP

41. Karnaugh Map (K-Map)
 Karnaugh Mapping is used to minimize the number
of logic gates that are required in a digital circuit.
 This will replace Boolean reduction when the
circuit is large.
 Write the Boolean equation in a SOP form first and
then place each term on a map.

42. • The map is made up of a table of every possible
SOP using the number of variables that are being
used.
• If 2 variables are used then a 2X2 map is used
• If 3 variables are used then a 4X2 map is used
• If 4 variables are used then a 4X4 map is used
• If 5 Variables are used then a 8X4 map is used
Karnaugh Map (K-Map)

43. K-Map SOP Minimization

44. A
A
B B
Notice that the map is going
false to true, left to right and
top to bottom
The upper right hand cell
is A B if X= A B then put
an X in that cell
A
A
B B
1
This show the expression true when A = 0 and B = 0
0 1
2 3
2 Variables Karnaugh Map

45. If X=AB + AB then
put an X in both of
these cells
A
A
B B
1
1
From Boolean reduction we know that A B + A B = B
From the Karnaugh map we
can circle adjacent cell and
find that X = B
A
A
B B
1
1
2 Variables Karnaugh Map

46. 3 Variables Karnaugh Map
Gray Code
00 A B
01 A B
11 A B
10 A B
0 1
C C
0 1
2 3
6 7
4 5

47. X = A B C + A B C + A B C + A B C
Gray Code
00 A B
01 A B
11 A B
10 A B
0 1
C C
One
simplification
could be
X = A B + A B
1 1
1 1
3 Variables Karnaugh Map (cont’d)

48. X = A B C + A B C + A B C + A B C
Gray Code
00 A B
01 A B
11 A B
10 A B
0 1
C C
Another
simplification
could be
X = B C + B C
A Karnaugh
Map does wrap
around
1 1
1 1
3 Variables Karnaugh Map (cont’d)

49. X = A B C + A B C + A B C + A B C
Gray Code
00 A B
01 A B
11 A B
10 A B
0 1
C C
The Best
simplification
would be
X = B
1 1
1 1
3 Variables Karnaugh Map (cont’d)

50. On a 3 Variables Karnaugh Map
• One cell requires 3 Variables
• Two adjacent cells require 2 variables
• Four adjacent cells require 1 variable
• Eight adjacent cells is a 1

51. 4 Variables Karnaugh Map
Gray Code
00 A B
01 A B
11 A B
10 A B
0 0 0 1 1 1 1 0
C D C D C D C D
0 1 3 2
4 5 7 6
12 13 15 14
8 9 11 10

52. Gray Code
00 A B
01 A B
11 A B
10 A B
0 0 0 1 1 1 1 0
C D C D C D C D
1
1
1
1
1
1
X = ABD + ABC + CD
Now try it
with Boolean
reductions
Simplify :
X = A B C D + A B C D + A B C D + A B C D +
A B C D + A B C D

53. On a 4 Variables Karnaugh map
• One Cell requires 4 variables
• Two adjacent cells require 3 variables
• Four adjacent cells require 2 variables
• Eight adjacent cells require 1 variable
• Sixteen adjacent cells give a 1 or true

54. Simplify using Karnaugh map
First, we need to change the circuit to an SOP expression

55. Y= A + B + B C + ( A + B ) ( C + D)
Y = A B + B C + A B ( C + D )
Y = A B + B C + A B C + A B D
Y = A B + B C + A B C A B D
Y = A B + B C + (A + B + C ) ( A + B + D)
Y = A B + B C + A + A B + A D + B + B D + AC + C D
Simplify using Karnaugh map (cont’d)
comfirm back (the right answer)
SOP expression

56. Gray Code
00 A B
01 A B
11 A B
10 A B
00 01 11 10
C D C D C D C D
1 1
1 1
1 1 1 1
Y = 1
1 1 1 1
1 1
1 1
Simplify using Karnaugh map (cont’d)

57. K-Map POS Minimization

58. 3 Variables Karnaugh Map
Gray Code
0 0
0 1
1 1
1 0
0 1
AB
C
0 1
2 3
6 7
4 5

59. 3 Variables Karnaugh Map (cont’d)

60. 4 Variables Karnaugh Map
0 0
0 1
1 1
1 0
0 0 0 1 1 1 1 0
A B
C D
0 1 3 2
4 5 7 6
12 13 15 14
8 9 11 10

61. 4 Variables Karnaugh Map (cont’d)

62. 4 Variables Karnaugh Map (cont’d)

63. Mapping a Standard SOP expression
 Example:
Answer:
Mapping a Standard POS expression
 Example:
Using K-Map, convert the following standard POS
expression into a minimum SOP expression
Answer:
Y = AB + AC or standard SOP :
Karnaugh Map - Example
D
C
B
A
D
C
B
A
BCD
A
CD
B
A
D
C
B
A
D
C
B
A
Y 





CD
A
D
B
Y 

ABC
C
B
A
C
B
A
Y 


)
( C
B
A
Y 


64. K-Map with “Don’t Care” Conditions
Input Output
Example :
3 variables with output “don’t care (X)”

65. K-Map with “Don’t Care” Conditions (cont’d)
4 variables with output “don’t care (X)”

66. “Don’t Care” Conditions
 Example:
Determine the minimal SOP using K-Map:
Answer:
D
A
C
B
CD
D
C
B
A
F 


)
,
,
,
(
14,15)
D(5,12,13,
9,10)
M(0,2,6,8,
D)
C,
B,
F(A, 

K-Map with “Don’t Care” Conditions (cont’d)

67. Solution : 14,15)
D(5,12,13,
9,10)
M(0,2,6,8,
D)
C,
B,
F(A, 

D
A
C
B
CD
D
C
B
A
F 


)
,
,
,
(
AB
CD
00
01
11
10
00 01 11 10
0 1 1 0
1 X 1 0
X X X X
0 0 1 0
0 1 3 2
4 5 7 6
12 13 15 14
8 9 11 10
Minimum SOP expression is
CD
AD
BC

68. K-map Product of Sums simplification
Example: Simplify the Boolean function F(ABCD)=(0,1,2,5,8,9,10) in
(a) S-of-p (b) P-of-s
Using the minterms (1’s)
F(ABCD)= B’D’+B’C’+A’C’D
Using the maxterms (0’s) and complimenting F
Grouping as if they were minterms, then using De
Morgen’s theorem to get F.
F’(ABCD)= BD’+CD+AB
F(ABCD)= (B’+D)(C’+D’)(A’+B’)