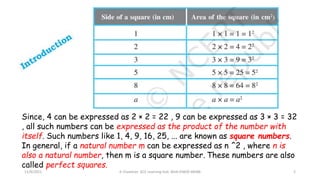
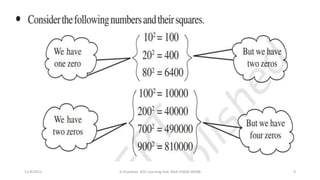
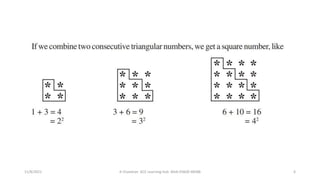
1) Square numbers are numbers that can be expressed as the product of a number multiplied by itself.
2) Between two consecutive square numbers n2 and (n+1)2, there are 2n non-square numbers.
3) The sum of the first n odd natural numbers is n2, meaning square numbers must be the sum of consecutive odd numbers starting from 1.