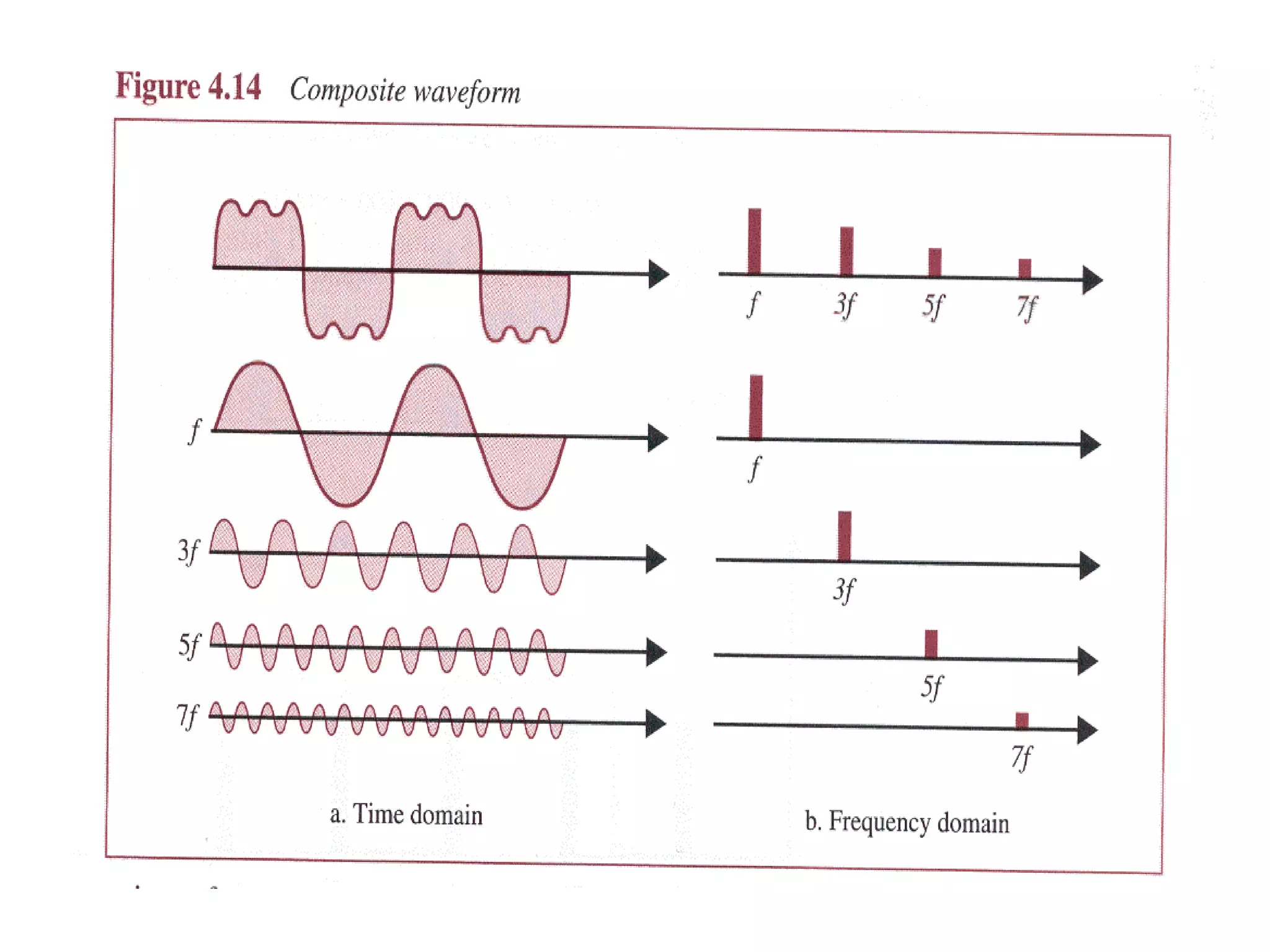
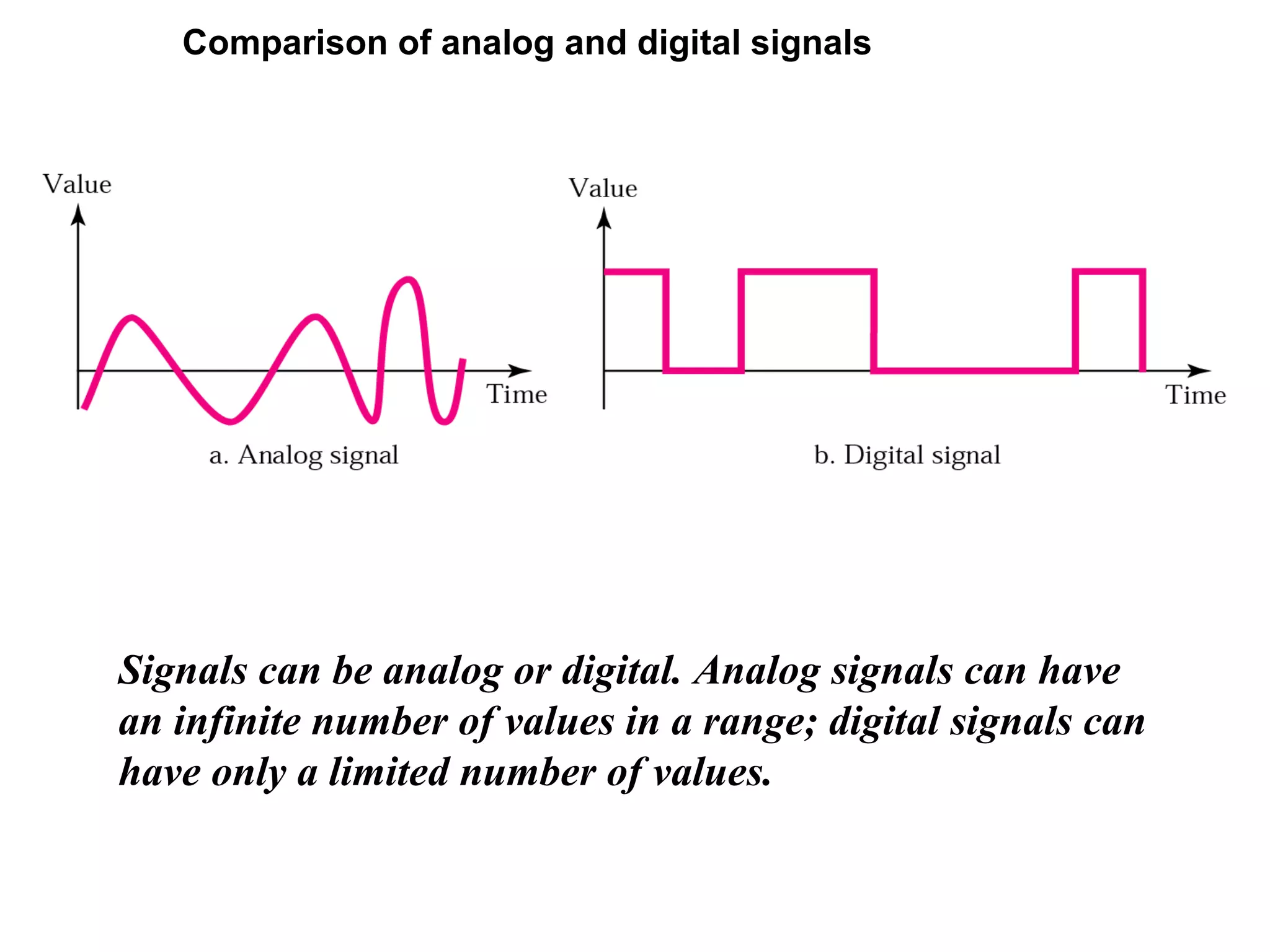
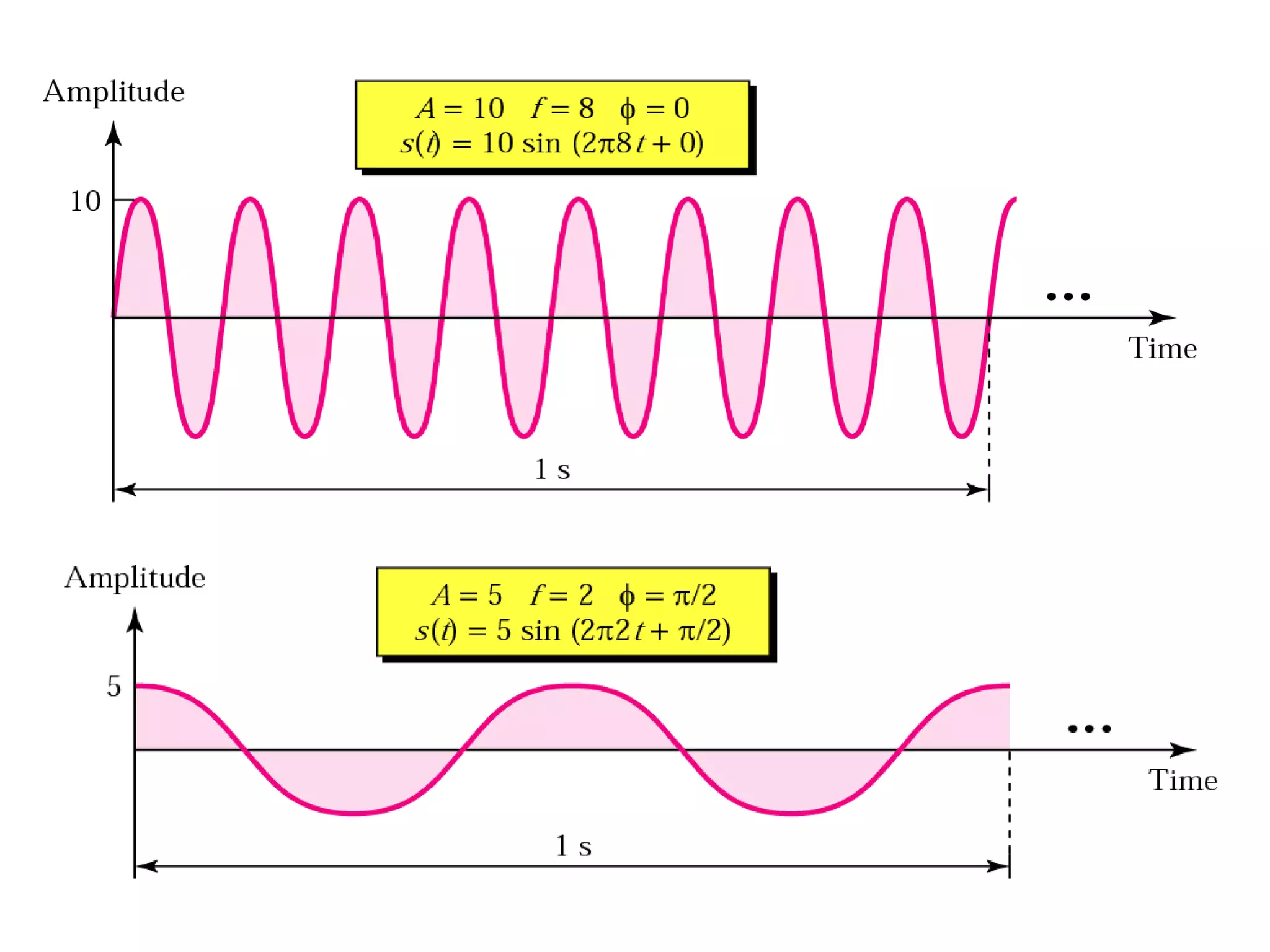
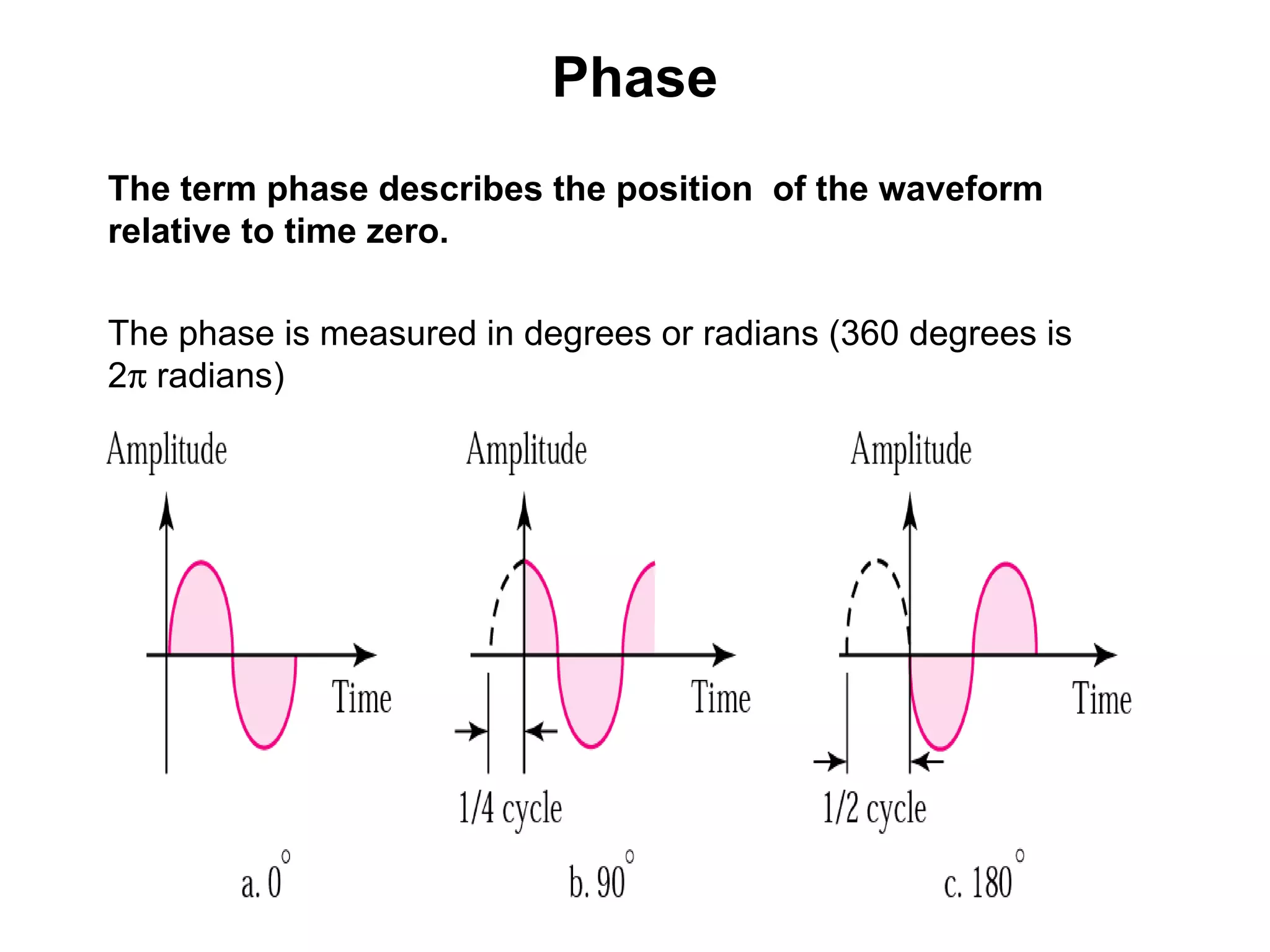
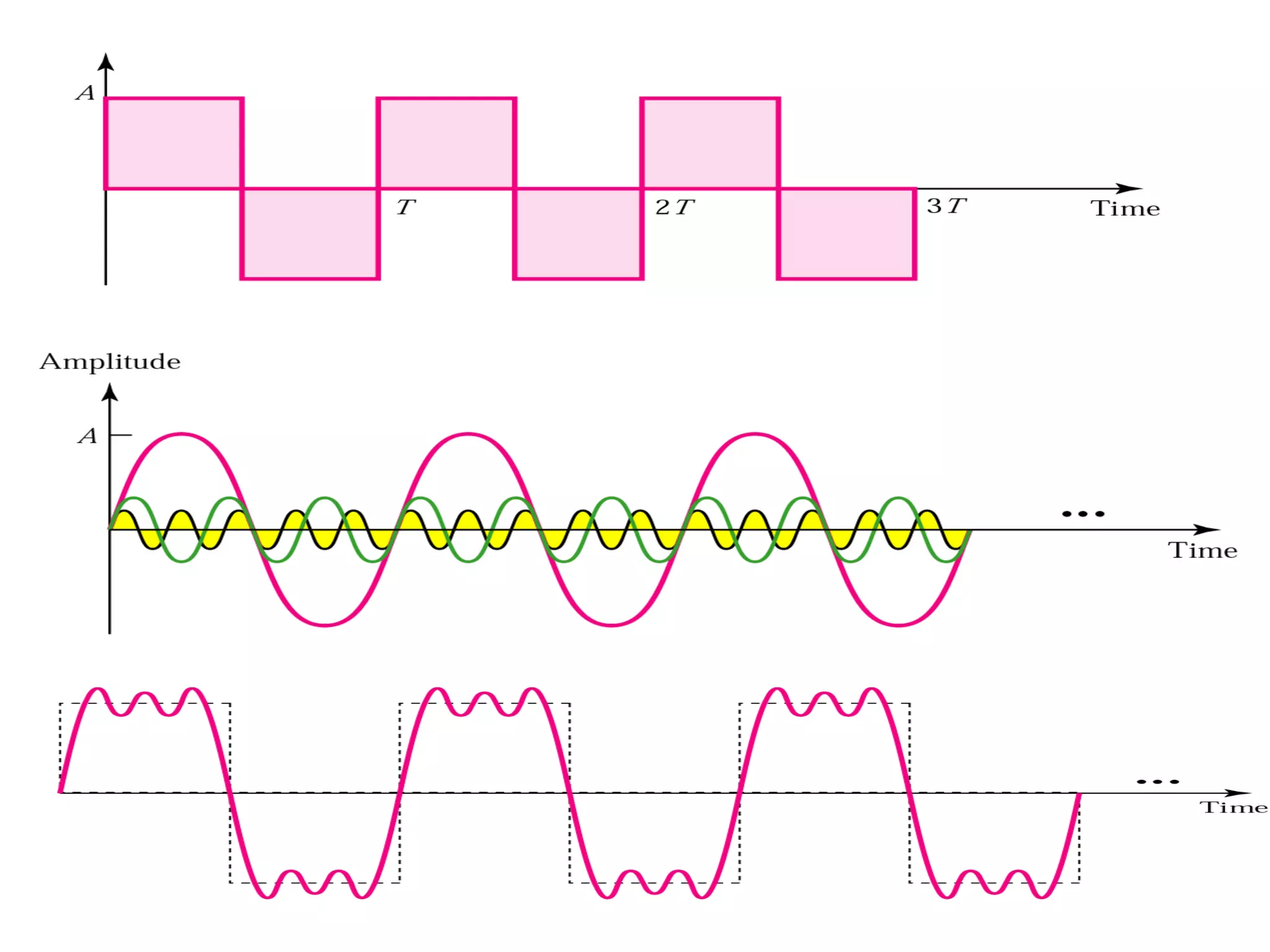
The document discusses various properties of signals including: - Analog signals can have an infinite number of values while digital signals are limited to a set of values. - Phase describes the position of a waveform relative to a reference point in time. - Total energy and average power of continuous and discrete signals can be calculated through integrals and sums. - Periodic, even, odd, exponential, and sinusoidal signals are described. 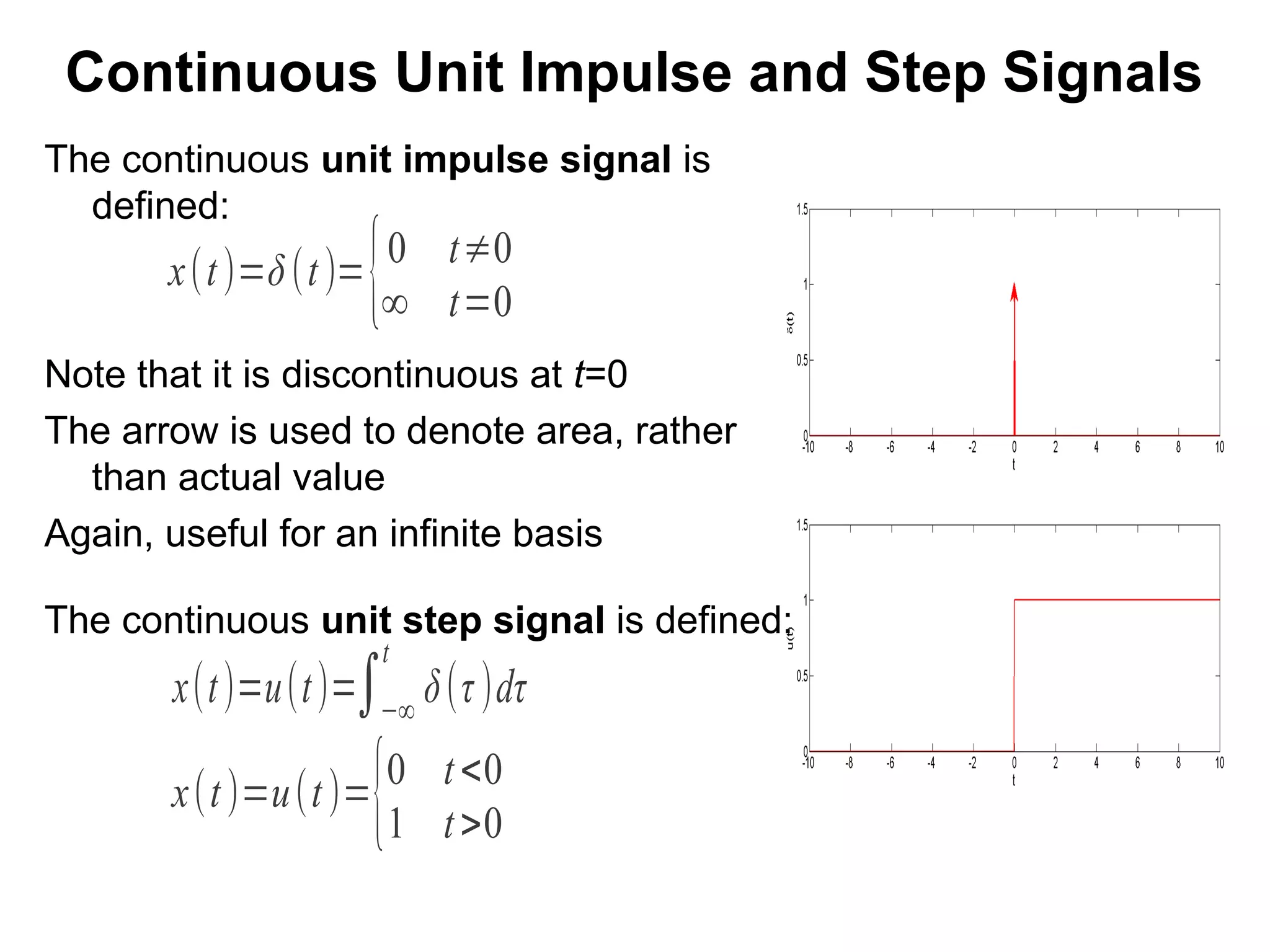- Unit impulse and step signals are defined for both discrete and continuous time domains. 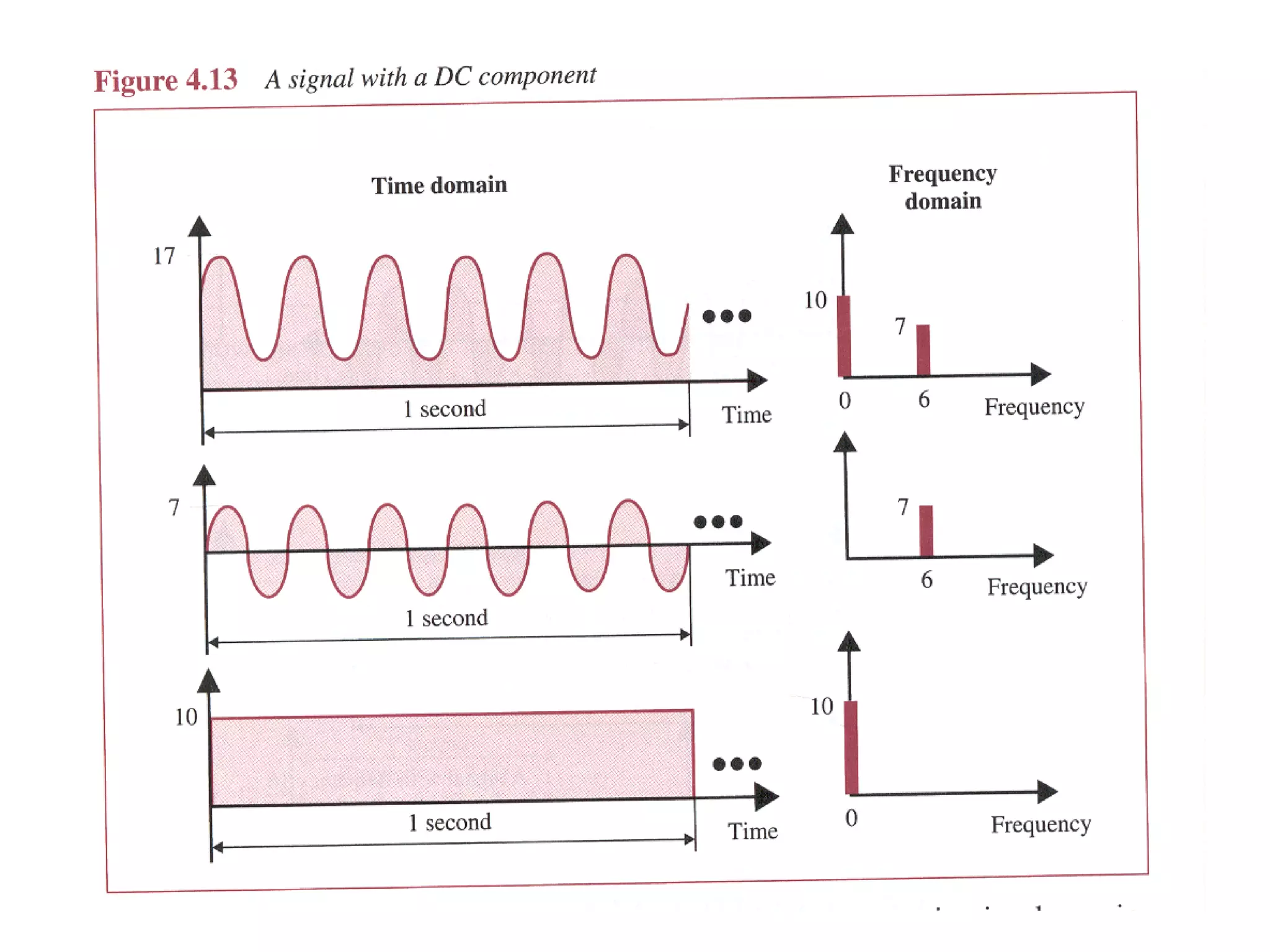- A signal's frequency spectrum shows the collection of component frequencies and bandwidth is the range of these frequencies.

1. Properties of Signals
Prof. Satheesh Monikandan.B
HOD-ECE
INDIAN NAVAL ACADEMY, EZHIMALA
sathy24@gmail.com
92 INAC-L-AT15

2. Comparison of analog and digital signals
Signals can be analog or digital. Analog signals can have
an infinite number of values in a range; digital signals can
have only a limited number of values.

3. Phase
The term phase describes the position of the waveform
relative to time zero.
The phase is measured in degrees or radians (360 degrees is
2π radians)

4. Signal Energy and Power
Total energy of a continuous signal x(t) over [t1, t2] is:
where |.| denote the magnitude of the (complex) number.
Similarly for a discrete time signal x[n] over [n1, n2]:
By dividing the quantities by (t2-t1) and (n2-n1+1), respectively,
gives the average power, P
Note that these are similar to the electrical analogies
(voltage), but they are different, both value and dimension.
E=∫t1
t2
∣x(t)∣2
dt
E=∑n=n1
n2
∣x[n]∣2

5. Energy and Power over Infinite Time
For many signals, we’re interested in examining the power and energy
over an infinite time interval (-∞, ∞). These quantities are therefore
defined by:
If the sums or integrals do not converge, the energy of such a signal is
infinite.
Two important (sub)classes of signals
1. Finite total energy (and therefore zero average power)
2. Finite average power (and therefore infinite total energy)
E∞=limT→∞∫−T
T
∣x(t)∣
2
dt=∫−∞
∞
∣x(t)∣
2
dt
E∞=limN →∞ ∑n=−N
N
∣x[n ]∣
2
=∑n=−∞
∞
∣x[n]∣
2
P∞=limT →∞
1
2T
∫−T
T
∣x(t)∣
2
dt
P∞=limN →∞
1
2N+1
∑n=−N
N
∣x[n]∣
2

6. An important class of signals is the class of periodic
signals. A periodic signal is a continuous time signal
x(t), that has the property
where T>0, for all t.
Examples:
cos(t+2π) = cos(t)
sin(t+2π) = sin(t)
Both are periodic with period 2π
For a signal to be periodic, the relationship must hold for
all t.
Periodic Signals
x(t)=x(t+T )
2π

7. An even signal is identical to its time reversed signal, i.e. it
can be reflected in the origin and is equal to the original:
Examples:
x(t) = cos(t)
An odd signal is identical to its negated, time reversed
signal, i.e. it is equal to the negative reflected signal
Examples:
x(t) = sin(t)
x(t) = t
This is important because any signal can be expressed as
the sum of an odd signal and an even signal.
Odd and Even Signals
x(−t)=x(t)
x(−t)=−x(t)

8. Exponential and Sinusoidal Signals
Exponential and sinusoidal signals are characteristic of real-world
signals and also from a basis (a building block) for other
signals.
A generic complex exponential signal is of the form:
where C and a are, in general, complex numbers.
Real exponential signals
x(t)=Ce
at
a>0
C>0
a<0
C>0
Exponential growth Exponential decay

9. Periodic Complex Exponential &
Sinusoidal Signals
Consider when a is purely imaginary:
By Euler’s relationship, this can be expressed
as:
This is a periodic signals because:
when T=2π/ω0
A closely related signal is the sinusoidal
signal:
We can always use:
x(t)=Ce
jω0
t
e
jω0
t
=cos ω0t + j sinω0 t
e
jω0(t+T )
=cosω0(t +T )+ j sinω0(t+T )
=cosω0 t + j sinω0 t=e
jω0t
x(t)=cos (ω0t+φ) ω0=2πf 0
A cos(ω0 t +φ)=A ℜ(e
j(ω0t +φ)
)
A sin (ω0 t+φ)=A ℑ(e
j(ω0
t +φ)
)
T0 = 2π/ω0
cos(1)
T0 is the fundamental
time period
ω0 is the fundamental
frequency

10. Exponential & Sinusoidal Signal Properties
Periodic signals, in particular complex periodic
and sinusoidal signals, have infinite total
energy but finite average power.
Consider energy over one period:
Therefore:
Average power:
Useful to consider harmonic signals
Terminology is consistent with its use in music,
where each frequency is an integer multiple
of a fundamental frequency.
E period=∫0
T0
∣e
jω0
t
∣
2
dt
=∫0
T 0
1dt=T0
P period=
1
T0
E period=1
E∞=∞

11. General Complex Exponential Signals
So far, considered the real and periodic complex exponential
Now consider when C can be complex. Let us express C is polar form
and a in rectangular form:
So
Using Euler’s relation
These are damped sinusoids
C=∣C∣e jφ
a=r+ jω0
Ceat
=∣C∣e jφ
e
(r+ jω0
)t
=∣C∣e
rt
e
j( ω
0
+φ)t
Ceat
=∣C∣e jφ
e
(r+ jω0
)t
=∣C∣e
rt
cos((ω0+φ)t)+ j∣C∣e
rt
sin((ω0 +φ)t)

12. Discrete Unit Impulse and Step Signals
The discrete unit impulse signal is defined:
Useful as a basis for analyzing other signals
The discrete unit step signal is defined:
Note that the unit impulse is the first
difference (derivative) of the step signal
Similarly, the unit step is the running sum
(integral) of the unit impulse.
x[n]=δ[n]={0 n≠0
1 n=0
x[n]=u[ n]={0 n<0
1 n≥0
δ[n]=u[n]−u[n−1]

13. Continuous Unit Impulse and Step Signals
The continuous unit impulse signal is
defined:
Note that it is discontinuous at t=0
The arrow is used to denote area, rather
than actual value
Again, useful for an infinite basis
The continuous unit step signal is defined:
x(t)=δ(t)={0 t≠0
∞ t=0
x(t)=u(t)=∫−∞
t
δ(τ )dτ
x(t)=u(t)={0 t<0
1 t>0

14. TIME AND FREQUENCY DOMAINS
•Time-domain representation
•Frequency-domain representation

16. Time and frequency domains

17. Periodic Composite Signals
A single-frequency sine wave is not useful in data
communications; we need to change one or more of its
characteristics to make it useful.
According to Fourier analysis, any composite signal
can be represented as a combination of simple sine
waves with different frequencies, phases, and
amplitudes.

19. Frequency spectrum comparison

22. Frequency Spectrum and Bandwidth
The frequency spectrum of a signal is the collection of all
the component frequencies it contains and is shown using a
frequency-domain graph.
The bandwidth of a signal is the width of the frequency
spectrum, i.e., bandwidth refers to the range of component
frequencies.
To compute the bandwidth, subtract the lowest frequency
from the highest frequency of the range.

23. Example 1Example 1
If a periodic signal is decomposed into five sine waves
with frequencies of 100, 300, 500, 700, and 900 Hz,
what is the bandwidth? Draw the spectrum, assuming all
components have a maximum amplitude of 10 V.
SolutionSolution
B = fh − fl = 900 − 100 = 800 Hz
The spectrum has only five spikes, at 100, 300, 500, 700,
and 900 (see Figure 13.4 )

24. Example 1