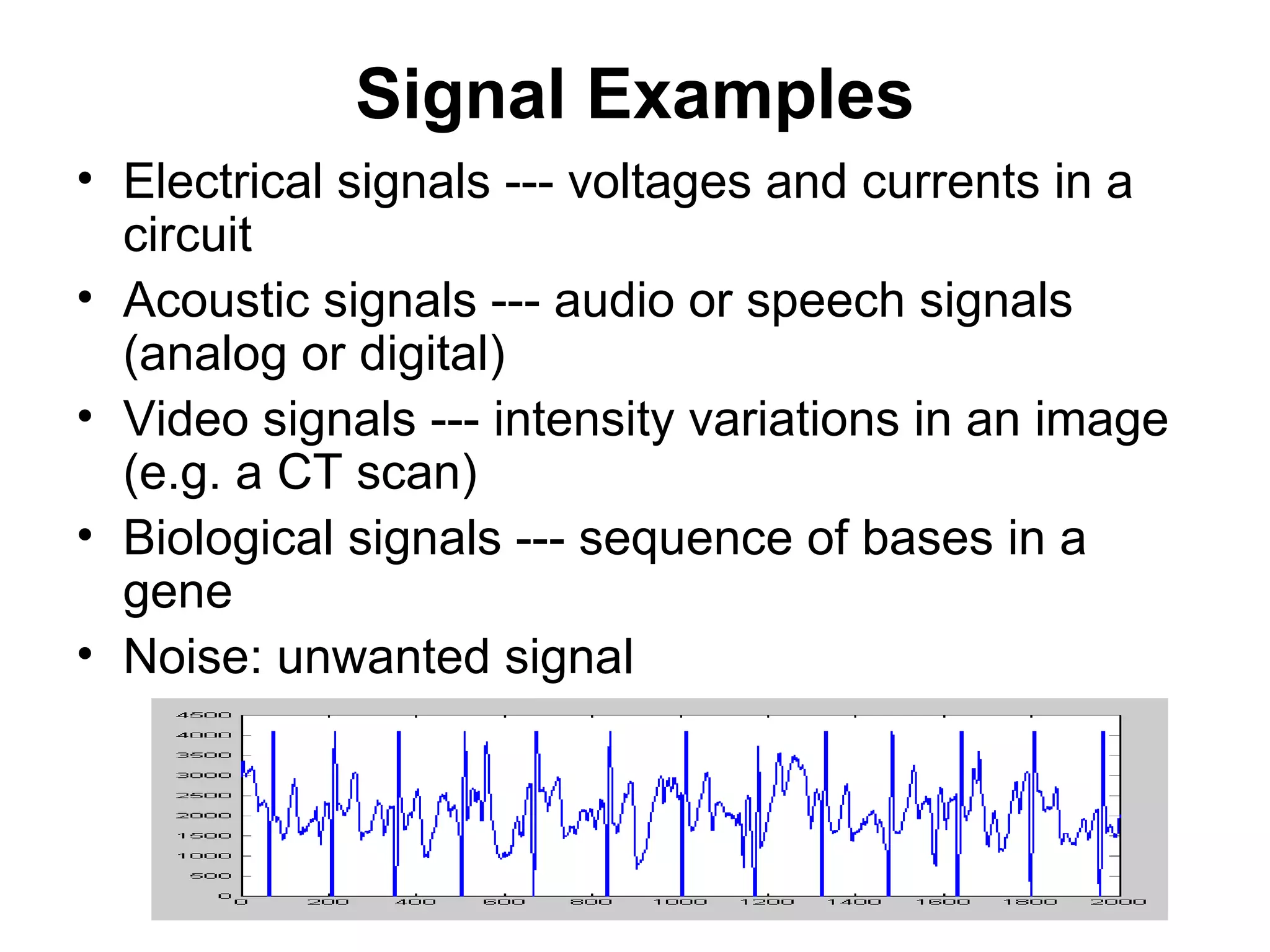
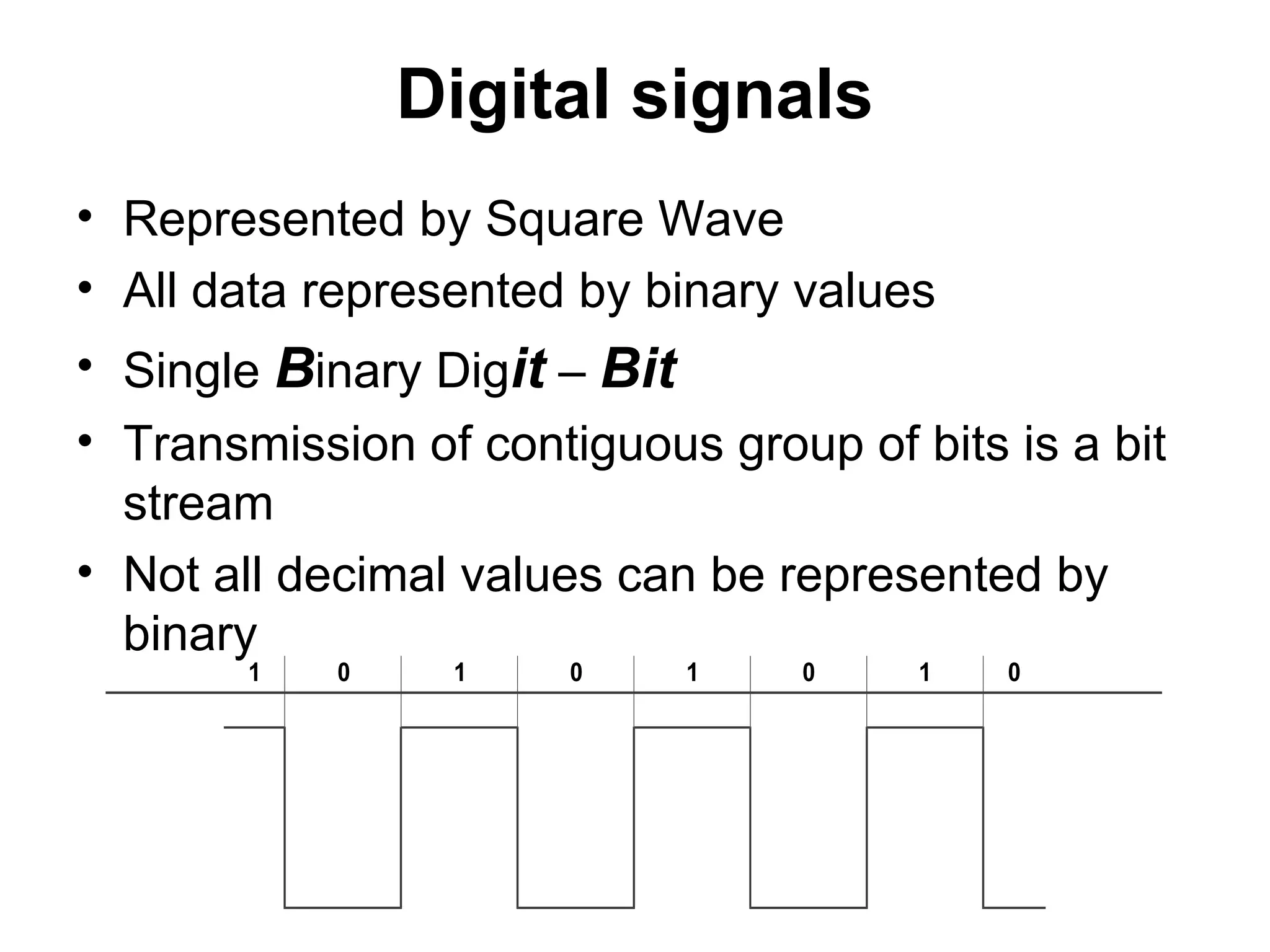
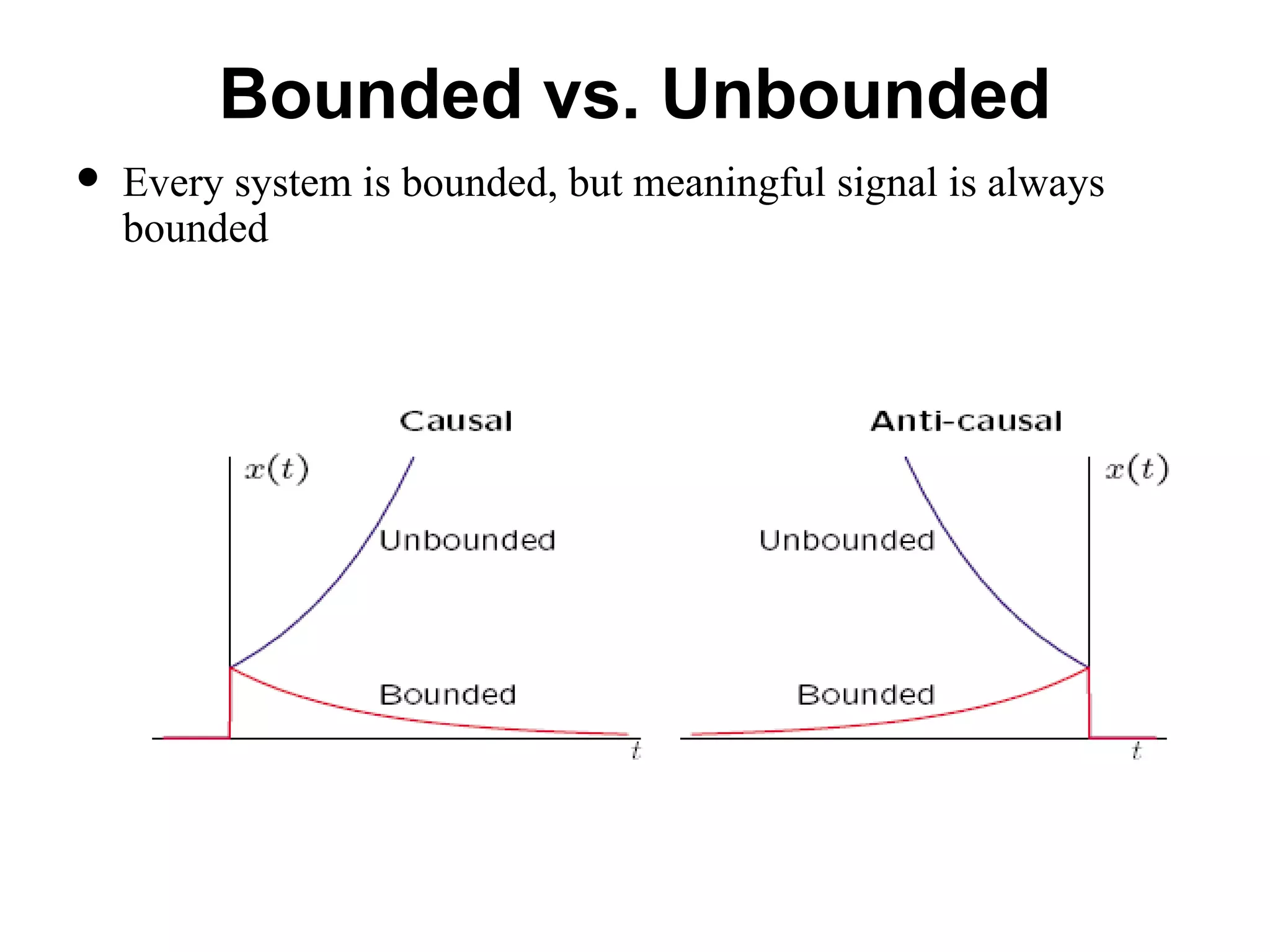
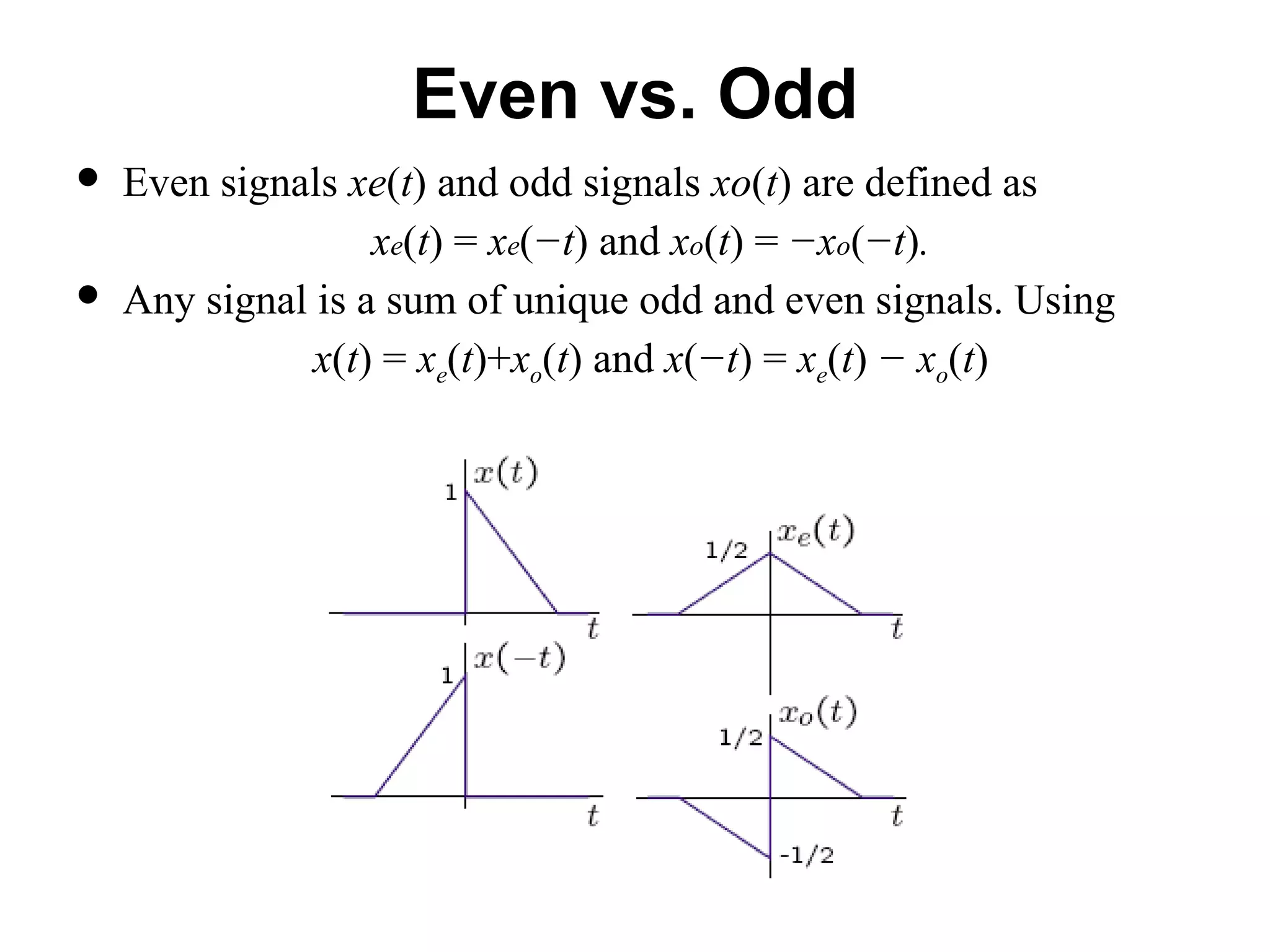
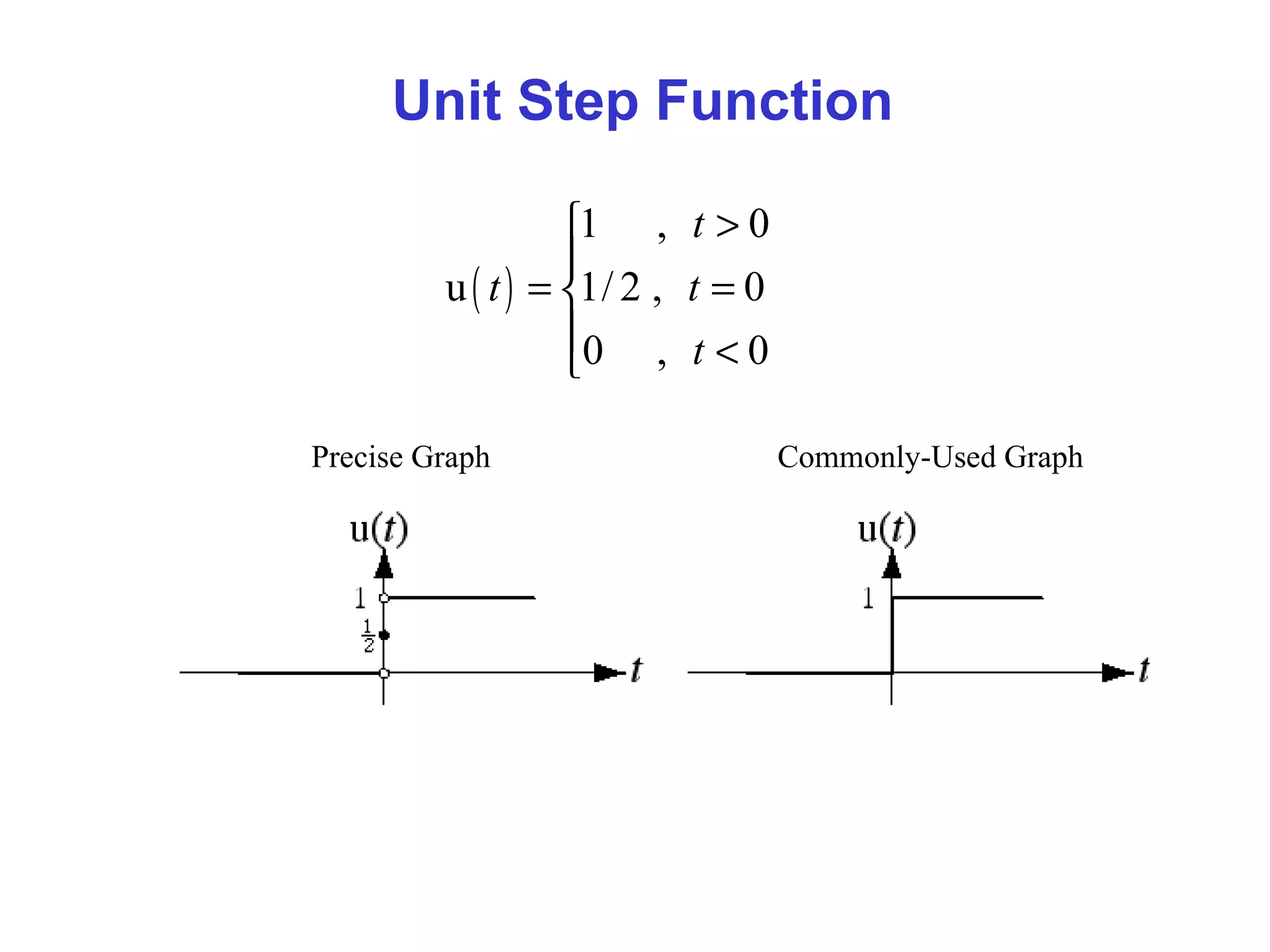
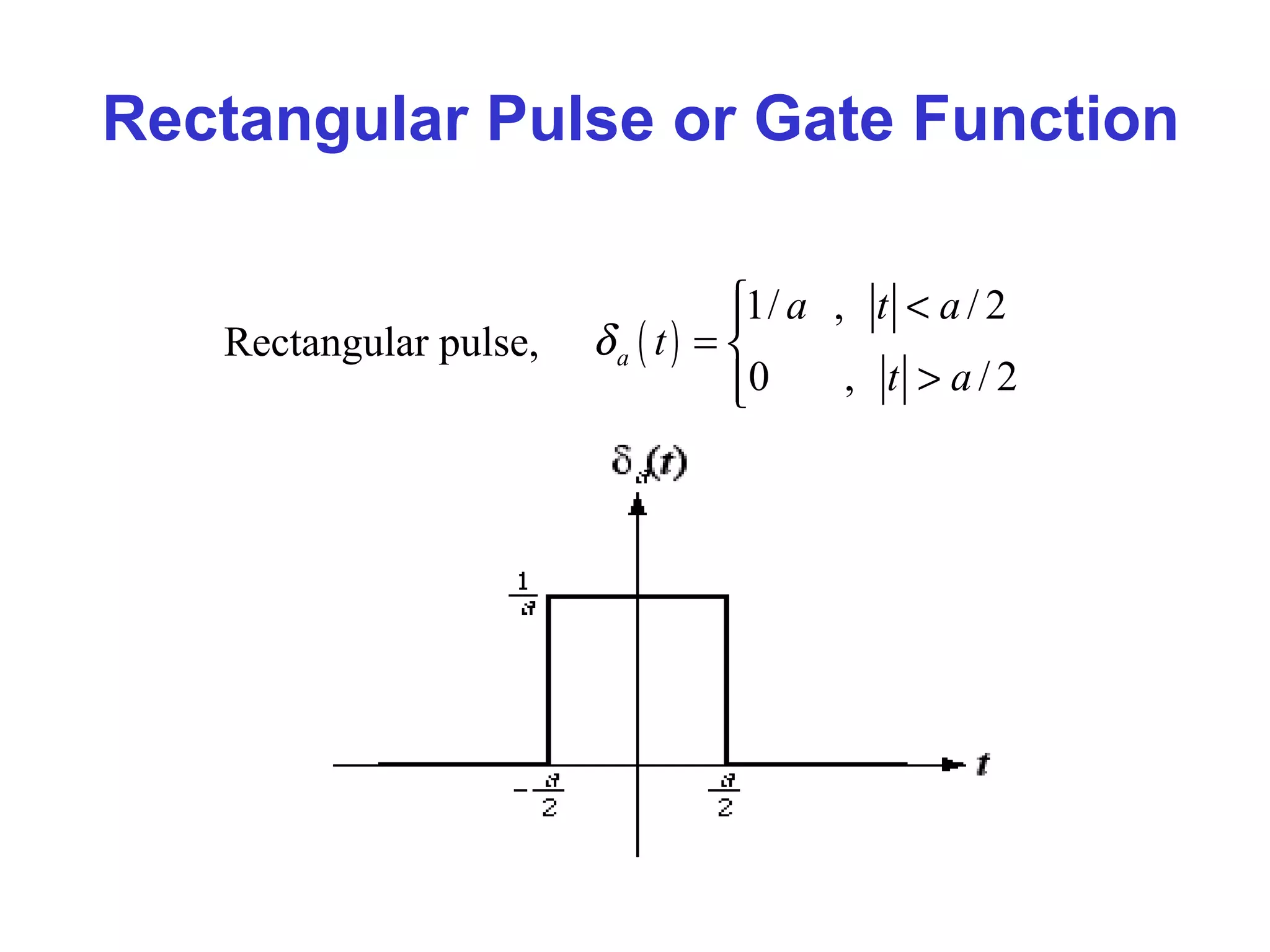
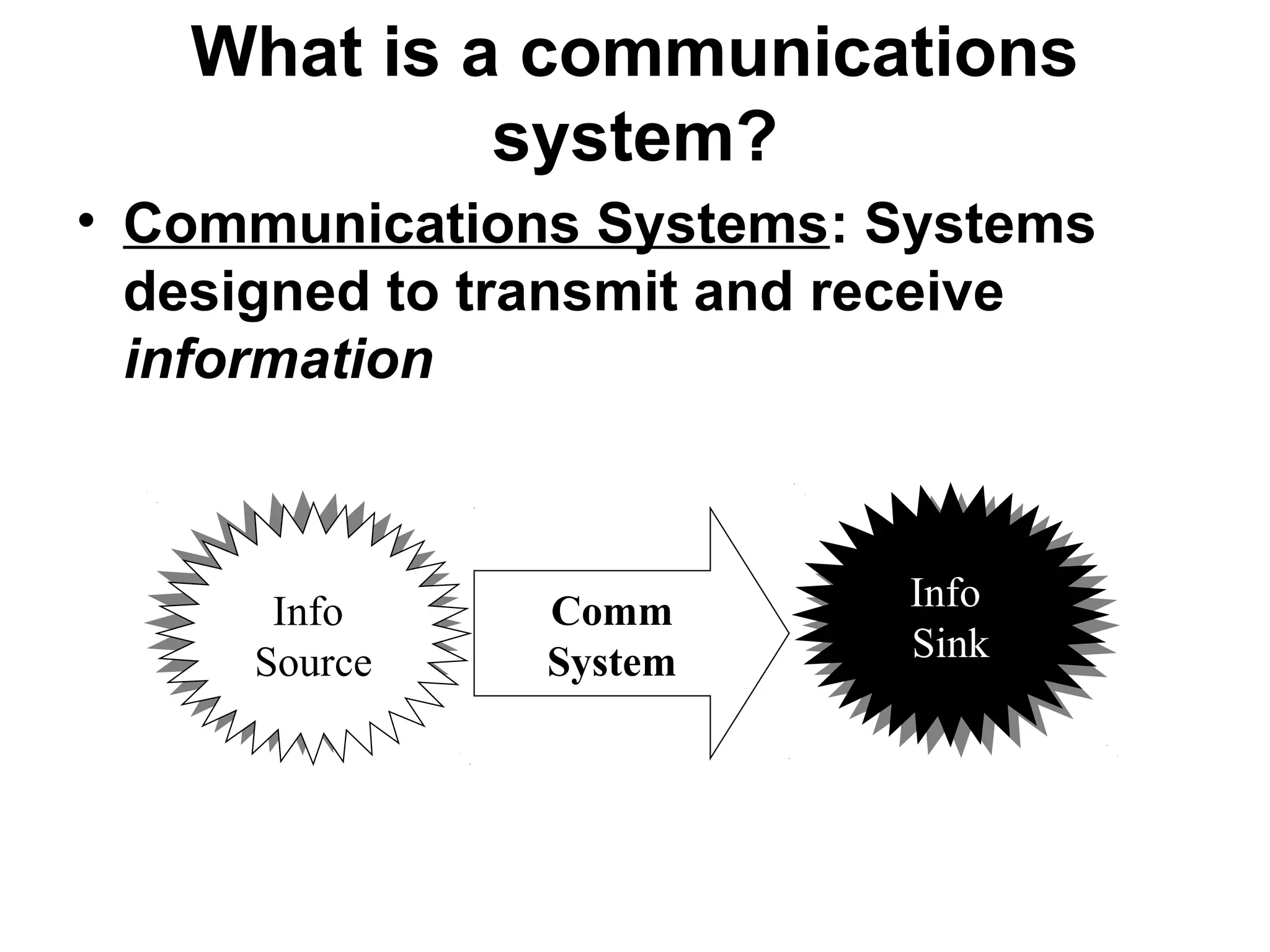
This document provides an overview of signals and systems. It begins with an introduction to signals, including definitions of key signal properties such as periodicity, causality, boundedness. It also distinguishes between continuous-time and discrete-time signals. The document then covers fundamental signal types including sinusoidal, exponential, unit step, and impulse signals. It concludes with discussions of signal processing concepts like the Fourier transform and basics of communication systems.

1. Signals and Systems
Prof. Satheesh Monikandan.B
HOD-ECE
INDIAN NAVAL ACADEMY, EZHIMALA
sathy24@gmail.com
92 INAC-L-AT15

2. • Course Code : ECL427
• Course title : SIGNALAS AND SYSTEMS
• Credit Hours : 3
• Semester : AT2015
• Refernece Book : A.V.Oppenheim, A.V.Willsky and
S.Hamid Nawab, “Signals and Systems,” PHI, 2nd
Edition, 2013.

3. Syllabus - I
• Introduction to Signals
• Spectral Analysis
– Fourier Series
– Fourier Transform
– Frequency Domain Representation of Finite Energy
Signals and Periodic Signals
– Signal Energy and Energy Spectral Density
– Signal Power and Power Spectral Density
• Signal Transmission through a Linear System
– Convolution Integral and Transfer Function

4. Outline
• Signals and Systems
– Signals and Systems
– What is a signal?
– Signal Basics
– Analog / Digital Signals
– Real vs Complex
– Periodic vs. Aperiodic
– Bounded vs. Unbounded
– Causal vs. Noncausal
– Even vs. Odd
– Power vs. Energy

5. CAUSAL AND NON-CAUSAL
SIGNALS

8. CASUAL AND NON-CAUSAL
SYSTEM

10. The Bands
VLF LF MF HF VHF UHF SHF EHF
Submillimeter
Range
ELF
3MHz 30MHz300MHz 3GHz 30GHz 300GHz
Far
Infra-
Red
300KHz30KHz 3THz
300m
Radio Optical
3KHz
Near
Infra-
Red
700nm
1PetaHz
R
e
d
O
r
a
n
g
e
Y
e
l
l
o
w
G
r
e
e
n
B
l
u
e
I
n
d
i
g
o
V
i
o
l
e
t
600nm 400nm500nm
Ultraviolet
1ExaHz
X-Ray
1500nm

11. Introduction to Signals
• A Signal is the function of one or more independent
variables that carries some information to represent
a physical phenomenon.
• A continuous-time signal, also called an analog
signal, is defined along a continuum of time.

12. A discrete-time signal is defined at
discrete times.

14. Elementary Signals
Sinusoidal & Exponential Signals
• Sinusoids and exponentials are important in signal
and system analysis because they arise naturally in
the solutions of the differential equations.
• Sinusoidal Signals can expressed in either of two
ways :
cyclic frequency form- A sin 2Пfot = A sin(2П/To)t
radian frequency form- A sin ωot
ωo = 2Пfo = 2П/To
To = Time Period of the Sinusoidal Wave

15. Sinusoidal & Exponential Signals Contd.
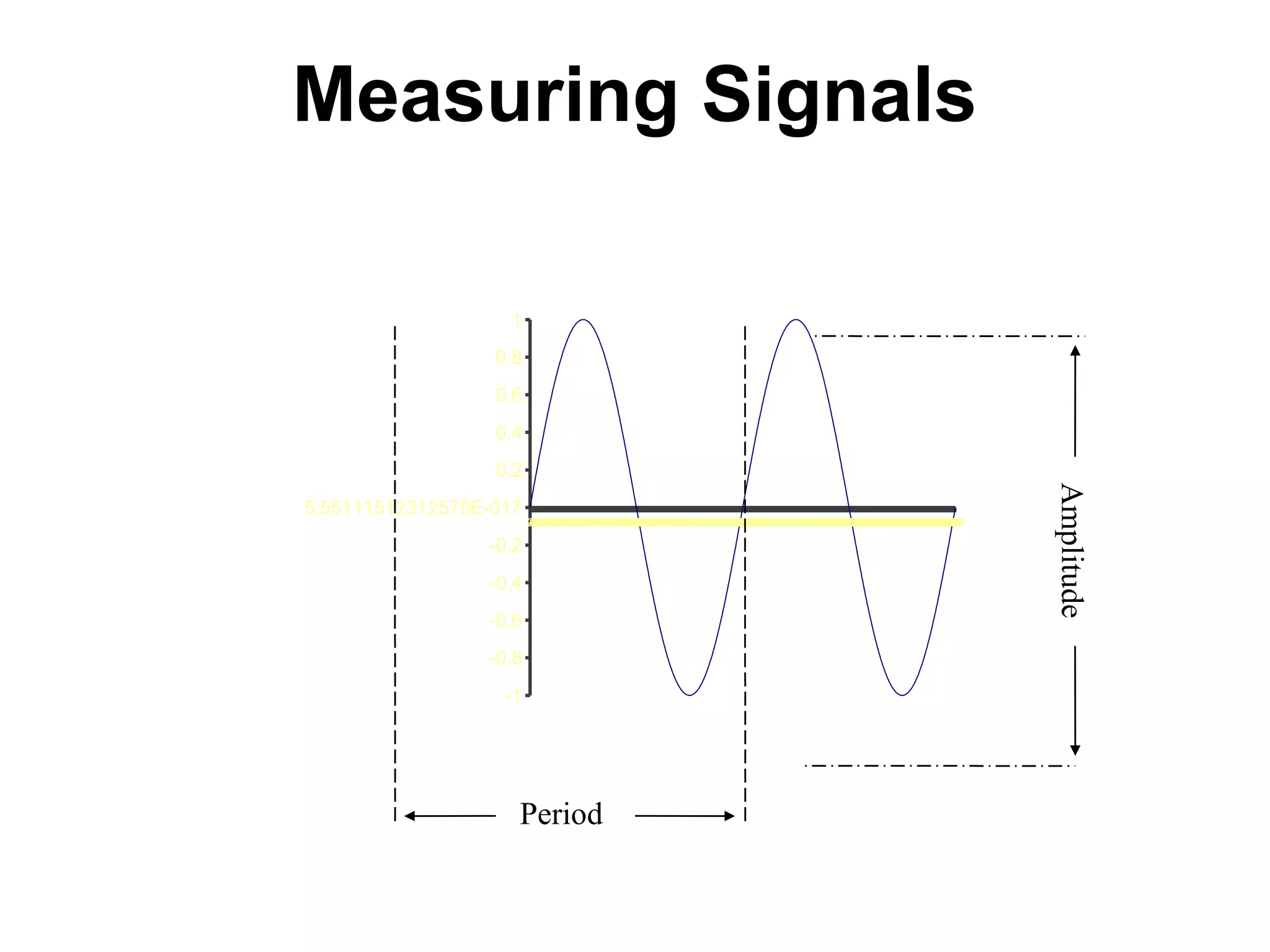
x(t) = A sin (2Пfot+ θ)
= A sin (ωot+ θ)
x(t) = Aeat Real Exponential
= Aejω̥t =
A[cos (ωot) +j sin (ωot)] Complex Exponential
θ = Phase of sinusoidal wave
A = amplitude of a sinusoidal or exponential signal
fo = fundamental cyclic frequency of sinusoidal signal
ωo = radian frequency
Sinusoidal signal

16. Signal Examples
• Electrical signals --- voltages and currents in a
circuit
• Acoustic signals --- audio or speech signals
(analog or digital)
• Video signals --- intensity variations in an image
(e.g. a CT scan)
• Biological signals --- sequence of bases in a
gene
• Noise: unwanted signal
:

17. Measuring Signals
2468101214161820222426283032343638404244464850525456586062646668707274767880828486889092949698100102104106108110112114116118120122124126128130132134136138140142144146148150152154156158160162164166168170172174176178180182184186188190192194196198200202204206208210212214216218220222224226228230232234236238240242244246248250252254256258260262264266268270272274276278280282284286288290292294296298300302304306308310312314316318320322324326328330332334336338340342344346348350352354356358360362364366368370372374376378380382384386388390392394396398400402404406408410412414416418420422424426428430432434436438440442444446448450452454456458460462464466468470472474476478480482484486488490492494496498500502504506508510512514516518520522524526528530532534536538540542544546548550552554556558560562564566568570572574576578580582584586588590592594596598600602604606608610612614616618620622624626628630632634636638640642644646648650652654656658660662664666668670672674676678680682684686688690692694696698700702704706708710712714716718720
-1
-0.8
-0.6
-0.4
-0.2
5.55111512312578E-017
0.2
0.4
0.6
0.8
1
Period
Amplitude

18. Definitions
• Voltage – the force which moves an electrical current
against resistance
• Waveform – the shape of the signal (previous slide is a
sine wave) derived from its amplitude and frequency
over a fixed time (other waveform is the square wave)
• Amplitude – the maximum value of a signal, measured
from its average state
• Frequency (pitch) – the number of cycles produced in a
second – Hertz (Hz). Relate this to the speed of a
processor eg 1.4GigaHertz or 1.4 billion cycles per
second

19. Signal Basics
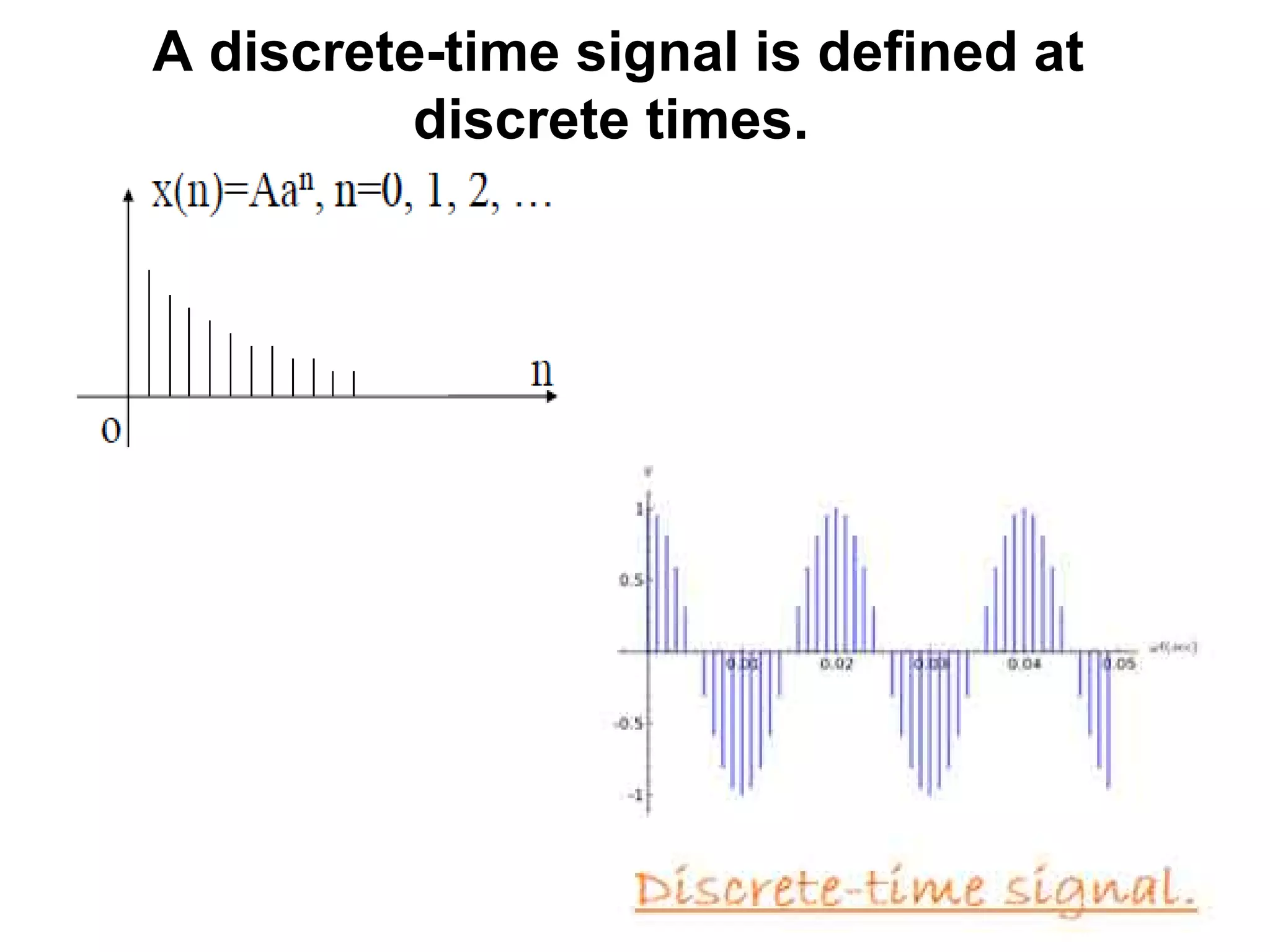
 Continuous time (CT) and discrete time (DT) signals
CT signals take on real or complex values as a function of an independent
variable that ranges over the real numbers and are denoted as x(t).
DT signals take on real or complex values as a function of an independent
variable that ranges over the integers and are denoted as x[n].
Note the subtle use of parentheses and square brackets to distinguish between
CT and DT signals.

20. Analog Signals
• Human Voice – best example
• Ear recognises sounds 20KHz or less
• AM Radio – 535KHz to 1605KHz
• FM Radio – 88MHz to 108MHz

21. Digital signals
• Represented by Square Wave
• All data represented by binary values
• Single Binary Digit – Bit
• Transmission of contiguous group of bits is a bit
stream
• Not all decimal values can be represented by
binary
1 0 1 0 1 0 1 0

22. Analogue vs. Digital
Analogue Advantages
• Best suited for audio and video
• Consume less bandwidth
• Available world wide
Digital Advantages
• Best for computer data
• Can be easily compressed
• Can be encrypted
• Equipment is more common and less expensive
• Can provide better clarity

23. Analog or Digital
• Analog Message: continuous in amplitude and over
time
– AM, FM for voice sound
– Traditional TV for analog video
– First generation cellular phone (analog mode)
– Record player
• Digital message: 0 or 1, or discrete value
– VCD, DVD
– 2G/3G cellular phone
– Data on your disk

24. A/D and D/A
• Analog to Digital conversion; Digital to
Analog conversion
– Gateway from the communication device to the
channel
• Nyquist Sampling theorem
– From time domain: If the highest frequency in the
signal is B Hz, the signal can be reconstructed
from its samples, taken at a rate not less than 2B
samples per second

25. Real vs. Complex
Q. Why do we deal with complex signals?
A. They are often analytically simpler to deal with than real
signals, especially in digital communications.

26. Periodic vs. Aperiodic Signals
 Periodic signals have the property that x(t + T) = x(t) for all t.
 The smallest value of T that satisfies the definition is called the
period.
 Shown below are an aperiodic signal (left) and a periodic signal
(right).

27.  A causal signal is zero for t < 0 and an non-causal signal is
zero for t > 0
 Right- and left-sided signals
A right-sided signal is zero for t < T and a left-sided signal is zero
for t > T where T can be positive or negative.
Causal vs. Non-causal

28. Bounded vs. Unbounded
 Every system is bounded, but meaningful signal is always
bounded

29. Even vs. Odd
 Even signals xe(t) and odd signals xo(t) are defined as
xe(t) = xe(−t) and xo(t) = −xo(−t).
 Any signal is a sum of unique odd and even signals. Using
x(t) = xe(t)+xo(t) and x(−t) = xe(t) − xo(t)

30. Another Classification of Signals
(Waveforms)
• Deterministic Signals: Can be modeled as a
completely specified function of time
• Random or Stochastic Signals: Cannot be
completely specified as a function of time; must be
modeled probabilistically

31. Unit Step Function
( )
1 , 0
u 1/ 2 , 0
0 , 0
t
t t
t
>

= =
 <
Precise Graph Commonly-Used Graph

32. Signum Function
( ) ( )
1 , 0
sgn 0 , 0 2u 1
1 , 0
t
t t t
t
> 
 
= = = − 
 − < 
Precise Graph Commonly-Used Graph
The signum function, is closely related to the unit-step
function.

33. Unit Ramp Function
( ) ( ) ( )
, 0
ramp u u
0 , 0
t
t t
t d t t
t
λ λ
−∞
> 
= = = 
≤ 
∫
•The unit ramp function is the integral of the unit step function.
•It is called the unit ramp function because for positive t, its
slope is one amplitude unit per time.

34. Rectangular Pulse or Gate Function
Rectangular pulse, ( )
1/ , / 2
0 , / 2
a
a t a
t
t a
δ
 <
= 
>

35. Representation of Impulse
Function
The area under an impulse is called its strength or weight. It is
represented graphically by a vertical arrow. An impulse with a
strength of one is called a unit impulse.

36. Properties of the Impulse Function
( ) ( ) ( )0 0g gt t t dt tδ
∞
−∞
− =∫
The Sampling Property
( )( ) ( )0 0
1
a t t t t
a
δ δ− = −
The Scaling Property
The Replication Property
g(t)⊗ δ(t) = g (t)

37. Unit Impulse Train
The unit impulse train is a sum of infinitely uniformly-
spaced impulses and is given by
( ) ( ) , an integerT
n
t t nT nδ δ
∞
=−∞
= −∑

38. The Unit Rectangle Function
The unit rectangle or gate signal can be represented as combination
of two shifted unit step signals as shown

39. The Unit Triangle Function
A triangular pulse whose height and area are both one but its base
width is not, is called unit triangle function. The unit triangle is
related to the unit rectangle through an operation called
convolution.

40. Sinc Function
( )
( )sin
sinc
t
t
t
π
π
=

41. Signal Properties: Terminology
• Waveform
• Time-average operator
• Periodicity
• DC value
• Power
• RMS Value
• Normalized Power
• Normalized Energy

42. Power and Energy Signals
• Power Signal
– Infinite duration
– Normalized power
is finite and non-
zero
– Normalized energy
averaged over
infinite time is
infinite
– Mathematically
tractable
• Energy Signal
– Finite duration
– Normalized energy
is finite and non-
zero
– Normalized power
averaged over
infinite time is zero
– Physically
realizable

43. The Decibel (dB)
• Measure of power transfer
• 1 dB = 10 log10 (Pout / Pin)
• 1 dBm = 10 log10 (P / 10-3
) where P is in Watts
• 1 dBmV = 20 log10 (V / 10-3
) where V is in Volts

44. What is a communications
system?
• Communications Systems: Systems
designed to transmit and receive
information
Info
Source
Info
Source
Info
Sink
Info
Sink
Comm
System

45. Block Diagram
Receiver
Rx
received
message
to
sink
̃m(t)
Transmitter
Tx s(t)
transmitted
signal
Channel
r(t)
received
signal
m(t)
message
from
source
Info
Source
Info
Source
Info
Sink
Info
Sink
n(t)
noise

46. Telecommunication
• Telegraph
• Fixed line telephone
• Cable
• Wired networks
• Internet
• Fiber communications
• Communication bus inside computers to
communicate between CPU and memory

47. Wireless Communications
• Satellite
• TV
• Cordless phone
• Cellular phone
• Wireless LAN, WIFI
• Wireless MAN, WIMAX
• Bluetooth
• Ultra Wide Band
• Wireless Laser
• Microwave
• GPS
• Ad hoc/Sensor Networks

48. Comm. Sys. Bock Diagram
̃m(t)Tx
s(t)
Channel
r(t)
m(t)
Noise
Rx
Baseband
Signal
Baseband
Signal
Bandpass
Signal• “Low” Frequencies
• <20 kHz
• Original data rate
• “High” Frequencies
• >300 kHz
• Transmission data rate
Modulation
Demodulation
or
Detection

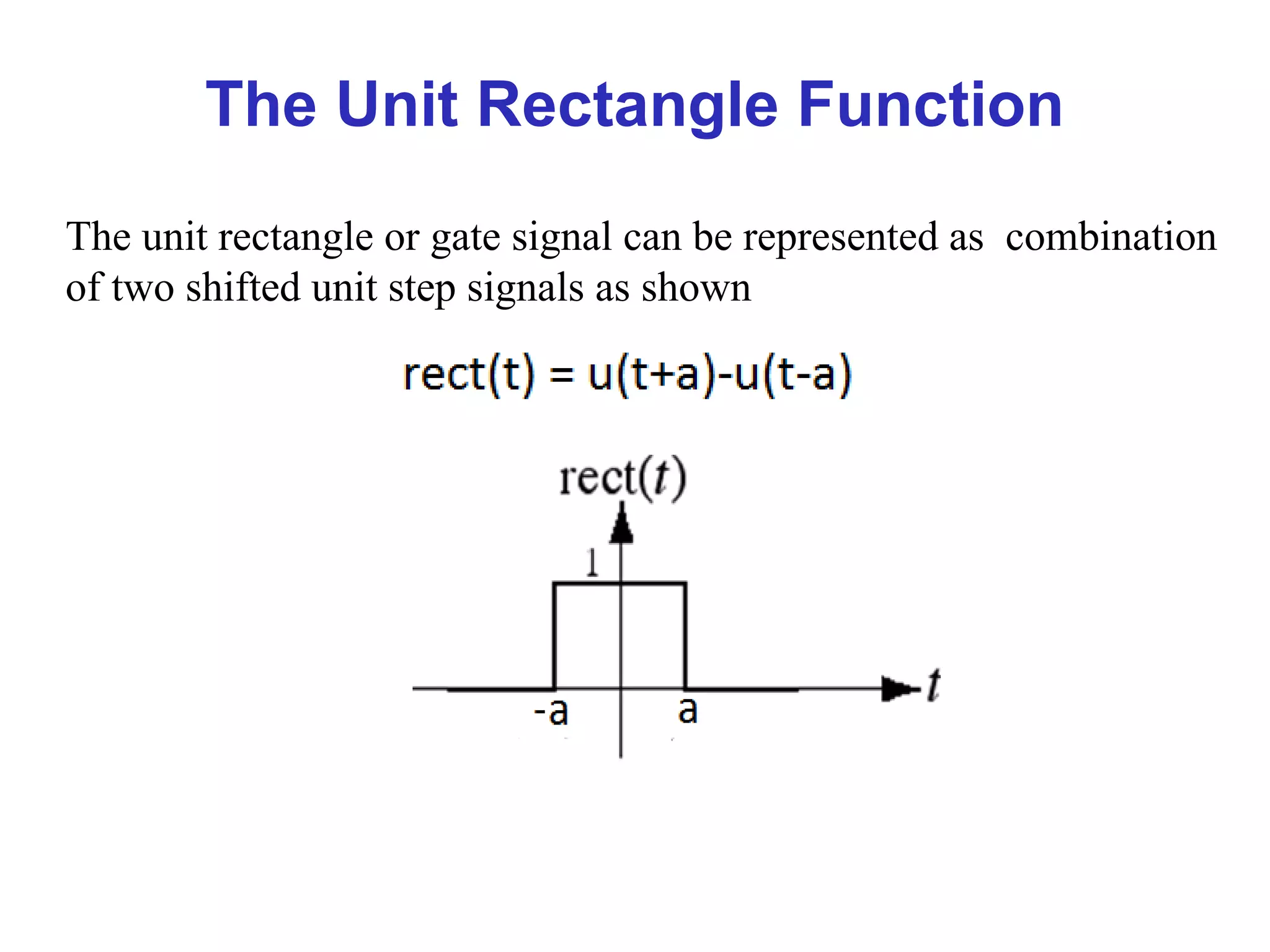
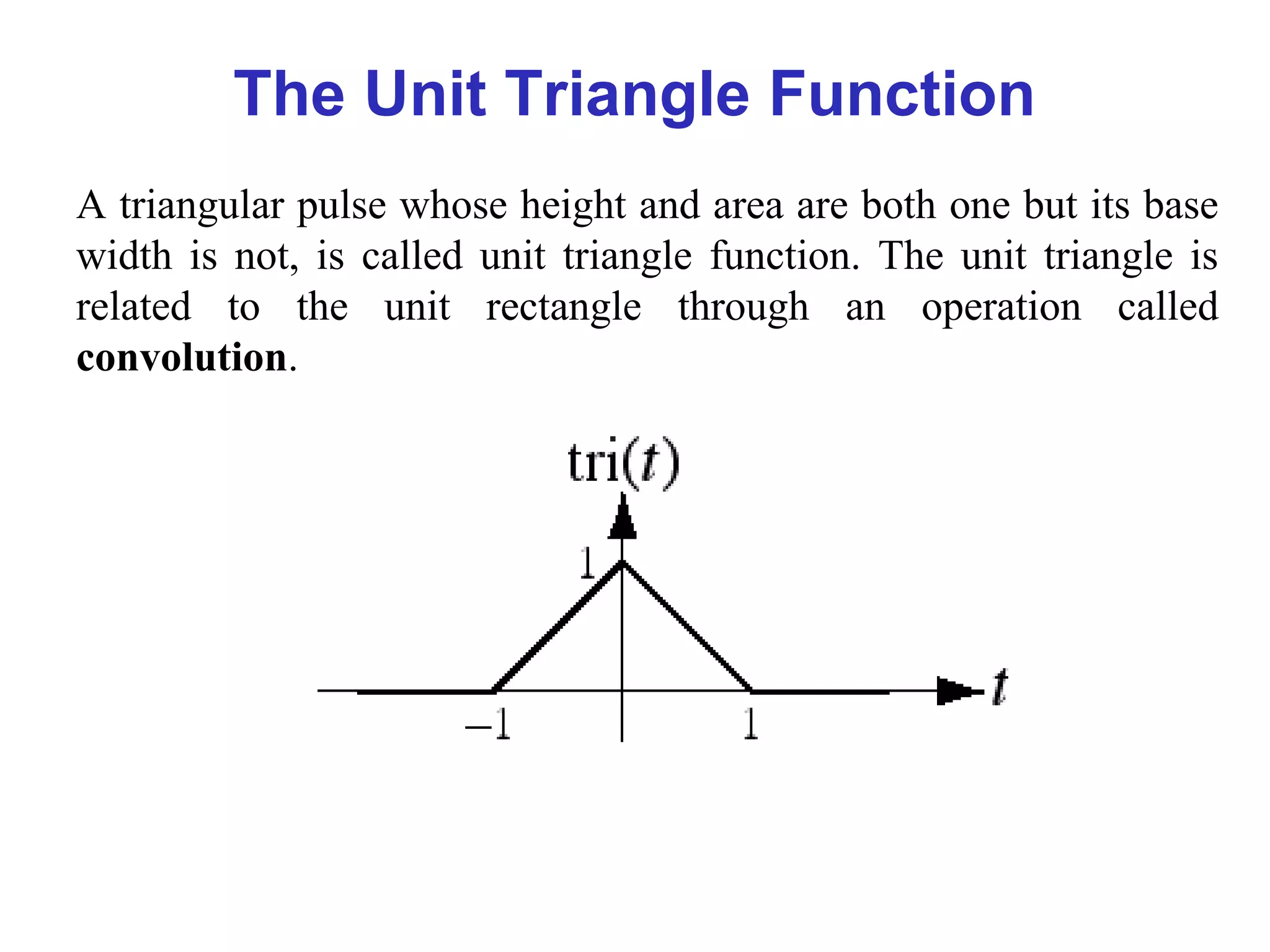
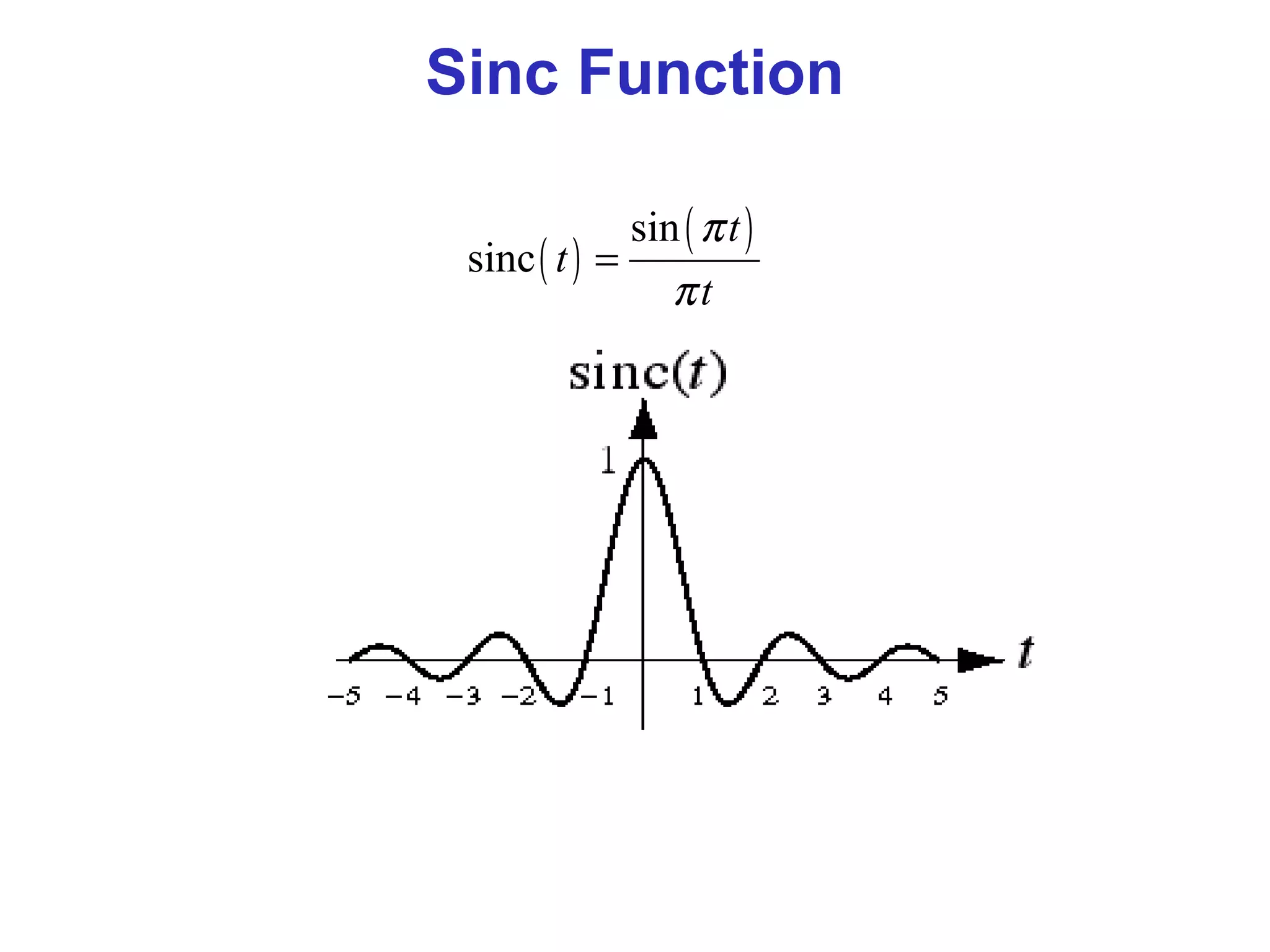
49. Discrete-Time Signals
• Sampling is the acquisition of the values of a
continuous-time signal at discrete points in time
• x(t) is a continuous-time signal, x[n] is a
discrete-time signal
[ ] ( )x x where is the time between sampless sn nT T=

50. Discrete Time Exponential and
Sinusoidal Signals
• DT signals can be defined in a manner analogous to
their continuous-time counter part
x[n] = A sin (2Пn/No+θ)
= A sin (2ПFon+ θ)
x[n] = an
n = the discrete time
A = amplitude
θ = phase shifting radians,
No = Discrete Period of the wave
1/N0 = Fo = Ωo/2 П = Discrete Frequency
Discrete Time Sinusoidal
Signal
Discrete Time Exponential
Signal

51. Discrete Time Sinusoidal
Signals

52. Discrete Time Unit Step Function
or Unit Sequence Function
[ ]
1 , 0
u
0 , 0
n
n
n
≥
= 
<

53. Discrete Time Unit Ramp
Function
[ ] [ ]
, 0
ramp u 1
0 , 0
n
m
n n
n m
n =−∞
≥ 
= = − 
< 
∑

54. Discrete Time Unit Impulse
Function or Unit Pulse Sequence
[ ]
1 , 0
0 , 0
n
n
n
δ
=
= 
≠
[ ] [ ] for any non-zero, finite integer .n an aδ δ=

55. Operations of Signals
• Sometime a given mathematical function may
completely describe a signal .
• Different operations are required for different
purposes of arbitrary signals.
• The operations on signals can be
Time Shifting
Time Scaling
Time Inversion or Time Folding

56. Time Shifting
• The original signal x(t) is shifted by an
amount tₒ.
• X(t)X(t-to) Signal Delayed Shift to the
right

57. Time Shifting Contd.
• X(t)X(t+to) Signal Advanced
Shift to the left