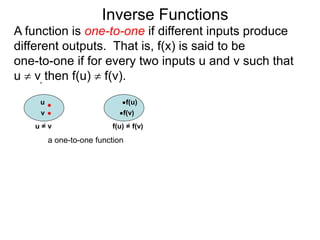
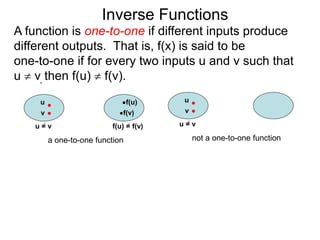
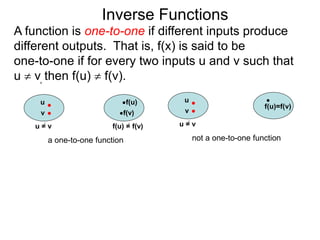
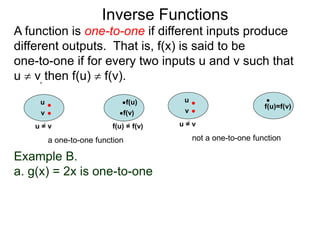
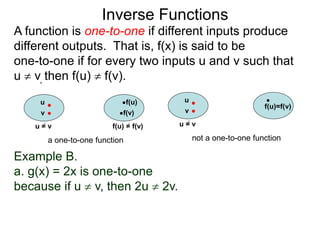
The document discusses inverse functions. An inverse function reverses the input and output of a function. For a function f(x) to have an inverse function f-1(y), it must be one-to-one, meaning that different inputs produce different outputs. The inverse of a function f(x) is found by solving the original function equation for x in terms of y. Examples show finding the inverse of specific functions like f(x) = x - 5 by solving for x. A function is one-to-one if for any two different inputs u and v, their outputs f(u) and f(v) are also different.

1. Inverse Functions

2. A function f(x) = y takes an input x and produces
one output y.
Inverse Functions

3. A function f(x) = y takes an input x and produces
one output y. Often we represent a function by the
following figure.
Inverse Functions
domian rangex y=f(x)
f

4. A function f(x) = y takes an input x and produces
one output y. Often we represent a function by the
following figure.
Inverse Functions
We like to reverse the operation, i.e., if we know
the output y, what was (were) the input x?
domian rangex y=f(x)
f

5. A function f(x) = y takes an input x and produces
one output y. Often we represent a function by the
following figure.
Inverse Functions
We like to reverse the operation, i.e., if we know
the output y, what was (were) the input x?
This procedure of associating the output y to the
input x may or may not be a function.
domian rangex y=f(x)
f

6. A function f(x) = y takes an input x and produces
one output y. Often we represent a function by the
following figure.
Inverse Functions
We like to reverse the operation, i.e., if we know
the output y, what was (were) the input x?
This procedure of associating the output y to the
input x may or may not be a function.
domian rangex y=f(x)
f
If it is a function, it is called
the inverse function of f(x)
and it is denoted as f -1(y).

7. A function f(x) = y takes an input x and produces
one output y. Often we represent a function by the
following figure.
Inverse Functions
We like to reverse the operation, i.e., if we know
the output y, what was (were) the input x?
This procedure of associating the output y to the
input x may or may not be a function.
domian rangex y=f(x)
f
If it is a function, it is called
the inverse function of f(x)
and it is denoted as f -1(y).
x y=f(x)
f

8. A function f(x) = y takes an input x and produces
one output y. Often we represent a function by the
following figure.
Inverse Functions
We like to reverse the operation, i.e., if we know
the output y, what was (were) the input x?
This procedure of associating the output y to the
input x may or may not be a function.
domian rangex y=f(x)
f
If it is a function, it is called
the inverse function of f(x)
and it is denoted as f -1(y).
x=f-1(y) y=f(x)
f
f -1

9. A function f(x) = y takes an input x and produces
one output y. Often we represent a function by the
following figure.
Inverse Functions
We like to reverse the operation, i.e., if we know
the output y, what was (were) the input x?
This procedure of associating the output y to the
input x may or may not be a function.
domian rangex y=f(x)
f
If it is a function, it is called
the inverse function of f(x)
and it is denoted as f -1(y).
We say f(x) and f -1(y) are
the inverse of each other.
x=f-1(y) y=f(x)
f
f -1

10. Example A.
a. The function y = f(x) = 2x takes the input x and
doubles it to get the output y.
Inverse Functions

11. Example A.
a. The function y = f(x) = 2x takes the input x and
doubles it to get the output y. To reverse the
operation, take an output y,
Inverse Functions

12. Example A.
a. The function y = f(x) = 2x takes the input x and
doubles it to get the output y. To reverse the
operation, take an output y, divided it by 2 and we
get back to the x.
Inverse Functions

13. Example A.
a. The function y = f(x) = 2x takes the input x and
doubles it to get the output y. To reverse the
operation, take an output y, divided it by 2 and we
get back to the x. In other words f -1(y) = y/2.
Inverse Functions

14. Example A.
a. The function y = f(x) = 2x takes the input x and
doubles it to get the output y. To reverse the
operation, take an output y, divided it by 2 and we
get back to the x. In other words f -1(y) = y/2.
So, for example, f -1(6) = 3 because f(3) = 6.
Inverse Functions

15. Example A.
a. The function y = f(x) = 2x takes the input x and
doubles it to get the output y. To reverse the
operation, take an output y, divided it by 2 and we
get back to the x. In other words f -1(y) = y/2.
So, for example, f -1(6) = 3 because f(3) = 6.
b. Given y = f(x) = x2 and y = 9,
Inverse Functions

16. Example A.
a. The function y = f(x) = 2x takes the input x and
doubles it to get the output y. To reverse the
operation, take an output y, divided it by 2 and we
get back to the x. In other words f -1(y) = y/2.
So, for example, f -1(6) = 3 because f(3) = 6.
b. Given y = f(x) = x2 and y = 9, there are two
numbers, namely x = 3 and x = -3, associated to 9.
Inverse Functions

17. Example A.
a. The function y = f(x) = 2x takes the input x and
doubles it to get the output y. To reverse the
operation, take an output y, divided it by 2 and we
get back to the x. In other words f -1(y) = y/2.
So, for example, f -1(6) = 3 because f(3) = 6.
b. Given y = f(x) = x2 and y = 9, there are two
numbers, namely x = 3 and x = -3, associated to 9.
Therefore, the reverse procedure is not a function.
Inverse Functions

18. Example A.
a. The function y = f(x) = 2x takes the input x and
doubles it to get the output y. To reverse the
operation, take an output y, divided it by 2 and we
get back to the x. In other words f -1(y) = y/2.
So, for example, f -1(6) = 3 because f(3) = 6.
b. Given y = f(x) = x2 and y = 9, there are two
numbers, namely x = 3 and x = -3, associated to 9.
Therefore, the reverse procedure is not a function.
x=3
y=9
f(x)=x2
x=-3
not a function
Inverse Functions

19. A function is one-to-one if different inputs produce
different outputs.
Inverse Functions

20. A function is one-to-one if different inputs produce
different outputs. That is, f(x) is said to be
one-to-one if for every two inputs u and v such that
u  v, then f(u)  f(v).
Inverse Functions

21. A function is one-to-one if different inputs produce
different outputs. That is, f(x) is said to be
one-to-one if for every two inputs u and v such that
u  v, then f(u)  f(v).
Inverse Functions
u
v
u = v
a one-to-one function

22. A function is one-to-one if different inputs produce
different outputs. That is, f(x) is said to be
one-to-one if for every two inputs u and v such that
u  v, then f(u)  f(v).
Inverse Functions
u f(u)
v f(v)
u = v f(u) = f(v)
a one-to-one function

23. A function is one-to-one if different inputs produce
different outputs. That is, f(x) is said to be
one-to-one if for every two inputs u and v such that
u  v, then f(u)  f(v).
Inverse Functions
u f(u)
v f(v)
u = v f(u) = f(v)
a one-to-one function
u
v
u = v
not a one-to-one function

24. A function is one-to-one if different inputs produce
different outputs. That is, f(x) is said to be
one-to-one if for every two inputs u and v such that
u  v, then f(u)  f(v).
Inverse Functions
u f(u)
v f(v)
u = v f(u) = f(v)
a one-to-one function
u
f(u)=f(v)
v
u = v
not a one-to-one function

25. A function is one-to-one if different inputs produce
different outputs. That is, f(x) is said to be
one-to-one if for every two inputs u and v such that
u  v, then f(u)  f(v).
Example B.
a. g(x) = 2x is one-to-one
Inverse Functions
u f(u)
v f(v)
u = v f(u) = f(v)
a one-to-one function
u
f(u)=f(v)
v
u = v
not a one-to-one function

26. A function is one-to-one if different inputs produce
different outputs. That is, f(x) is said to be
one-to-one if for every two inputs u and v such that
u  v, then f(u)  f(v).
Example B.
a. g(x) = 2x is one-to-one
because if u  v, then 2u  2v.
Inverse Functions
u f(u)
v f(v)
u = v f(u) = f(v)
a one-to-one function
u
f(u)=f(v)
v
u = v
not a one-to-one function

27. A function is one-to-one if different inputs produce
different outputs. That is, f(x) is said to be
one-to-one if for every two inputs u and v such that
u  v, then f(u)  f(v).
Example B.
a. g(x) = 2x is one-to-one
because if u  v, then 2u  2v.
b. f(x) = x2 is not one-to-one
because 3  -3, but f(3) = f(-3) = 9.
Inverse Functions
u f(u)
v f(v)
u = v f(u) = f(v)
a one-to-one function
u
f(u)=f(v)
v
u = v
not a one-to-one function

28. A function is one-to-one if different inputs produce
different outputs. That is, f(x) is said to be
one-to-one if for every two inputs u and v such that
u  v, then f(u)  f(v).
Example B.
a. g(x) = 2x is one-to-one
because if u  v, then 2u  2v.
b. f(x) = x2 is not one-to-one
because 3  -3, but f(3) = f(-3) = 9.
Inverse Functions
u f(u)
v f(v)
u = v f(u) = f(v)
a one-to-one function
u
f(u)=f(v)
v
u = v
not a one-to-one function
Note:
To justify a function is 1-1,
we have to show that for every
pair of u  v that f(u)  f(v).

29. A function is one-to-one if different inputs produce
different outputs. That is, f(x) is said to be
one-to-one if for every two inputs u and v such that
u  v, then f(u)  f(v).
Example B.
a. g(x) = 2x is one-to-one
because if u  v, then 2u  2v.
b. f(x) = x2 is not one-to-one
because 3  -3, but f(3) = f(-3) = 9.
Inverse Functions
u f(u)
v f(v)
u = v f(u) = f(v)
a one-to-one function
u
f(u)=f(v)
v
u = v
not a one-to-one function
Note:
To justify a function is 1-1,
we have to show that for every
pair of u  v that f(u)  f(v).
To justify a function is not 1-1,
all we need is to produce one
pair of u  v but f(u) = f(v).

30. Fact: If y = f(x) is one-to-one, then the reverse
procedure for f(x) is a function
Inverse Functions

31. Fact: If y = f(x) is one-to-one, then the reverse
procedure for f(x) is a function i.e. f -1(y) exists.
Inverse Functions
Given y = f(x), to find f -1(y), just solve the equation
y = f(x) for x in terms of y.

32. Fact: If y = f(x) is one-to-one, then the reverse
procedure for f(x) is a function i.e. f -1(y) exists.
Inverse Functions
Example C.
Find the inverse function of y = f(x) = x – 53
4
Given y = f(x), to find f -1(y), just solve the equation
y = f(x) for x in terms of y.

33. Fact: If y = f(x) is one-to-one, then the reverse
procedure for f(x) is a function i.e. f -1(y) exists.
Inverse Functions
Example C.
Find the inverse function of y = f(x) = x – 5
Given y = x – 5 and solve for x.
3
4
3
4
Given y = f(x), to find f -1(y), just solve the equation
y = f(x) for x in terms of y.

34. Fact: If y = f(x) is one-to-one, then the reverse
procedure for f(x) is a function i.e. f -1(y) exists.
Inverse Functions
Example C.
Find the inverse function of y = f(x) = x – 5
Given y = x – 5 and solve for x.
Clear denominator: 4y = 3x – 20
3
4
3
4
Given y = f(x), to find f -1(y), just solve the equation
y = f(x) for x in terms of y.

35. Fact: If y = f(x) is one-to-one, then the reverse
procedure for f(x) is a function i.e. f -1(y) exists.
Inverse Functions
Example C.
Find the inverse function of y = f(x) = x – 5
Given y = x – 5 and solve for x.
Clear denominator: 4y = 3x – 20
4y + 20 = 3x
3
4
3
4
Given y = f(x), to find f -1(y), just solve the equation
y = f(x) for x in terms of y.

36. Fact: If y = f(x) is one-to-one, then the reverse
procedure for f(x) is a function i.e. f -1(y) exists.
Inverse Functions
Example C.
Find the inverse function of y = f(x) = x – 5
Given y = x – 5 and solve for x.
Clear denominator: 4y = 3x – 20
4y + 20 = 3x
x =
3
4
3
4
4y + 20
3
Given y = f(x), to find f -1(y), just solve the equation
y = f(x) for x in terms of y.

37. Fact: If y = f(x) is one-to-one, then the reverse
procedure for f(x) is a function i.e. f -1(y) exists.
Inverse Functions
Example C.
Find the inverse function of y = f(x) = x – 5
Given y = x – 5 and solve for x.
Clear denominator: 4y = 3x – 20
4y + 20 = 3x
x =
3
4
3
4
4y + 20
3
Given y = f(x), to find f -1(y), just solve the equation
y = f(x) for x in terms of y.
Hence f -1(y) =
4y + 20
3

38. Inverse Functions
Reminder: If f(x) and f -1(y) are the inverse of each
other, then f(a) = b if and only if a = f -1(b)

39. Inverse Functions
Since we usually use x as the input variable for
functions, we often use x instead of y as the variable
for the inverse functions.
Reminder: If f(x) and f -1(y) are the inverse of each
other, then f(a) = b if and only if a = f -1(b)

40. Inverse Functions
Since we usually use x as the input variable for
functions, we often use x instead of y as the variable
for the inverse functions. Hence in example C, the
answer may be written as f -1(x) = 4x + 20
3 .
Reminder: If f(x) and f -1(y) are the inverse of each
other, then f(a) = b if and only if a = f -1(b)

41. Fact: If f(x) and f -1(y) are the inverse of each other,
then f -1(f(x)) = x
Inverse Functions
Since we usually use x as the input variable for
functions, we often use x instead of y as the variable
for the inverse functions. Hence in example C, the
answer may be written as f -1(x) = 4x + 20
3 .
Reminder: If f(x) and f -1(y) are the inverse of each
other, then f(a) = b if and only if a = f -1(b)

42. Fact: If f(x) and f -1(y) are the inverse of each other,
then f -1(f(x)) = x
Inverse Functions
Since we usually use x as the input variable for
functions, we often use x instead of y as the variable
for the inverse functions. Hence in example C, the
answer may be written as f -1(x) = 4x + 20
3 .
Reminder: If f(x) and f -1(y) are the inverse of each
other, then f(a) = b if and only if a = f -1(b)
Using f(x) as input,
plug it into f -1.

43. Fact: If f(x) and f -1(y) are the inverse of each other,
then f -1(f(x)) = x
Inverse Functions
Since we usually use x as the input variable for
functions, we often use x instead of y as the variable
for the inverse functions. Hence in example C, the
answer may be written as f -1(x) = 4x + 20
3 .
Reminder: If f(x) and f -1(y) are the inverse of each
other, then f(a) = b if and only if a = f -1(b)
x f(x)
f
Using f(x) as input,
plug it into f -1.

44. Fact: If f(x) and f -1(y) are the inverse of each other,
then f -1(f(x)) = x
Inverse Functions
Since we usually use x as the input variable for
functions, we often use x instead of y as the variable
for the inverse functions. Hence in example C, the
answer may be written as f -1(x) = 4x + 20
3 .
Reminder: If f(x) and f -1(y) are the inverse of each
other, then f(a) = b if and only if a = f -1(b)
x f(x)
f
f -1
f -1(f(x)) = x
Using f(x) as input,
plug it into f -1.

45. Fact: If f(x) and f -1(y) are the inverse of each other,
then f -1(f(x)) = x and f(f -1(x)) = x.
Inverse Functions
Since we usually use x as the input variable for
functions, we often use x instead of y as the variable
for the inverse functions. Hence in example C, the
answer may be written as f -1(x) = 4x + 20
3 .
Reminder: If f(x) and f -1(y) are the inverse of each
other, then f(a) = b if and only if a = f -1(b)
x f(x)
f
f -1
f -1(f(x)) = x
Using f(x) as input,
plug it into f -1.
Using f -1(x) as input,
plug it into f.

46. Fact: If f(x) and f -1(y) are the inverse of each other,
then f -1(f(x)) = x and f(f -1(x)) = x.
Inverse Functions
Since we usually use x as the input variable for
functions, we often use x instead of y as the variable
for the inverse functions. Hence in example C, the
answer may be written as f -1(x) = 4x + 20
3 .
Reminder: If f(x) and f -1(y) are the inverse of each
other, then f(a) = b if and only if a = f -1(b)
f-1(x) x
f -1
x f(x)
f
f -1
f -1(f(x)) = x
Using f(x) as input,
plug it into f -1.
Using f -1(x) as input,
plug it into f.

47. Fact: If f(x) and f -1(y) are the inverse of each other,
then f -1(f(x)) = x and f(f -1(x)) = x.
Inverse Functions
Since we usually use x as the input variable for
functions, we often use x instead of y as the variable
for the inverse functions. Hence in example C, the
answer may be written as f -1(x) = 4x + 20
3 .
Reminder: If f(x) and f -1(y) are the inverse of each
other, then f(a) = b if and only if a = f -1(b)
f-1(x) x
f
f -1
x f(x)
f
f -1
f -1(f(x)) = x f(f -1(x)) = x
Using f(x) as input,
plug it into f -1.
Using f -1(x) as input,
plug it into f.

48. Example D.
2x – 3
x + 2
Inverse Functions
a. Given f(x) = find f -1(x).,

49. Example D.
2x – 3
x + 2
Inverse Functions
a. Given f(x) = find f -1(x).,
Set y = and solve for x in term of y.
2x – 3
x + 2 ,

50. Example D.
2x – 3
x + 2
Inverse Functions
a. Given f(x) = find f -1(x).,
Set y = and solve for x in term of y.
2x – 3
x + 2 ,
Clear the denominator, we get
y(x + 2) = 2x – 3

51. Example D.
2x – 3
x + 2
Inverse Functions
a. Given f(x) = find f -1(x).,
Set y = and solve for x in term of y.
2x – 3
x + 2 ,
Clear the denominator, we get
y(x + 2) = 2x – 3
yx + 2y = 2x – 3 collecting and
isolating x

52. Example D.
2x – 3
x + 2
Inverse Functions
a. Given f(x) = find f -1(x).,
Set y = and solve for x in term of y.
2x – 3
x + 2 ,
Clear the denominator, we get
y(x + 2) = 2x – 3
yx + 2y = 2x – 3 collecting and
isolating xyx – 2x = –2y – 3

53. Example D.
2x – 3
x + 2
Inverse Functions
a. Given f(x) = find f -1(x).,
Set y = and solve for x in term of y.
2x – 3
x + 2 ,
Clear the denominator, we get
y(x + 2) = 2x – 3
yx + 2y = 2x – 3 collecting and
isolating xyx – 2x = –2y – 3
(y – 2)x = –2y – 3

54. Example D.
Hence f -1(y) =
2x – 3
x + 2
Inverse Functions
a. Given f(x) = find f -1(x).,
Set y = and solve for x in term of y.
2x – 3
x + 2 ,
Clear the denominator, we get
y(x + 2) = 2x – 3
yx + 2y = 2x – 3 collecting and
isolating xyx – 2x = –2y – 3
(y – 2)x = –2y – 3
x =
–2y – 3
y – 2
–2y – 3
y – 2

55. Example D.
Hence f -1(y) =
2x – 3
x + 2
Inverse Functions
a. Given f(x) = find f -1(x).,
Set y = and solve for x in term of y.
2x – 3
x + 2 ,
Clear the denominator, we get
y(x + 2) = 2x – 3
yx + 2y = 2x – 3 collecting and
isolating xyx – 2x = –2y – 3
(y – 2)x = –2y – 3
x =
–2y – 3
y – 2
–2y – 3
y – 2
Write the answer using x as the variable:
f -1(x) =
–2x – 3
x – 2

56. Inverse Functions
b. Verify that f(f -1(x)) = x

57. Inverse Functions
b. Verify that f(f -1(x)) = x
We've f(x) = and
2x – 3
x + 2 , f -1(x) =
–2x – 3
x – 2

58. Inverse Functions
b. Verify that f(f -1(x)) = x
We've f(x) = and
2x – 3
x + 2 , f -1(x) =
–2x – 3
x – 2
f(f -1(x)) = f( )–2x – 3
x – 2

59. Inverse Functions
b. Verify that f(f -1(x)) = x
We've f(x) = and
2x – 3
x + 2 , f -1(x) =
–2x – 3
x – 2
f(f -1(x)) = f( )–2x – 3
x – 2
=
–2x – 3
x – 2
– 3
–2x – 3
x – 2
+ 2
( )2

60. Inverse Functions
b. Verify that f(f -1(x)) = x
We've f(x) = and
2x – 3
x + 2 , f -1(x) =
–2x – 3
x – 2
f(f -1(x)) = f( )–2x – 3
x – 2
=
–2x – 3
x – 2
– 3
–2x – 3
x – 2
+ 2
( )2
Use the LCD to simplify
the complex fraction

61. Inverse Functions
b. Verify that f(f -1(x)) = x
We've f(x) = and
2x – 3
x + 2 , f -1(x) =
–2x – 3
x – 2
f(f -1(x)) = f( )–2x – 3
x – 2
=
–2x – 3
x – 2
– 3
–2x – 3
x – 2
+ 2
( )2[
[ ]
](x – 2)
(x – 2)
Use the LCD to simplify
the complex fraction

62. Inverse Functions
b. Verify that f(f -1(x)) = x
We've f(x) = and
2x – 3
x + 2 , f -1(x) =
–2x – 3
x – 2
f(f -1(x)) = f( )–2x – 3
x – 2
=
–2x – 3
x – 2
– 3
–2x – 3
x – 2
+ 2
( )2[
[ ]
](x – 2)
(x – 2)
=
2(-2x – 3) – 3(x – 2)
(-2x – 3) + 2(x – 2)
Use the LCD to simplify
the complex fraction

63. Inverse Functions
b. Verify that f(f -1(x)) = x
We've f(x) = and
2x – 3
x + 2 , f -1(x) =
–2x – 3
x – 2
f(f -1(x)) = f( )–2x – 3
x – 2
=
–2x – 3
x – 2
– 3
–2x – 3
x – 2
+ 2
( )2[
[ ]
](x – 2)
(x – 2)
=
2(-2x – 3) – 3(x – 2)
(-2x – 3) + 2(x – 2)
=
-4x – 6 – 3x + 6
-2x – 3 + 2x – 4
Use the LCD to simplify
the complex fraction

64. Inverse Functions
b. Verify that f(f -1(x)) = x
We've f(x) = and
2x – 3
x + 2 , f -1(x) =
–2x – 3
x – 2
f(f -1(x)) = f( )–2x – 3
x – 2
=
–2x – 3
x – 2
– 3
–2x – 3
x – 2
+ 2
( )2[
[ ]
](x – 2)
(x – 2)
=
2(-2x – 3) – 3(x – 2)
(-2x – 3) + 2(x – 2)
=
-4x – 6 – 3x + 6
-2x – 3 + 2x – 4
=
-7x
-7
= x
Your turn. Verify that f -1(f(x)) = x
Use the LCD to simplify
the complex fraction

65. There is no inverse for x2 with the set of all real
numbers R as the domain because x2 is not a 1–1
function over R.
Graphs of Inverse Functions

66. There is no inverse for x2 with the set of all real
numbers R as the domain because x2 is not a 1–1
function over R. However, if we set the domain to be
A = {x ≥ 0} (non–negative numbers) then the function
g(x) = x2 is a 1–1 function with the range B = {y ≥ 0}.
Graphs of Inverse Functions

67. There is no inverse for x2 with the set of all real
numbers R as the domain because x2 is not a 1–1
function over R. However, if we set the domain to be
A = {x ≥ 0} (non–negative numbers) then the function
g(x) = x2 is a 1–1 function with the range B = {y ≥ 0}.
Graphs of Inverse Functions
Hence g–1 exists.

68. There is no inverse for x2 with the set of all real
numbers R as the domain because x2 is not a 1–1
function over R. However, if we set the domain to be
A = {x ≥ 0} (non–negative numbers) then the function
g(x) = x2 is a 1–1 function with the range B = {y ≥ 0}.
Graphs of Inverse Functions
Hence g–1 exists. To find it,
set y = g(x) = x2,

69. There is no inverse for x2 with the set of all real
numbers R as the domain because x2 is not a 1–1
function over R. However, if we set the domain to be
A = {x ≥ 0} (non–negative numbers) then the function
g(x) = x2 is a 1–1 function with the range B = {y ≥ 0}.
Graphs of Inverse Functions
Hence g–1 exists. To find it,
set y = g(x) = x2, solve for x
we’ve x = ±√y.

70. There is no inverse for x2 with the set of all real
numbers R as the domain because x2 is not a 1–1
function over R. However, if we set the domain to be
A = {x ≥ 0} (non–negative numbers) then the function
g(x) = x2 is a 1–1 function with the range B = {y ≥ 0}.
Graphs of Inverse Functions
Hence g–1 exists. To find it,
set y = g(x) = x2, solve for x
we’ve x = ±√y.
Since x is non–negative we
must have
x = √y = g–1(y)

71. There is no inverse for x2 with the set of all real
numbers R as the domain because x2 is not a 1–1
function over R. However, if we set the domain to be
A = {x ≥ 0} (non–negative numbers) then the function
g(x) = x2 is a 1–1 function with the range B = {y ≥ 0}.
Graphs of Inverse Functions
Hence g–1 exists. To find it,
set y = g(x) = x2, solve for x
we’ve x = ±√y.
Since x is non–negative we
must have
x = √y = g–1(y) or that
g–1(x) = √x.

72. There is no inverse for x2 with the set of all real
numbers R as the domain because x2 is not a 1–1
function over R. However, if we set the domain to be
A = {x ≥ 0} (non–negative numbers) then the function
g(x) = x2 is a 1–1 function with the range B = {y ≥ 0}.
Graphs of Inverse Functions
Hence g–1 exists. To find it,
set y = g(x) = x2, solve for x
we’ve x = ±√y.
Since x is non–negative we
must have
x = √y = g–1(y) or that
g–1(x) = √x.
g(x) = x2
g–1(x) = √x
Here are their graphs.
y = x

73. There is no inverse for x2 with the set of all real
numbers R as the domain because x2 is not a 1–1
function over R. However, if we set the domain to be
A = {x ≥ 0} (non–negative numbers) then the function
g(x) = x2 is a 1–1 function with the range B = {y ≥ 0}.
Graphs of Inverse Functions
Hence g–1 exists. To find it,
set y = g(x) = x2, solve for x
we’ve x = ±√y.
Since x is non–negative we
must have
x = √y = g–1(y) or that
g–1(x) = √x.
g(x) = x2
Here are their graphs.
We note the symmetry of their graphs below.
y = x
g–1(x) = √x

74. Graphs of Inverse Functions
y
Let f and f –1 be a pair of
inverse functions where
f(a) = b so that f –1(b) = a.
The graph of y = f –1(x)
x
y = f(x)

75. Graphs of Inverse Functions
(a, b)
y = f(x)y
Let f and f –1 be a pair of
inverse functions where
f(a) = b so that f –1(b) = a.
Hence the point (a, b) is
on the graph of y = f(x)
and the point (b, a) is on
the graph of y = f –1(x).
The graph of y = f –1(x)
x

76. Graphs of Inverse Functions
(a, b)
(b, a)
y = f(x)y
Let f and f –1 be a pair of
inverse functions where
f(a) = b so that f –1(b) = a.
Hence the point (a, b) is
on the graph of y = f(x)
and the point (b, a) is on
the graph of y = f –1(x).
Graphically (a, b) & (b, a)
are mirror images with
respect to the line y = x.
y=x
The graph of y = f –1(x)
x

77. Graphs of Inverse Functions
(a, b)
(b, a)
y = f(x)
(x, y)
(y, x)
y
Let f and f –1 be a pair of
inverse functions where
f(a) = b so that f –1(b) = a.
Hence the point (a, b) is
on the graph of y = f(x)
and the point (b, a) is on
the graph of y = f –1(x).
Graphically (a, b) & (b, a)
are mirror images with
respect to the line y = x.
y=x
The graph of y = f –1(x)
x

78. Graphs of Inverse Functions
y = f–1 (x)
(a, b)
(b, a)
y = f(x)
(x, y)
(y, x)
y
Let f and f –1 be a pair of
inverse functions where
f(a) = b so that f –1(b) = a.
Hence the point (a, b) is
on the graph of y = f(x)
and the point (b, a) is on
the graph of y = f –1(x).
Graphically (a, b) & (b, a)
are mirror images with
respect to the line y = x.
y=x
So the graph of y = f –1(x) is the diagonal reflection of
the graph of y = f(x).
The graph of y = f –1(x)
x

79. Graphs of Inverse Functions
y = f–1 (x)
(a, b)
(b, a)
y = f(x)
(x, y)
(y, x)
y
(c, c), a fixed point
Let f and f –1 be a pair of
inverse functions where
f(a) = b so that f –1(b) = a.
Hence the point (a, b) is
on the graph of y = f(x)
and the point (b, a) is on
the graph of y = f –1(x).
Graphically (a, b) & (b, a)
are mirror images with
respect to the line y = x.
y=x
So the graph of y = f –1(x) is the diagonal reflection of
the graph of y = f(x).
The graph of y = f –1(x)
x

80. Graphs of Inverse Functions
y = f–1 (x)
(a, b)
(b, a)
y = f(x)
(x, y)
(y, x)
x
y
(c, c), a fixed point
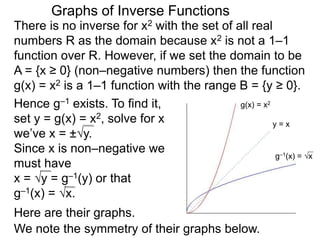
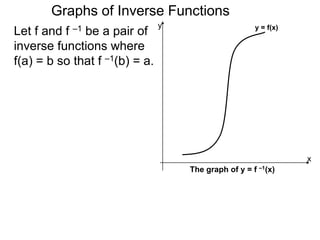
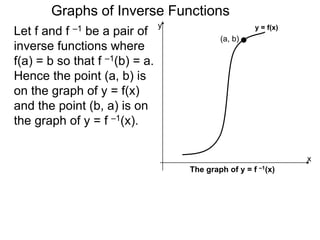
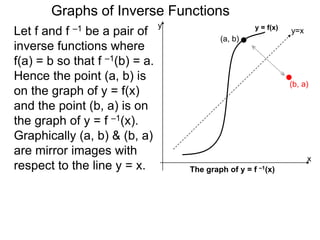
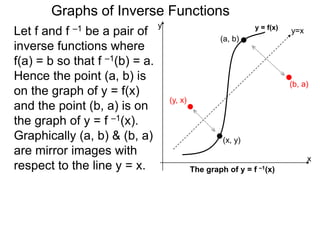
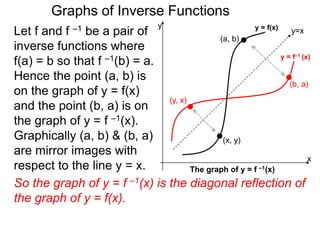
Let f and f –1 be a pair of
inverse functions where
f(a) = b so that f –1(b) = a.
Hence the point (a, b) is
on the graph of y = f(x)
and the point (b, a) is on
the graph of y = f –1(x).
Graphically (a, b) & (b, a)
are mirror images with
respect to the line y = x.
y=x
So the graph of y = f –1(x) is the diagonal reflection of
the graph of y = f(x). If the domain of f(x) is [A, B]
The graph of y = f –1(x)
A B

81. Graphs of Inverse Functions
y = f–1 (x)
(a, b)
(b, a)
y = f(x)
(x, y)
(y, x)
x
y
(c, c), a fixed point
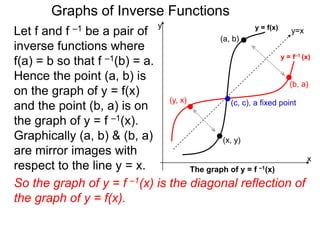
Let f and f –1 be a pair of
inverse functions where
f(a) = b so that f –1(b) = a.
Hence the point (a, b) is
on the graph of y = f(x)
and the point (b, a) is on
the graph of y = f –1(x).
Graphically (a, b) & (b, a)
are mirror images with
respect to the line y = x.
y=x
So the graph of y = f –1(x) is the diagonal reflection of
the graph of y = f(x). If the domain of f(x) is [A, B] and
its range is [C, D],
The graph of y = f –1(x)
A B
C
D

82. Graphs of Inverse Functions
y = f–1 (x)
(a, b)
(b, a)
y = f(x)
(x, y)
(y, x)
x
y
(c, c), a fixed point
Let f and f –1 be a pair of
inverse functions where
f(a) = b so that f –1(b) = a.
Hence the point (a, b) is
on the graph of y = f(x)
and the point (b, a) is on
the graph of y = f –1(x).
Graphically (a, b) & (b, a)
are mirror images with
respect to the line y = x.
y=x
So the graph of y = f –1(x) is the diagonal reflection of
the graph of y = f(x). If the domain of f(x) is [A, B] and
its range is [C, D], then the domain of f –1(x) is [C, D],
The graph of y = f –1(x)
A B
C
D
DC

83. Graphs of Inverse Functions
y = f–1 (x)
(a, b)
(b, a)
y = f(x)
(x, y)
(y, x)
x
y
(c, c), a fixed point
Let f and f –1 be a pair of
inverse functions where
f(a) = b so that f –1(b) = a.
Hence the point (a, b) is
on the graph of y = f(x)
and the point (b, a) is on
the graph of y = f –1(x).
Graphically (a, b) & (b, a)
are mirror images with
respect to the line y = x.
y=x
So the graph of y = f –1(x) is the diagonal reflection of
the graph of y = f(x). If the domain of f(x) is [A, B] and
its range is [C, D], then the domain of f –1(x) is [C, D],
with [A, B] as its range.
The graph of y = f –1(x)
A B
C
D
B
A
DC

84. Graphs of Inverse Functions
(–1, 3)
y = f(x)Example E. Given the graph of
y = f(x) as shown, draw the
graph of y = f –1(x). Label the
domain and range of y = f –1(x)
clearly.
x
y
(1, 1)
(2, –3)

85. Graphs of Inverse Functions
(–1, 3)
y = f(x)Example E. Given the graph of
y = f(x) as shown, draw the
graph of y = f –1(x). Label the
domain and range of y = f –1(x)
clearly.
x
y
(1, 1)
(2, –3)
The graph of y = f –1(x) is the
diagonal reflection of y = f(x).

86. Graphs of Inverse Functions
(–1, 3)
y = f(x)Example E. Given the graph of
y = f(x) as shown, draw the
graph of y = f –1(x). Label the
domain and range of y = f –1(x)
clearly.
x
y
(1, 1)
(2, –3)
The graph of y = f –1(x) is the
diagonal reflection of y = f(x).
Tracking the reflections of the
end points:
(–1, 3)
y = f(x)
x
(2, –3)

87. Graphs of Inverse Functions
(–1, 3)
y = f(x)Example E. Given the graph of
y = f(x) as shown, draw the
graph of y = f –1(x). Label the
domain and range of y = f –1(x)
clearly.
x
y
(1, 1)
(2, –3)
The graph of y = f –1(x) is the
diagonal reflection of y = f(x).
Tracking the reflections of the
end points:
(–1, 3)→(3, –1),
(–1, 3)
y = f(x)
x
(2, –3)
(3, –1)

88. Graphs of Inverse Functions
(–1, 3)
y = f(x)Example E. Given the graph of
y = f(x) as shown, draw the
graph of y = f –1(x). Label the
domain and range of y = f –1(x)
clearly.
x
y
(1, 1)
(2, –3)
The graph of y = f –1(x) is the
diagonal reflection of y = f(x).
Tracking the reflections of the
end points:
(–1, 3)→(3, –1), (2, –3)→(–3, 2)
(–1, 3)
y = f(x)
x
(2, –3)
(–3, 2)
(3, –1)

89. Graphs of Inverse Functions
(–1, 3)
y = f(x)Example E. Given the graph of
y = f(x) as shown, draw the
graph of y = f –1(x). Label the
domain and range of y = f –1(x)
clearly.
x
y
(1, 1)
(2, –3)
The graph of y = f –1(x) is the
diagonal reflection of y = f(x).
Tracking the reflections of the
end points:
(–1, 3)→(3, –1), (2, –3)→(–3, 2)
and (1, 1) is fixed.
(–1, 3)
y = f(x)
x
(1, 1)
(2, –3)
(–3, 2)
(3, –1)
y = f–1(x)

90. Graphs of Inverse Functions
(–1, 3)
y = f(x)Example E. Given the graph of
y = f(x) as shown, draw the
graph of y = f –1(x). Label the
domain and range of y = f –1(x)
clearly.
x
y
(1, 1)
(2, –3)
The graph of y = f –1(x) is the
diagonal reflection of y = f(x).
Tracking the reflections of the
end points:
(–1, 3)→(3, –1), (2, –3)→(–3, 2)
and (1, 1) is fixed.
Using these reflected points, draw the
reflection for the graph of y = f –1(x).
(–1, 3)
y = f(x)
x
(1, 1)
(2, –3)
(–3, 2)
(3, –1)
y = f–1(x)

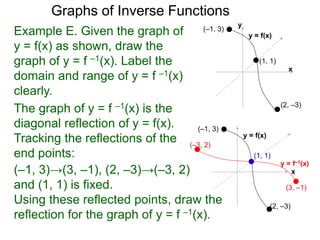
91. Graphs of Inverse Functions
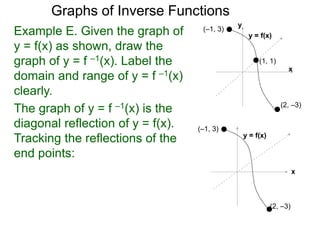
(–1, 3)
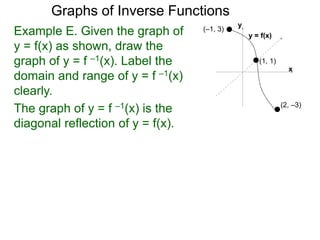
y = f(x)Example E. Given the graph of
y = f(x) as shown, draw the
graph of y = f –1(x). Label the
domain and range of y = f –1(x)
clearly.
x
y
(1, 1)
(2, –3)
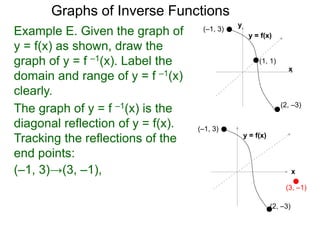
The graph of y = f –1(x) is the
diagonal reflection of y = f(x).
Tracking the reflections of the
end points:
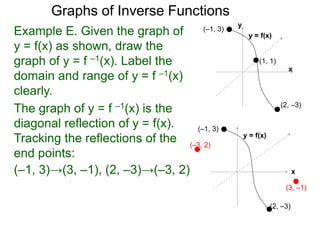
(–1, 3)→(3, –1), (2, –3)→(–3, 2)
and (1, 1) is fixed.
Using these reflected points, draw the
reflection for the graph of y = f –1(x).
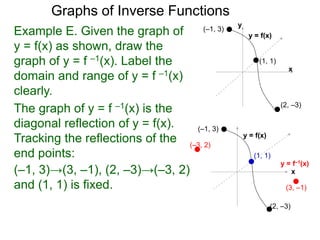
(–1, 3)
y = f(x)
x
(1, 1)
(2, –3)
(–3, 2)
(3, –1)
y = f–1(x)
The domain of f –1(x) is [–3, 3] with [–1, 2] as its range.

92. Exercise A.
Hence f -1(y) =
2x – 3
x + 2
Inverse Functions
a. Given f(x) = find f -1(x).,
Set y = and solve for x in term of y.
2x – 3
x + 2 ,
Clear the denominator, we get y(x + 2) = 2x – 3
yx + 2y = 2x – 3 collecting and
isolating xyx – 2x = –2y – 3
(y – 2)x = –2y – 3
x =
–2y – 3
y – 2
–2y – 3
y – 2
Write the answer using x as the variable:
f -1(x) =
–2x – 3
x – 2

93. Exercise A. Find the inverse f -1(x) of the following f(x)’s.
Inverse Functions
2. f(x) = x/3 – 2
2x – 3
x + 2
1. f(x) = 3x – 2 3. f(x) = x/3 + 2/5
5. f(x) = 3/x – 24. f(x) = ax + b 6. f(x) = 4/x + 2/5
7. f(x) = 3/(x – 2) 8. f(x) = 4/(x + 2) – 5
9. f(x) = 2/(3x + 4) – 5 10. f(x) = 5/(4x + 3) – 1/2
f(x) =11. 2x – 3
x + 2f(x) =12.
4x – 3
–3x + 2
f(x) =13.
bx + c
a
f(x) =14. cx + d
ax + b
f(x) =15.
16. f(x) = (3x – 2)1/3
18. f(x) = (x/3 – 2)1/3
17. f(x) = (x/3 + 2/5)1/3
19. f(x) = (x/3)1/3 – 2
20. f(x) = (ax – b)1/3 21. f(x) = (ax)1/3 – b
B. Verify your answers are correct by verifying that
f -1(f(x)) = x and f(f-1 (x)) = x for problem 1 – 21.

94. C. For each of the following graphs of f(x)’s, determine
a. the domain and the range of the f -1(x),
b. the end points and the fixed points of the graph of f -1(x).
Draw the graph of f -1(x).
Inverse Functions
(–3, –1)
y = x
(3,4)
1.
(–4, –2)
(5,7)
2.
(–2, –5)
(4,3)
3.
(–3, –1)
(3,4)4.
(–4, –2)
(5,7)
5.
(–2, –5)
(4,3)
6.

95. Inverse Functions
(2, –1)
7.
(–4, 3)
(c, d)
8.
(a, b)
C. For each of the following graphs of f(x)’s, determine
a. the domain and the range of the f -1(x),
b. the end points and the fixed points of the graph of f -1(x).
Draw the graph of f -1(x).

96. (Answers to the odd problems) Exercise A.
Inverse Functions
2x + 3
2 – x
1. f -1(x) = (x + 2) 3. f -1(x) = (5x – 2)
5. f -1(x) = 7. f -1(x) =
9. f -1(x) = – f -1(x) =11.
2x + 3
3x + 4
f -1 (x) =13. x – ac
ad – b
f -1 (x) =15.
17. f -1(x) = (5x3 – 2) 19. f -1(x) = 3 (x3 + 6x2 + 12x + 8)
21. f(x) = a3 + 3a2b + 3ab2 + b3
1
3
3
5
3
x + 2
2x + 3
x
2(2x + 9)
3(x + 5)
3
5
x

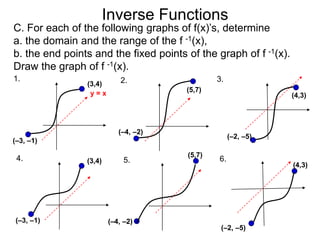
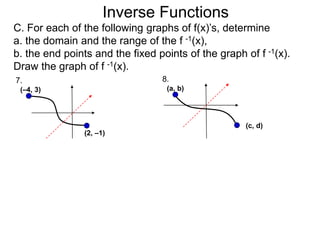
97. Exercise C.
Inverse Functions
(4, 3)
y = x
(-1, -3)
1. domain: [-1, 4]
range: [-3, 3]
(–5, –2)
(3,4)
3. domain: [-5, 3]
range: [-2, 4]
(–2, –4)
(7,5)
5. domain: [-2, 7]
range: [-4, 5]
(3, –4)
7. domain: [-1, 3], range: [-4,2]
(–1, 2)