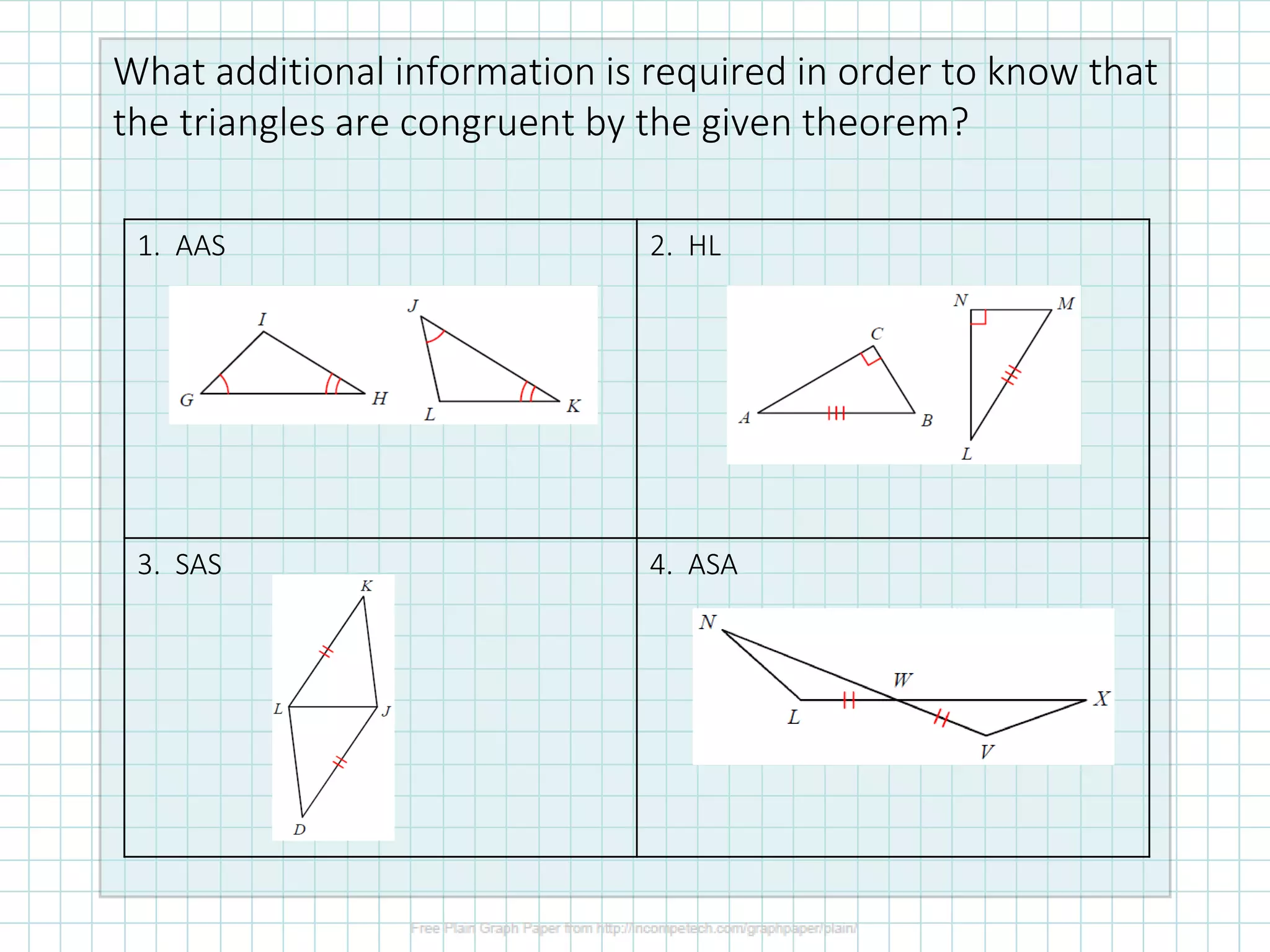
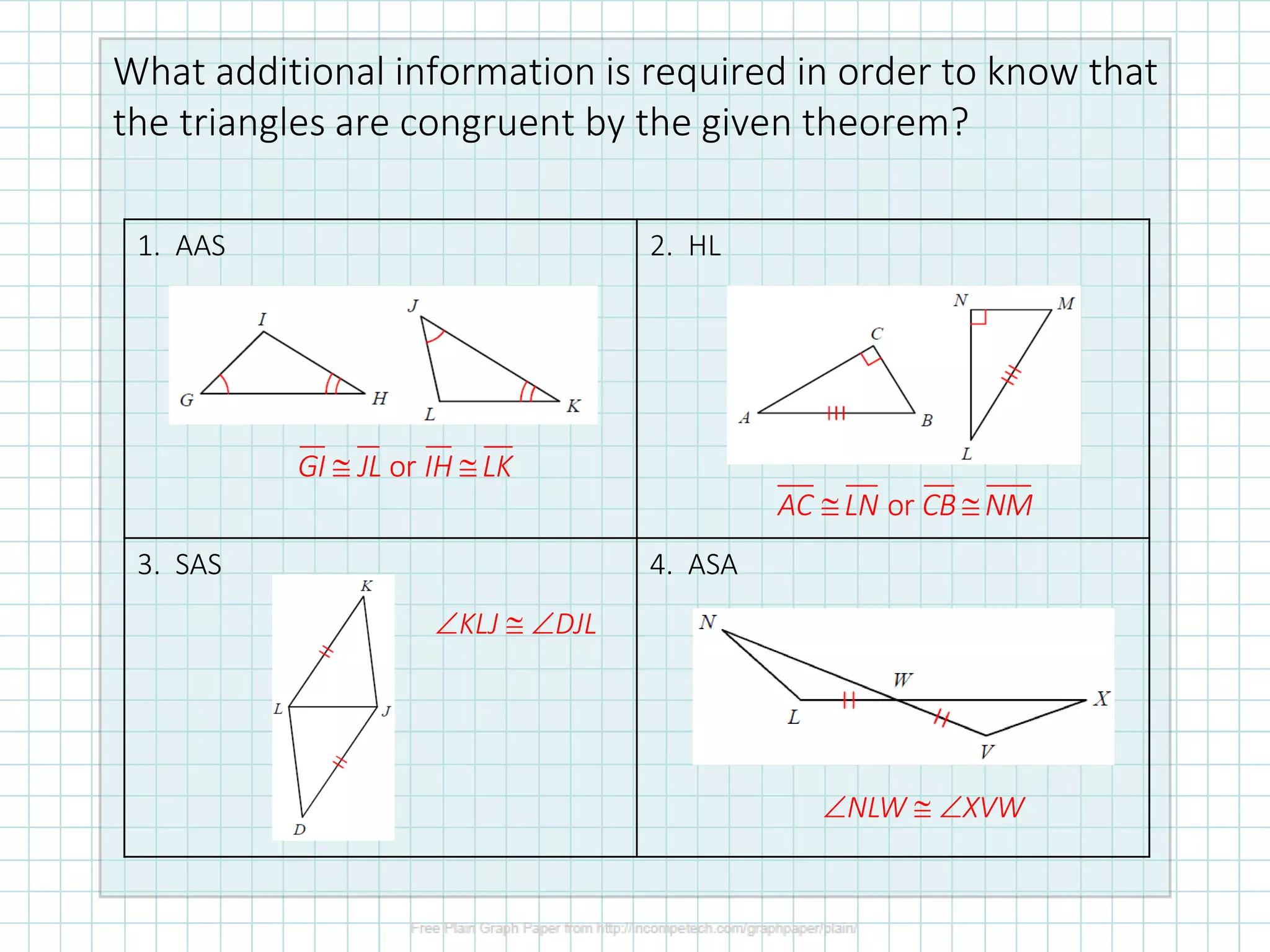
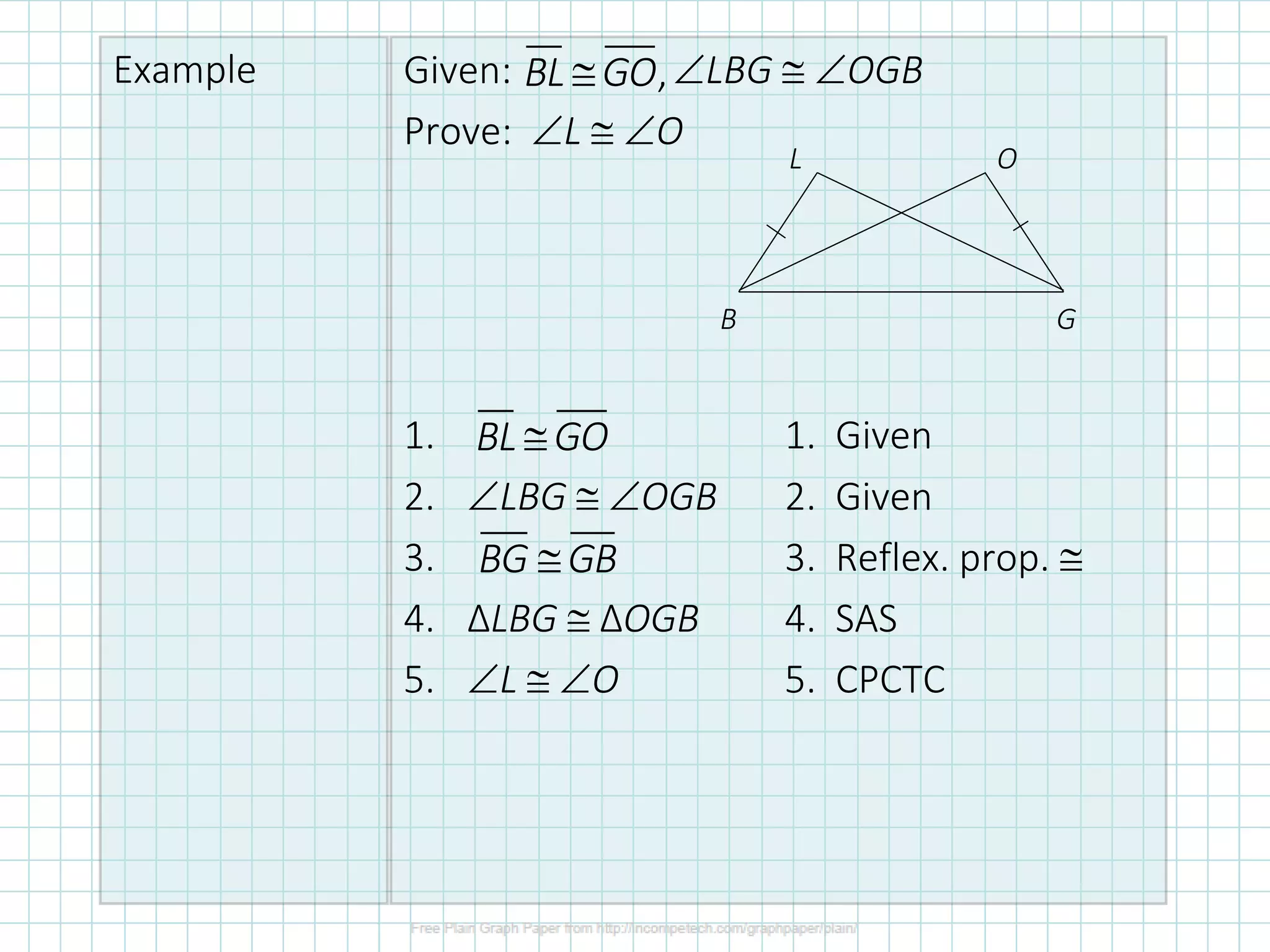
1. The document discusses different methods for proving triangles congruent, including using congruence theorems like SAS, SSS, ASA, and CPCTC (corresponding parts of congruent triangles are congruent). 2. It provides an example proof demonstrating the three step process: 1) mark given information, 2) identify the congruence theorem, 3) write statements and reasons. 3. Common reasons used in proofs include the reflexive property of congruence, vertical angles theorem, and parallel line theorems like corresponding angles.

1. Congruent Triangle Proofs & CPCTC
The student is able to (I can):
• Determine what additional information is needed to prove
two triangles congruent by a given theorem
• Create two-column proofs to show that two triangles are
congruent
• Show that corresponding parts of congruent triangles are
congruent.

2. What additional information is required in order to know that
the triangles are congruent by the given theorem?
1. AAS 2. HL
3. SAS 4. ASA

3. What additional information is required in order to know that
the triangles are congruent by the given theorem?
1. AAS 2. HL
3. SAS 4. ASA
orGI JL IH LK 
orAC LN CB NM 
KLJ  DJL
NLW  XVW

4. When you are creating a proof, you list the information that
you are given, list any other information you can deduce, and
then whatever it is you are trying to prove.
It is equally important that you give reasons for each step
that you list, whether you are listing given information or
information you have deduced using theorems and
postulates.
While congruent triangle proofs can be a little challenging, I
have a basic three-step method that I use to set them up.

5. Three Steps to a Proof
Step 1: Mark the given information on the diagram and any
other information you know such as vertical angles,
a shared side, or angles formed by parallel lines.
Step 2: Identify the congruence theorem to be used and the
additional information needed and why.
Step 3: Write down the statements and the reasons. Make
sure your last statement is what you are supposed
to be proving.

6. Example Given:
Prove: ΔABD  ΔCBD
Step 1: Based on the given information, mark the congruent
sides with matching pairs of tick marks.
 andAB BC AD CD
A
B
C
D

7. Example Given:
Prove: ΔABD  ΔCBD
Step 1: Based on the given information, mark the congruent
sides with matching pairs of tick marks.
Step 2: We have two sides congruent, so we will either use
SSS or SAS. (Remember, SSA is not valid!) We have
a shared side (and no angle indications), so we will
use SSS.
andAB BC AD CD 
A
B
C
D

8. Example Given:
Prove: ΔABD  ΔCBD
Step 1: Based on the given information, mark the congruent
sides with matching pairs of tick marks.
Step 2: We have two sides congruent, so we will either use
SSS or SAS. (Remember, SSA is not valid!) We have
a shared side (and no angle indications), so we will
use SSS.
Step 3: Write the proof, with one statement and reason for
each side, and the final statement is what we are
proving.
andAB BC AD CD 
A
B
C
D

9. Example Given:
Prove: ΔABD  ΔCBD
Step 3:
andAB BC AD CD 
A
B
C
D
Statements Reasons
S 1. 1. Given
S 2. 2. Given
S 3. 3. Refl. prop. 
4. ΔABD  ΔCBD 4. SSS
AB BC
AD CD
BD BD

10. Remember, any definition, theorem, or postulate we have
worked with this year is fair game on a proof, but here are
the most common ones we will use:
• Reflexive property of congruence (Refl. prop. )
(Use on shared sides or shared angles)
• Vertical angles theorem (Vert. s )
• Midpoint theorem (Midpt. thm)
• Segment and/or angle bisectors
• Any of the parallel line theorems
– Corresponding angles (Corr. s )
– Alternate interior angles (Alt. int. s )
– Alternate exterior angles (Alt.ext. s )

11. CPCTC – an abbreviation for “Corresponding Parts of
Congruent Triangles are Congruent.”
Once we know two triangles are congruent, we then know
that all of their corresponding sides and angles are
congruent.
To use CPCTC, first prove the triangles congruent using SSS,
SAS, ASA, AAS, or HL, and then use CPCTC to state that the
other parts of the triangle are also congruent.

12. Example Given: LBG  OGB
Prove: L  O
1. 1. Given
2. LBG  OGB 2. Given
3. 3. Reflex. prop. 
4. ΔLBG  ΔOGB 4. SAS
5. L  O 5. CPCTC
L
B
O
G
,BL GO
BL GO
BG GB

13. Example Given:
Prove: O  R
To prove the angles congruent, we can
break this shape into two triangles, prove
the triangles congruent, and then use
CPCTC to prove the angles congruent.
R
U
O
F
,FO FR UO UR 

14. Example: Given:
Prove: O  R
R
U
O
F
Statements Reasons
1. 1. Given
2. 2. Given
3. 3. Refl. prop. 
4. ΔFOU  ΔFRU 4. SSS
5. O  R 5. CPCTC
FO FR
UO UR
UF UF
,FO FR UO UR 