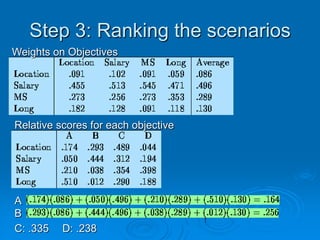
The Analytic Hierarchy Process (AHP) is a decision-making tool that breaks down complex decisions into a series of pairwise comparisons. It allows decision makers to incorporate both qualitative and quantitative factors. The AHP works by: 1) Computing weights for each decision criterion through pairwise comparisons. 2) Scoring alternatives based on each criterion. 3) Multiplying the weights and scores to obtain overall scores for each alternative. 4) Ranking the alternatives based on their overall scores. Consistency is also checked to ensure reliable results. An example is provided to illustrate the AHP process.

1. Analytic Hierarchy
Process
Zheng-Wen Shen
2006/04/11

2. Outline
1. Introduction of AHP
2. How the AHP works
3. Example

3. 1. Introduction of AHP
Is job Salary is
1 best ? important
..
Is Job Location
2 best ? is
important..
Is Job Long term
3 best ? prospect is
important..
Is Job
4 best ? Interest is
important..
Crystal is looking for job…

4. AHP Features
 AHPis a powerful tool that may be used to
make decisions when
 multiple and conflicting objectives/criteria are
present,
 and both qualitative and quantitative aspects
of a decision need to be considered.
 AHP reduces complex decisions to a
series of pairwise comparisons.

5. 2. How the AHP works
1. Computing the vector of objective
weights
2. Computing the matrix of scenario scores
3. Ranking the scenarios
4. Checking the consistency
consider m evaluation criteria and n scenarios.

6. AHP Steps
1. Computing the vector of objective
weights
2. Computing the matrix of scenario scores
3. Ranking the scenarios
4. Checking the consistency

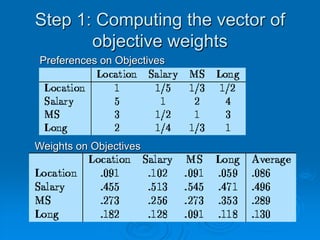
7. Step 1: Computing the vector of
objective weights
 Pairwisecomparison matrix A [m × m].
 Each entry ajk of A represents the
importance of criterion j relative to criterion
k:
 If ajk > 1, j is more important than k
 if ajk < 1, j is less important than k
 if ajk = 1, same importance
 ajk and akj must satisfy ajkakj = 1.

8. Step 1: Computing the vector of
objective weights
 The relative importance between two criteria is
measured according to a numerical scale from 1
to 9.
 A  Anorm (Normalized)

9. Step 1: Computing the vector of
objective weights
Preferences on Objectives
Weights on Objectives

10. AHP Steps
1. Computing the vector of objective
weights
2. Computing the matrix of scenario scores
3. Ranking the scenarios
4. Checking the consistency

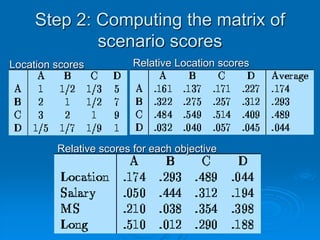
11. Step 2: Computing the matrix of
scenario scores
 The matrix of scenario scores S [n × m]
 Each entry sij of S represents the score of the
scenario i with respect to the criterion j
 The score matrix S is obtained by the columns sj
calculated as follows:
 A pairwise comparison matrix Bj is built for each
criterion j.
 Each entry bjih represents the evaluation of the
scenario i compared to the scenario h with respect to
the criterion j according to the DM’s evaluations.
 From each matrix Bj a score vectors sj is obtained (as
in Step 1).

12. Step 2: Computing the matrix of
scenario scores
Location scores Relative Location scores
Relative scores for each objective

13. AHP Steps
1. Computing the vector of objective
weights
2. Computing the matrix of scenario scores
3. Ranking the scenarios
4. Checking the consistency

14. Step 3: Ranking the scenarios
 Once the weight vector w and the score matrix S
have been computed, the AHP obtains a vector
v of global scores by multiplying S and w
 v = S · w.
 The i-th entry vi of v represents the global score
assigned by the AHP to the scenario i
 The scenario ranking is accomplished by
ordering the global scores in decreasing order.

15. Step 3: Ranking the scenarios
Weights on Objectives
Relative scores for each objective
A
B
C: .335 D: .238

16. AHP Steps
1. Computing the vector of objective
weights
2. Computing the matrix of scenario scores
3. Ranking the scenarios
4. Checking the consistency

17. Step 4: Checking the consistency
 When many pairwise comparisons are
performed, inconsistencies may arise.
 criterion 1 is slightly more important than
criterion 2
 criterion 2 is slightly more important than
criterion 3
 inconsistency arises if criterion 3 is more
important than criterion 1

18. Step 4: Checking the consistency
 The Consistency Index (CI) is obtained:
 x is the ratio of the j-th element of the vector
A · w to the corresponding element of the
vector w
 CI is the average of the x
A perfectly consistent DM should always
obtain CI = 0
 but inconsistencies smaller than a given
threshold are tolerated.

19. 3. Example (1/7)
 Small
example, m = 3 criteria and n = 3
scenarios.
0 S3 S2 S1
Criterion 1
0 S1 S3 S2
Criterion 2
0 S3 S2 S1
Criterion 3

20. Example (2/7)
 pairwise comparison matrix A for the 3
criteria
 Weight Vector

21. Example (3/7)
 pairwise scenario comparison matrices for
the first criterion:
 Score Vector

22. Example (4/7)
 pairwise scenario comparison matrices for
the first criterion:
 Score Vector

23. Example (5/7)
 pairwise scenario comparison matrices for
the first criterion:
 Score Vector

24. Example (6/7)
 Score Matrix S is :
 Global Score Vector

25. Example (7/7)
 The rank is:
 Scenario 1: 0.523
 Scenario 2: 0.385
 Scenario 3: 0.092