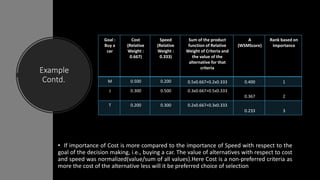
The weighted sum method (WSM) is a multi-criteria decision-making technique used to evaluate alternatives based on various criteria, requiring all data to be in the same unit. This method assigns relative weights to each criterion and calculates a score for each alternative by aggregating these weighted values. An example illustrates its application in choosing a car, demonstrating how to prioritize cost and speed with normalized values.

1. Weighted Sum Method
Dr. Mrinmoy Majumder
Course Name : Intro to Multi Criteria Decision Making Methods
Lecture No.09 out of 15
https://opticlasses.teachable.com
Follow me on :
RG : Mrinmoy Majumder
Twitter : kuttu80
Founding Honorary Editor
http://www.baipatra.ws
http://www.energyinstyle.website

2. What is Weighted Sum Method
• In decision making problems, the Weighted Sum Model or
Method(WSM) (Fishburn et.al.,1967) is the simplest known multi-
criteria decision making(MCDM) method for evaluating a number of
alternatives in terms of a number of decision criteria.
• Applicable only when all the data are in exactly the same unit.
Let wj describe the relative weight of significance of the criterion Cj and aij is the performance value or
normalized magnitude of alternative Ai when it is evaluated in terms of criterion Cj. Then, the total (i.e.,
when all the criteria are considered simultaneously) importance of alternative Ai, denoted as Ai
WSM-score
Reference : Fishburn, P.C. (1967). "Additive Utilities with Incomplete Product Set: Applications to Priorities
and Assignments". Operations Research Society of America (ORSA), Baltimore, MD, U.S.A.

3. How it
Works ?

4. Example of
ANP
Decision Goal : To buy a car
Criteria : Cost and Speed
Alternatives : Mercedes Benz(M),
Jaguar(J), Toyota(T)
Aggregation Methods to be used :
Weighted Sum Method

5. Example
Contd.
• If importance of Cost is more compared to the importance of Speed with respect to the
goal of the decision making, i.e., buying a car. The value of alternatives with respect to cost
and speed was normalized(value/sum of all values).Here Cost is a non-preferred criteria as
more the cost of the alternative less will it be preferred choice of selection
Goal :
Buy a
car
Cost
(Relative
Weight :
0.667)
Speed
(Relative
Weight :
0.333)
Sum of the product
function of Relative
Weight of Criteria and
the value of the
alternative for that
criteria
A
(WSMScore)
Rank based on
importance
M 0.500 0.200 0.5x0.667+0.2x0.333 0.400 1
J 0.300 0.500 0.3x0.667+0.5x0.333
0.367 2
T 0.200 0.300 0.2x0.667+0.3x0.333
0.233 3