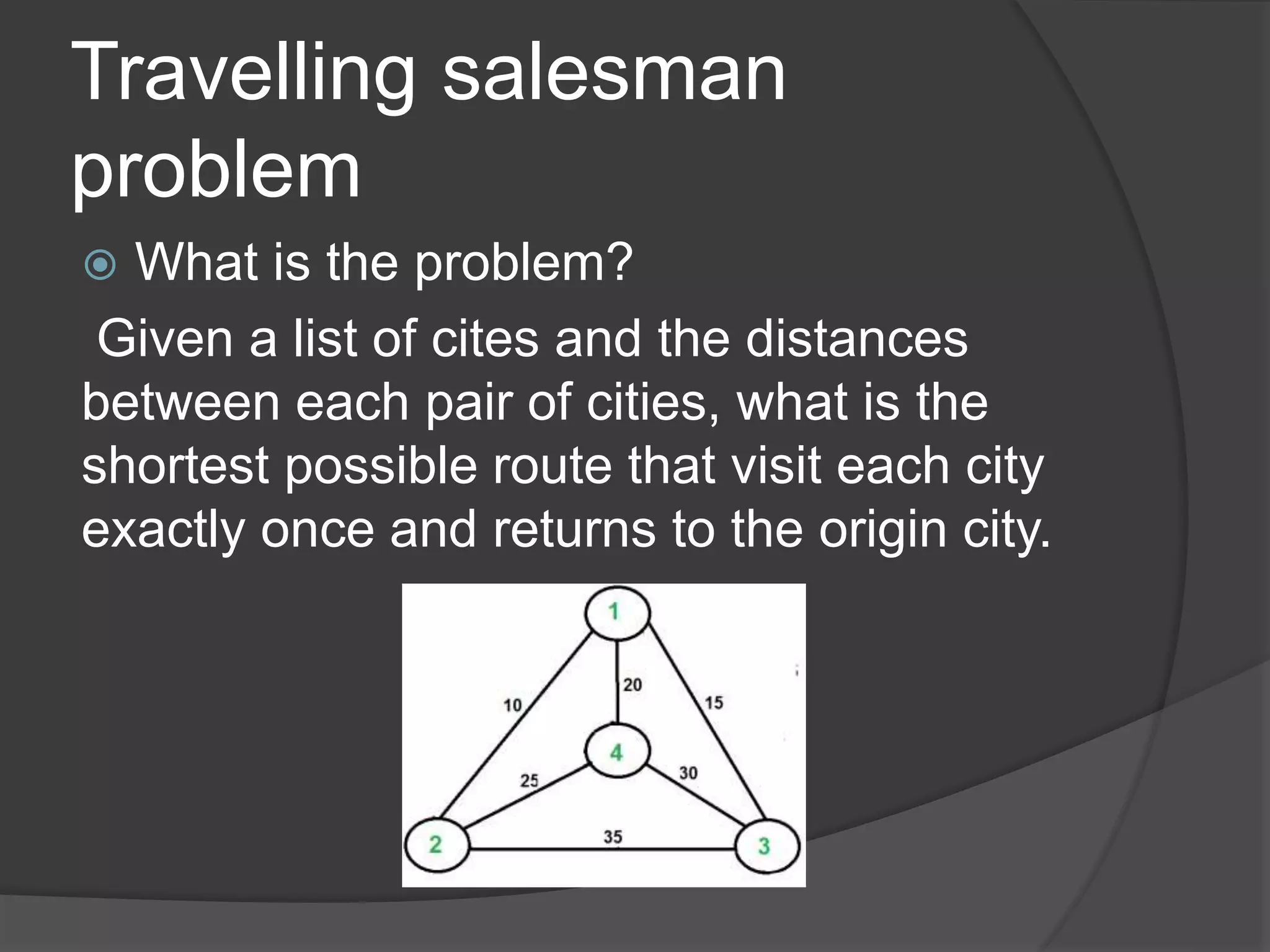
This document discusses methods for solving the travelling salesman problem, specifically focusing on the Hungarian method. It provides an overview of the travelling salesman problem and describes several algorithms to solve it, including genetic algorithms, branch and bound, and dynamic programming. It then explains the Hungarian method in more detail, outlining the algorithm's steps to find an optimal assignment with minimum cost by drawing lines through rows and columns to cover zero entries in the cost matrix. The advantages of the Hungarian method for solving travelling salesman problems are highlighted, along with its time complexity of O(n^3).

1. Artificial intelligence
Group members
Hamza Haseeb(14)
Harmain Haider(23)

2. content
 Travelling salesman problem?
 Methods to solve this problem
 Hungarian method
 Advantages of Hungarian method
 Time complexity

3. Travelling salesman
problem
 What is the problem?
Given a list of cites and the distances
between each pair of cities, what is the
shortest possible route that visit each city
exactly once and returns to the origin city.

4. Methods to solve
 Genetic algorithm
 Branch and bound method
 Dynamic programming
 Optimal solution
 Heuristic algorithm
 Hungarian method

5. Hungarian method
 The Hungarian method is an algorithm
which finds an optimal assignment for a
given cost matrix.

6. Algorithm
 Step 1. Subtract the smallest entry in each row from all
the entries of its row.
 Step 2. Subtract the smallest entry in each column from
all the entries of its column.
 Step 3. Draw lines through appropriate rows and columns
so that all the zero entries of the cost matrix are covered
and the minimum number of such lines is used.
 Step 4. Test for Optimality: (i) If the minimum number of
covering lines is n, an optimal assignment of zeros is
possible and we are finished. (ii) If the minimum number
of covering lines is less than n, an optimal assignment of
zeros is not yet possible. In that case, proceed to Step 5.
 Step 5. Determine the smallest entry not covered by any
line. Subtract this entry from each uncovered row, and
then add it to each covered column. Return to Step 3.

7. Advantages of Hungarian
method
 Hungarian method provides optimal
solution for travelling salesman problem
with minimum cost to travel to all cities
only once and travel back to the origin
city
 It is also used in assignment problems
for example: If there are different tasks
and many employees and you want to
assign them tasks.

8. Time complexity
 The time complexity of the original
algorithm was O(n^4).
 But it is later modified to O(n^3) and it is
difficult to implement than O(n^4)
algorithm.