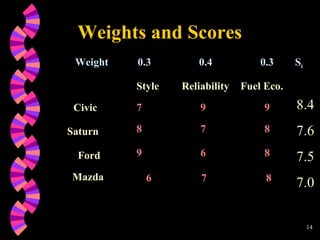
The document discusses multi-criteria decision making (MCDM) approaches, emphasizing the complexity of modern decision-making that often involves multiple objectives, such as safety and cost in public sector decisions. It outlines methods like the Weighted Score Method and the TOPSIS method for evaluating options based on various criteria through systematic processes. Examples provided include selecting a car and the wife selection problem, illustrating how different criteria impact decision outcomes.

1. Multi-Criteria Decision Making MCDM Approaches

2. Introduction Zeleny (1982) opens his book “Multiple Criteria Decision Making” with a statement: “ It has become more and more difficult to see the world around us in a unidimensional way and to use only a single criterion when judging what we see”

3. Introduction Many public sector problems and even private decision involve multiple objectives and goals. As an example: Locating a nuclear power plant involves objectives such as: Safety Health Environment Cost

4. Examples of Multi-Criteria Problems In a case study on the management of R&D research (Moore et. al 1976) , the following objectives have been identified: Profitability Growth and diversity of the product line Increased market share Maintained technical capability Firm reputation and image Research that anticipates competition

5. Examples of Multi-Criteria Problems In determining an electric route for power transmission in a city, several objectives could be considered: Cost Health Reliability Importance of areas

6. Examples of Multi-Criteria Problems In selecting a major at KFUPM, several objectives can be considered. These objectives or criteria include: Job market upon graduation Job pay and opportunity to progress Interest in the major Likelihood of success in the major Future job image Parent wish

7. Examples of Multi-Criteria Problems Wife selection problem . This problem is a good example of multi-criteria decision problem. Criteria include: Religion Beauty Wealth Family status Family relationship Education

8. Approaches For MCDM Several approaches for MCDM exist. We will cover the following: Weighted score method ( Section 5.1 in text book). TOPSIS method Analytic Hierarchy Process (AHP) Goal programming ?

9. Weighted score method Determine the criteria for the problem Determine the weight for each criteria. The weight can be obtained via survey, AHP, etc. Obtain the score of option i using each criteria j for all i and j Compute the sum of the weighted score for each option .

10. Weighted score method In order for the sum to make sense all criteria scale must be consistent, i.e., More is better or less is better for all criteria Example: In the wife selection problem , all criteria (Religion, Beauty, Wealth, Family status, Family relationship, Education) more is better If we consider other criteria (age, dowry) less is better

11. Weighted score method Let S ij score of option i using criterion j w j weight for criterion j S i score of option i is given as: S i =  w j S ij j The option with the best score is selected.

12. Weighted Score Method The method can be modified by using U(S ij ) and then calculating the weighted utility score. To use utility the condition of separability must hold. Explain the meaning of separability: U(S i ) =  w j U(S ij ) U(S i )  U(  w j S ij )

13. Example Using Weighted Scoring Method Objective Selecting a car Criteria Style, Reliability, Fuel-economy Alternatives Civic Coupe, Saturn Coupe, Ford Escort, Mazda Miata

14. Weights and Scores Weight 0.3 0.4 0.3 S i Civic Mazda 6 7 8 8.4 7.6 7.5 7.0 Style Reliability Fuel Eco. Saturn Ford 7 9 9 8 7 8 9 6 8

15. TOPSIS METHOD T echnique of O rder P reference by S imilarity to I deal S olution This method considers three types of attributes or criteria Qualitative benefit attributes/criteria Quantitative benefit attributes Cost attributes or criteria

16. TOPSIS METHOD In this method two artificial alternatives are hypothesized : Ideal alternative : the one which has the best level for all attributes considered. Negative ideal alternative : the one which has the worst attribute values. TOPSIS selects the alternative that is the closest to the ideal solution and farthest from negative ideal alternative.

17. Input to TOPSIS TOPSIS assumes that we have m alternatives (options) and n attributes/criteria and we have the score of each option with respect to each criterion. Let x ij score of option i with respect to criterion j We have a matrix X = (x ij ) m  n matrix. Let J be the set of benefit attributes or criteria (more is better) Let J ' be the set of negative attributes or criteria (less is better)

18. Steps of TOPSIS Step 1: Construct normalized decision matrix. This step transforms various attribute dimensions into non-dimensional attributes, which allows comparisons across criteria. Normalize scores or data as follows: r ij = x ij / (  x 2 ij ) for i = 1, …, m; j = 1, …, n i

19. Steps of TOPSIS Step 2: Construct the weighted normalized decision matrix. Assume we have a set of weights for each criteria w j for j = 1,…n. Multiply each column of the normalized decision matrix by its associated weight. An element of the new matrix is: v ij = w j r ij

20. Steps of TOPSIS Step 3: Determine the ideal and negative ideal solutions. Ideal solution. A* = { v 1 * , …, v n * }, where v j * ={ max (v ij ) if j  J ; min (v ij ) if j  J ' } i i Negative ideal solution. A' = { v 1 ' , …, v n ' }, where v' = { min (v ij ) if j  J ; max (v ij ) if j  J ' } i i

21. Steps of TOPSIS Step 4: Calculate the separation measures for each alternative. The separation from the ideal alternative is: S i * = [  (v j * – v ij ) 2 ] ½ i = 1, …, m j Similarly, the separation from the negative ideal alternative is: S ' i = [  ( v j ' – v ij ) 2 ] ½ i = 1, …, m j

22. Steps of TOPSIS Step 5: Calculate the relative closeness to the ideal solution C i * C i * = S ' i / (S i * +S ' i ) , 0  C i *  1 Select the option with C i * closest to 1. WHY ?

23. Applying TOPSIS Method to Example Weight 0.1 0.4 0.3 0.2 Civic Mazda 6 7 8 6 Cost Style Reliability Fuel Eco. Saturn Ford 7 9 9 8 8 7 8 7 9 6 8 9

24. Applying TOPSIS to Example m = 4 alternatives (car models) n = 4 attributes/criteria x ij = score of option i with respect to criterion j X = {x ij } 4  4 score matrix. J = set of benefit attributes: style, reliability, fuel economy (more is better) J ' = set of negative attributes: cost (less is better)

25. Steps of TOPSIS Step 1(a): calculate (  x 2 ij ) 1/2 for each column Style Rel. Fuel Saturn Ford 49 81 81 64 64 49 64 49 81 36 64 81 Civic Mazda Cost  x ij 2 i (  x 2 ) 1/2 36 49 64 36 230 215 273 230 15.17 14.66 16.52 15.17

26. Steps of TOPSIS Step 1 (b): divide each column by (  x 2 ij ) 1/2 to get r ij Style Rel. Fuel Saturn Ford 0.46 0.61 0.54 0.53 0.53 0.48 0.48 0.46 0.59 0.41 0.48 0.59 Civic Mazda 0.40 0.48 0.48 0.40 Cost

27. Steps of TOPSIS Step 2 (b): multiply each column by w j to get v ij . Style Rel. Fuel Saturn Ford 0.046 0.244 0.162 0.106 0.053 0.192 0.144 0.092 0.059 0.164 0.144 0.118 Civic Mazda 0.040 0.192 0.144 0.080 Cost

28. Steps of TOPSIS Step 3 (a): determine ideal solution A*. A* = {0.059, 0.244, 0.162, 0.080} Style Rel. Fuel Saturn Ford 0.046 0.244 0.162 0.106 0.053 0.192 0.144 0.092 0.059 0.164 0.144 0.118 Civic Mazda 0.040 0.192 0.144 0.080 Cost

29. Steps of TOPSIS Step 3 (a): find negative ideal solution A ' . A ' = {0.040, 0.164, 0.144, 0.118} Style Rel. Fuel Saturn Ford 0.046 0.244 0.162 0.106 0.053 0.192 0.144 0.092 0.059 0.164 0.144 0.118 Civic Mazda 0.040 0.192 0.144 0.080 Cost

30. Steps of TOPSIS Step 4 (a): determine separation from ideal solution A* = {0.059, 0.244, 0.162, 0.080} S i * = [  (v j * – v ij ) 2 ] ½ for each row j Style Rel. Fuel Saturn Ford (.046 -.059 ) 2 (.244 -.244 ) 2 (0) 2 (.026) 2 Civic Mazda Cost (.053 -.059 ) 2 (.192 -.244 ) 2 (-.018) 2 (.012) 2 (.053 -.059 ) 2 (.164 -.244 ) 2 (-.018) 2 (.038) 2 (.053 -.059 ) 2 (.192 -.244 ) 2 (-.018) 2 (.0) 2

31. Steps of TOPSIS Step 4 (a): determine separation from ideal solution S i *  (v j * –v ij ) 2 S i * = [  (v j * – v ij ) 2 ] ½ Saturn Ford 0.000845 0.029 0.003208 0.057 0.008186 0.090 Civic Mazda 0.003389 0.058

32. Steps of TOPSIS Step 4 (b): find separation from negative ideal solution A ' = {0.040, 0.164, 0.144, 0.118} S i ' = [  (v j ' – v ij ) 2 ] ½ for each row j Style Rel. Fuel Saturn Ford (.046 -.040 ) 2 (.244 -.164 ) 2 (.018) 2 (-.012) 2 Civic Mazda Cost (.053 -.040 ) 2 (.192 -.164 ) 2 (0) 2 (-.026) 2 (.053 -.040 ) 2 (.164 -.164 ) 2 (0) 2 (0) 2 (.053 -.040 ) 2 (.192 -.164 ) 2 (0) 2 (-.038) 2

33. Steps of TOPSIS Step 4 (b): determine separation from negative ideal solution S i '  (v j ' –v ij ) 2 S i ' = [  (v j ' – v ij ) 2 ] ½ Saturn Ford 0.006904 0.083 0.001629 0.040 0.000361 0.019 Civic Mazda 0.002228 0.047

34. Steps of TOPSIS Step 5: Calculate the relative closeness to the ideal solution C i * = S ' i / (S i * +S ' i ) S ' i /(S i * +S ' i ) C i * Saturn Ford 0.083/0.112 0.74  BEST 0.040/0.097 0.41 0.019/0.109 0.17 Civic Mazda 0.047/0.105 0.45