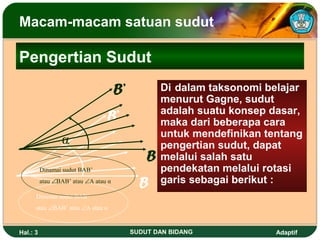
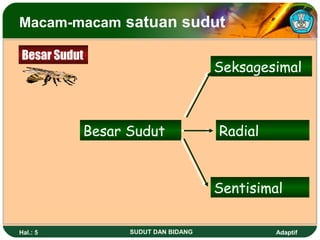
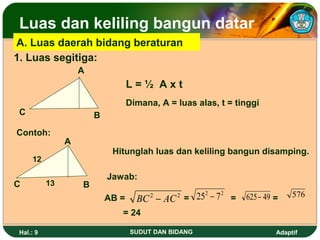
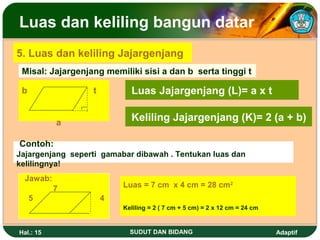
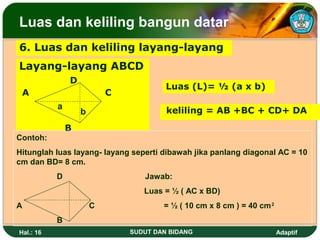
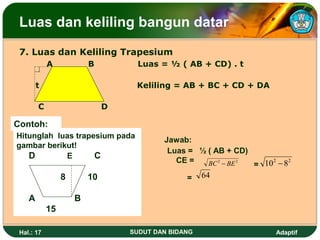
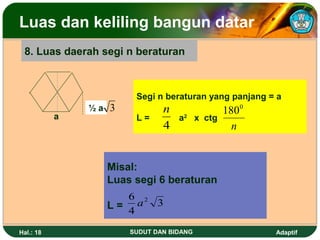
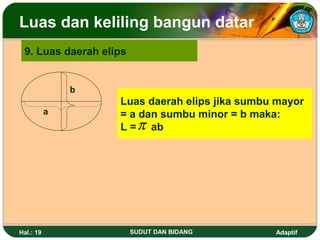
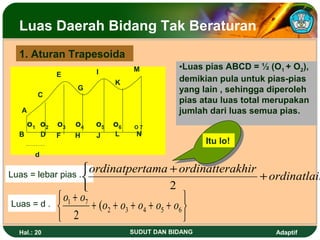
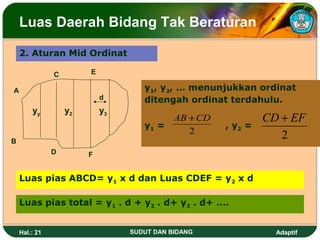
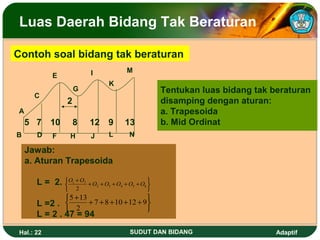
Dokumen ini membahas tentang sudut dan bidang serta cara menentukan kedudukan garis dan besar sudut dalam dimensi dua. Juga dijelaskan berbagai satuan ukuran sudut seperti derajat, radian, dan grad serta rumus untuk menghitung luas dan keliling berbagai bangun datar seperti segitiga, persegi, dan lingkaran. Terdapat pula cara menghitung luas bidang tak beraturan menggunakan metode trapesoida dan mid ordinat.

1. SUDUT DAN
BIDANG
Mengidentifikasi Sudut

2. SUDUT DAN BIDANG
Standar Kompetensi:
Menentukan kedudukan garis, dan besar sudut yang
melibatkan titik, garis dan bidang dalam dimensi dua
Kompetensi Dasar:
1. Mengidentifikasi south.
2. Menentukan keliling bangun datar dan luas bangun
datar.
3. Menerapkan transformasi bangun datar.
Hal.: 2 SUDUT DAN BIDANG Adaptif

3. Macam-macam satuan sudut
Pengertian Sudut
B’ Di dalam taksonomi belajar
menurut Gagne, sudut
adalah suatu konsep dasar,
B’ maka dari beberapa cara
untuk mendefinikan tentang
α pengertian sudut, dapat
B melalui salah satu
Dinamai sudut BAB’ pendekatan melalui rotasi
atau ∠BAB’ atau ∠A atau α
B garis sebagai berikut :
Dinamai sudut BAB’
atau ∠BAB’ atau ∠A atau α
Hal.: 3 SUDUT DAN BIDANG Adaptif

4. Macam-macam satuan sudut
Sudut Dalam Kedudukan Baku
Y
C
θ
θ
Sudut θ tidak dlm X
A
kedudukan baku
Sudut θ dalam kedudukan baku
Sisi AB disebut sisi permulaan dari sudut θ
Sisi AC disebut sisi batas dari sudut θ
Hal.: 4 SUDUT DAN BIDANG Adaptif

5. Macam-macam satuan sudut
Besar Sudut
Seksagesimal
Besar Sudut Radial
Sentisimal
Hal.: 5 SUDUT DAN BIDANG Adaptif

6. Macam-macam satuan sudut
Sistem Sebagai motivasi diceriterakan bahwa
Radial untuk pengukuran sudut elevasi
penembakan meriam dalam kemiliteran
zaman dulu diperlukan ukuran sudut yang
tidak menggunakan ukuran derajat, namun
ukuran lain yang lazim kita kenal dengan
istilah sistem radian
Dalam sistem radian yang dimaksud besar
1 radian sudut satu radian adalah besar sudut pusat
r
dari suatu lingkaran yang panjang busur
dihadapan sudut tersebut adalah sama
dengan jari-jari lingkaran tersebut.
Sehingga diperoleh hubungan:
1800 = π radian
1 radian ≈ 57,296 0 ≈ 57 017'45"
10 ≈ 0,017453 radian
Hal.: 6 SUDUT DAN BIDANG Adaptif

7. Macam-macam satuan sudut
Sistem Sentisimal
 Pada instrumen-instrumen untuk keperluan
astronomi, peneropongan bintang, teodolit
dikenal satuan sudut yang sedikit berlainan
dengan kedua ukuran di atas, sistem ini kita
kenal dengan nama sistem sentisimal. Pada
sistem ini satu putaran penuh adalah 400g
(dibaca “400 grad”).
 Sehingga besar sudut ½ putaran adalah 200g
besar sudut ¼ putaran adalah 100g
besar sudut 1/400 putaran
adalah 1g
Untuk ukuran sudut yang lebih kecil dikenal :
 1g = 10dgr = 10 (dibaca : “10 decigrad”)
 1dgr = 10cgr = 10 (dibaca : “10
centigrad”)
 1cgr = 10 mgr = 10 (dibaca : “10 miligrad”)
 1mgr = 10 dmgr = 10 (dibaca : “10
decimiligrad”)
Hal.: 7 SUDUT DAN BIDANG Adaptif

8. Konversi Sudut
Konversi satuan sudut
Satuan derajad = satuan radian = grad
3600 =2 π radian = 400g
1 radian = 57,3250 = 63,694g
10 = 0,0174 radian = 1,11g
1g = 0,90 = 0,0157 radian
1° = 60’ = 3600” detik
Contoh:
Ubahlah 300 kedalam satuan radian dan grade!
Jawab:
300 = 30 x 0,0174 radian = 0,522 radian
300 = 30 x 1,11 g = 33,3 g
Hal.: 8 SUDUT DAN BIDANG Adaptif

9. Luas dan keliling bangun datar
A. Luas daerah bidang beraturan
1. Luas segitiga:
A
L=½ Axt
Dimana, A = luas alas, t = tinggi
C B
Contoh:
A
Hitunglah luas dan keliling bangun disamping.
12
Jawab:
C 13 B
AB = BC − AC =
2 252 − 7 2 =
2 625 − 49 = 576
= 24
Hal.: 9 SUDUT DAN BIDANG Adaptif

10. Luas dan keliling bangun datar
Lanjutan!
Luas segitiga: Keliling segitiga:
a×t K = AB + BC+ AC = 13 cm + 12 cm
L= +5
2
AB × AC 24× 7
= = = 84
2 2
Jadi,luas segitiga tersebut adalah 84 cm2 dan kelilingnya 56 cm
1.1 Jika segitiga memiliki sisi a, b, c dan tinggi segitiga yang tegak
lurus alas adalah t maka:
A
b Atau L = s( s − a )( s − b)( s − c)
c
C t ¬ a +b +c
B Dengan s =
a 2
a×t Keliling (K)= a + b + c
Luas segitiga (L) =
2
Hal.: 10 SUDUT DAN BIDANG Adaptif

11. The width and circumference of
flat plane
Next!
Triangle width: Triangle circumference:
a×t K = AB + BC+ AC = 13 cm + 12 cm
L= +5
2
AB × AC 24× 7
= = = 84
2 2
So, the triangle width is 84 cm2 and the circumference is 56 cm
1.1 If the triangle has side a, b, c and triangle high that base right
stand is t, then:
A
b Or L = s( s − a )( s − b)( s − c)
c
C t ¬ a +b +c
B With s =
a 2
a×t Circumference (K)= a + b + c
Triangle width (L) =
2
Hal.: 11 SUDUT DAN BIDANG Adaptif

12. I Luas dan keliling bangun datar
2. LUAS PERSEGI
Rumus untuk luas setiap persegi adalah:
Luas = panjang sisi x panjang sisi
L =sxs
L = s2
Keliling (K) = 4 x sisi
Hal.: 12 SUDUT DAN BIDANG Adaptif

13. Luas dan keliling beliling bangun datar
3. Luas dan keliling lingkaran
Rumus untuk luas setiap lingkaran adalah:
Luas = π x jari-jari x jari-jari
=πxrxr
Dengan
= πr2 π = 3,14
Atau
Keliling lingkaran = 2 π r π=
Hal.: 13 SUDUT DAN BIDANG Adaptif

14. Luas dan keliling bangun datar
4. Luas dan keliling persegi panjang
Persegi panjang ABCD Luas ABCD = p x 
A p B
Keliling ABCD = (2 x p) + ( 2 x )

C D
Contoh:
Persegi panjang ABCD dengan panjang 8 cm dan lebar 6 cm.
Tentukan luas dan keliling persegi panjang tersebut !
Jawab:
Luas persegi panjang = p x  = 8 x 6 = 48
Keliling persegi panjang = (2 x p) + (2 x )
= (2 x 8) + ( 2 x 6)
= 16 + 12
= 28
Hal.: 14 SUDUT DAN BIDANG Adaptif

15. Luas dan keliling bangun datar
5. Luas dan keliling Jajargenjang
Misal: Jajargenjang memiliki sisi a dan b serta tinggi t
b t Luas Jajargenjang (L)= a x t
a
Keliling Jajargenjang (K)= 2 (a + b)
Contoh:
Jajargenjang seperti gamabar dibawah . Tentukan luas dan
kelilingnya!
Jawab:
7 Luas = 7 cm x 4 cm = 28 cm2
5 4
Keliling = 2 ( 7 cm + 5 cm) = 2 x 12 cm = 24 cm
Hal.: 15 SUDUT DAN BIDANG Adaptif

16. Luas dan keliling bangun datar
6. Luas dan keliling layang-layang
Layang-layang ABCD
D
Luas (L)= ½ (a x b)
A C
a keliling = AB +BC + CD+ DA
b
B
Contoh:
Hitunglah luas layang- layang seperti dibawah jika panlang diagonal AC = 10
cm dan BD= 8 cm.
D Jawab:
Luas = ½ ( AC x BD)
A C = ½ ( 10 cm x 8 cm ) = 40 cm 2
B
Hal.: 16 SUDUT DAN BIDANG Adaptif

17. Luas dan keliling bangun datar
7. Luas dan Keliling Trapesium
A B Luas = ½ ( AB + CD) . t
t Keliling = AB + BC + CD + DA
C D
Contoh:
Hitunglah luas trapesium pada
Jawab:
gambar berikut!
Luas = ½ ( AB + CD)
D E C CE =
= 10 − 8
2 2
BC 2 − BE 2
8 10 = 64
A B
15
Hal.: 17 SUDUT DAN BIDANG Adaptif

18. Luas dan keliling bangun datar
8. Luas daerah segi n beraturan
Segi n beraturan yang panjang = a
½a 3 n 1800
a L= a2 x ctg
4 n
Misal:
Luas segi 6 beraturan
6 2
L= 4a 3
Hal.: 18 SUDUT DAN BIDANG Adaptif

19. Luas dan keliling bangun datar
9. Luas daerah elips
b
Luas daerah elips jika sumbu mayor
a = a dan sumbu minor = b maka:
L = π ab
Hal.: 19 SUDUT DAN BIDANG Adaptif

20. Luas Daerah Bidang Tak Beraturan
1. Aturan Trapesoida
M •Luas pias ABCD = ½ (O1 + O2),
E I
K demikian pula untuk pias-pias
G yang lain , sehingga diperoleh
C
pias atau luas total merupakan
A jumlah dari luas semua pias.
o 1 o2 o3 o4 o 5 o6 O7
B D F H J L N
Itu lo!
d
Luas = lebar pias . 
ordinatpertama + ordinatterakhir
 + ordinatlain
 2
 o1 + o7 
Luas = d .
 + (o2 + o3 + o4 + o5 + o6 
 2 
Hal.: 20 SUDUT DAN BIDANG Adaptif

21. Luas Daerah Bidang Tak Beraturan
2. Aturan Mid Ordinat
C E
A y1, y2, … menunjukkan ordinat
d ditengah ordinat terdahulu.
yy y2 y3
AB + CD CD + EF
y1 = , y2 =
2
B
2
D F
Luas pias ABCD= y1 x d dan Luas CDEF = y2 x d
Luas pias total = y1 . d + y2 . d+ y3 . d+ ….
Hal.: 21 SUDUT DAN BIDANG Adaptif

22. Luas Daerah Bidang Tak Beraturan
Contoh soal bidang tak beraturan
I M
E
K
G Tentukan luas bidang tak beraturan
C
2 disamping dengan aturan:
A a. Trapesoida
5 7 10 8 12 9 13 b. Mid Ordinat
B D F H J L N
Jawab:
a. Aturan Trapesoida
L = 2.  O1 + O7 
 + O2 + O3 + O4 + O5 + O6 
 2 
 5 + 13 
L =2 .  + 7 + 8 + 10 + 12 + 9
 2 
L = 2 . 47 = 94
Hal.: 22 SUDUT DAN BIDANG Adaptif

23. Luas Daerah Bidang Tak Beraturan
Lanjutan
b. Aturan Mid Ordinat
y1 = 5 + 7 = 6 , y2 =
7 + 10
= 8,5 , y3=
10 + 8 , y4= 8 + 12 = 10
=8
2 2 2 2
12 + 9 9+3
y5= = 10,5 , y6 = =6
2 2
Luas Total = y1 .d + y2. d+ y3. d + y4. d+ y5. d+ y6. d
= 6 . 2 + 8,5. 2 + 8 . 2 + 10 . 2+ 10,5 . 2 + 6 . 2
= 12 + 17 + 16 + 20 + 21 + 12
= 98
Hal.: 23 SUDUT DAN BIDANG Adaptif

24. Terima kasih
Giatlah untuk terus
berlatih..berlatih..
dan berlatih…
SEKIAN
Hal.: 24 SUDUT DAN BIDANG Adaptif