Downloaded 419 times
Uploaded byJen Soriano
IGCSE Pysics Momentum
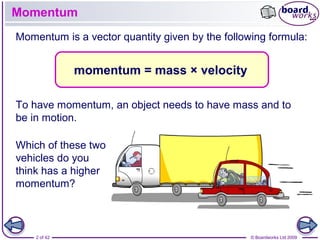
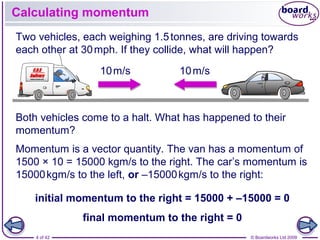
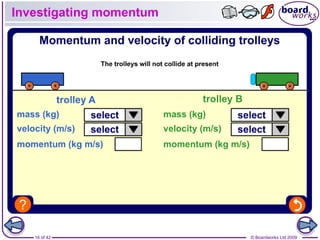
This document discusses momentum and its relationship to mass and velocity. It defines momentum as being equal to mass multiplied by velocity, and explains that momentum is a vector quantity. It also discusses impulse, which is defined as the change in momentum, and explains how impulse is related to force and time through the equation: Impulse = Force x Time. The document notes that momentum is always conserved during interactions and collisions.
More Related Content
Similar to IGCSE Pysics Momentum
IGCSE Pysics Momentum
- 1. 1 of 42© Boardworks Ltd 2009
- 2. 2 of 42© Boardworks Ltd 2009 Momentum Momentum is a vector quantity given by the following formula: To have momentum, an object needs to have mass and to be in motion. momentum = mass × velocity Which of these two vehicles do you think has a higher momentum?
- 3. 3 of 42© Boardworks Ltd 2009
- 4. 4 of 42© Boardworks Ltd 2009 Calculating momentum Momentum is a vector quantity. The van has a momentum of 1500 × 10 = 15000 kgm/s to the right. The car’s momentum is 15000kgm/s to the left, or –15000kgm/s to the right: 10m/s 10m/s Two vehicles, each weighing 1.5tonnes, are driving towards each other at 30mph. If they collide, what will happen? Both vehicles come to a halt. What has happened to their momentum? initial momentum to the right = 15000 + –15000 = 0 final momentum to the right = 0
- 5. 5 of 42© Boardworks Ltd 2009 Momentum calculations
- 6. 6 of 42© Boardworks Ltd 2009
- 7. 7 of 42© Boardworks Ltd 2009 If the resultant force acting on an object is not zero, all the forces are said to be unbalanced. This forms the basis of Newton’s second law of motion, which states: What is Newton’s second law? If the forces on an object are unbalanced, two things about the object can change: the speed of the object may change – it may either increase or decrease the direction of motion may change.
- 8. 8 of 42© Boardworks Ltd 2009 What is impulse? Newton’s second law in the form F = Δ(mv) / Δt can be rearranged to give: FΔt = Δ(mv) The quantity FΔt is the impulse of the force, so it can be seen that impulse = change in momentum Impulse is a vector quantity with the same direction as the force. It is measured in newton seconds (Ns). The impulse of a force is defined as: impulse = FΔt Note that Ns are the same as kgms–1 as expected since impulse = Δ(mv), but Ns are usually used for impulse.
- 9. 9 of 42© Boardworks Ltd 2009 Impulse and collisions The size of force controls how much damage there is. Look at the equation for impulse. What determines how much damage is done in a collision, and how can it be reduced? FΔt = Δ(mv) Momentum is conserved in a collision, so impulse is constant. To reduce the force, the time over which the collision takes place should be increased.
- 10. 10 of 42© Boardworks Ltd 2009
- 11. 11 of 42© Boardworks Ltd 2009 Conservation of momentum initial momentum final momentum = Momentum is always conserved in any event or interaction: When a snooker ball collides with another, what happens to the momentum of each ball? What happens when a car brakes and comes to a halt, or when a rock falls to the ground and stops? Momentum is transferred to the Earth. Momentum is not created or lost, but transferred from one object to the other.
- 12. 12 of 42© Boardworks Ltd 2009 Explosions and recoil Remember: momentum is always conserved. What happens to the momentum in the following situations?
- 13. 13 of 42© Boardworks Ltd 2009 Explosions and recoil Remember: momentum is always conserved. What happens to the momentum in the following situations? Explain in terms of the momentum of the fuel being expelled from the rocket.
- 14. 14 of 42© Boardworks Ltd 2009 Explosions and recoil Remember: momentum is always conserved. What happens to the momentum in the following situations? the idea of recoil: the ground does not visibly move when the basketball player jumps, but it must carry an equal and opposite momentum.
- 15. 15 of 42© Boardworks Ltd 2009 Explosions and recoil Remember: momentum is always conserved. What happens to the momentum in the following situations? Direction in momentum calculations: all parts of the fireworks have much higher speeds after they explode, but their directions cancel out and momentum is conserved.
- 16. 16 of 42© Boardworks Ltd 2009 Investigating momentum
- 17. 17 of 42© Boardworks Ltd 2009 Multiple-choice quiz
- 18. 18 of 42© Boardworks Ltd 2009 Anagrams
Editor's Notes
- #3 Teacher notes This question should lead to discussion as it is not clear from the picture which vehicle has the higher momentum. The lorry has a higher mass than the car, but the car is moving at a greater velocity.
- #9 Teacher notes If a pair of equal and opposite forces act for the same time period, their changes in momentum are also equal and opposite. This is a way of stating Newton’s third law in terms of momentum.
- #10 Photo credit: © Shutterstock 2010, John C. Panella Jr.
- #13 Teacher notes This slide should encourage discussion. Students could be encouraged to explain the first picture in terms of the momentum of the fuel being expelled from the rocket. The second picture introduces the idea of recoil: the ground does not visibly move when the basketball player jumps, but it must carry an equal and opposite momentum. The third picture further emphasizes the importance of direction in momentum calculations: all parts of the fireworks have much higher speeds after they explode, but their directions cancel out and momentum is conserved. Photo credit (all): © 2009 Jupiterimages Corporation
- #14 Teacher notes This slide should encourage discussion. Students could be encouraged to explain the first picture in terms of the momentum of the fuel being expelled from the rocket. The second picture introduces the idea of recoil: the ground does not visibly move when the basketball player jumps, but it must carry an equal and opposite momentum. The third picture further emphasizes the importance of direction in momentum calculations: all parts of the fireworks have much higher speeds after they explode, but their directions cancel out and momentum is conserved. Photo credit (all): © 2009 Jupiterimages Corporation
- #15 Teacher notes This slide should encourage discussion. Students could be encouraged to explain the first picture in terms of the momentum of the fuel being expelled from the rocket. The second picture introduces the idea of recoil: the ground does not visibly move when the basketball player jumps, but it must carry an equal and opposite momentum. The third picture further emphasizes the importance of direction in momentum calculations: all parts of the fireworks have much higher speeds after they explode, but their directions cancel out and momentum is conserved. Photo credit (all): © 2009 Jupiterimages Corporation
- #16 Teacher notes This slide should encourage discussion. Students could be encouraged to explain the first picture in terms of the momentum of the fuel being expelled from the rocket. The second picture introduces the idea of recoil: the ground does not visibly move when the basketball player jumps, but it must carry an equal and opposite momentum. The third picture further emphasizes the importance of direction in momentum calculations: all parts of the fireworks have much higher speeds after they explode, but their directions cancel out and momentum is conserved. Photo credit (all): © 2009 Jupiterimages Corporation
- #17 Teacher notes This virtual experiment enables students to explore how mass and velocity affect the momentum of an object, and how momentum is conserved in a collision. Select a mass and velocity for each trolley, then click the momentum box to reveal the momentum of each trolley, or ask students to calculate the value first. Once the trolleys have collided, students could be encouraged to calculate the total momentum and velocity of the combined trolleys, before revealing the final values and the working for the calculations.
- #18 Teacher notes This multiple-choice quiz could be used as a plenary activity to assess students’ understanding of forces and motion. The questions can be skipped through without answering by clicking “next”. Students could be asked to complete the questions in their books and the activity could be concluded by completion on the IWB.