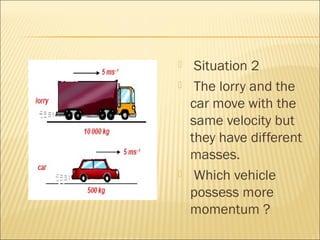
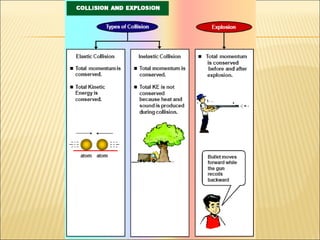
Momentum is defined as the product of an object's mass and velocity. The principle of conservation of momentum states that the total momentum of a system remains constant if no external forces act on it. Applications include collisions between objects like cars and the jet propulsion of airplanes, where hot gases ejected from the back provide an equal and opposite momentum to push the plane forward.