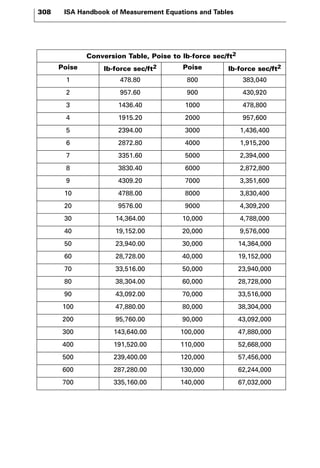
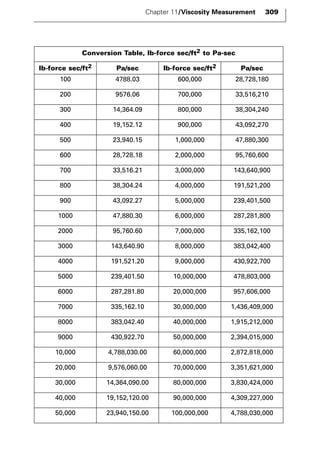
This document provides information about viscosity measurement including: - Definitions of viscosity, dynamic viscosity, kinematic viscosity, and their units. Common units include poise, centipoise, stoke, and centistoke. - Methods for measuring viscosity including the Hagen-Poiseuille law relating flow rate to viscosity in a tube, and Stokes' law relating drag force on a sphere to viscosity. - Tables converting between different viscosity units like poise, Pa-s, and lb-force-sec/ft2, and values for viscometer constants used in some viscosity calculations.

1. 11
VISCOSITY
MEASUREMENT
Principles of Viscosity & Definitions . . . . . . . . . . . . . . . . . . . . . . . . 301
Viscosity SI Units . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 301
Dynamic, Absolute, or Simple Viscosity . . . . . . . . . . . . . . . . . . . . . 302
Kinematic Viscosity . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 302
Common Viscosity Units . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 303
Other Viscosity Equations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 304
Measuring Viscosity. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 305
Hagen-Poiseuille’s Law . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 305
Stoke’s Law. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 305
Values of Viscometer Constants A and B . . . . . . . . . . . . . . . . . . . . 306
Viscosity Conversion Tables . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 307
Poise to lb-force sec/ft2 Conversion Table . . . . . . . . . . . . . . . . . . . . 308
lb-force sec/ft2 to Pa-sec Conversion Table . . . . . . . . . . . . . . . . . . . 309

2. Chapter 11/Viscosity Measurement 301
Principles of Viscosity & Definitions
Viscosity is a quantity describing a fluid’s resistance to flow. Fluids
resist the relative motion of immersed objects through them as well as
to the motion of layers with differing velocities within them.
Formally, viscosity (represented by the symbol η) is the ratio of the
shearing stress (F/A) to the velocity gradient (Δvx/Δz or dvx/dz) in a fluid.


÷ 
x x Δ
Δ
 
F
A
v
z
η = η
 
 
= 
 
÷ 
 
or
F
A
dv
dz
The more usual form of this relationship is called “Newton’s equation.”
It states the resulting shear of a fluid is directly proportional to the force
applied and inversely proportional to its viscosity. Note the similarity to
Newton’s second law of motion (F = ma).
F
A
Δ
Δ
v
z
F
A
dv
dz
= x = x
η η
or
Δ
Δ
= =
F m
v
t
F m
dv
dt






Viscosity SI Units
According to NIST’s Guide for the International System of Units (SI), the
proper SI units for expressing values of viscosity η (also called
dynamic viscosity) and values of kinematic viscosity ν are, respectively,
the Pascal second (Pa·s) and the meter squared per second (m2/s) (and
their decimal multiples and submultiples as appropriate).
The Pascal second [Pa·s] has no special name. And, although touted as
an international system, the International System of Units (SI) has had
very little international impact. The Pascal second is rarely used in sci-entific
and technical publications today.
The most common unit of viscosity is the dyne second per square
centimeter (dyne · s/cm2), which is given the name poise (P) after the
French physiologist Jean Louis Poiseuille (1799-1869). Ten poise equal
one Pascal second (Pa·s) making the centipoise (cP) and millipascal
second (mPa·s) identical.

3. 302 ISA Handbook of Measurement Equations and Tables
1 Pascal second = 10 poise = 1,000 millipascal second
1 centipoise = 1 millipascal second
English/Metric Viscosity Units
Quantity English Metric
Viscosity Poise Pa/sec
Kinematic
Stroke m2/sec
Viscosity
There are actually two quantities called viscosity. The quantity defined
above usually is just called viscosity. However, it sometimes is also
called dynamic viscosity, absolute viscosity, or simple viscosity to dis-tinguish
it from the other quantity.
Dynamic, Absolute, or Simple Viscosity
a t = −
V At
B
where
Va = dynamic, absolute, or simple viscosity
A = a viscometer constant
B = a viscometer constant
t = time for a volume of fluid to pass through an aperture
Kinematic Viscosity
The other quantity, called kinematic viscosity (represented by the sym-bol
ν), is the ratio of the viscosity of a fluid to its density.
v =
η
ρ
Kinematic viscosity is a measure of the resistive flow of a fluid under
the influence of gravity. It is frequently measured by a “capillary
viscometer” — basically a graduated can with a narrow tube at the bot-tom.
When two fluids of equal volume are placed in identical capillary
viscometers and allowed to flow under the influence of gravity, a
viscous fluid takes longer than a less viscous fluid to flow through the
tube.

4. where
Kv = kinematic viscosity
V = viscosity of fluid
D = density of fluid
Chapter 11/Viscosity Measurement 303
Kv
The SI unit of kinematic viscosity is the square meter per second (m2/s),
which also has no special name. This unit is so large it is rarely used. A
more common unit of kinematic viscosity is the square centimeter per
second (cm2/s), which has been given the name stoke [St] after the Eng-lish
scientist George Stoke. Since this unit is also large, the more com-monly
used unit is the square millimeter per second (mm2/s) or centis-toke
(cSt).
According to NIST’s Guide for the International System of Units (SI), the
CGS units commonly used to express values of these quantities, the
poise (P) and the stokes (St), respectively [and their decimal submulti-ples
the centipoise (cP) and the centistoke (cSt)], are not to be used.
However, since CGS units are, in fact, the most widely used terms, they
are included in this ISA Handbook.
2
mCommon Viscosity Units
1 m2/s = 10,000 cm2/s (stoke) = 1,000,000 mm2/s (centistokes)
1 c/s = 1 stoke
1 mm2
/s = 1 centistoke
1 Poise = 1 dyne sec/cm2
1 Poise = 0.1 Pa sec
1 Centipoise = 0.001 Pa/sec
1 Centipoise = 1 cm2/sec
1 cP = viscosity of water at 68°C
1 lb-force sec/ft2 = 1 slug/ft sec
V
D
=

5. 304 ISA Handbook of Measurement Equations and Tables
Other Viscosity Equations
V
where
V = viscosity of a fluid
Ss = shear stress, force per area
Sr = shear rate, velocity per layer thickness
Ratio of Shear Stress to Shear Rate, Hagen-Poiseuille Law
π 4
8
where
V = viscosity
Pd = pressure differential of liquid
R = inside radius of tube
Q = rate of liquid flow
L = length of tube
Apparent Viscosity (Consistency)
C
A
W
where
C = consistency, percent
Ad = dry-weight of solid
Ws = weight of solid plus liquid
d
s
= x 100
V
P R
QL
= d
S
S
s
r
=

6. Chapter 11/Viscosity Measurement 305
Measuring Viscosity
Hagen-Poiseuille’s Law
French physician and physiologist Jean Poiseuille, while developing an
improved method for measuring blood pressure, formulated a mathe-matical
expression for the flow rate for the laminar (nonturbulent) flow
of fluids in circular tubes. Discovered independently by Gotthilf Hagen,
a German hydraulic engineer, this relation is also known as the Hagen-
Poiseuille equation, or Hagen-Poiseuille Law.
For laminar, non-pulsatile fluid flow through a uniform straight pipe, the
flow rate (volume per unit time) is:
• directly proportional to the pressure difference between the
ends of the tube,
• inversely proportional to the length of the tube,
• inversely proportional to the viscosity of the fluid, and
• proportional to the fourth power of the radius of the tube.
φ
ΔPr4
8
π
η
=
Stoke’s Law
George Gabriel Stokes, an Irish-born mathematician who spent much of
his life working with fluid properties, is most famous for his work
describing the motion of a sphere through viscous fluids. This led to the
development of Stokes’s Law – an equation that shows the force
needed to move a small sphere through a continuous, quiescent fluid at
a certain velocity. It is based primarily on the radius of the sphere
and the viscosity of the fluid. He found what has become known as
Stokes’ Law:
The drag force on a sphere of radius (R) moving through a fluid of vis-cosity
η at speed Vc is given by:
F(drag) = 6πRηVc
Where
R = the radius of the sphere
η = the viscosity
Vc = the velocity through a continuous fluid
The faster a sphere falls through a fluid, the lower the viscosity. The
measurement involves dropping a sphere through a measured
distance of fluid and measuring how long it takes to traverse the distance.

7. 306 ISA Handbook of Measurement Equations and Tables
Since you know distance and time, you also know velocity, which is dis-tance/
time. A formula for determining the viscosity in this manner is:
viscosity
Δp
9v
2( )ga2
= η =
Where
Δp = difference in density between the sphere and the liquid
g = acceleration of gravity
a = radius of sphere
v = velocity = d/t = (Distance sphere falls/time it takes to fall)
Values of Viscometer Constants A and B
Viscometer Constant A Constant B Time of Efflux
Saybolt Universal 0.226
0.220
195
135
32-100
over 100
Saybolt Furol 2.24 184 25-40
Redwood #1 0.260
0.247
179
50
34-100
over 100
Redwood #2 2.46
2.45
100
-
32-90
over 90

8. Chapter 11/Viscosity Measurement 307
Viscosity Conversion Table
To Convert from To Multiply by:
Centipoise Pascal/sec 0.001
Centistroke m2/sec 0.000001
cm3/sec ft3/min 0.00211888
cm3/sec liter/hr 3.6
ft3/hr cm3/sec 7.865791
ft3/hr liter/min 0.4719474
ft3/min cm3/sec 471.9474
ft3/sec cm3/hr 101.9406
ft3/sec liter/min 1699.011
in3/min cm3/sec 0.2731177
Dyne-sec/cm2 Poise 1.0
Geepound Slug 1.0
Gram-force Dyne 980.665
kilogram-force Dyne 0.0000980665
liter/sec ft3/hr 127.1328
liter/sec ft3/min 2.11888
liter/sec gallon/hr 951.0194
part per million mg/kg 1.0
part per million ml/cm3 1.0
Poise Dyne-sec/cm2 1.0
Poise gram/cm-sec 1.0
Poise Pascal-sec 0.1
lb-force-sec/ft2 Pascal-sec 47.8803
lb-force-sec/in2 Pascal-sec 6894.76
Slug kg 14.5939

9. 308 ISA Handbook of Measurement Equations and Tables
Conversion Table, Poise to lb-force sec/ft2
Poise lb-force sec/ft2 Poise lb-force sec/ft2
1 478.80 800 383,040
2 957.60 900 430,920
3 1436.40 1000 478,800
4 1915.20 2000 957,600
5 2394.00 3000 1,436,400
6 2872.80 4000 1,915,200
7 3351.60 5000 2,394,000
8 3830.40 6000 2,872,800
9 4309.20 7000 3,351,600
10 4788.00 8000 3,830,400
20 9576.00 9000 4,309,200
30 14,364.00 10,000 4,788,000
40 19,152.00 20,000 9,576,000
50 23,940.00 30,000 14,364,000
60 28,728.00 40,000 19,152,000
70 33,516.00 50,000 23,940,000
80 38,304.00 60,000 28,728,000
90 43,092.00 70,000 33,516,000
100 47,880.00 80,000 38,304,000
200 95,760.00 90,000 43,092,000
300 143,640.00 100,000 47,880,000
400 191,520.00 110,000 52,668,000
500 239,400.00 120,000 57,456,000
600 287,280.00 130,000 62,244,000
700 335,160.00 140,000 67,032,000

10. Chapter 11/Viscosity Measurement 309
Conversion Table, lb-force sec/ft2 to Pa-sec
lb-force sec/ft2 Pa/sec lb-force sec/ft2 Pa/sec
100 4788.03 600,000 28,728,180
200 9576.06 700,000 33,516,210
300 14,364.09 800,000 38,304,240
400 19,152.12 900,000 43,092,270
500 23,940.15 1,000,000 47,880,300
600 28,728.18 2,000,000 95,760,600
700 33,516.21 3,000,000 143,640,900
800 38,304.24 4,000,000 191,521,200
900 43,092.27 5,000,000 239,401,500
1000 47,880.30 6,000,000 287,281,800
2000 95,760.60 7,000,000 335,162,100
3000 143,640.90 8,000,000 383,042,400
4000 191,521.20 9,000,000 430,922,700
5000 239,401.50 10,000,000 478,803,000
6000 287,281.80 20,000,000 957,606,000
7000 335,162.10 30,000,000 1,436,409,000
8000 383,042.40 40,000,000 1,915,212,000
9000 430,922.70 50,000,000 2,394,015,000
10,000 4,788,030.00 60,000,000 2,872,818,000
20,000 9,576,060.00 70,000,000 3,351,621,000
30,000 14,364,090.00 80,000,000 3,830,424,000
40,000 19,152,120.00 90,000,000 4,309,227,000
50,000 23,940,150.00 100,000,000 4,788,030,000