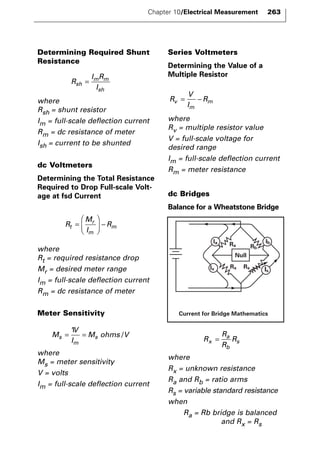
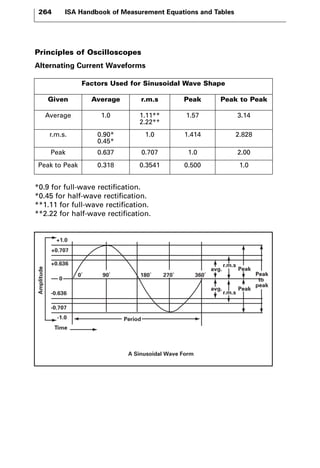
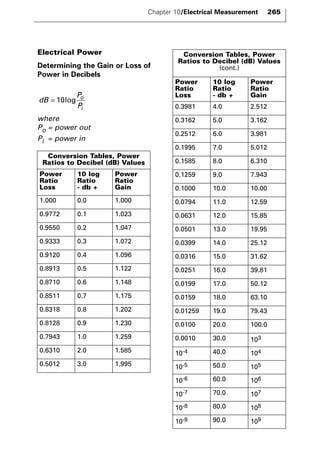
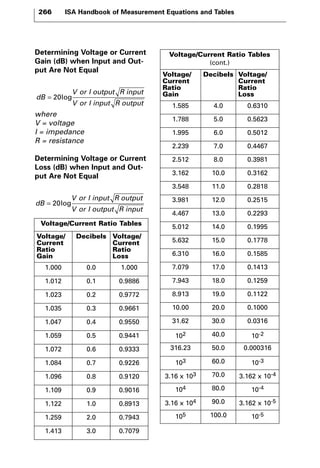
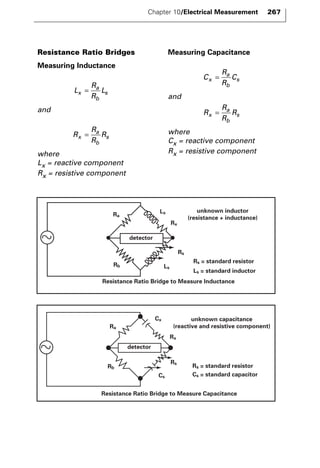
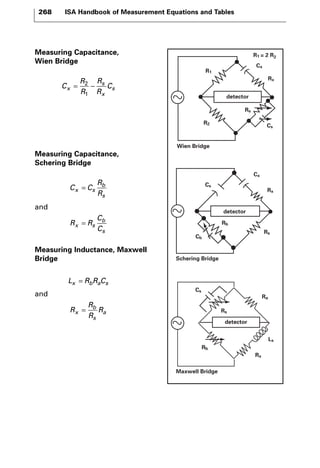
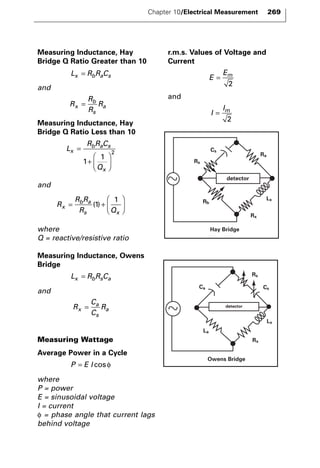
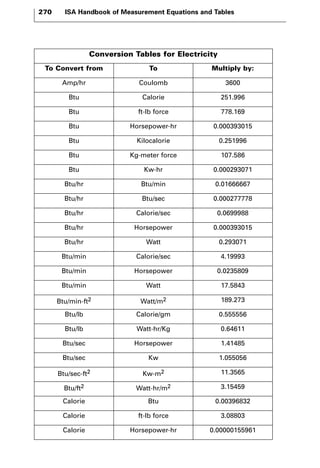
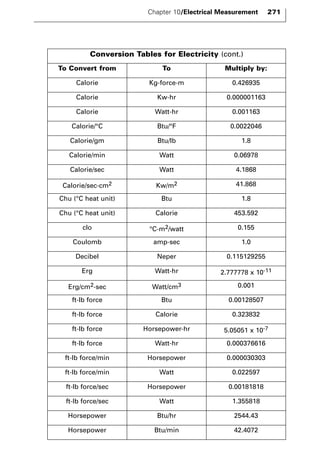
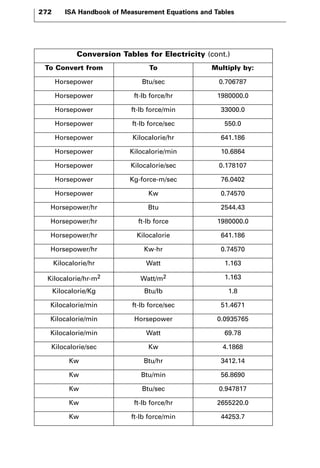
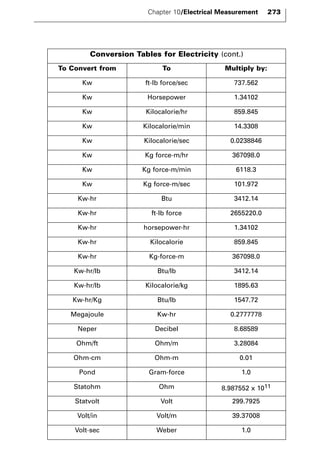
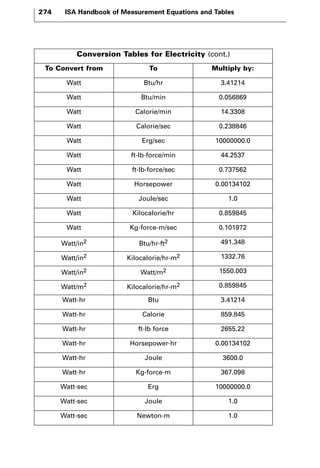
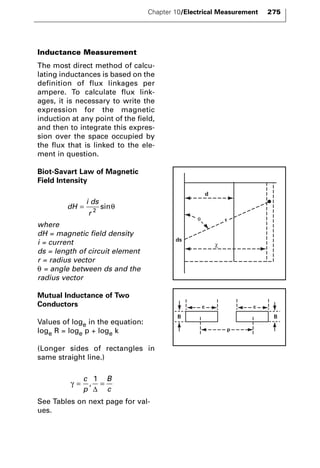
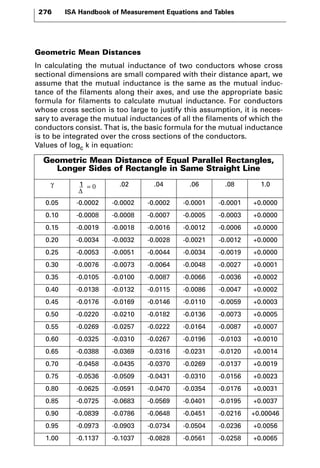
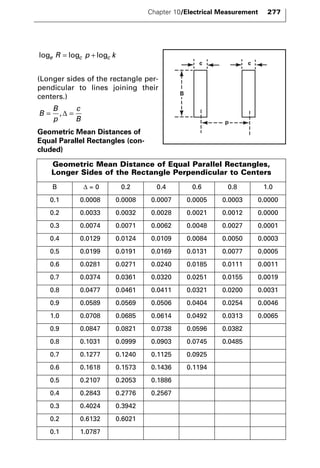
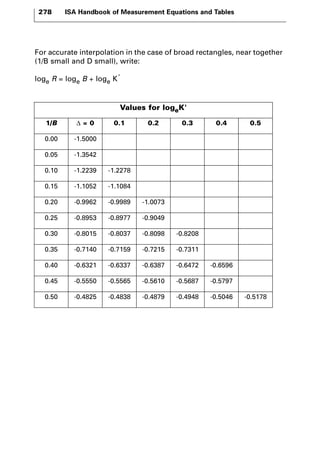
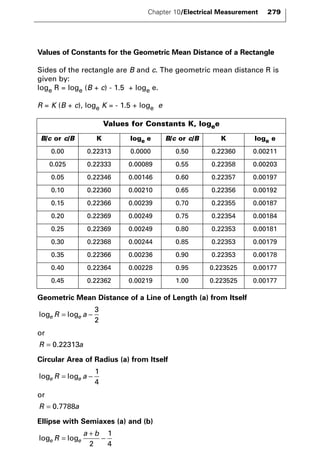
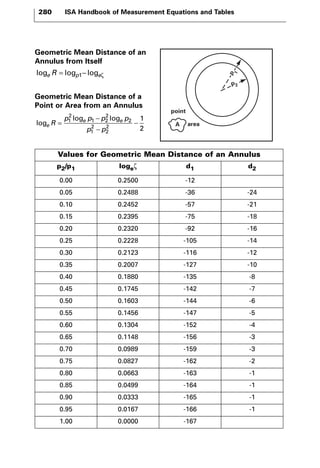
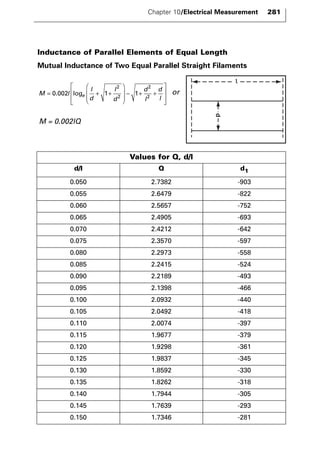
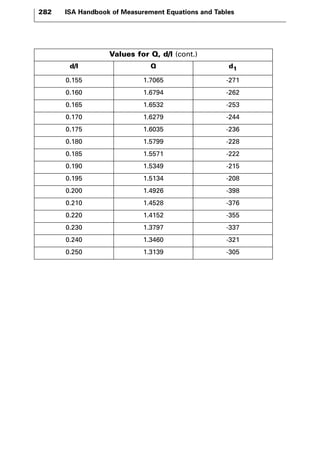
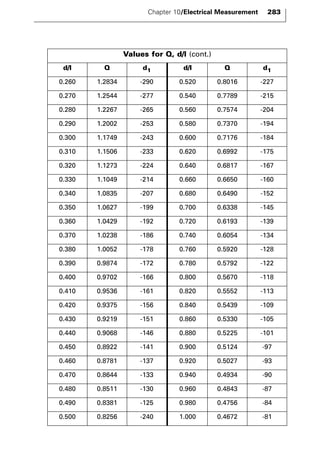
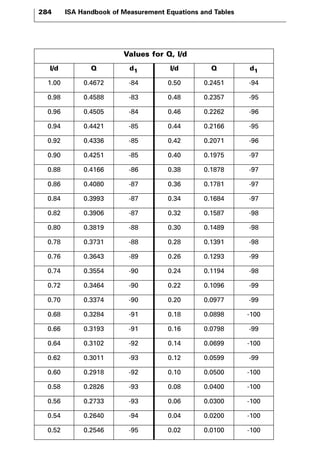
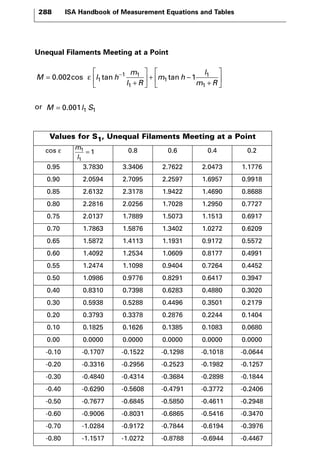
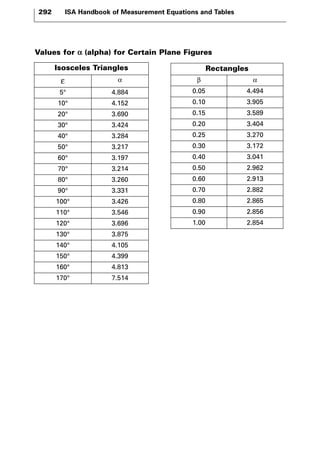
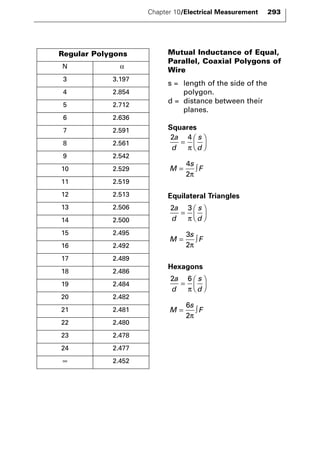
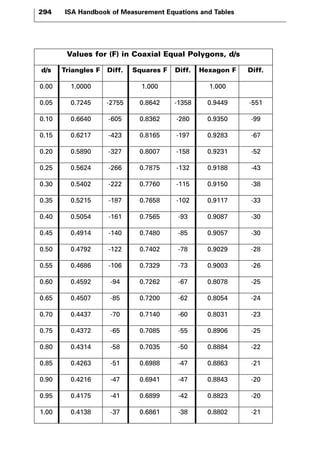
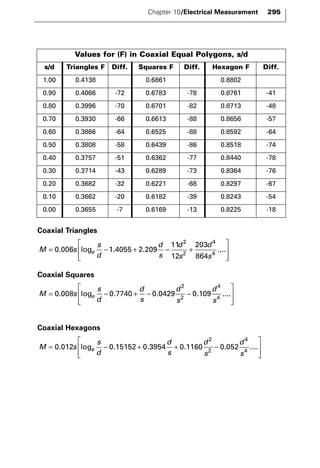
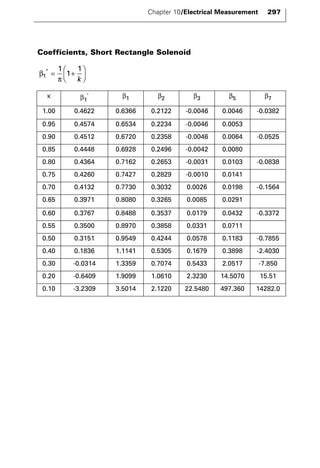
The document discusses various principles and methods of electrical measurement. It provides equations and diagrams for measuring resistance, capacitance, inductance, voltage, current, power and more using techniques like Wheatstone bridges, Schering bridges and other circuits. Measurement concepts covered include Ohm's law, reactance, impedance, decibels, peak vs RMS values, and how to calculate unknown values using ratio and balance methods with standard resistors.

1. 10
Electrical Measurement
Principles of Electrical Measurement. . . . . . . . . . . . . . . . . . . . . . . . 261
Principles of Oscilloscopes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 264
Electrical Power . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 265
Voltage Ratios. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 266
Resistance Ratio Bridges. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 267
Electricity Conversions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 270
Inductance Measurement.. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 275
Geometric Mean Distances . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 276
Values for Q . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 281
Mutual Inductance . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 285
Self Inductance. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 285, 298

2. Principles of Electrical Measurement
Resistance
Ω = V
AT
T( )
where
Ω = resistance
V = voltage
AT = ampere turns
T = turns
Ampere Turns
Amperes
AT
A
where
A = amperes
V
= T
Ω
( )
AT =
Ω
Direct Current
The Universal (Arytron) Shunt
For 0 to 10 mA, use:
0.009 (Rsh1 +Rsh2 +Rsh3) = 0.001(Rm)
where
Rsh1 = 0.111 ohm shunt
Rsh2 = 1.11 ohm shunt
Rsh3 = 11.1 ohm shunt
Rm = 100
For 10.01 to 100 mA, use:
99 (Rsh2 +Rsh3) = 1(Rm +Rsh1)
For 100.01 mA to 1 amp, use:
999 (Rsh3) = 1(Rm +Rsh1 +Rsh2)
Chapter 10/Electrical Measurement 261
Rm = 100
Rsh3
M
10 mA Configuration
Rsh2 Rsh1
Rm = 100
Rsh2
Rsh1
Rm = 100
9/
1/
Rsh1
Rsh2
99/ 1/
999/
Rsh3
M
100 mA Configuration
1/
Rsh3
M
1 amp Configuration
The Universal (Arytron) Shunt

3. 262 ISA Handbook of Measurement Equations and Tables
Ohm’s Law for Direct
Current
2
EI EI
2
P = power in watts
I = current in amperes
E = electromotive force in volts
R = resistance in ohms
Two resistances in parallel
combination:
= −
1 2
1 2
Any number of resistances in
parallel combination:
For calculating capacitance in
series combinations, substitute
C for R in the above equations.
Ohm’s Law for Alternating
Current
f
2
1
2
1
= = =
=
=
π LC 2 π CX
2
π
π
XL
L
2
2
1
2
XL f L
X
f C
L
1
2
π
XL
f f C
C
= =
π π
1
f X
c
c
=
2
π
2
2
( )
c
1
2 2
( )
f L
2 2 2 2
Z R X R XL X
Z RwhenXL X
where
Z = impedance in ohms
XL = inductive reactance in ohms
Xc = capacitive reactance in
ohms
L = inductance henrys
C = capacitance in farads
f = frequency in cycles per
second
2π f = 377 for 60 cps
c
c
=
= + = + −
= =
( )
π
1 = 1 + 1 +1
req R1 R2
Rn
req
R R
R R
+
P
E
I
R
P
Z
I
E
IR
IZ
E
R
E
P
E
P
E
Z
E
I
E
R
E
Z
I R 2 I R 2 P
E
P
E
P
I 2
P
I 2
P
I
P
I
PR
P
R
PZ
P
Z

4. Determining Required Shunt
Resistance
m m
sh
=
where
Rsh = shunt resistor
Im = full-scale deflection current
Rm = dc resistance of meter
Ish = current to be shunted
dc Voltmeters
Determining the Total Resistance
Required to Drop Full-scale Volt-age
at fsd Current
r
m

= m
where
Rt = required resistance drop
Mr = desired meter range
Im = full-scale deflection current
Rm = dc resistance of meter
Meter Sensitivity
= = s 1
where
Ms = meter sensitivity
V = volts
Im = full-scale deflection current
Series Voltmeters
Determining the Value of a
Multiple Resistor
= − m
where
Rv = multiple resistor value
V = full-scale voltage for
desired range
Im = full-scale deflection current
Rm = meter resistance
dc Bridges
Balance for a Wheatstone Bridge
Rb Ra
lb
lx ls
a
b
Rx Rs
la
= s
where
Rx = unknown resistance
Ra and Rb = ratio arms
Rs = variable standard resistance
when
Ra = Rb bridge is balanced
and Rx = Rs
R
R
R
x R
R
V
I
v R
m
M
V
I
s M ohms V
m
/
R
M
I
t R
 

 
−
R
I R
sh I
Chapter 10/Electrical Measurement 263
Null
Current for Bridge Mathematics

5. 264 ISA Handbook of Measurement Equations and Tables
Principles of Oscilloscopes
Alternating Current Waveforms
Factors Used for Sinusoidal Wave Shape
Given Average r.m.s Peak Peak to Peak
Average 1.0 1.11**
2.22**
*0.9 for full-wave rectification.
*0.45 for half-wave rectification.
**1.11 for full-wave rectification.
**2.22 for half-wave rectification.
1.57 3.14
r.m.s. 0.90*
0.45*
1.0 1.414 2.828
Peak 0.637 0.707 1.0 2.00
Peak to Peak 0.318 0.3541 0.500 1.0
+1.0
+0.707
+0.636
0
-0.636
-0.707
-1.0
Time
Amplitude
0° 90° 180° 270° 360°
Period
avg.
avg.
r.m.s
r.m.s
Peak
Peak
Peak
to
peak
A Sinusoidal Wave Form

6. Electrical Power
Determining the Gain or Loss of
Power in Decibels
dB
P
P
o
i
= 10log
where
Po = power out
Pi = power in
Conversion Tables, Power
Ratios to Decibel (dB) Values
(cont.)
Power
Ratio
Loss
10 log
Ratio
- db +
Power
Ratio
Gain
0.3981 4.0 2.512
0.3162 5.0 3.162
0.2512 6.0 3.981
0.1995 7.0 5.012
0.1585 8.0 6.310
0.1259 9.0 7.943
0.1000 10.0 10.00
0.0794 11.0 12.59
0.0631 12.0 15.85
0.0501 13.0 19.95
0.0399 14.0 25.12
0.0316 15.0 31.62
0.0251 16.0 39.81
0.0199 17.0 50.12
0.0159 18.0 63.10
0.01259 19.0 79.43
0.0100 20.0 100.0
0.0010 30.0 103
10-4 40.0 104
10-5 50.0 105
10-6 60.0 106
10-7 70.0 107
10-8 80.0 108
10-9 90.0 109
Conversion Tables, Power
Ratios to Decibel (dB) Values
Power
10 log
Power
Ratio
Ratio
Ratio
Loss
- db +
Gain
1.000 0.0 1.000
0.9772 0.1 1.023
0.9550 0.2 1.047
0.9333 0.3 1.072
0.9120 0.4 1.096
0.8913 0.5 1.122
0.8710 0.6 1.148
0.8511 0.7 1.175
0.8318 0.8 1.202
0.8128 0.9 1.230
0.7943 1.0 1.259
0.6310 2.0 1.585
0.5012 3.0 1.995
Chapter 10/Electrical Measurement 265

7. 266 ISA Handbook of Measurement Equations and Tables
Determining Voltage or Current
Gain (dB) when Input and Out-put
Are Not Equal
where
V = voltage
I = impedance
R = resistance
Determining Voltage or Current
Loss (dB) when Input and Out-put
Are Not Equal
dB
V or I input R output
V or I output R input
= 20log
dB
V or I output R input
V or I input R output
= 20log
Voltage/Current Ratio Tables
(cont.)
Voltage/
Current
Ratio
Gain
Decibels Voltage/
Current
Ratio
Loss
1.585 4.0 0.6310
1.788 5.0 0.5623
1.995 6.0 0.5012
2.239 7.0 0.4467
2.512 8.0 0.3981
3.162 10.0 0.3162
3.548 11.0 0.2818
3.981 12.0 0.2515
4.467 13.0 0.2293
5.012 14.0 0.1995
5.632 15.0 0.1778
6.310 16.0 0.1585
7.079 17.0 0.1413
7.943 18.0 0.1259
8.913 19.0 0.1122
10.00 20.0 0.1000
31.62 30.0 0.0316
102 40.0 10-2
316.23 50.0 0.000316
103 60.0 10-3
3.16 x 103 70.0 3.162 x 10-4
104 80.0 10-4
3.16 x 104 90.0 3.162 x 10-5
105 100.0 10-5
Voltage/Current Ratio Tables
Voltage/
Decibels Voltage/
Current
Current
Ratio
Ratio
Gain
Loss
1.000 0.0 1.000
1.012 0.1 0.9886
1.023 0.2 0.9772
1.035 0.3 0.9661
1.047 0.4 0.9550
1.059 0.5 0.9441
1.072 0.6 0.9333
1.084 0.7 0.9226
1.096 0.8 0.9120
1.109 0.9 0.9016
1.122 1.0 0.8913
1.259 2.0 0.7943
1.413 3.0 0.7079

8. Resistance Ratio Bridges
Measuring Inductance
and
R
R
a
b
= s
x L
a
b
= s
L
where
Lx = reactive component
Rx = resistive component
Measuring Capacitance
and
C
R
R
R
a
b
= s
x C
R
R
a
b
= s
x R
where
Cx = reactive component
Rx = resistive component
R
R
R
x R
Chapter 10/Electrical Measurement 267
detector
Lx
Rx
Ra
Rb Ls
Rs
unknown inductor
(resistance + inductance)
Rs = standard resistor
Ls = standard inductor
Resistance Ratio Bridge to Measure Inductance
Cx
(reactive and resistive component)
Rx
Ra
Rb
Cs
unknown capacitance
Rs Rs = standard resistor
Cs = standard capacitor
detector
Resistance Ratio Bridge to Measure Capacitance

9. 268 ISA Handbook of Measurement Equations and Tables
Measuring Capacitance,
Wien Bridge
s
x
= − s 2
Measuring Capacitance,
Schering Bridge
and
=
C C
b
s
x s R
=
R R
R
C
b
s
x s C
Measuring Inductance, Maxwell
Bridge
and
Lx = RbRaCs
R
R
R
b
s
= a
x R
C
R
R
R
R
x C
1
R2
Rs
Rs
Rs
Rb
Rx
Lx
Ra
Rb
Rx
Cx
Cs
Cs
Cb
Cs
Cx
Rx
R1
R1 = 2 R2
detector
detector
Wien Bridge
Schering Bridge
Maxwell Bridge
detector

10. Measuring Inductance, Hay
Bridge Q Ratio Greater than 10
and
Lx = RbRaCs
b
s
= a
Measuring Inductance, Hay
Bridge Q Ratio Less than 10
and

b a
s x
= +
 
where
Q = reactive/resistive ratio
Measuring Inductance, Owens
Bridge
and
Lx = RbRsCa
R
C
C
a
s
= a
x R
Measuring Wattage
Average Power in a Cycle
where
P = power
E = sinusoidal voltage
I = current
φ = phase angle that current lags
behind voltage
r.m.s. Values of Voltage and
Current
and
I
I = m
2
E
Em =
2
P = E I cosφ
R
R R
x R Q

 
(1)
1
L
R R C
Q
x
b a s
x
=
+

 

 
1
1 2
R
R
R
x R
Chapter 10/Electrical Measurement 269
detector
Lx
Rx
Rb
Rs
Cs
Ra
Hay Bridge
Rs
Cs
Lx
Rx
Ca
La
detector
Owens Bridge

11. 270 ISA Handbook of Measurement Equations and Tables
Conversion Tables for Electricity
To Convert from To Multiply by:
Amp/hr Coulomb 3600
Btu Calorie 251.996
Btu ft-lb force 778.169
Btu Horsepower-hr 0.000393015
Btu Kilocalorie 0.251996
Btu Kg-meter force 107.586
Btu Kw-hr 0.000293071
Btu/hr Btu/min 0.01666667
Btu/hr Btu/sec 0.000277778
Btu/hr Calorie/sec 0.0699988
Btu/hr Horsepower 0.000393015
Btu/hr Watt 0.293071
Btu/min Calorie/sec 4.19993
Btu/min Horsepower 0.0235809
Btu/min Watt 17.5843
Btu/min-ft2 Watt/m2 189.273
Btu/lb Calorie/gm 0.555556
Btu/lb Watt-hr/Kg 0.64611
Btu/sec Horsepower 1.41485
Btu/sec Kw 1.055056
Btu/sec-ft2 Kw-m2 11.3565
Btu/ft2 Watt-hr/m2 3.15459
Calorie Btu 0.00396832
Calorie ft-lb force 3.08803
Calorie Horsepower-hr 0.00000155961

12. Chapter 10/Electrical Measurement 271
Conversion Tables for Electricity (cont.)
To Convert from To Multiply by:
Calorie Kg-force-m 0.426935
Calorie Kw-hr 0.000001163
Calorie Watt-hr 0.001163
Calorie/°C Btu/°F 0.0022046
Calorie/gm Btu/lb 1.8
Calorie/min Watt 0.06978
Calorie/sec Watt 4.1868
Calorie/sec-cm2 Kw/m2 41.868
Chu (°C heat unit) Btu 1.8
Chu (°C heat unit) Calorie 453.592
clo °C-m2/watt 0.155
Coulomb amp-sec 1.0
Decibel Neper 0.115129255
Erg Watt-hr 2.777778 x 10-11
Erg/cm2-sec Watt/cm3 0.001
ft-lb force Btu 0.00128507
ft-lb force Calorie 0.323832
ft-lb force Horsepower-hr 5.05051 x 10-7
ft-lb force Watt-hr 0.000376616
ft-lb force/min Horsepower 0.000030303
ft-lb force/min Watt 0.022597
ft-lb force/sec Horsepower 0.00181818
ft-lb force/sec Watt 1.355818
Horsepower Btu/hr 2544.43
Horsepower Btu/min 42.4072

13. 272 ISA Handbook of Measurement Equations and Tables
Conversion Tables for Electricity (cont.)
To Convert from To Multiply by:
Horsepower Btu/sec 0.706787
Horsepower ft-lb force/hr 1980000.0
Horsepower ft-lb force/min 33000.0
Horsepower ft-lb force/sec 550.0
Horsepower Kilocalorie/hr 641.186
Horsepower Kilocalorie/min 10.6864
Horsepower Kilocalorie/sec 0.178107
Horsepower Kg-force-m/sec 76.0402
Horsepower Kw 0.74570
Horsepower/hr Btu 2544.43
Horsepower/hr ft-lb force 1980000.0
Horsepower/hr Kilocalorie 641.186
Horsepower/hr Kw-hr 0.74570
Kilocalorie/hr Watt 1.163
Kilocalorie/hr-m2 Watt/m2 1.163
Kilocalorie/Kg Btu/lb 1.8
Kilocalorie/min ft-lb force/sec 51.4671
Kilocalorie/min Horsepower 0.0935765
Kilocalorie/min Watt 69.78
Kilocalorie/sec Kw 4.1868
Kw Btu/hr 3412.14
Kw Btu/min 56.8690
Kw Btu/sec 0.947817
Kw ft-lb force/hr 2655220.0
Kw ft-lb force/min 44253.7

14. Chapter 10/Electrical Measurement 273
Conversion Tables for Electricity (cont.)
To Convert from To Multiply by:
Kw ft-lb force/sec 737.562
Kw Horsepower 1.34102
Kw Kilocalorie/hr 859.845
Kw Kilocalorie/min 14.3308
Kw Kilocalorie/sec 0.0238846
Kw Kg force-m/hr 367098.0
Kw Kg force-m/min 6118.3
Kw Kg force-m/sec 101.972
Kw-hr Btu 3412.14
Kw-hr ft-lb force 2655220.0
Kw-hr horsepower-hr 1.34102
Kw-hr Kilocalorie 859.845
Kw-hr Kg-force-m 367098.0
Kw-hr/lb Btu/lb 3412.14
Kw-hr/lb Kilocalorie/kg 1895.63
Kw-hr/Kg Btu/lb 1547.72
Megajoule Kw-hr 0.2777778
Neper Decibel 8.68589
Ohm/ft Ohm/m 3.28084
Ohm-cm Ohm-m 0.01
Pond Gram-force 1.0
Statohm Ohm 8.987552 x 1011
Statvolt Volt 299.7925
Volt/in Volt/m 39.37008
Volt-sec Weber 1.0

15. 274 ISA Handbook of Measurement Equations and Tables
Conversion Tables for Electricity (cont.)
To Convert from To Multiply by:
Watt Btu/hr 3.41214
Watt Btu/min 0.056869
Watt Calorie/min 14.3308
Watt Calorie/sec 0.238846
Watt Erg/sec 10000000.0
Watt ft-lb-force/min 44.2537
Watt ft-lb-force/sec 0.737562
Watt Horsepower 0.00134102
Watt Joule/sec 1.0
Watt Kilocalorie/hr 0.859845
Watt Kg-force-m/sec 0.101972
Watt/in2 Btu/hr-ft2 491.348
Watt/in2 Kilocalorie/hr-m2 1332.76
Watt/in2 Watt/m2 1550.003
Watt/m2 Kilocalorie/hr-m2 0.859845
Watt-hr Btu 3.41214
Watt-hr Calorie 859.845
Watt-hr ft-lb force 2655.22
Watt-hr Horsepower-hr 0.00134102
Watt-hr Joule 3600.0
Watt-hr Kg-force-m 367.098
Watt-sec Erg 10000000.0
Watt-sec Joule 1.0
Watt-sec Newton-m 1.0

16. Chapter 10/Electrical Measurement 275
Inductance Measurement
The most direct method of calcu-lating
inductances is based on the
definition of flux linkages per
ampere. To calculate flux link-ages,
it is necessary to write the
expression for the magnetic
induction at any point of the field,
and then to integrate this expres-sion
over the space occupied by
the flux that is linked to the ele-ment
in question.
Biot-Savart Law of Magnetic
Field Intensity
dH
i ds
r
= 2 sinθ
where
dH = magnetic field density
i = current
ds = length of circuit element
r = radius vector
θ = angle between ds and the
radius vector
Mutual Inductance of Two
Conductors
Values of loge in the equation:
loge R = loge p + loge k
(Longer sides of rectangles in
same straight line.)
γ =
c
1
= p
Δ
B
c
,
See Tables on next page for val-ues.
d
ds
χ
θ
r
c c
B B
p

17. 276 ISA Handbook of Measurement Equations and Tables
Geometric Mean Distances
In calculating the mutual inductance of two conductors whose cross
sectional dimensions are small compared with their distance apart, we
assume that the mutual inductance is the same as the mutual induc-tance
of the filaments along their axes, and use the appropriate basic
formula for filaments to calculate mutual inductance. For conductors
whose cross section is too large to justify this assumption, it is neces-sary
to average the mutual inductances of all the filaments of which the
conductors consist. That is, the basic formula for the mutual inductance
is to be integrated over the cross sections of the conductors.
Values of logc k in equation:
Geometric Mean Distance of Equal Parallel Rectangles,
Longer Sides of Rectangle in Same Straight Line
γ 1 = 0
Δ
.02 .04 .06 .08 1.0
0.05 -0.0002 -0.0002 -0.0002 -0.0001 -0.0001 +0.0000
0.10 -0.0008 -0.0008 -0.0007 -0.0005 -0.0003 +0.0000
0.15 -0.0019 -0.0018 -0.0016 -0.0012 -0.0006 +0.0000
0.20 -0.0034 -0.0032 -0.0028 -0.0021 -0.0012 +0.0000
0.25 -0.0053 -0.0051 -0.0044 -0.0034 -0.0019 +0.0000
0.30 -0.0076 -0.0073 -0.0064 -0.0048 -0.0027 +0.0001
0.35 -0.0105 -0.0100 -0.0087 -0.0066 -0.0036 +0.0002
0.40 -0.0138 -0.0132 -0.0115 -0.0086 -0.0047 +0.0002
0.45 -0.0176 -0.0169 -0.0146 -0.0110 -0.0059 +0.0003
0.50 -0.0220 -0.0210 -0.0182 -0.0136 -0.0073 +0.0005
0.55 -0.0269 -0.0257 -0.0222 -0.0164 -0.0087 +0.0007
0.60 -0.0325 -0.0310 -0.0267 -0.0196 -0.0103 +0.0010
0.65 -0.0388 -0.0369 -0.0316 -0.0231 -0.0120 +0.0014
0.70 -0.0458 -0.0435 -0.0370 -0.0269 -0.0137 +0.0019
0.75 -0.0536 -0.0509 -0.0431 -0.0310 -0.0156 +0.0023
0.80 -0.0625 -0.0591 -0.0470 -0.0354 -0.0176 +0.0031
0.85 -0.0725 -0.0683 -0.0569 -0.0401 -0.0195 +0.0037
0.90 -0.0839 -0.0786 -0.0648 -0.0451 -0.0216 +0.00046
0.95 -0.0973 -0.0903 -0.0734 -0.0504 -0.0236 +0.0056
1.00 -0.1137 -0.1037 -0.0828 -0.0561 -0.0258 +0.0065

18. loge R = logc p + logc k
Chapter 10/Electrical Measurement 277
(Longer sides of the rectangle per-pendicular
to lines joining their
centers.)
B
B
p
c
B
= ,Δ =
Geometric Mean Distances of
Equal Parallel Rectangles (con-cluded)
c c
p
B
Geometric Mean Distance of Equal Parallel Rectangles,
Longer Sides of the Rectangle Perpendicular to Centers
B Δ = 0 0.2 0.4 0.6 0.8 1.0
0.1 0.0008 0.0008 0.0007 0.0005 0.0003 0.0000
0.2 0.0033 0.0032 0.0028 0.0021 0.0012 0.0000
0.3 0.0074 0.0071 0.0062 0.0048 0.0027 0.0001
0.4 0.0129 0.0124 0.0109 0.0084 0.0050 0.0003
0.5 0.0199 0.0191 0.0169 0.0131 0.0077 0.0005
0.6 0.0281 0.0271 0.0240 0.0185 0.0111 0.0011
0.7 0.0374 0.0361 0.0320 0.0251 0.0155 0.0019
0.8 0.0477 0.0461 0.0411 0.0321 0.0200 0.0031
0.9 0.0589 0.0569 0.0506 0.0404 0.0254 0.0046
1.0 0.0708 0.0685 0.0614 0.0492 0.0313 0.0065
0.9 0.0847 0.0821 0.0738 0.0596 0.0382
0.8 0.1031 0.0999 0.0903 0.0745 0.0485
0.7 0.1277 0.1240 0.1125 0.0925
0.6 0.1618 0.1573 0.1436 0.1194
0.5 0.2107 0.2053 0.1886
0.4 0.2843 0.2776 0.2567
0.3 0.4024 0.3942
0.2 0.6132 0.6021
0.1 1.0787

19. 278 ISA Handbook of Measurement Equations and Tables
For accurate interpolation in the case of broad rectangles, near together
(1/B small and D small), write:
loge R = loge B + loge K'
Values for logeK'
1/B Δ = 0 0.1 0.2 0.3 0.4 0.5
0.00 -1.5000
0.05 -1.3542
0.10 -1.2239 -1.2278
0.15 -1.1052 -1.1084
0.20 -0.9962 -0.9989 -1.0073
0.25 -0.8953 -0.8977 -0.9049
0.30 -0.8015 -0.8037 -0.8098 -0.8208
0.35 -0.7140 -0.7159 -0.7215 -0.7311
0.40 -0.6321 -0.6337 -0.6387 -0.6472 -0.6596
0.45 -0.5550 -0.5565 -0.5610 -0.5687 -0.5797
0.50 -0.4825 -0.4838 -0.4879 -0.4948 -0.5046 -0.5178

20. Chapter 10/Electrical Measurement 279
Values of Constants for the Geometric Mean Distance of a Rectangle
Sides of the rectangle are B and c. The geometric mean distance R is
given by:
loge R = loge (B + c) - 1.5 + loge e.
R = K (B + c), loge K = - 1.5 + loge e
Geometric Mean Distance of a Line of Length (a) from Itself
loge R = loge a − 3
or
Circular Area of Radius (a) from Itself
loge R = loge a − 1
or
Ellipse with Semiaxes (a) and (b)
a +
b loge R =
loge
−
2
1
4
R = 0.7788a
4
R = 0.22313a
2
Values for Constants K, logee
B/c or c/B K loge e B/c or c/B K loge e
0.00 0.22313 0.0000 0.50 0.22360 0.00211
0.025 0.22333 0.00089 0.55 0.22358 0.00203
0.05 0.22346 0.00146 0.60 0.22357 0.00197
0.10 0.22360 0.00210 0.65 0.22356 0.00192
0.15 0.22366 0.00239 0.70 0.22355 0.00187
0.20 0.22369 0.00249 0.75 0.22354 0.00184
0.25 0.22369 0.00249 0.80 0.22353 0.00181
0.30 0.22368 0.00244 0.85 0.22353 0.00179
0.35 0.22366 0.00236 0.90 0.22353 0.00178
0.40 0.22364 0.00228 0.95 0.223525 0.00177
0.45 0.22362 0.00219 1.00 0.223525 0.00177

21. 280 ISA Handbook of Measurement Equations and Tables
Geometric Mean Distance of an
Annulus from Itself
Geometric Mean Distance of a
Point or Area from an Annulus
log
2
2
p log p p log
p
e
R e e
2
p p
=
−
−
1 1 2
2
−
1
2
2
1
2
loge R = logp1− logeζ
point
A area
p1
p2
Values for Geometric Mean Distance of an Annulus
p2/p1 logeζ d1 d2
0.00 0.2500 -12
0.05 0.2488 -36 -24
0.10 0.2452 -57 -21
0.15 0.2395 -75 -18
0.20 0.2320 -92 -16
0.25 0.2228 -105 -14
0.30 0.2123 -116 -12
0.35 0.2007 -127 -10
0.40 0.1880 -135 -8
0.45 0.1745 -142 -7
0.50 0.1603 -144 -6
0.55 0.1456 -147 -5
0.60 0.1304 -152 -4
0.65 0.1148 -156 -3
0.70 0.0989 -159 -3
0.75 0.0827 -162 -2
0.80 0.0663 -163 -1
0.85 0.0499 -164 -1
0.90 0.0333 -165 -1
0.95 0.0167 -166 -1
1.00 0.0000 -167

22. Chapter 10/Electrical Measurement 281
Inductance of Parallel Elements of Equal Length
Mutual Inductance of Two Equal Parallel Straight Filaments
or
2
2 . log
M l
M = 0.002lQ
l
d
2
2
l
d
d
l
d

e l = + +
 

 
− + +






0 002 1 1
Values for Q, d/l
ι
p
d/l Q d1
0.050 2.7382 -903
0.055 2.6479 -822
0.060 2.5657 -752
0.065 2.4905 -693
0.070 2.4212 -642
0.075 2.3570 -597
0.080 2.2973 -558
0.085 2.2415 -524
0.090 2.2189 -493
0.095 2.1398 -466
0.100 2.0932 -440
0.105 2.0492 -418
0.110 2.0074 -397
0.115 1.9677 -379
0.120 1.9298 -361
0.125 1.9837 -345
0.130 1.8592 -330
0.135 1.8262 -318
0.140 1.7944 -305
0.145 1.7639 -293
0.150 1.7346 -281

23. 282 ISA Handbook of Measurement Equations and Tables
Values for Q, d/l (cont.)
d/l Q d1
0.155 1.7065 -271
0.160 1.6794 -262
0.165 1.6532 -253
0.170 1.6279 -244
0.175 1.6035 -236
0.180 1.5799 -228
0.185 1.5571 -222
0.190 1.5349 -215
0.195 1.5134 -208
0.200 1.4926 -398
0.210 1.4528 -376
0.220 1.4152 -355
0.230 1.3797 -337
0.240 1.3460 -321
0.250 1.3139 -305

24. Chapter 10/Electrical Measurement 283
Values for Q, d/l (cont.)
d/l Q d1 d/l Q d1
0.260 1.2834 -290 0.520 0.8016 -227
0.270 1.2544 -277 0.540 0.7789 -215
0.280 1.2267 -265 0.560 0.7574 -204
0.290 1.2002 -253 0.580 0.7370 -194
0.300 1.1749 -243 0.600 0.7176 -184
0.310 1.1506 -233 0.620 0.6992 -175
0.320 1.1273 -224 0.640 0.6817 -167
0.330 1.1049 -214 0.660 0.6650 -160
0.340 1.0835 -207 0.680 0.6490 -152
0.350 1.0627 -199 0.700 0.6338 -145
0.360 1.0429 -192 0.720 0.6193 -139
0.370 1.0238 -186 0.740 0.6054 -134
0.380 1.0052 -178 0.760 0.5920 -128
0.390 0.9874 -172 0.780 0.5792 -122
0.400 0.9702 -166 0.800 0.5670 -118
0.410 0.9536 -161 0.820 0.5552 -113
0.420 0.9375 -156 0.840 0.5439 -109
0.430 0.9219 -151 0.860 0.5330 -105
0.440 0.9068 -146 0.880 0.5225 -101
0.450 0.8922 -141 0.900 0.5124 -97
0.460 0.8781 -137 0.920 0.5027 -93
0.470 0.8644 -133 0.940 0.4934 -90
0.480 0.8511 -130 0.960 0.4843 -87
0.490 0.8381 -125 0.980 0.4756 -84
0.500 0.8256 -240 1.000 0.4672 -81

25. 284 ISA Handbook of Measurement Equations and Tables
Values for Q, l/d
l/d Q d1 l/d Q d1
1.00 0.4672 -84 0.50 0.2451 -94
0.98 0.4588 -83 0.48 0.2357 -95
0.96 0.4505 -84 0.46 0.2262 -96
0.94 0.4421 -85 0.44 0.2166 -95
0.92 0.4336 -85 0.42 0.2071 -96
0.90 0.4251 -85 0.40 0.1975 -97
0.88 0.4166 -86 0.38 0.1878 -97
0.86 0.4080 -87 0.36 0.1781 -97
0.84 0.3993 -87 0.34 0.1684 -97
0.82 0.3906 -87 0.32 0.1587 -98
0.80 0.3819 -88 0.30 0.1489 -98
0.78 0.3731 -88 0.28 0.1391 -98
0.76 0.3643 -89 0.26 0.1293 -99
0.74 0.3554 -90 0.24 0.1194 -98
0.72 0.3464 -90 0.22 0.1096 -99
0.70 0.3374 -90 0.20 0.0977 -99
0.68 0.3284 -91 0.18 0.0898 -100
0.66 0.3193 -91 0.16 0.0798 -99
0.64 0.3102 -92 0.14 0.0699 -100
0.62 0.3011 -93 0.12 0.0599 -99
0.60 0.2918 -92 0.10 0.0500 -100
0.58 0.2826 -93 0.08 0.0400 -100
0.56 0.2733 -93 0.06 0.0300 -100
0.54 0.2640 -94 0.04 0.0200 -100
0.52 0.2546 -95 0.02 0.0100 -100

26. Mutual Inductance of Two Equal
Parallel Conductors
2
2 . log log
d
l = e − e − + −
M l
l
d
k
Self-Inductance of a Straight
Conductor
General Formula
L l
ζ
where
r = geometric mean distance
ζ1= arithmetic mean distance of
the points of the cross section
For a Round Wire, Radius p
e p =  −
For a Round Magnetic Wire
e p =  − +
where
μ = permeability
For Rectangular Wire, Sides B
and C
 + −
= . log e log
e e
+
where
B and C = see table, Values of
constants for Geometric Mean
Distance for Rectangles
For Elliptical Wire
L l
where
α = β semiaxes of the ellipse
Inductance of Multiple
Conductors
Two Equal Parallel Wires, Sepa-rated
by Distance (d) between
Centers
l
pd = e −
Three Equal Parallel Wires, at the
Corners of an Equilateral Triangle
of Side (d)
L l

where
r = geometric mean distance of
circular area of radius (p)
Inductance of a Return Circuit of
Parallel Conductors
Equal Round Wires of Radius (p)
e l =  + −
Equal Permeable Round Wires
L l
=  d
e + −
p
l d
 

 
0 004
4
. log
μ
L l
d
p
d
 

 
0 004
1
4
. log
l
rd = e −
 

 
0 002
2
1 2 1 3 . log
( )/
L l

 

 
0 002
2 7
8
. log
l
= e
+
−

 

 
0 002
2
. log 0.05685
α β
L l
l
B C
 

 
0 002
2 1
2
L l
l
 

 
0 002
2
1
4
. log
μ
L l
l
 

 
0 002
2 3
4
. log
l
e r l =  − +
 

 
0 002
2
. log 1 1
d
l

 

 
0 002
2
1
1
4
Chapter 10/Electrical Measurement 285

27. 286 ISA Handbook of Measurement Equations and Tables
Return Circuit of Two Tubular Conductors, One Inside the Other


0 002 ×
2 . log loge loge loge
where
loge ζ1 and loge ζ3 = values from table, geometric mean distance of
an annulus
Return Circuit of Polycore Cable
L l
p
a
P
P
p
p

 

 

Mutual Inductance of Unequal Parallel Filaments
General Formula
=  − d
0.001 αsin −1 sin −1 − sin −1 + sin −1 − 2 + 2
M h
where
α = l + m − ζ
β = l − ζ
γ = m − ζ
d
h
d
h
d
h
d
 

 
α
β
β
γ
γ
ζ
ζ
 α
 

 
+ + + + − + 

β2 d2 γ 2 d2 ζ2 d2
p
e e p = +
−

 

 




0 002
2
1
1
2
1
2
2
1
2
1
2
. log log

+  + + −
 

 
1 1
4
1
n
a
e n e n log ρ log ξ
L l
p
p
P
P
p
p
= e +

 

 
−

 

 




2
1
1
3
2
1
2
2
1
p
p
1
2
−1+ 1 + 3

 

 
ζ ζ
p
a
p1
p2
ι
ζ m
p

28. Mutual Inductance of Filaments Inclined at an Angle
Equal Filaments Meeting at a
Point
2 = 2 2(1− cos ε)
R1 l
Mutual Inductance between
Filaments
or
M l h
M = 0.001lS
l
l R
=
+
0 004 −1
1
. cos ε tan
ι
ε
Value of Factor S (cont.)
cos ε S d1
-0.05 -0.0867 -867
-0.10 -0.1707 -840
-0.15 -0.2523 -815
-0.20 -0.3316 -793
-0.25 -0.4088 -772
-0.30 -0.4840 -752
-0.35 -0.5574 -734
-0.40 -0.6290 -716
-0.45 -0.6991 -701
-0.50 -0.7677 -686
-0.55 -0.8348 -671
-0.60 -0.9006 -658
-0.65 -0.9651 -645
-0.70 -1.0284 -633
-0.75 -1.0906 -622
-0.80 -1.1517 -611
-0.85 -1.2118 -601
-0.90 -1.2709 -591
-0.95 -1.3290 -581
-1.00 -1.3862 -572
Values of Factor S
cos ε S d1
0.95 3.7830 -7236
0.90 3.0594 -4462
0.85 2.6132 -3316
0.80 2.2816 -2679
0.75 2.0137 -2274
0.70 1.7863 -1991
0.65 1.5872 -1780
0.60 1.4092 -1618
0.55 1.2474 -1488
0.50 1.0986 -1382
0.45 0.9604 -1294
0.40 0.8310 -1218
0.35 0.7092 -1154
0.30 0.5938 -1097
0.25 0.4841 -1048
0.20 0.3793 -1003
0.15 0.2789 -964
0.10 0.1825 -929
0.05 0.0896 -896
0.00 0.0000 -867
Chapter 10/Electrical Measurement 287
ι
R1

29. 288 ISA Handbook of Measurement Equations and Tables
Unequal Filaments Meeting at a Point
M l h
or M = 0.001l1 S1
m
l R
m h
l
m R
=
+

 

 
+ −
+

 

 
0 002 − 1 1
1 1
1
1
1
1
. cos ε tan tan
Values for S1, Unequal Filaments Meeting at a Point
cos ε m
1
1
l
= 1 0.8 0.6 0.4 0.2
0.95 3.7830 3.3406 2.7622 2.0473 1.1776
0.90 2.0594 2.7095 2.2597 1.6957 0.9918
0.85 2.6132 2.3178 1.9422 1.4690 0.8688
0.80 2.2816 2.0256 1.7028 1.2950 0.7727
0.75 2.0137 1.7889 1.5073 1.1513 0.6917
0.70 1.7863 1.5876 1.3402 1.0272 0.6209
0.65 1.5872 1.4113 1.1931 0.9172 0.5572
0.60 1.4092 1.2534 1.0609 0.8177 0.4991
0.55 1.2474 1.1098 0.9404 0.7264 0.4452
0.50 1.0986 0.9776 0.8291 0.6417 0.3947
0.40 0.8310 0.7398 0.6283 0.4880 0.3020
0.30 0.5938 0.5288 0.4496 0.3501 0.2179
0.20 0.3793 0.3378 0.2876 0.2244 0.1404
0.10 0.1825 0.1626 0.1385 0.1083 0.0680
0.00 0.0000 0.0000 0.0000 0.0000 0.0000
-0.10 -0.1707 -0.1522 -0.1298 -0.1018 -0.0644
-0.20 -0.3316 -0.2956 -0.2523 -0.1982 -0.1257
-0.30 -0.4840 -0.4314 -0.3684 -0.2898 -0.1844
-0.40 -0.6290 -0.5608 -0.4791 -0.3772 -0.2406
-0.50 -0.7677 -0.6845 -0.5850 -0.4611 -0.2948
-0.60 -0.9006 -0.8031 -0.6865 -0.5416 -0.3470
-0.70 -1.0284 -0.9172 -0.7844 -0.6194 -0.3976
-0.80 -1.1517 -1.0272 -0.8788 -0.6944 -0.4467

30. Unequal Filaments in the Same
Plane, Not Meeting
Equations Connecting the Two
Systems
where
= R −R +R −R2
2
2 2 2
2
2 2
2
2
2
l m R R l R R m
( ) ( )
2
2
( ) α (
2 2 2
2
= + + + − + +
= + + − +
2 2
μ μ ε
μ μ ε
R l vm lvm
R l v v l
( ) ( ) ( )( )cos
( ) ( )cos
2 2 2
2 2 2
= + −
= + + − +
μ μ ε
μ μ ε
2 2 2
cos
( ) ( )cos
Equation for Mutual Inductance
M
l h
m
R R
ε

= μ
+
 
+ +
v m h
l
R R
h
m
R
2
1
+
1 2
1
1 4
1
cos
( )tan
μ

 
( )tan tan
+
−
−
− −
3 4
1
2 3
+

 

 
−
+

 

 
−
R
v h
l
R R
tan
1
2
2
2
R 3
v v
R v m v m
4
2
2
v
m l R R m R R l
l m
=
− − + − − 

−
2
4
2
4
3
2
2
2
3
2 2 4
α
μ
α
α
=
− − + − − 

−
l m
2
4
2
2
3
4
3
2 2 4
α2
4
3
2
1
2
2
cos ε
α
=
lm
Chapter 10/Electrical Measurement 289
b m
C
a
A B
d
p
p
ν
ε
ι
ν
μ
ι
R3
R4
R1
R2
∈
m

31. 290 ISA Handbook of Measurement Equations and Tables
Mutual Inductance of Two Filaments
Placed in Any Desired Position
where
tan
ε
= μ
+
μ
d lv m
 +
− 
ε μ ε
d v m
Circuits Composed of Combinations of Straight Wires
Equation for the Inductance of a Triangle of Round Wire


− + − 0 002
L a
 + −
− − + − ( )sin h ( )sin
where
2 a
2 2 1
b
b
V 2 = 2(a2b2 + a2c2 + b2c2) − a4 −b4 − c4
a,b,c = sides of the triangle
c
c
b c h
c b a
= e + e + e
 

 
− −
2 2
. log log log ( )sin
ρ ρ ρ
2
1
2
2
2
1
2 2
V
a b
a b c
V
a c h
 
a c

 
− +
 

 − +
b
V
a b c
a b c
2
4
− + +

 

 
+  + +
 

 
( )
( )
μ
ω
ε μ ε
ε
ε
=
 + + +
 

 
−
+
−
−
cos ( )( )sin
sin
tan
cos (
1
2 2
1
1
2
dR
d μμ ε
ε
ε μ ε
ε
 

 
=
 +
 
l v
dR
d v
dR
) sin
sin
tan
cos sin
sin
2
2
1
2 2
3  
−
 + +
 

 
tan−
cos ( )sin
sin
1
2 2
4
dR
ε
M
l h
m
R R
v m h
l
R R
0 001
2
2
1
1 2
1
1 4
. cos
( )tan
( )tan ta
+

 

 
+ +
+
−
−
− n
tan
sin
h
m
R R
v h
R R
d
−
−
+

 

 
−
+

 

 
−
Ω
1
3 4
1
2 3
2
1
ε

32. Equation for the Inductance of a Rectangle of Round Wire

2 2
μ
(a b) (a b)
Regular Polygons of Round Wire
Equilateral Triangle
Square
Pentagon
Hexagon
Octagon





= e + +
L s
s
 
Equation for the Calculation of Inductance of Any Plane Figure

2
α
= 0 002
e − +
. logρ
L l
l
 

 
μ
4
where
l = perimeter of the figure

 
0 016 0 21198
4
. log .
ρ
μ
L s
s
= e − +
 

 
0 012 0 15152
4
. log .
ρ
μ
L s
s
= e − +
 

 
0 010 0 40914
4
. log .
ρ
μ
L s
s
= e − +
 

 
0 008 0 77401
4
. log .
ρ
μ
L s
s
= e − +
 

 
0 006 1 40546
4
. log .
ρ
μ
L a
a b
a b a h
a
b
b h
b
e e a = + + +
 

 
−  −

0 004 − −
. log log 2 2 2 sin 1 sin 1
ρ ρ 

 
−  + + +
 

 
2
4
Chapter 10/Electrical Measurement 291

33. 292 ISA Handbook of Measurement Equations and Tables
Values for α (alpha) for Certain Plane Figures
Rectangles
β α
0.05 4.494
0.10 3.905
0.15 3.589
0.20 3.404
0.25 3.270
0.30 3.172
0.40 3.041
0.50 2.962
0.60 2.913
0.70 2.882
0.80 2.865
0.90 2.856
1.00 2.854
Isosceles Triangles
ε α
5° 4.884
10° 4.152
20° 3.690
30° 3.424
40° 3.284
50° 3.217
60° 3.197
70° 3.214
80° 3.260
90° 3.331
100° 3.426
110° 3.546
120° 3.696
130° 3.875
140° 4.105
150° 4.399
160° 4.813
170° 7.514

34. Chapter 10/Electrical Measurement 293
Mutual Inductance of Equal,
Parallel, Coaxial Polygons of
Wire
s = length of the side of the
polygon.
d = distance between their
planes.
Squares
2a 4
d
= ∫F 4
2π
Equilateral Triangles
2a 3
d
= ∫F 3
2π
Hexagons
2a 6
d
M
= 6
s
∫F 2π
s
d
=    
π
M
s
s
d
=  
 
π
M
s
s
d
=  
 
π
Regular Polygons
N α
3 3.197
4 2.854
5 2.712
6 2.636
7 2.591
8 2.561
9 2.542
10 2.529
11 2.519
12 2.513
13 2.506
14 2.500
15 2.495
16 2.492
17 2.489
18 2.486
19 2.484
20 2.482
21 2.481
22 2.480
23 2.478
24 2.477
∞ 2.452

35. 294 ISA Handbook of Measurement Equations and Tables
Values for (F) in Coaxial Equal Polygons, d/s
d/s Triangles F Diff. Squares F Diff. Hexagon F Diff.
0.00 1.0000 1.000 1.000
0.05 0.7245 -2755 0.8642 -1358 0.9449 -551
0.10 0.6640 -605 0.8362 -280 0.9350 -99
0.15 0.6217 -423 0.8165 -197 0.9283 -67
0.20 0.5890 -327 0.8007 -158 0.9231 -52
0.25 0.5624 -266 0.7875 -132 0.9188 -43
0.30 0.5402 -222 0.7760 -115 0.9150 -38
0.35 0.5215 -187 0.7658 -102 0.9117 -33
0.40 0.5054 -161 0.7565 -93 0.9087 -30
0.45 0.4914 -140 0.7480 -85 0.9057 -30
0.50 0.4792 -122 0.7402 -78 0.9029 -28
0.55 0.4686 -106 0.7329 -73 0.9003 -26
0.60 0.4592 -94 0.7262 -67 0.8078 -25
0.65 0.4507 -85 0.7200 -62 0.8054 -24
0.70 0.4437 -70 0.7140 -60 0.8031 -23
0.75 0.4372 -65 0.7085 -55 0.8906 -25
0.80 0.4314 -58 0.7035 -50 0.8884 -22
0.85 0.4263 -51 0.6988 -47 0.8863 -21
0.90 0.4216 -47 0.6941 -47 0.8843 -20
0.95 0.4175 -41 0.6899 -42 0.8823 -20
1.00 0.4138 -37 0.6861 -38 0.8802 -21

36. Chapter 10/Electrical Measurement 295
Values for (F) in Coaxial Equal Polygons, s/d
s/d Triangles F Diff. Squares F Diff. Hexagon F Diff.
1.00 0.4138 0.6861 0.8802
0.90 0.4066 -72 0.6783 -78 0.8761 -41
0.80 0.3996 -70 0.6701 -82 0.8713 -48
0.70 0.3930 -66 0.6613 -88 0.8656 -57
0.60 0.3866 -64 0.6525 -88 0.8592 -64
0.50 0.3808 -58 0.6439 -86 0.8518 -74
0.40 0.3757 -51 0.6362 -77 0.8440 -78
0.30 0.3714 -43 0.6289 -73 0.8364 -76
0.20 0.3682 -32 0.6221 -68 0.8297 -67
0.10 0.3662 -20 0.6182 -39 0.8243 -54
0.00 0.3655 -7 0.6169 -13 0.8225 -18
Coaxial Triangles

4
4 . log . . ....
d
s = e − + − +
M s
 
Coaxial Squares
s
d
d
s
d
s
2
4
. log . . . ....
2
4 d
s = e − + − −
Coaxial Hexagons

2
4
. log . . . . .... 2
4 d
s = e − + + −
M s
s
d
d
s
d
s


0 012 0 15152 0 3954 0 1160 0 052

 
M s
s
d
d
s
d
s

 

 
0 008 0 7740 0 0429 0 109

0 006 1 4055 2 209
11
12
203
864
2
2
 

37. Inductance of Single-Layer Coils on Rectangular Winding Forms

2
2 . sin sin
L N

2 1
1
− 1
3
where
g2 a2 a
= + 2
1
aa
b
1
2
b
a
h
a
b
1
2
b
a
h
a
b
a
b
b
a

= + − −
 

 
0 008 − −
1
2
2 1 1
1
1 11 1
1
1
2
2
1
1 1
1
1
1
1
2
1
2
sin
sin sin
h
a
b
a
b
a
b
h
a
a
a
b
h
a
−
− −
+





aa

− − 1 1 1
2
2
2
2
1
2
2
2

2 2
1
1
3
1 1
1
a 2
b
g
b
b
aa
g
b
g
b
+ −
+




+ +


π −
tan 

 






+ − + −
 

 
1
3
1 1
1
2
2
1
2
2
2
2
b
aa
b
aa
a
b
a
b
b2
1
2
2
a
b
1
2
2
a
b
1
b
aa
1
3 3
3
1
1

3 2
2
1
1
2
1
aa 6
g a a
b
− −
 

 
+

 

 







296 ISA Handbook of Measurement Equations and Tables

38. Coefficients, Short Rectangle Solenoid
 ′ = 1

+ 1 1
β
1 π
 
k
Chapter 10/Electrical Measurement 297
κ β1
’ β1 β2 β3 β5 β7
1.00 0.4622 0.6366 0.2122 -0.0046 0.0046 -0.0382
0.95 0.4574 0.6534 0.2234 -0.0046 0.0053
0.90 0.4512 0.6720 0.2358 -0.0046 0.0064 -0.0525
0.85 0.4448 0.6928 0.2496 -0.0042 0.0080
0.80 0.4364 0.7162 0.2653 -0.0031 0.0103 -0.0838
0.75 0.4260 0.7427 0.2829 -0.0010 0.0141
0.70 0.4132 0.7730 0.3032 0.0026 0.0198 -0.1564
0.65 0.3971 0.8080 0.3265 0.0085 0.0291
0.60 0.3767 0.8488 0.3537 0.0179 0.0432 -0.3372
0.55 0.3500 0.8970 0.3858 0.0331 0.0711
0.50 0.3151 0.9549 0.4244 0.0578 0.1183 -0.7855
0.40 0.1836 1.1141 0.5305 0.1679 0.3898 -2.4030
0.30 -0.0314 1.3359 0.7074 0.5433 2.0517 -7.850
0.20 -0.6409 1.9099 1.0610 2.3230 14.5070 15.51
0.10 -3.2309 3.5014 2.1220 22.5480 497.360 14282.0

39. 298 ISA Handbook of Measurement Equations and Tables
Self-Inductance of Circular
Coils of Rectangular Cross-
Section
Nomenclature
a = mean radius of turns
b = axial dimension of the
cross-section
c = radial dimension of the
cross-section
N = total number of turns
nb = number of turns per layer
nc = number of layers
pb = distance between centers
of adjacent turns in the
layer
pc = distance between centers
of corresponding wires in
consecutive layers
=
=
=
b n p
c np
N nn
b b
c c
b c
For Closely Wound Coils:
=
=
=
δ
δ
b n
c n
N
b
c
bc
δ
where
pb = pc
δ = diameter of the covered wire
c
b
a