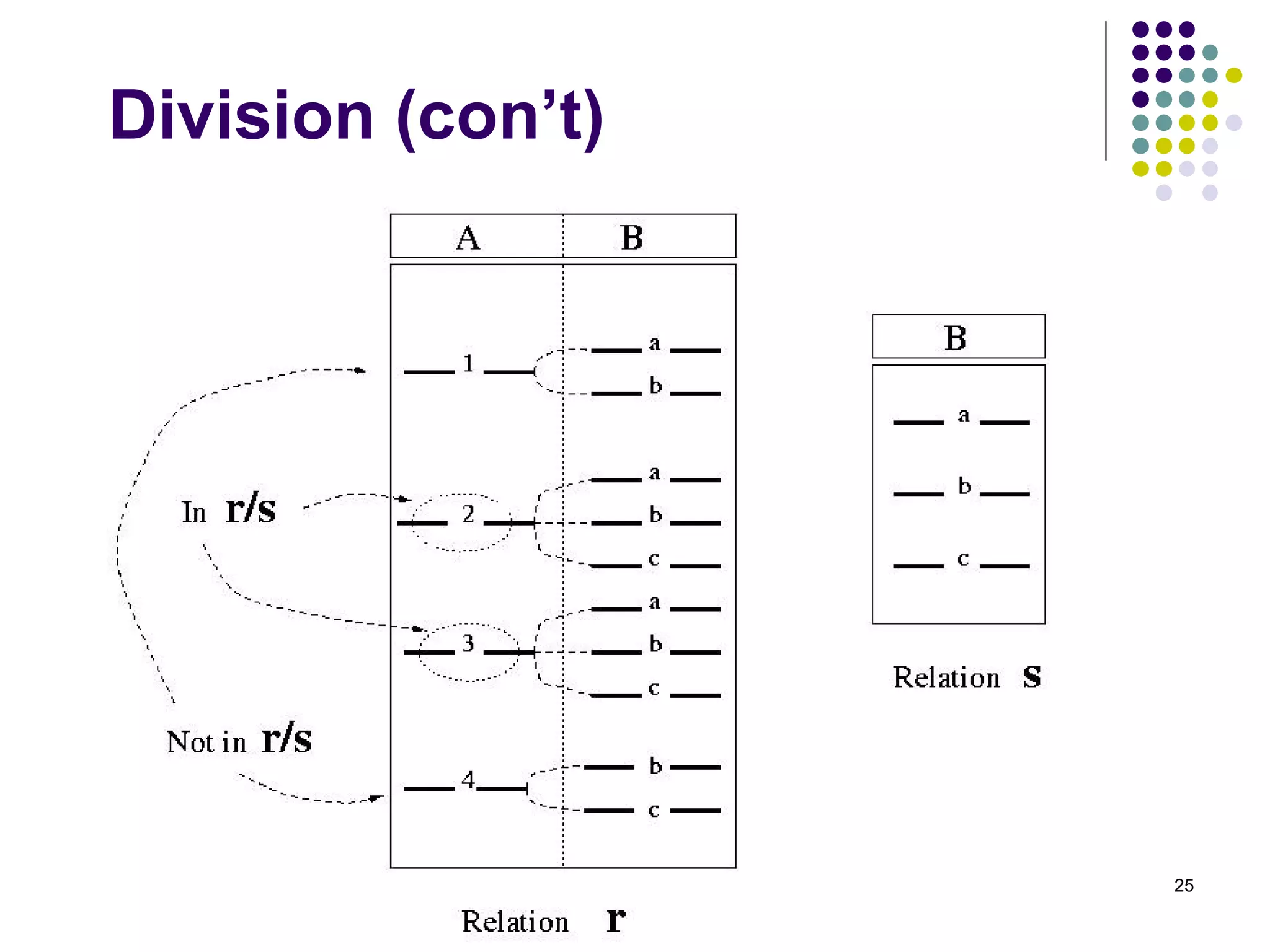
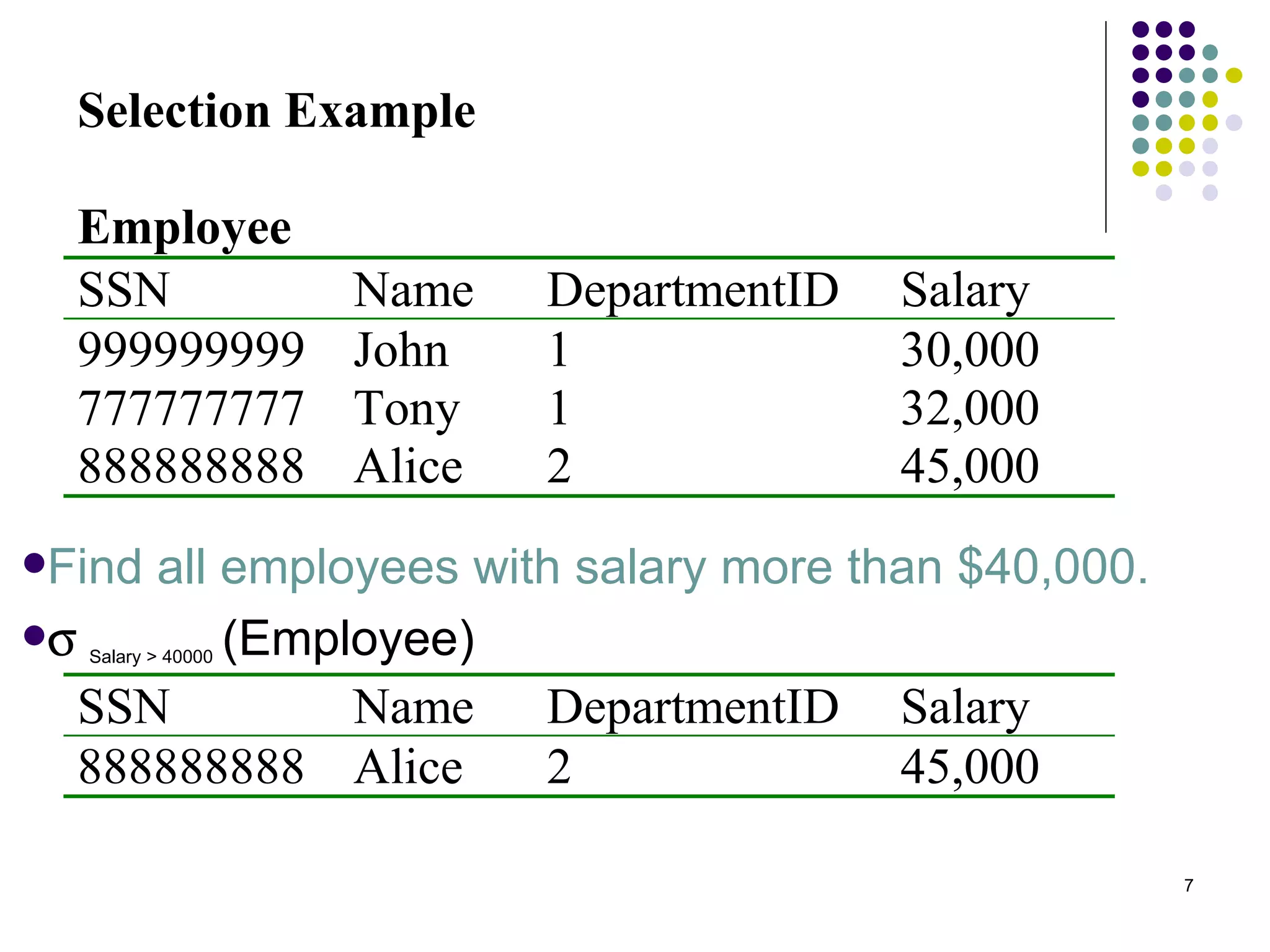
The document discusses relational algebra operations including selection, projection, join, union, intersection, difference, and cartesian product. It provides examples of how to write queries using these operations, such as selecting tuples that satisfy certain conditions, extracting certain attributes, combining relations, and performing joins between relations. Key operations like selection, projection, equijoin and natural join are explained in detail with examples.

1. Database Systems: Chapter 6: Relational Algebra Dr. Taysir Hassan Abdel Hamid Lecturer, IS Department Faculty of Computer and Information Assiut University Contact: [email_address] March 30, 2008

2. Operations in Relational Algebra Group one : includes set operations from mathematical set theory: UNION, INTERSECTION, SET DIFFERENCE, AND CARTESIAN PRODUCT. Group two : includes operations specifically for relational databases: SELECT, PROJECT, AND JOIN Common database requests cannot be performed with the original relational operations.

3. Unary Relational Operations SELECT SELECT operation is used to select a subset of the tuples from a relation that satisfies a selection condition. One can consider the SELECT operation to be a filter that keeps only those tuples that satisfy a qualifying condition. SELECT can also be visualized as a horizontal partition of the relation into two sets of tuples.

4. Select Operator Produce table containing subset of rows of argument table satisfying condition Example: 1123 John 123 Main stamps 1123 John 123 Main coins 5556 Mary 7 Lake Dr hiking 9876 Bart 5 Pine St stamps 1123 John 123 Main stamps 9876 Bart 5 Pine St stamps Person Id Name Address Hobby Id Name Address Hobby

5. Selection Condition Operators: <,  ,  , >, =,  Simple selection condition: <attribute> operator <constant> <attribute> operator <attribute> <condition> AND <condition> <condition> OR <condition> NOT <condition> NOTE: Each attribute in condition must be one of the attributes of the relation name

6.  Id>3000 OR Hobby=‘hiking’ (Person)  Id>3000 AND Id <3999 (Person)  NOT(Hobby=‘hiking’) (Person)  Hobby  ‘hiking’ (Person)  (Id > 3000 AND Id < 3999) OR Hobby  ‘hiking’ (Person) Selection Condition - Examples

7. Find all employees with salary more than $40,000.  Salary > 40000 (Employee)

8. Projection Extracts some of the columns from a relation. SexSalary :=  (EMPLOYEE, (SEX, SALARY)) No attribute may occur more than once. Duplicate will be removed. Projection and selection combined.  (  (EMPLOYEE, CITY = “LONDON”), (NAME,SSN)) This does a selection followed by a projection. The DBMS may re-organise this for faster retrieval.

9. Union Produce a relation which combines two relations by containing all of the tuples from each - removing duplicates. The two relations must be &quot; union compatible &quot; i.e. have the same number of attributes drawn from the same domain (but maybe having different names). LondonOrRich: =  EMPLOYEE, CITY = “LONDON”)  (EMPLOYEE, SALARY > 60K) If attribute names differ, the names from the first one are taken. Same can be done using disjuncts!

10. Intersection Similar to union but returns tuples that are in both relations. FemalesInLondon :=  EMPLOYEE, CITY = “LONDON”)  (EMPLOYEE, SEX = “F”) Same can be done with conjuncts!

11. Difference Similar to union but returns tuples that are in the first relation but not the second. NonLocals := EMPLOYEE - LOCALS Intersection and difference both require union compatibility. Intersection and difference use column names from the first relation.

12. Union Compatible Relations Two relations are union compatible if Both have same number of columns Names of attributes are the same in both Attributes with the same name in both relations have the same domain Union compatible relations can be combined using union, intersection, and set difference

13. Example Tables: Person (SSN, Name, Address, Hobby) Professor (Id, Name, Office, Phone) are not union compatible. However

14. Cartesian Product If R and S are two relations, R  S is the set of all concatenated tuples <x,y>, where x is a tuple in R and y is a tuple in S ( R and S need not be union compatible) R  S is expensive to compute: Factor of two in the size of each row Quadratic in the number of rows a b c d a b c d x1 x2 y1 y2 x1 x2 y1 y2 x3 x4 y3 y4 x1 x2 y3 y4 x3 x4 y1 y2 R S x3 x4 y3 y4 R  S

15. Renaming Result of expression evaluation is a relation Attributes of relation must have distinct names. This is not guaranteed with Cartesian product e.g., suppose in previous example a = c Renaming operator tidies this up. To assign the names A 1 , A 2 ,… A n to the attributes of the n column relation produced by expression use expression [A 1 , A 2 , … A n ]

16. Example This is a relation with 4 attributes: StudId, SCrsCode, ProfId, PCrsCode

17. Derived Operation: Join The expression :  join-condition ´ (R  S) where join-condition ´ is a conjunction of terms: A i oper B i in which A i is an attribute of R, B i is an attribute of S, and oper is one of =, <, >,   ,  , is referred to as the (theta) join of R and S and denoted: R join-condition S Where join-condition and join-condition ´ are (roughly) the same …

18. Join and Renaming Problem : R and S might have attributes with the same name – in which case the Cartesian product is not defined Solution : Rename attributes prior to forming the product and use new names in join-condition ´ . Common attribute names are qualified with relation names in the result of the join

19. Theta Join – Example Output the names of all employees that earn more than their managers.  Employee.Name (Employee MngrId=Id AND Salary>Salary Manager) The join yields a table with attributes: Employee.Name, Employee.Id, Employee.Salary, MngrId Manager.Name, Manager.Id, Manager.Salary

20. Equijoin Join - Example  Name,CrsCode ( Student Id=StudId  Grade=‘A’ (Transcript)) Id Name Addr Status 111 John ….. ….. 222 Mary ….. ….. 333 Bill ….. ….. 444 Joe ….. ….. StudId CrsCode Sem Grade 111 CSE305 S00 B 222 CSE306 S99 A 333 CSE304 F99 A Mary CSE306 Bill CSE304 The equijoin is commonly used since it combines related data in different relations. Student Transcript Equijoin: Join condition is a conjunction of equalities .

21. Natural Join Special case of equijoin: join condition equates all and only those attributes with the same name (condition doesn’t have to be explicitly stated) duplicate columns eliminated from the result Transcript (StudId, CrsCode, Sem, Grade) Teaching (ProfId, CrsCode, Sem) Transcript Teaching =  StudId, Transcript.CrsCode, Transcript.Sem, Grade, ProfId ( Transcript CrsCode=CrsCode AND Sem=Sem Teaching) [StudId, CrsCode, Sem, Grade, ProfId ]

22. Natural Join (con’t) More generally: R S =  attr-list (  join-cond (R × S) ) where attr-list = attributes (R)  attributes (S) (duplicates are eliminated) and join-cond has the form: A 1 = A 1 AND … AND A n = A n where {A 1 … A n } = attributes(R)  attributes(S)

23. Natural Join Example List all Id’s of students who took at least two different courses:  StudId (  CrsCode  CrsCode2 ( Transcript Transcript [StudId, CrsCode2, Sem2, Grade2])) (don’t join on CrsCode, Sem, and Grade attributes)

24. Division Goal: Produce the tuples in one relation, r, that match all tuples in another relation, s r (A 1 , …A n , B 1 , …B m ) s (B 1 …B m ) r/s , with attributes A 1 , …A n , is the set of all tuples <a> such that for every tuple <b> in s, <a,b> is in r Can be expressed in terms of projection, set difference, and cross-product

25. Division (con’t)

26. Division - Example List the Ids of students who have passed all courses that were taught in spring 2000 Numerator : StudId and CrsCode for every course passed by every student  StudId, CrsCode (  Grade  ‘F’ (Transcript) ) Denominator : CrsCode of all courses taught in spring 2000  CrsCode (  Semester=‘S2000’ (Teaching) ) Result is numerator/denominator