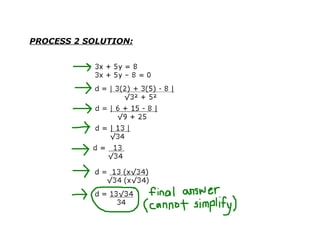
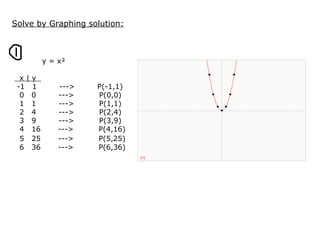
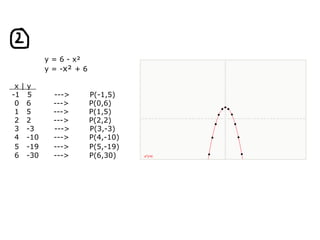
This document provides examples and solutions for solving various types of coordinate geometry problems. It covers changing coordinate equations into standard form, writing equations given a center and radius, finding perpendicular distance between points and lines, and solving systems of linear equations graphically and algebraically. Methods demonstrated include substitution, elimination, and graphing lines to find their point of intersection.

2. COORDINATE EQUATION PROBLEMS: PROCESS 1 EXAMPLES: a) Given the coordinate equation 7 = (x-5)² + (y+6)², change it to the form 0 = x² + y² + dx + ey + f . b) Given the coordinate equation 18 = (x+3)² + (y-4)², change it to the form 0 = x² + y² + dx + ey + f .

3. Solution to a) : Solution to b): PROCESS 1 SOLUTIONS:

4. PROCESS 2 EXAMPLES: c) Given the centre (-4,7), and the radius √26, write the coordinate equation. d) Given the centre (9,-2), and the radius √54, write the coordinate equation.

5. Solution to c) : Solution to d) : PROCESS 2 SOLUTIONS:

6. PROCESS 3 EXAMPLE: Given the centre (4,-9), and the point (10,-3), write the coordinate equation.

7. PROCESS 3 SOLUTION:

8. PROCESS 4 EXAMPLE: Given the centre (7,12), and the area 21  , write the coordinate equation.

9. PROCESS 4 SOLUTION:

10. PERPENDICULAR DISTANCE PROBLEMS: PROCESS 1 EXAMPLE: Given the point P(3,5) and the line 12x + 4y +3 = 0, find the perpendicular distance.

11. PROCESS 1 SOLUTION:

12. PROCESS 2 EXAMPLE: Given the point P(2,5) and the line 3x + 5y = 8, find the perpendicular distance.

13. PROCESS 2 SOLUTION:

14. PROCESS 3 EXAMPLE: Given the lines -4y + x + 9 = 0 and y - 5x = 12, find the perpendicular distance.

15. PROCESS 3 SOLUTION:

16. LINEAR EQUATION SYSTEM PROBLEM: Solve by Graphing Example: Given this system : Solve graphically. y = x² y = 6 - x²

17. Solve by Graphing solution: y = x² x | y -1 1 ---> P(-1,1) 0 0 ---> P(0,0) 1 1 ---> P(1,1) 2 4 ---> P(2,4) 3 9 ---> P(3,9) 4 16 ---> P(4,16) 5 25 ---> P(5,25) 6 36 ---> P(6,36)

18. y = 6 - x² y = - x² + 6 x | y -1 5 ---> P(-1,5) 0 6 ---> P(0,6) 1 5 ---> P(1,5) 2 2 ---> P(2,2) 3 -3 ---> P(3,-3) 4 -10 ---> P(4,-10) 5 -19 ---> P(5,-19) 6 -30 ---> P(6,30)

19. (-1¾, 3) (1¾, 3) The Solutions are (-1¾, 3) and (1¾, 3) .

20. Solve by Substitution Example: Given this system : Solve using substitution. 12x - 4y = 9 y + 4x = 18

21. Solve by Substitution solution:

22. Solve by Elimination Example: Given this system : 4x + y = 30 -2x + 2y = 10 Solve using elimination.

23. Solve by Elimination solution:

24. BIBLIOGRAPHY: http://www.univie.ac.at/future.media/moe/fplotter/fplotter.html