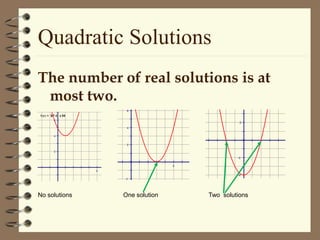
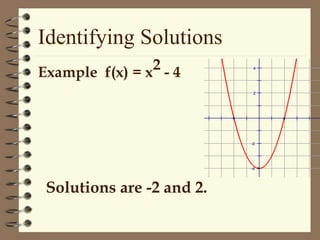
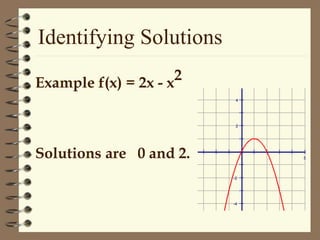
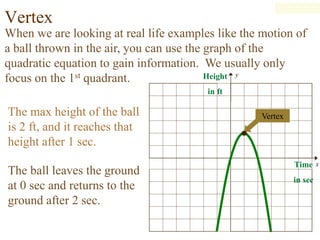
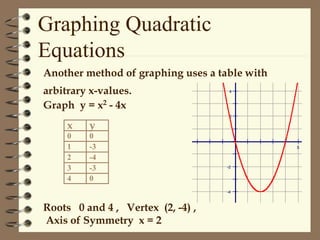
This document discusses solving quadratic equations by graphing. It defines the terms of a quadratic equation and explains that the solutions are the x-intercepts where the graph crosses the x-axis. A quadratic equation will have 0, 1, or 2 real solutions. The graph of a quadratic equation is a parabola with an axis of symmetry. The vertex is the maximum or minimum point, and it can be found using the formula. Graphing involves finding the axis of symmetry, vertex, and using a table to plot additional points to draw the smooth curve.

1. Solving
Quadratic Equations
by Graphing

2. Quadratic Equation
y = ax2 + bx + c
• ax2 is the quadratic term.
• bx is the linear term.
• c is the constant term.
The highest exponent is two;
therefore, the degree is two.

3. Solving Equations
When we talk about solving these
equations, we want to find the value
of x when y = 0. These values, where
the graph crosses the x-axis, are called
the x-intercepts.
These values are also referred to as
solutions, zeros, or roots.

4. The number of real solutions is at
most two.
Quadratic Solutions
No solutions
6
4
2
-2
5
f x  = x2-2 x +5
6
4
2
-2
5
2
-2
-4
-5 5
One solution Two solutions

5. Example f(x) = x2 - 4
Identifying Solutions
4
2
-2
-4
-5
Solutions are -2 and 2.

6. Example f(x) = 2x - x2
Solutions are 0 and 2.
Identifying Solutions
4
2
-2
-4
5

7. Vertex
When we are looking at real life examples like the motion of
a ball thrown in the air, you can use the graph of the
quadratic equation to gain information. We usually only
focus on the 1st quadrant. y
x
VertexThe max height of the ball
is 2 ft, and it reaches that
height after 1 sec.
The ball leaves the ground
at 0 sec and returns to the
ground after 2 sec.
Height
in ft
Time
in sec

8. Graphing a Quadratic Function
Remember, the steps to graphing a parabola in
standard form:
STEP 1: Find the Axis of symmetry using:
STEP 2: Find the vertex
STEP 3: Find two other points and reflect them across
the Axis of symmetry. Then connect the five points
with a smooth curve.
MAKE A TABLE
using x – values close to
the Axis of symmetry.
2
b
a
x 


9. The graph of a quadratic equation is a
parabola.
The roots or zeros are the x-intercepts.
The vertex is the maximum or
minimum point.
All parabolas have an axis of
symmetry.
Graphing Quadratic
Equations

10. Another method of graphing uses a table with
arbitrary x-values.
Graph y = x2 - 4x
Roots 0 and 4 , Vertex (2, -4) ,
Axis of Symmetry x = 2
Graphing Quadratic
Equations
x y
0 0
1 -3
2 -4
3 -3
4 0
4
2
-2
-4
5