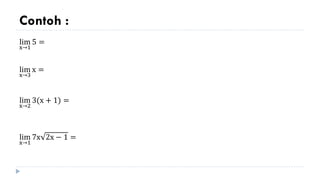
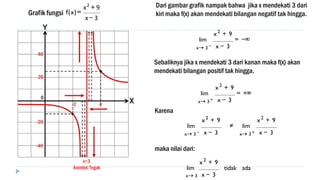
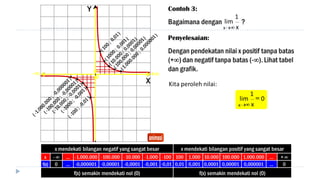
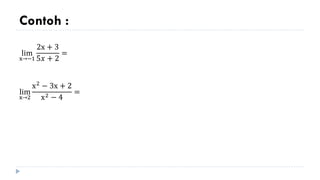
1) The document discusses limit theorems and trigonometric function limits. It introduces basic limit theorems including limits of constants, sums, products, quotients, and composite functions. 2) Examples are provided to illustrate evaluating limits using the limit theorems, including limits approaching positive/negative infinity. 3) The document also discusses evaluating limits of rational functions by factorizing the numerator and denominator into their highest-order terms.

1. MATEMATIKA DASAR
Aswar Amiruddin, ST., MT.

2. Pertemuan 5
 Teorema Limit
 Limit fungsi trigonometri

3. Teorema Limit
Catatan.Teorema merupakan suatu pernyataan yang dapat
dibuktikan kebenarannya, dan kemudian dapat digunakan
sebagai “senjata” kita dlm pemecahan masalah terkait.

4. Teorema Utama Limit
Misalkan k konstanta, n є N, f dan g fungsi yang mempunyai limit
di c
1. lim
x→c
k = k
2. lim
x→c
x = c
3. lim
x→c
kf(x) = k ∗ lim
x→c
f(x)
4. lim
x→c
f(x) ± g(x) = lim
x→c
f(x) ± lim
x→c
g(x)

5. Misalkan k konstanta, n є N, f dan g fungsi yang mempunyai limit
di c
5. lim
x→c
f x . g(x) = lim
x→c
f(x) . lim
x→c
g(x)
6. lim
x→c
f x
g(x)
=
lim
x→c
f(x)
lim
x→c
g(x)
, syarat lim
x→c
g(x) ≠ 0
7. lim
x→c
(f x )n = (lim
x→c
f(x))n
8. lim
x→c
(f x )
1
𝑛 = (lim
x→c
f(x))
1
𝑛
Teorema Utama Limit

6. Contoh :
lim
x→1
5 =
lim
x→3
x =
lim
x→2
3(x + 1) =
lim
x→1
7x 2x − 1 =

7. Contoh :
lim
x→−1
2x + 3
5𝑥 + 2
=
lim
x→2
x2
− 3x + 2
x2 − 4
=

10. Limit tak hingga
 Tinjau fungsi 𝑓 𝑥 =
1
𝑥
, dengan x ≠ 0.
 Apa yang terjadi jika nilai x dekat dengan 0?
 Berapakah nilai limit 𝑓 di 0, ada aau tidak ada?
 Misalkan 𝑓 terdefinisi di sekitar x = c, dapat kita tuliskan
lim
x→c+
f x = +∞ lim
x→c−
f x = −∞

11. Dari gambar grafik nampak bahwa jika x mendekati 3 dari
kiri maka f(x) akan mendekati bilangan negatif tak hingga.
Sebaliknya jika x mendekati 3 dari kanan maka f(x) akan
mendekati bilangan positif tak hingga.
Karena
maka nilai dari:
-
=
-
+
-
→ 3
x
9
x
lim
2
3
x
+
=
-
+
+
→ 3
x
9
x
lim
2
3
x
3
x
9
x
lim
3
x
9
x
lim
2
3
x
2
3
x -
+

-
+
+
- →
→
ada
tidak
3
x
9
x
lim
2
3
x -
+
→

13. Bagi pangkat
tertinggi
....
1
x
x
2
1
x
x
3
lim
x
=






+
-
-

→
)
1
x
)(
1
x
(
)
1
x
(
x
2
)
1
x
(
x
3
lim
x +
-
-
-
+
=

→
1
x
x
2
x
2
x
3
x
3
lim 2
2
2
x -
+
-
+
=

→
1
x
x
5
x
lim 2
2
x -
+
=

→
2
2
2
2
2
2
x
1
x
x
x
x
5
x
x
x
lim
-
+
=

→
1
0
1
0
1
1
1
lim
2
x
1
x
5
x
=
-
+
=
-
+
=

→
1
1
x
x
2
1
x
x
3
lim
x
=






+
-
-

→
Contoh :