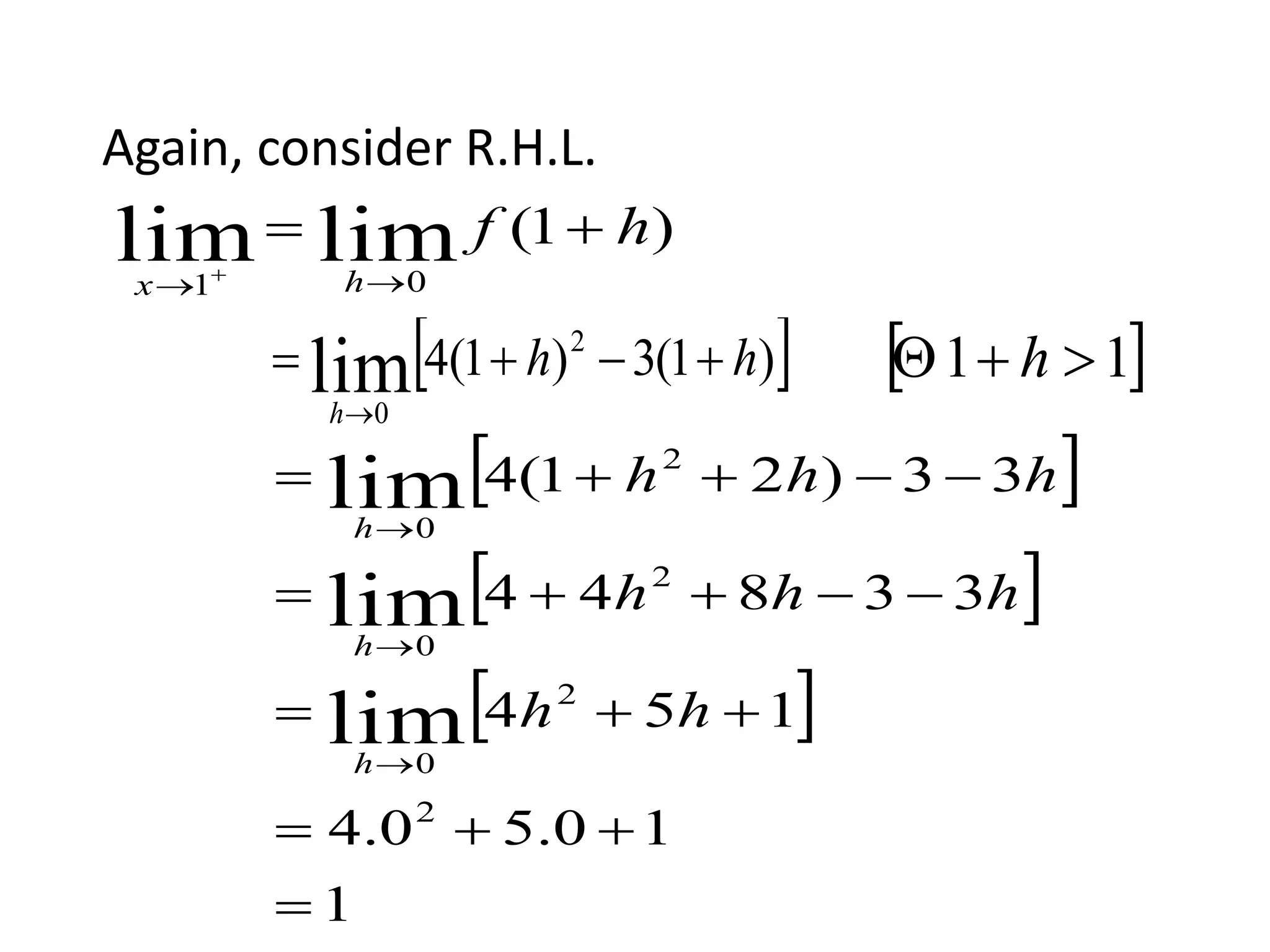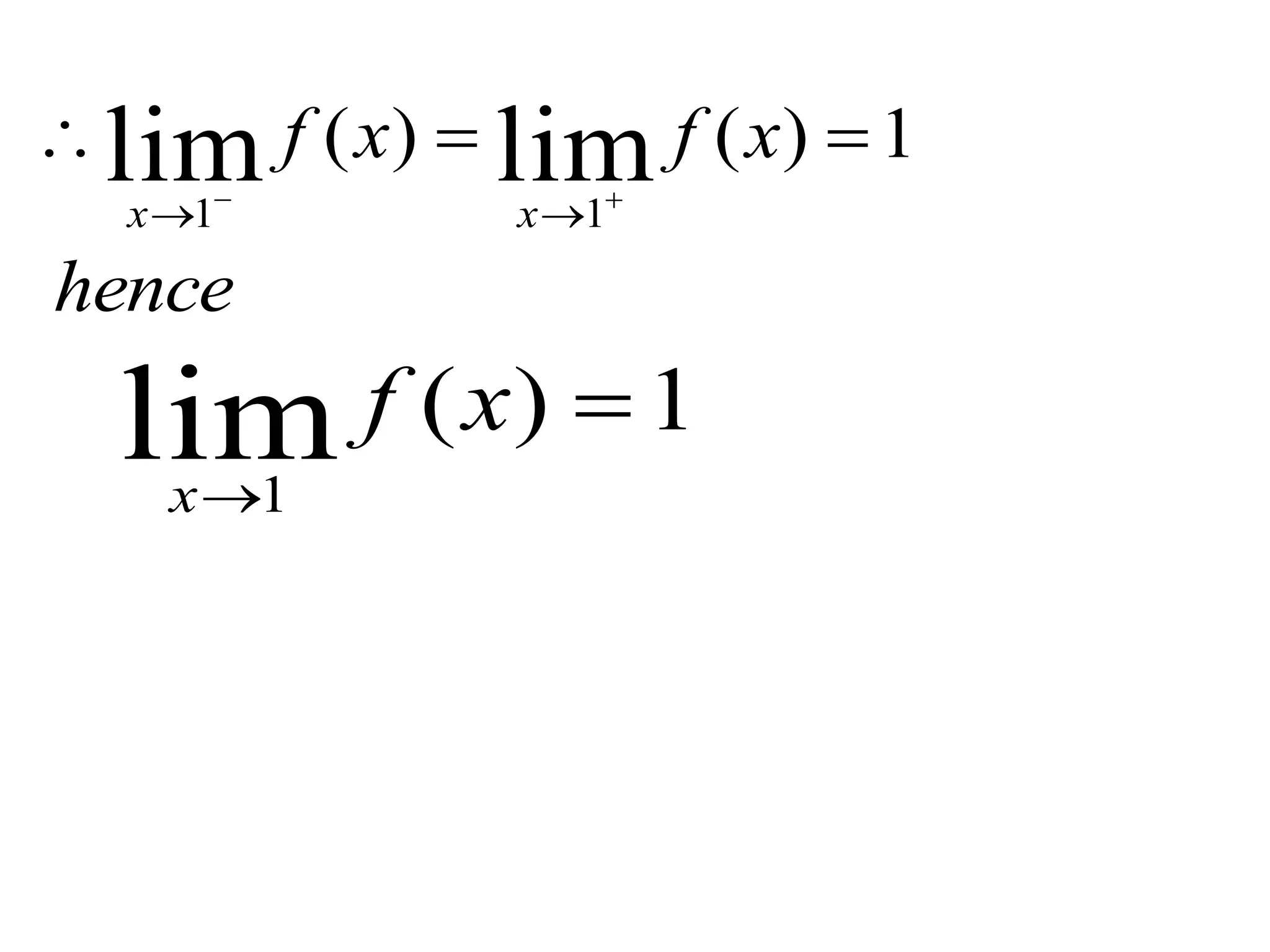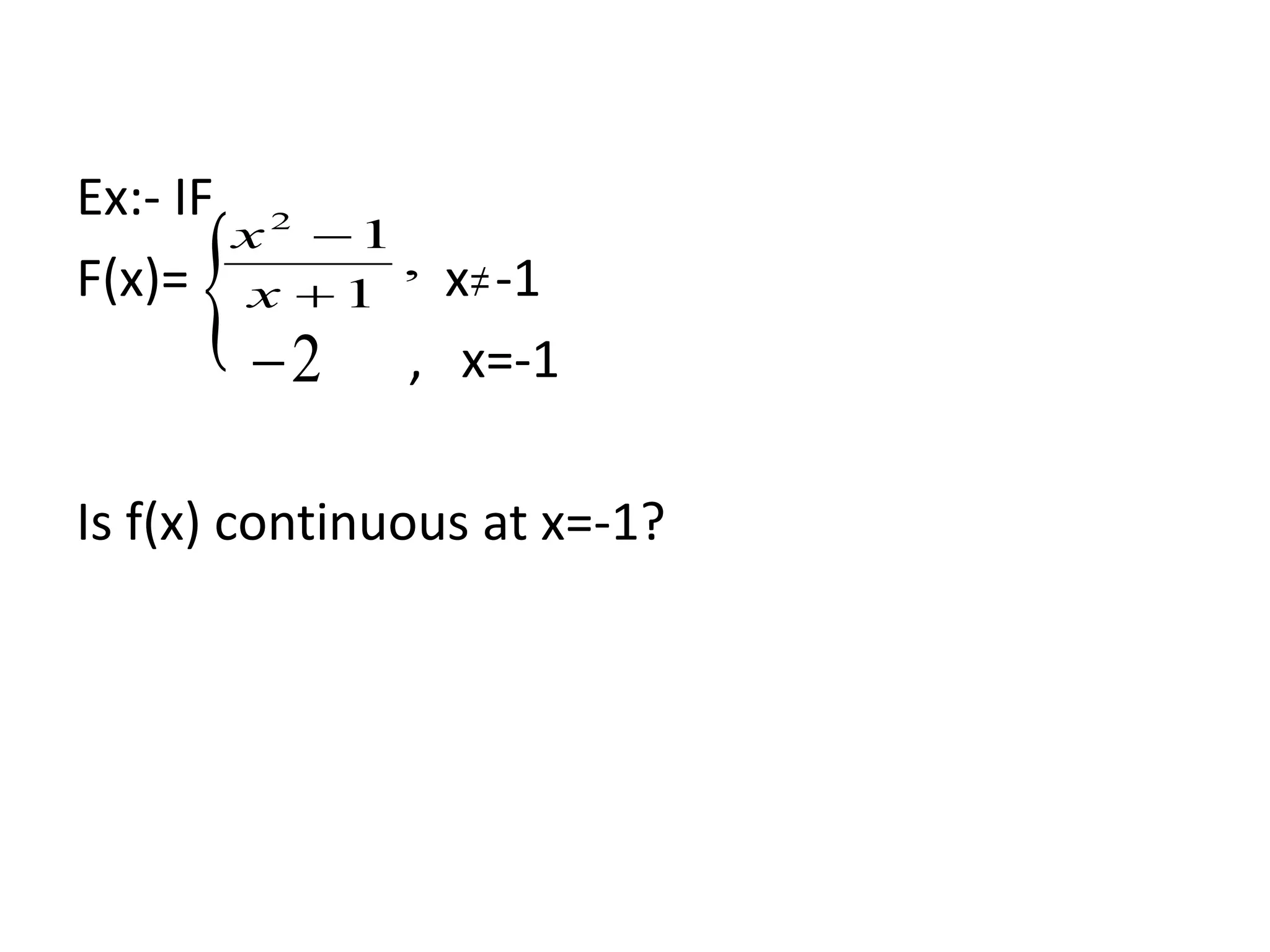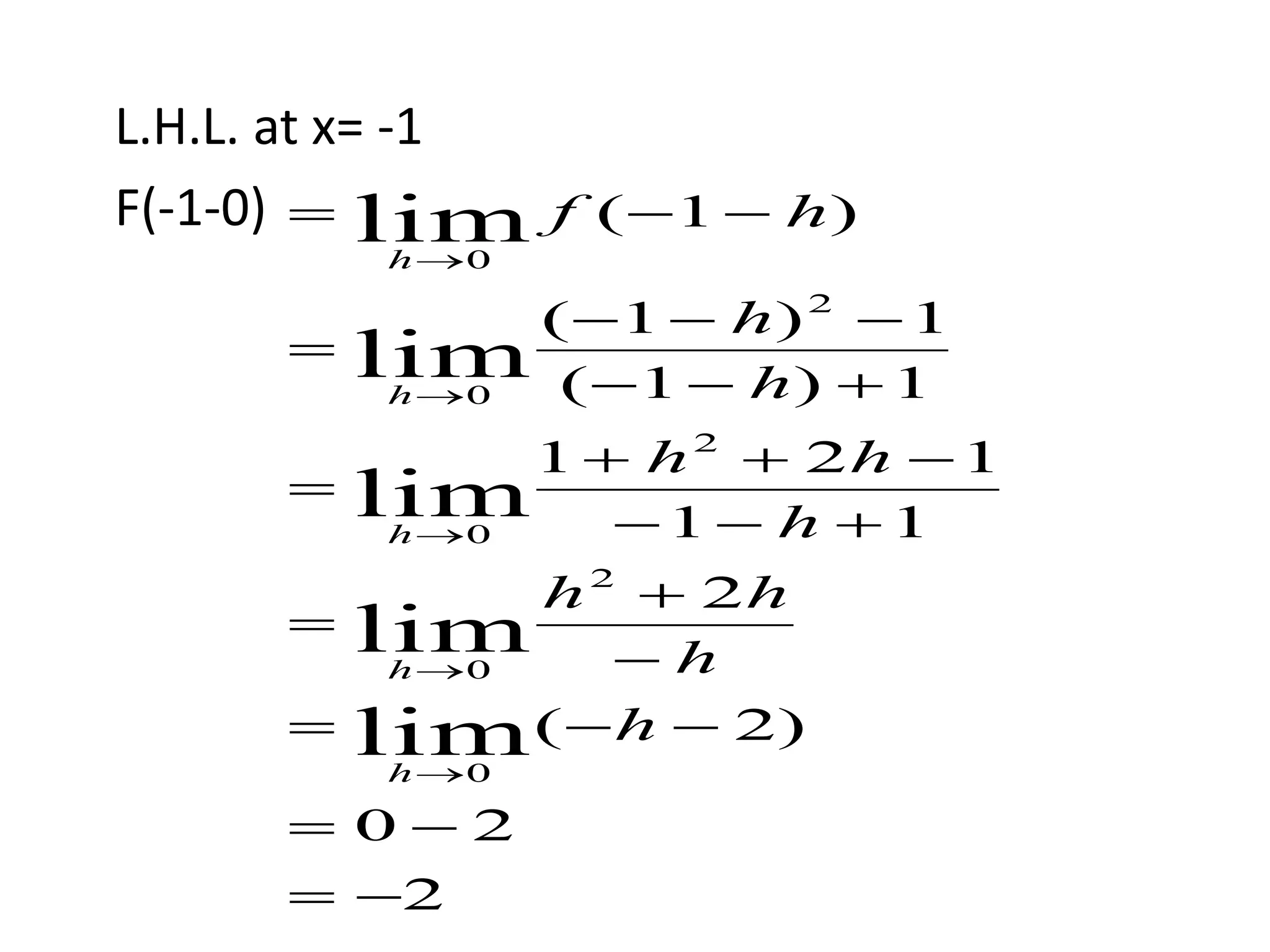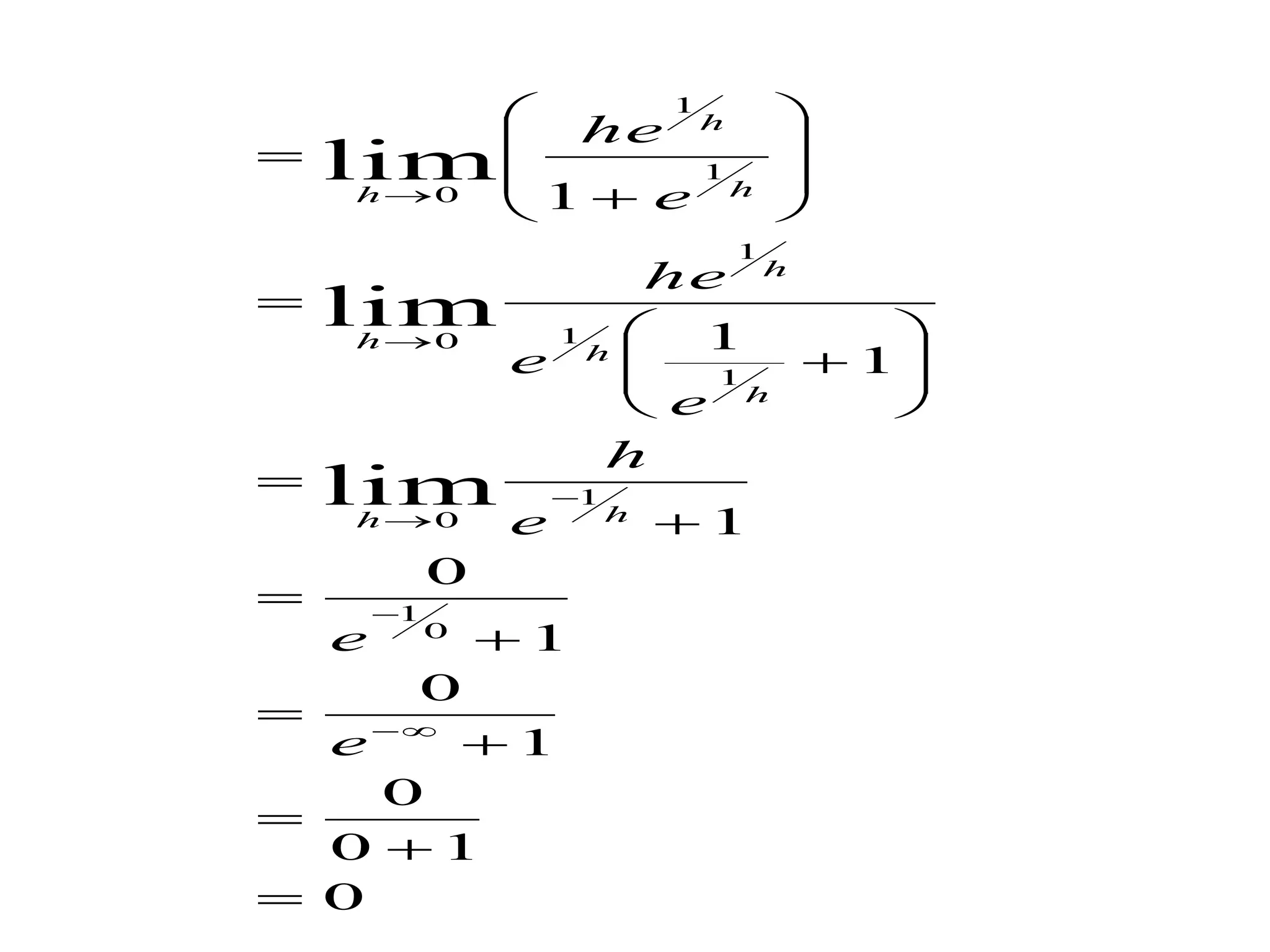The document presents a comprehensive overview of the mathematical concepts of limits and continuity, focusing on definitions for left-hand and right-hand limits. It explains the conditions under which a function is considered defined or undefined at a given point, as well as providing examples to illustrate the concepts. Additionally, it explores the concept of continuity in functions and includes examples of determining continuity at specific points.

1. Shri Shankaracharya Mahavidyalaya
JUNWANI,BHILAI NAGAR (C.G)
TOPIC:-LIMIT AND CONTINUITY
Presented by:
Mrs. Preeti Shrivastava

2. CONTENT
(1) DEFINATION OF LIMIT.
(2) DEFINACTION OF LEFT HAND
LIMIT.
(3) DEFINACTION OF RIGHT HAND
LIMIT.
(4) EXAMPLE.
(5) CONTINUITY.
(6) SOME EXAMPLES.

3. LIMITS
DEFINACTION:- Let f(x) be a function
of the variable x, then the value
of f(x) at x=a, i.e. for some value
`a’ of x is denoted by f(a). The
value of f(a) may be of two kinds.

4. (i) A definite and finite quantity:-
In this case the value of f(x) is said
to be defined at x=a.
(ii) An indefinite and indeterminate
quantity:-
In this case the value of f(x) is said
to be undefined at x=a.

5. LEFT HAND LIMIT
DEFINITION:- A function f(x) is sadi to
tend to `l’ as a tends to a through the
values less than a (or from left), if for
any given there exists a such
that.
i.e. for every f(x)
0 0
 ,,aax     ll ,
  lxfaxa )(

6. Symbolicelly, we write:-
Or
Or f(a-0)=
And is called the left hand limit (L.H.L.)
lxf
ax


)(lim0
lxf
ax


)(lim
l

7. RIGHT HEND LIMIT
DEFINITION:- A function f(x) is said to be tend to
limit l as x tends to a, through the values
greater than a (or form right), if for every
there exist a such that
i.e. for every
Symbolically, we write:-
0
0
  lxfaxa )(
),()(),,(   llxfaax
0)(lim0


xf
ax

8. Or f(a+0) =
And is called the right hand limit (R.H.L.)
Ex:- If
F(x)= when x<1
when x>1
Find if it exist.
lxf
ax


)(lim
 ,23 x
,34
2
xx 
),(lim1
xf
x
l

9. SOLUCTION:- consider the L.H.L.
)1()( limlim 01
hfxf
hx


 
 
0
01
0.31
)31(
233
2)1(3
lim
lim
lim
0
0
0









h
h
h
h
h
h

10. Again, consider R.H.L.
)1(limlim 01
hf
hx

 
 )1(3)1(4 2
0
lim hh
h


 11  h
 
 
 
1
10.50.4
154
33844
33)21(4
2
2
0
2
0
2
0
lim
lim
lim








hh
hhh
hhh
h
h
h

11. 1)()( limlim 11



xfxf
xx
hence
1)(lim1


xf
x

12. CONTINUITY:-
The intuitive concept of continuity of a
function is derived from its geometrical
construction. If the graph of the function
y=f(x) is curve which does not break at the
point x=a then the function y=f(x) is called
continuous at x=a.
If the graph of the function break at some
point then this point is called the point of
discontinuity.

13. Ex:- IF
F(x)= x -1
, x=-1
Is f(x) continuous at x=-1?
 ,
1
12


x
x
2


14. Soluction L:- R.H.L. at x=-1
F(-1+0)
2
20
2
)2(
2
11
)121(
1)1(
1)1(
)1(
lim
lim
lim
lim
lim
lim
0
0
2
0
2
0
2
0



















h
h
h
hh
h
hh
h
h
hf
h
h
h
h
oh
h

15. L.H.L. at x= -1
F(-1-0)
2
20
)2(
2
11
121
1)1(
1)1(
)1(
lim
lim
lim
lim
lim
0
2
0
2
0
2
0
0


















h
h
hh
h
hh
h
h
hf
h
h
h
h
h

16. Again when x=-1, then f(x)= -2
f(x)=2
Since f(-1-0)= f(-1)
Hence the given function is continuous at x= -1


17. The following function for continuity at the
origin.
f(x)= , if x 0
, if x = 0
SOLUCTION:- Here f(0)=0
R.H.L. f(0+0)


















)(
11
)0(
1)0(
lim
)0(lim
0
0
ho
e
h
eh
hf
h
h
0
1
1
1
x
x
e
xe


18. 0
10
0
1
0
1
0
1
1
1
1
0
1
1
0
1
1
1
0
1
1
0
lim
lim
lim



































e
e
e
h
e
e
he
e
he
hh
h
h
h
h
h
h
h

19. L.H.L. = F(0-0)
since f(0+0) = f(0),so f(x) is continuous at x=0.
0
01
0
1
.0
1
1
)0(
)0(
0
1
0
1
1
1
0
)0(
1
)0(
1
0
0
lim
lim
lim





























e
e
e
he
e
eh
hf
h
h
h
h
h
h
h

20. THANK YOU