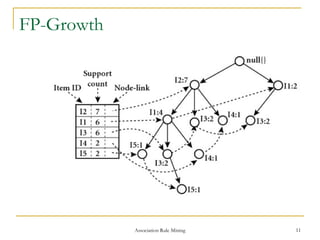
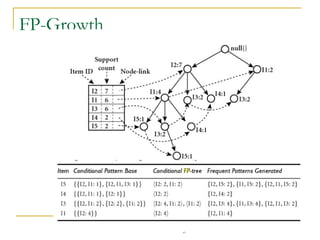
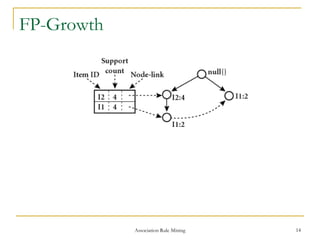
Association rule mining is used to find relationships between items in transactional datasets. It involves finding frequent itemsets that satisfy minimum support and generating association rules from these itemsets that satisfy minimum confidence. FP-Growth is an efficient algorithm for mining frequent itemsets without candidate generation by constructing a frequent-pattern tree and mining it recursively. It avoids multiple database scans and generates far fewer candidates than Apriori, making it faster and more scalable.

1. Association Rule Mining 1
Association Rule Mining

2. Association Rule Mining 2
Generating Association Rules from
Frequent Itemsets
 Strong association rules satisfy both minimum
support and minimum confidence levels
 Confidence (A ⇒ B)
= P(B / A )
= support_count(A U B) / support_count(A)
 Association rules
 For each frequent itemset l, generate all non-empty
subsets of l
 For every non-empty subset s of l, output s ⇒ (l-s) if
sup_count(l) / sup_count(s) >= min_conf

3. Association Rule Mining 3
Example
I = {I1, I2, I5} Confidence Threshold : 70%
Non empty subsets: {I1, I2}, {I1, I5}, {I2, I5}
{I1}, {I2}, {I5}
I1 ∧ I2 ⇒ I5, confidence = 2 /4 = 50%
I1 ∧ I5 ⇒ I2, confidence = 2 /2 = 100%
I2 ∧ I5 ⇒ I1, confidence = 2 /2 = 100%
I1 ⇒ I2 ∧ I5, confidence = 2 /6 = 33%
I2 ⇒ I1 ∧ I5, confidence = 2 /7 = 29%
I5 ⇒ I1 ∧ I2, confidence = 2 /2 = 100%

4. Association Rule Mining 4
Improving the Efficiency of Apriori
 Hash based technique
 Transaction reduction
 A transaction which does not contain k frequent
itemsets cannot contain k+1 frequent itemsets
 Partitioning
 Sampling
 Dynamic itemset counting
 Start points

5. Association Rule Mining 5
Hash Based Technique
Bucket
Address
0 1 2 3 4 5 6
Bucket
count
2 2 4 2 2 4 4
Bucket
Content
s
{I1,I4}
{I3,I5}
{I1,I5}
{I1,I5}
{I2,I3}
{I2,I3}
{I2,I3}
{I2,I3}
{I2,I4}
{I2,I4}
{I2,I5}
{I2,I5}
{I1,I2}
{I1,I2}
{I1,I2}
{I1,I2}
{I1,I3}
{I1,I3}
{I1,I3}
{I1,I3}
H(x,y) = (x*10+y)%7

6. Association Rule Mining 6
Partition: Scan Database Only Twice
 Any itemset that is potentially frequent in DB
must be frequent in at least one of the
partitions of DB
 Scan 1: partition database and find local frequent
patterns
 Scan 2: consolidate global frequent patterns

7. Association Rule Mining 7
Sampling for Frequent Patterns
 Select a sample of original database, mine frequent
patterns within sample using Apriori
 Can use a lower support threshold
 Scan database once to verify frequent itemsets
found in sample
 Scan database again to find missed frequent
patterns

8. Association Rule Mining 8
Bottleneck of Frequent-pattern Mining
 Multiple database scans are costly
 Mining long patterns needs many passes of
scanning and generates lots of candidates
 To find frequent itemset i1i2…i100
 # of scans: 100
 # of Candidates: = 2100
-1 = 1.27*1030
 Bottleneck: candidate-generation-and-test
 Avoid candidate generation

9. Association Rule Mining 9
Mining Frequent Patterns Without
Candidate Generation
 FP Growth
 Divide and Conquer technique
 FP-Tree
 Grow long patterns from short ones using local
frequent items

10. Association Rule Mining 10
FP-tree from a Transaction Database -
Example
Database TDB
Tid Items
T100 I1,I2,I5
T200 I2,I4
T300 I2,I3
T400 I1, I2, I4
T500 I1, I3
T600 I2, I3
T700 I1, I3
T800 I1, I2, I3, I5
T900 I1, I2, I3
Minimum Support = 2 / 9 = 22%

11. FP-Growth
Association Rule Mining 11

12. FP-Growth
 For each frequent length-1 pattern(Suffix
pattern):
 Construct conditional pattern base (Sub-database
consisting of set of prefix paths co-occurring with
suffix)
 Construct conditional FP-tree and mine
recursively
 Generate all combinations of frequent patterns by
combing with suffix
Association Rule Mining 12

13. FP-Growth
Association Rule Mining 13

14. FP-Growth
Association Rule Mining 14

15. Association Rule Mining 15
Algorithm
Input: A transaction db D; min_sup
Output: Frequent patterns
Construction of FP-Tree
1. Scan database, collect frequent items F and sort in descending
order of support
2. Create root of FP-tree labeled null
For each Trans, sort in descending order [p|P]
Insert_tree([p|P],T)
If T has a child N = p, increment count
else create new node with count 1 and set parent and node
links
If P is non-empty call insert_tree(P,N) recursively

16. Association Rule Mining 16
Algorithm
Procedure FP_growth (Tree, a)
If Tree contains a single path P then
for each combination of nodes- b generate b ∪ a with support = min.
support of nodes in b
else for each xi in the header of the Tree
{
generate pattern b = xi ∪ a with support = xi.support
construct b’s conditional pattern base and b’s conditional FP_tree
Treeb
if Treeb < > NULL then call FP_growth(Treeb, b)
}

17. Association Rule Mining 17
Features
 Finds long frequent patterns by looking for shorter
ones recursively
 Items in frequency descending order: the more
frequently occurring, the more likely to be shared
 Main-memory based FP-tree
 Efficient and scalable
 Faster than Apriori