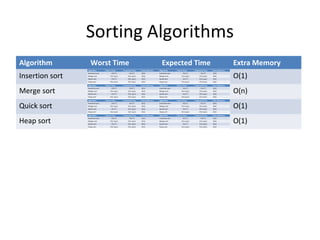
The document discusses quicksort, an efficient sorting algorithm. It begins with a review of insertion sort and merge sort. It then presents the quicksort algorithm, including choosing a pivot, partitioning the array around the pivot, and recursively sorting subarrays. Details are provided on the partition process with examples. Analysis shows quicksort has worst-case time complexity of O(n^2) but expected complexity of O(nlogn) with only O(1) extra memory. Strict proofs are outlined for the worst and expected cases. The document concludes with notes on implementing quicksort in Java for practice.

1. Design and Analysis of Algorithms
Quicksort
Haidong Xue
Summer 2012, at GSU

2. Review of insertion sort and merge sort
• Insertion sort
– Algorithm
– Worst case number of comparisons = O(?)
• Merge sort
– Algorithm
– Worst case number of comparisons = O(?)

3. Sorting Algorithms
Algorithm Worst Time Expected Time Extra Memory
Insertion sort O(1)
Merge sort O(n)
Quick sort O(1)
Heap sort O(1)
Algorithm Worst Time Expected Time Extra Memory
Insertion sort O(1)
Merge sort O(n)
Quick sort O(1)
Heap sort O(1)

4. Quicksort Algorithm
• Input: A[1, …, n]
• Output: A[1, .., n], where A[1]<=A[2]…<=A[n]
• Quicksort:
1. if(n<=1) return;
2. Choose the pivot p = A[n]
3. Put all elements less than p on the left; put all elements lager
than p on the right; put p at the middle. (Partition)
4. Quicksort(the array on the left of p)
5. Quicksort(the array on the right of p)

5. Quicksort Algorithm
• Quicksort example
2 8 7 1 3 5 6 4
2 871 3 5 64
2 871 3 5 64
Current pivots
Previous pivots
Quicksort
Hi, I am nothing Nothing Jr.
Nothing 3rd
2 871 3 5 64
2 871 3 5 64
2 871 3 5 64

6. Quicksort Algorithm
• More detail about partition
• Input: A[1, …, n] (p=A[n])
• Output: A[1,…k-1, k, k+1, … n], where A[1, …, k-1]<A[k] and A[k+1, … n] >
A[k], A[k]=p
• Partition:
1. t = the tail of smaller array
2. from i= 1 to n-1{
3. if(A[i]<p) {
4. exchange A[t+1] with A[i];
5. update t to the new tail;
6. }
7. exchange A[t+1] with A[n];

7. Quicksort Algorithm
• Partition example
2 8 7 1 3 5 6 4
2 8 7 1 3 5 6 4
2 8 7 1 3 5 6 4
tail
2 8 7 1 3 5 6 4
tail
tail
tail
Exchange 2 with A[tail+1]
Do nothing
Do nothing

8. Quicksort Algorithm
• Partition example
2 8 7 1 3 5 6 4
2 871 3 5 6 4
2 8 71 3 5 6 4
tail
tail
Exchange 1 with A[tail+1]
tail
Exchange 3 with A[tail+1]
Do nothing
2 8 71 3 5 6 4
tail
Do nothing
2 871 3 5 64 Final step: exchange A[n]
with A[tail+1]

9. Quicksort Algorithm
The final version of quick sort:
Quicksort(A, p, r){
if(p<r){ //if(n<=1) return;
q = partition(A, p, r); //small ones on left;
//lager ones on right
Quicksort(A, p, q-1);
Quicksort(A, q+1, r);
}
}

10. Analysis of Quicksort
Time complexity
– Worst case
– Expected
Space complexity - extra memory
– 0 = O(1)

11. Analysis of Quicksort
Worst case
• The most unbalanced one ---
• Is it the worst case?
• Strict proof
Expected time complexity
• Strict proof
•

12. Strict proof of the worst case time
complexity
Proof that
1. When n=1, (1)=
2. Hypothesis: when
induction statement: when
•

13. Strict proof of the worst case time
complexity
Since ,
+
•

14. Strict proof of the expected time complexity
• Given A[1, …, n], after sorting them to , the
chance for 2 elements, A[i] and A[j], to be
compared is .
• The total comparison is calculated as:
•

15. Java implementation of Quicksort
• Professional programmers DO NOT implement sorting
algorithms by themselves
• We do it for practicing algorithm implementation
techniques and understanding those algorithms
• Code quicksort
– Sort.java // the abstract class
– Quicksort_Haydon.java // my quicksort implementation
– SortingTester.java // correctness tester