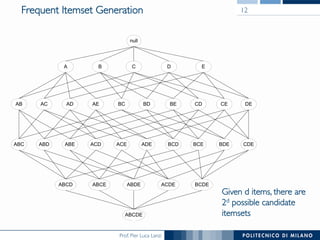
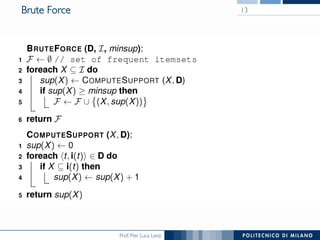
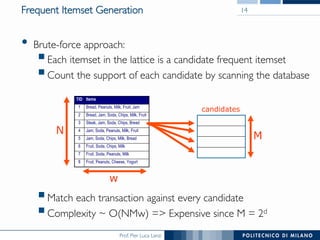
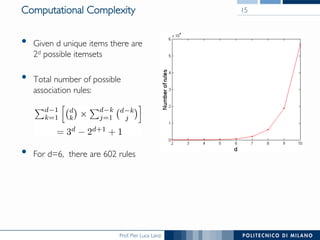
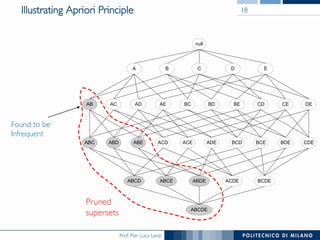
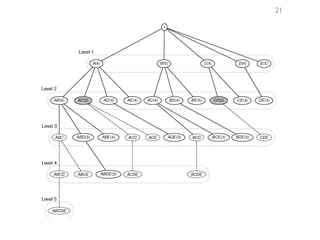
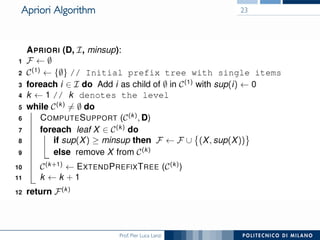
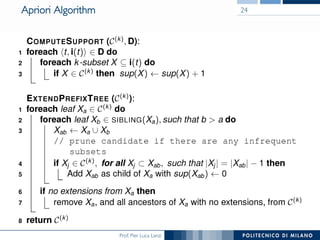
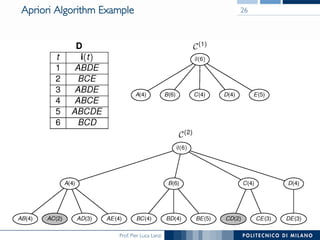
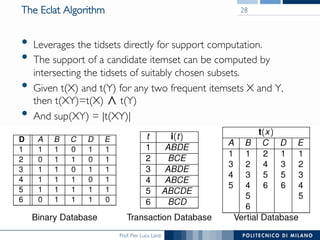
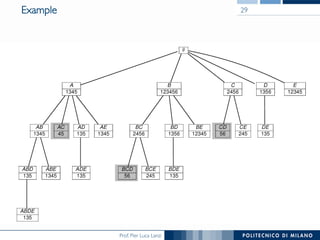
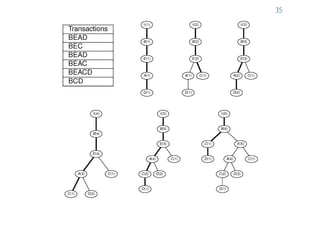
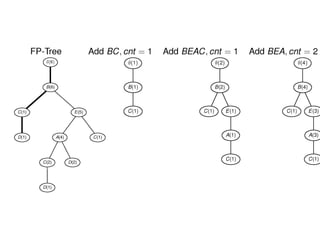
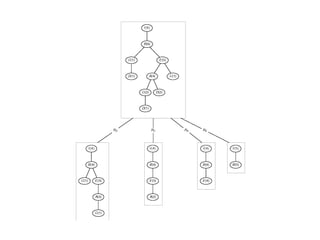
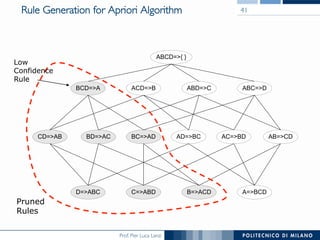
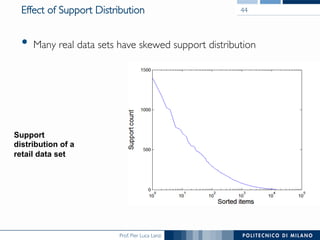
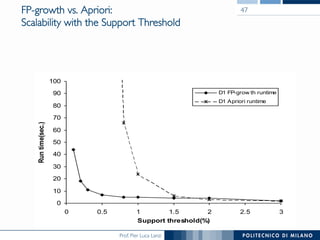
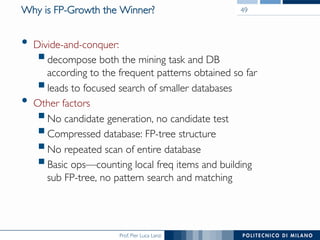
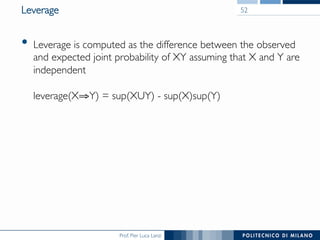
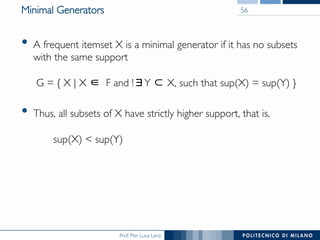
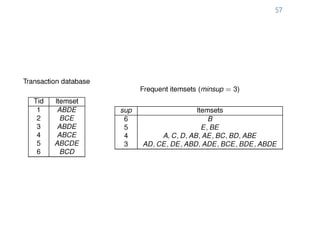
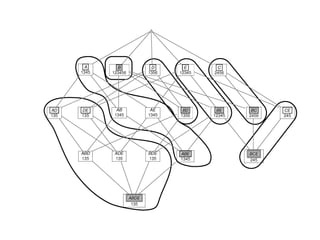
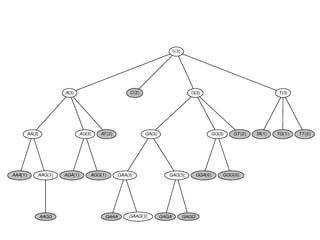
The document provides an overview of association rule mining, including frequent patterns, itemsets, and the mining process. It discusses the goals, algorithms such as Apriori and FP-Growth, and strategies for generating rules efficiently while managing computational complexity. Additionally, it highlights evaluation metrics like support and confidence, as well as techniques to optimize mining operations.