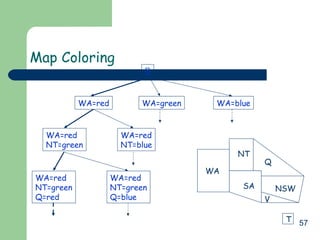
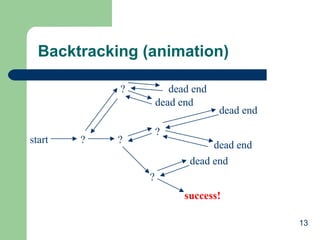
The document discusses various backtracking algorithms and problems. It begins with an overview of backtracking as a general algorithm design technique for problems that involve traversing decision trees and exploring partial solutions. It then provides examples of specific problems that can be solved using backtracking, including the N-Queens problem, map coloring problem, and Hamiltonian circuits problem. It also discusses common terminology and concepts in backtracking algorithms like state space trees, pruning nonpromising nodes, and backtracking when partial solutions are determined to not lead to complete solutions.

1. BackTracking Algorithms
Briana B. Morrison
With thanks to Dr. Hung

2. 2
Topics
 What is Backtracking
 N-Queens Problem
 Sum of Subsets
 Graph Coloring
 Hamiltonian Circuits
 Other Problems

3. 3
Algorithm Design
Human
Problems Result
Input Data
Structures Processing
Output Data
Structures
Computer
Algorithms

4. 4
Algorithm Design …
For a problem? What is an Optimal Solution?
• Minimum CPU time
• Minimum memory
Example: Given 4 numbers, sort it to nonincreasing order.
Method 1: Sequential comparison
1. Find the largest (3 comparisons)
2. Find the second largest (2 comparisons)
3. Find the third largest (1 comparisons)
4. Find the fourth largest
A total of 6 comparisons

5. 5
Algorithm Design …
For a problem? What is an Optimal Solution?
• Minimum CPU time
• Minimum memory
Example: Given 4 numbers, sort it to nonincreasing order.
Method 2: Somewhat clever method
a1 a2 a3 a4
a2 a4
a4
a2 a3
a3
a2 a3
a2
a1 a3
a3 or a1
(4 comparisons)
(5 comparisons)

6. 6
Backtracking Problems
 Find your way through the well-known maze of
hedges by Hampton Court Palace in England? Until
you reached a dead end.
 0-1 Knapsack problem – exponential time
complexity.
 N-Queens problem.

7. 7
Backtracking
 Suppose you have to make a series of
decisions, among various choices, where
– You don’t have enough information to know what
to choose
– Each decision leads to a new set of choices
– Some sequence of choices (possibly more than
one) may be a solution to your problem
 Backtracking is a methodical way of trying out
various sequences of decisions, until you find
one that “works”

8. 8
Introduction
 Backtracking is used to solve problems in which a sequence
of objects is chosen from a specified set so that the sequence
satisfies some criterion.
 Backtracking is a modified depth-first search of a
tree.
 Backtracking involves only a tree search.
 Backtracking is the procedure whereby, after
determining that a node can lead to nothing but dead
nodes, we go back (“backtrack”) to the node’s parent
and proceed with the search on the next child.

9. 9
Introduction …
 We call a node nonpromising if when visiting the node
we determine that it cannot possibly lead to a solution.
Otherwise, we call it promising.
 In summary, backtracking consists of
– Doing a depth-first search of a state space tree,
– Checking whether each node is promising, and, if it is
nonpromising, backtracking to the node’s parent.
 This is called pruning the state space tree, and the
subtree consisting of the visited nodes is called the
pruned state space tree.

10. 10
Solving a maze
 Given a maze, find a path from start to finish
 At each intersection, you have to decide between three or fewer
choices:
– Go straight
– Go left
– Go right
 You don’t have enough information to choose correctly
 Each choice leads to another set of choices
 One or more sequences of choices may (or may not) lead to a
solution
 Many types of maze problem can be solved with backtracking

11. 11
Coloring a map
 You wish to color a map with
not more than four colors
– red, yellow, green, blue
 Adjacent countries must be in
different colors
 You don’t have enough information to choose colors
 Each choice leads to another set of choices
 One or more sequences of choices may (or may not)
lead to a solution
 Many coloring problems can be solved with
backtracking

12. 12
Solving a puzzle
 In this puzzle, all holes but one are filled
with white pegs
 You can jump over one peg with
another
 Jumped pegs are removed
 The object is to remove all but the last peg
 You don’t have enough information to jump correctly
 Each choice leads to another set of choices
 One or more sequences of choices may (or may not)
lead to a solution
 Many kinds of puzzle can be solved with backtracking

13. 13
Backtracking (animation)
start ?
?
dead end
dead end
?
?
dead end
dead end
?
success!
dead end

14. 14
N-Queens Problem
 Try to place N queens on an N * N board
such that none of the queens can attack
another queen.
 Remember that queens can move
horizontally, vertically, or diagonally any
distance.
 Let’s consider the 8 queen example…

15. 15
The 8-Queens Example

16. 16
0
1
2
3
4
5
6
7
0 1 2 3 4 5 6 7

17. 17
A t (4 ,4 ) a t t a c k fro m (0 ,0 ) A t (5 ,4 ) a t t a c k fro m (2 ,1 ) A t (6 ,4 ) a t t a c k fro m (4 ,2 ) A t (7 ,4 ) s u c c e s s
0
1
2
3
4
5
6
7
0 1 2 3 4 5 6 7

18. 18
Let’s look at it run

19. 19
Terminology I
There are three kinds of
nodes:
A tree is composed of nodes
The (one) root node
Internal nodes
Leaf nodes
Backtracking can be thought of
as searching a tree for a
particular “goal” leaf node

20. 20
Terminology II
 Each non-leaf node in a tree is a parent of
one or more other nodes (its children)
 Each node in the tree, other than the root,
has exactly one parent
parent
children
parent
children
Usually, however,
we draw our trees
downward, with
the root at the top

21. 21
Real and virtual trees
 There is a type of data structure called a tree
– But we are not using it here
 If we diagram the sequence of choices we
make, the diagram looks like a tree
– In fact, we did just this a couple of slides ago
– Our backtracking algorithm “sweeps out a tree” in
“problem space”

22. 22
The backtracking algorithm
 Backtracking is really quite simple--we
“explore” each node, as follows:
 To “explore” node N:
1. If N is a goal node, return “success”
2. If N is a leaf node, return “failure”
3. For each child C of N,
3.1. Explore C
3.1.1. If C was successful, return “success”
4. Return “failure”

23. 23
Sum-of-Subsets problem
 Recall the thief and the 0-1 Knapsack problem.
 The goal is to maximize the total value of the stolen
items while not making the total weight exceed W.
 If we sort the weights in nondecreasing order before
doing the search, there is an obvious sign telling us that
a node is nonpromising.

24. 24
Sum-of-Subsets problem …
 Let total be the total weight of the remaining weights, a
node at the ith level is nonpromising if
weight + total> W

25. 25
Example
 Say that our weight values are 5, 3, 2, 4, 1
 W is 8
 We could have
– 5 + 3
– 5 + 2 + 1
– 4 + 3 + 1
 We want to find a sequence of values that
satisfies the criteria of adding up to W

26. 26
Tree Space
 Visualize a tree in which the children of the root
indicate whether or not value has been picked (left is
picked, right is not picked)
 Sort the values in non-decreasing order so the
lightest value left is next on list
 Weight is the sum of the weights that have been
included at level i
 Let weight be the sum of the weights that have been
included up to a node at level i. Then, a node at the
ith level is nonpromising if
weight + wi+1 > W

27. 27
Sum-of-Subsets problem …
 Example: Show the pruned state space tree when
backtracking is used with n = 4, W = 13, and w1 = 3,
w2 = 4, w3 = 5, and w4 = 6. Identify those
nonpromising nodes.

28. 28
Full example: Map coloring
 The Four Color Theorem states that any map on
a plane can be colored with no more than four
colors, so that no two countries with a common
border are the same color
 For most maps, finding a legal coloring is easy
 For some maps, it can be fairly difficult to find a
legal coloring
 We will develop a complete Java program to
solve this problem

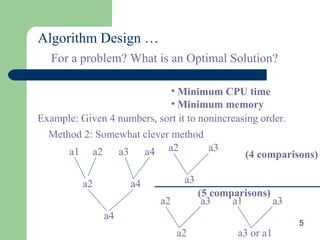
29. 29
Data structures
 We need a data structure that is easy to work with,
and supports:
– Setting a color for each country
– For each country, finding all adjacent countries
 We can do this with two arrays
– An array of “colors”, where countryColor[i] is the color of
the ith
country
– A ragged array of adjacent countries, where map[i][j] is the
jth
country adjacent to country i
 Example: map[5][3]==8 means the 3th
country adjacent to
country 5 is country 8

30. 30
Creating the map 0 1
4
2 3
6
5int map[][];
void createMap() {
map = new int[7][];
map[0] = new int[] { 1, 4, 2, 5 };
map[1] = new int[] { 0, 4, 6, 5 };
map[2] = new int[] { 0, 4, 3, 6, 5 };
map[3] = new int[] { 2, 4, 6 };
map[4] = new int[] { 0, 1, 6, 3, 2 };
map[5] = new int[] { 2, 6, 1, 0 };
map[6] = new int[] { 2, 3, 4, 1, 5 };
}

31. 31
Setting the initial colors
static final int NONE = 0;
static final int RED = 1;
static final int YELLOW = 2;
static final int GREEN = 3;
static final int BLUE = 4;
int mapColors[] = { NONE, NONE, NONE, NONE,
NONE, NONE, NONE };

32. 32
The main program
(The name of the enclosing class is ColoredMap)
public static void main(String args[]) {
ColoredMap m = new ColoredMap();
m.createMap();
boolean result = m.explore(0, RED);
System.out.println(result);
m.printMap();
}

33. 33
The backtracking method
boolean explore(int country, int color) {
if (country >= map.length) return true;
if (okToColor(country, color)) {
mapColors[country] = color;
for (int i = RED; i <= BLUE; i++) {
if (explore(country + 1, i)) return true;
}
}
return false;
}

34. 34
Checking if a color can be used
boolean okToColor(int country, int color) {
for (int i = 0; i < map[country].length; i++) {
int ithAdjCountry = map[country][i];
if (mapColors[ithAdjCountry] == color) {
return false;
}
}
return true;
}

35. 35
Printing the results
void printMap() {
for (int i = 0; i < mapColors.length; i++) {
System.out.print("map[" + i + "] is ");
switch (mapColors[i]) {
case NONE: System.out.println("none"); break;
case RED: System.out.println("red"); break;
case YELLOW: System.out.println("yellow"); break;
case GREEN: System.out.println("green"); break;
case BLUE: System.out.println("blue"); break;
}
}
}

36. 36
Recap
 We went through all the countries recursively, starting
with country zero
 At each country we had to decide a color
– It had to be different from all adjacent countries
– If we could not find a legal color, we reported failure
– If we could find a color, we used it and recurred with
the next country
– If we ran out of countries (colored them all), we
reported success
 When we returned from the topmost call, we were done

37. 37
Hamiltonian Circuits Problem
 Hamiltonian circuit (tour) of a graph is a path
that starts at a given vertex, visits each
vertex in the graph exactly once, and ends at
the starting vertex.

38. 38
State Space Tree
 Put the starting vertex at level 0 in the tree
 At level 1, create a child node for the root
node for each remaining vertex that is
adjacent to the first vertex.
 At each node in level 2, create a child node
for each of the adjacent vertices that are not
in the path from the root to this vertex, and so
on.

39. 39
Example
18
C F
3 15 4 10
12 5 19
A B D H
6 5 4
22
E G

40. 40
Backtracking Algorithms
The tic-tac-toe game
x x
How can a computer play
the game?
Remember Deep Blue?

41. 41
Backtracking Algorithms
The tic-tac-toe game
x
x
0 1 2
0
1
2
(1,1)C
(0,0)H (0,1)H (0,2)H (1,0)H...
(0,0)C, (0,1)C, (1,0)C...
(0,1)H, (1,0)H, …, (2,2)H
(0,1)C, (1,0)C, (1,2)C, (2,0)C...
: Computer
x: Human

42. 42
Backtracking Algorithms
3 missionaries and 2 cannibals want to cross the river
Condition:
1. A boat can take one or two (must include a missionary)
2. At any time, on either bank, the number of missionaries
must not be less than the number of cannibals.

43. 43
Backtracking Search
Essentially a simplified depth-first
algorithm using recursion

44. 44
Backtracking Search
(3 variables)
Assignment = {}

45. 45
Backtracking Search
(3 variables)
Assignment = {(X1,v11)}
X1
v11

46. 46
Backtracking Search
(3 variables)
Assignment = {(X1,v11), (X3,v31)}
X1
v11
v31
X3

47. 47
Backtracking Search
(3 variables)
Assignment = {(X1,v11), (X3,v31)}
X1
v11
v31
X3
X2
Assume that no value of X2
leads to a valid assignment
Then, the search algorithm
backtracks to the previous
variable and tries another value

48. 48
Backtracking Search
(3 variables)
Assignment = {(X1,v11), (X3,v32)}
X1
v11
X3
v32v31
X2

49. 49
Backtracking Search
(3 variables)
Assignment = {(X1,v11), (X3,v32)}
X1
v11
X3
v32
X2
Assume again that no value of
X2 leads to a valid assignment
The search algorithm
backtracks to the previous
variable (X3) and tries
another value. But assume
that X3 has only two
possible values. The
algorithm backtracks to X1
v31
X2

50. 50
Backtracking Search
(3 variables)
Assignment = {(X1,v12)}
X1
v11
X3
v32
X2
v31
X2
v12

51. 51
Backtracking Search
(3 variables)
Assignment = {(X1,v12), (X2,v21)}
X1
v11
X3
v32
X2
v31
X2
v12
v21
X2

52. 52
Backtracking Search
(3 variables)
Assignment = {(X1,v12), (X2,v21)}
X1
v11
X3
v32
X2
v31
X2
v12
v21
X2
The algorithm need not consider
the variables in the same order in
this sub-tree as in the other

53. 53
Backtracking Search
(3 variables)
Assignment = {(X1,v12), (X2,v21), (X3,v32)}
X1
v11
X3
v32
X2
v31
X2
v12
v21
X2
v32
X3

54. 54
Backtracking Search
(3 variables)
Assignment = {(X1,v12), (X2,v21), (X3,v32)}
X1
v11
X3
v32
X2
v31
X2
v12
v21
X2
v32
X3
The algorithm need
not consider the values
of X3 in the same order
in this sub-tree

55. 55
Backtracking Search
(3 variables)
Assignment = {(X1,v12), (X2,v21), (X3,v32)}
X1
v11
X3
v32
X2
v31
X2
v12
v21
X2
v32
X3
Since there are only
three variables, the
assignment is complete

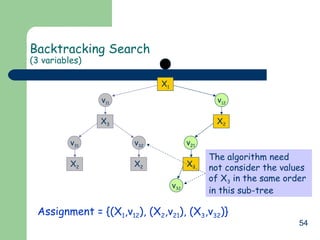
56. 56
Backtracking Algorithm
CSP-BACKTRACKING(A)
1. If assignment A is complete then return A
2. X  select a variable not in A
3. D  select an ordering on the domain of X
4. For each value v in D do
a. Add (Xv) to A
b. If A is valid then
i. result  CSP-BACKTRACKING(A)
ii. If result ≠ failure then return result
5. Return failure
Call CSP-BACKTRACKING({})
[This recursive algorithm keeps too much data in memory.
An iterative version could save memory (left as an exercise)]

57. 57
Map Coloring
{}
WA=red WA=green WA=blue
WA=red
NT=green
WA=red
NT=blue
WA=red
NT=green
Q=red
WA=red
NT=green
Q=blue
WA
NT
SA
Q
NSW
V
T

58. 58
Chapter Summary
 Backtracking is an algorithm design technique
for solving problems in which the number of
choices grows at least exponentially with their
instant size.
 This approach makes it possible to solve many
large instances of NP-hard problems in an
acceptable amount of time.
 The technique constructs a pruned state space
tree.
 Backtracking constructs its state-space tree in
the depth-first search fashion in the majority
of its applications.