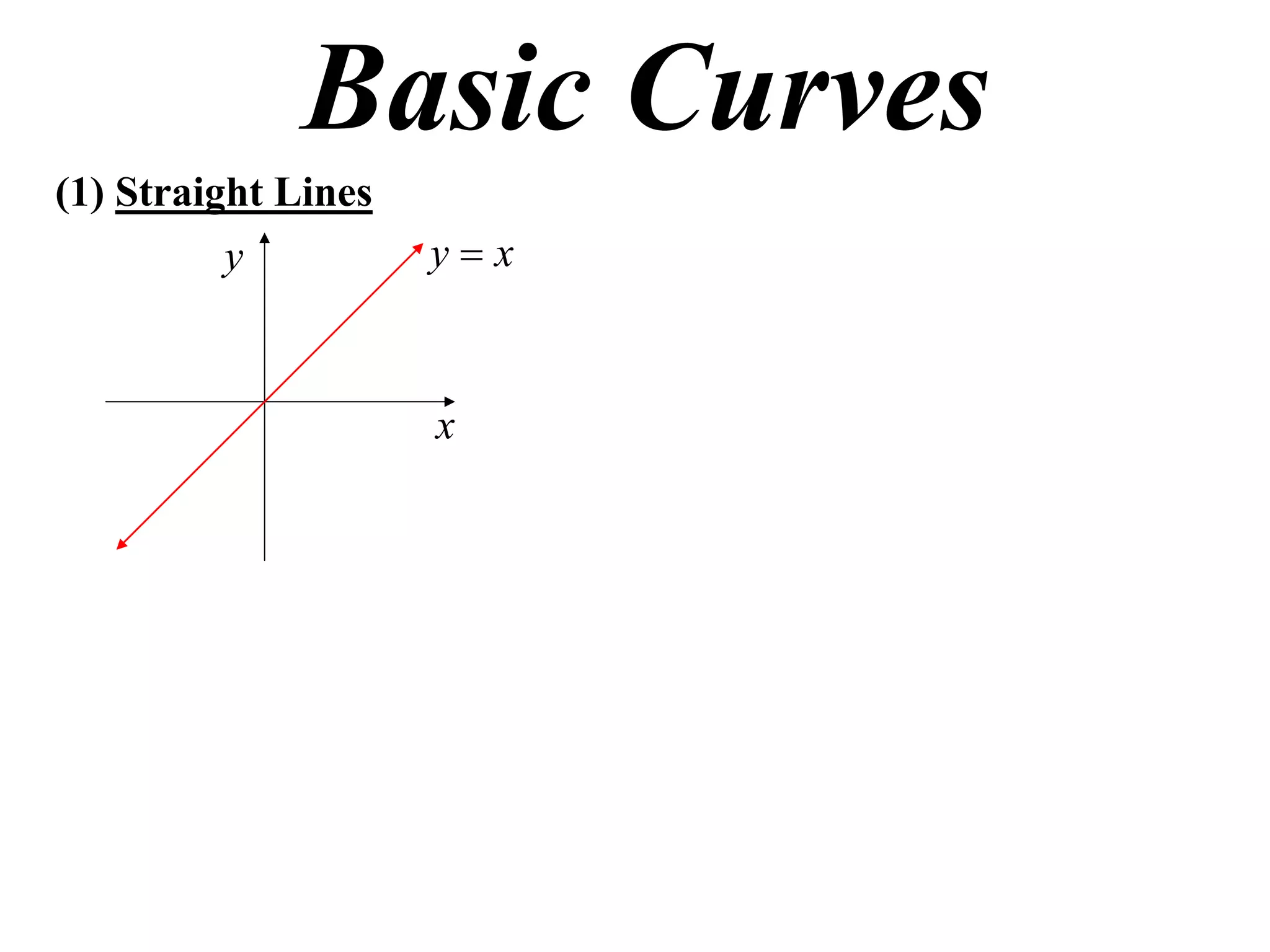
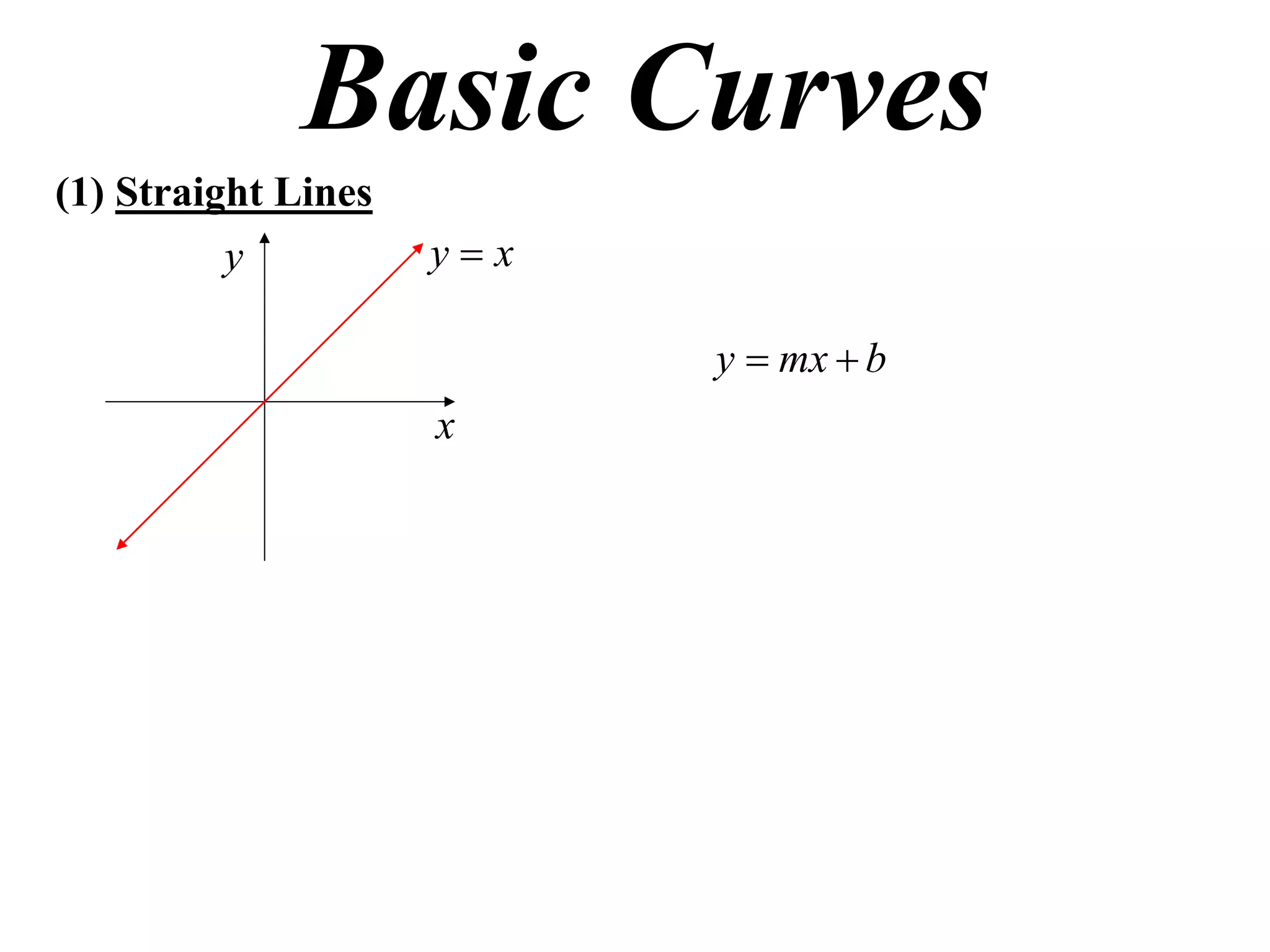
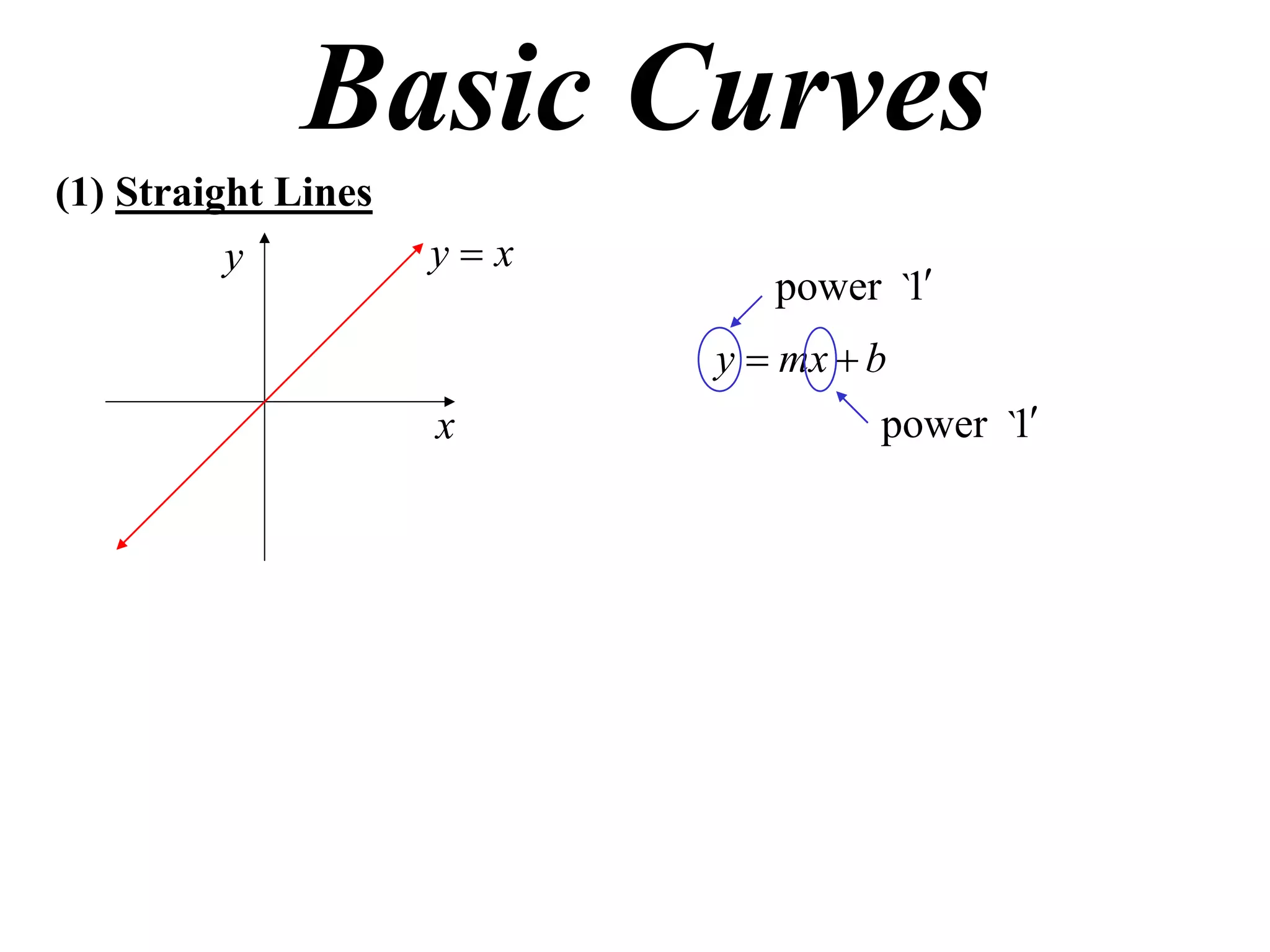
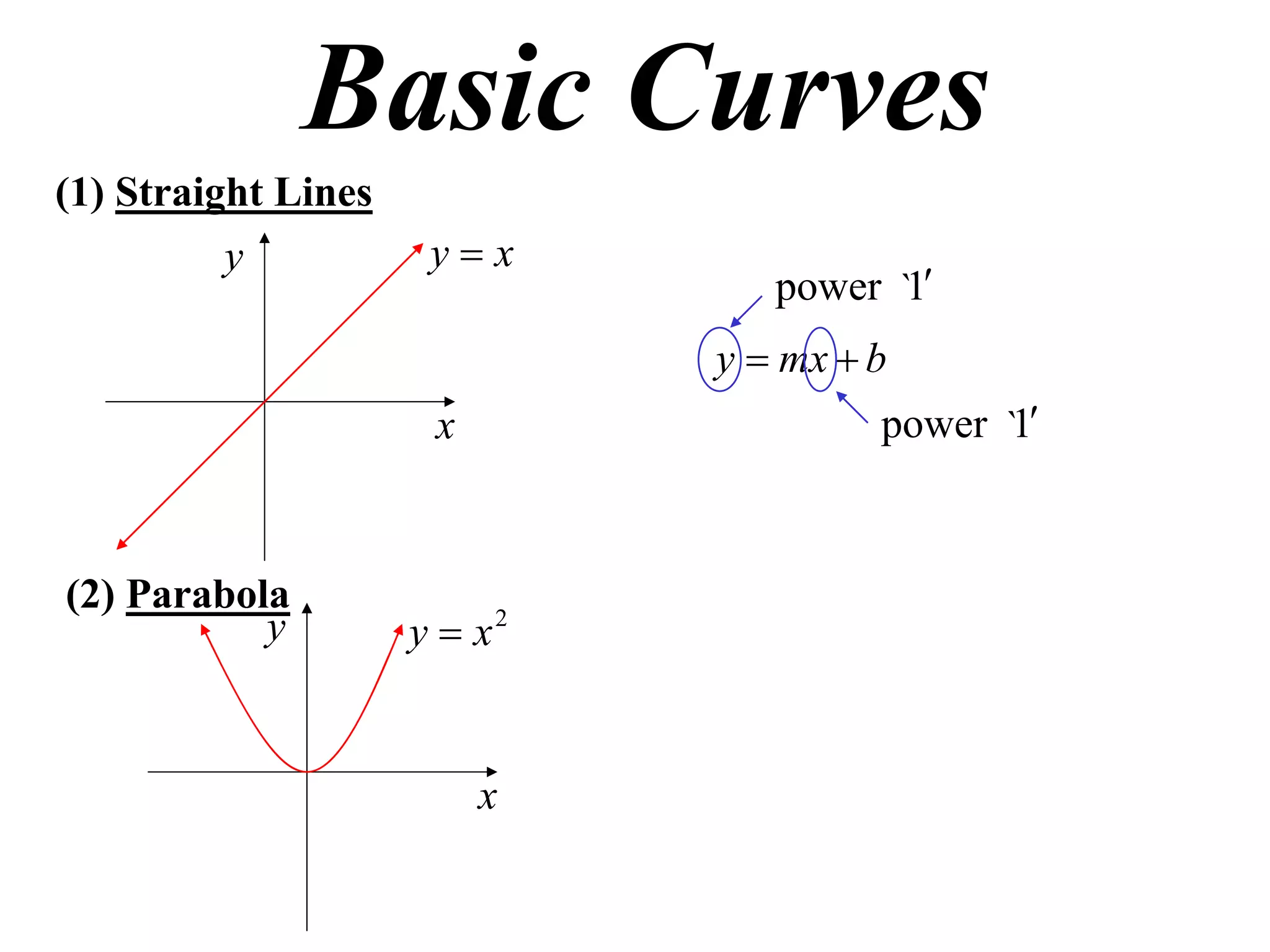
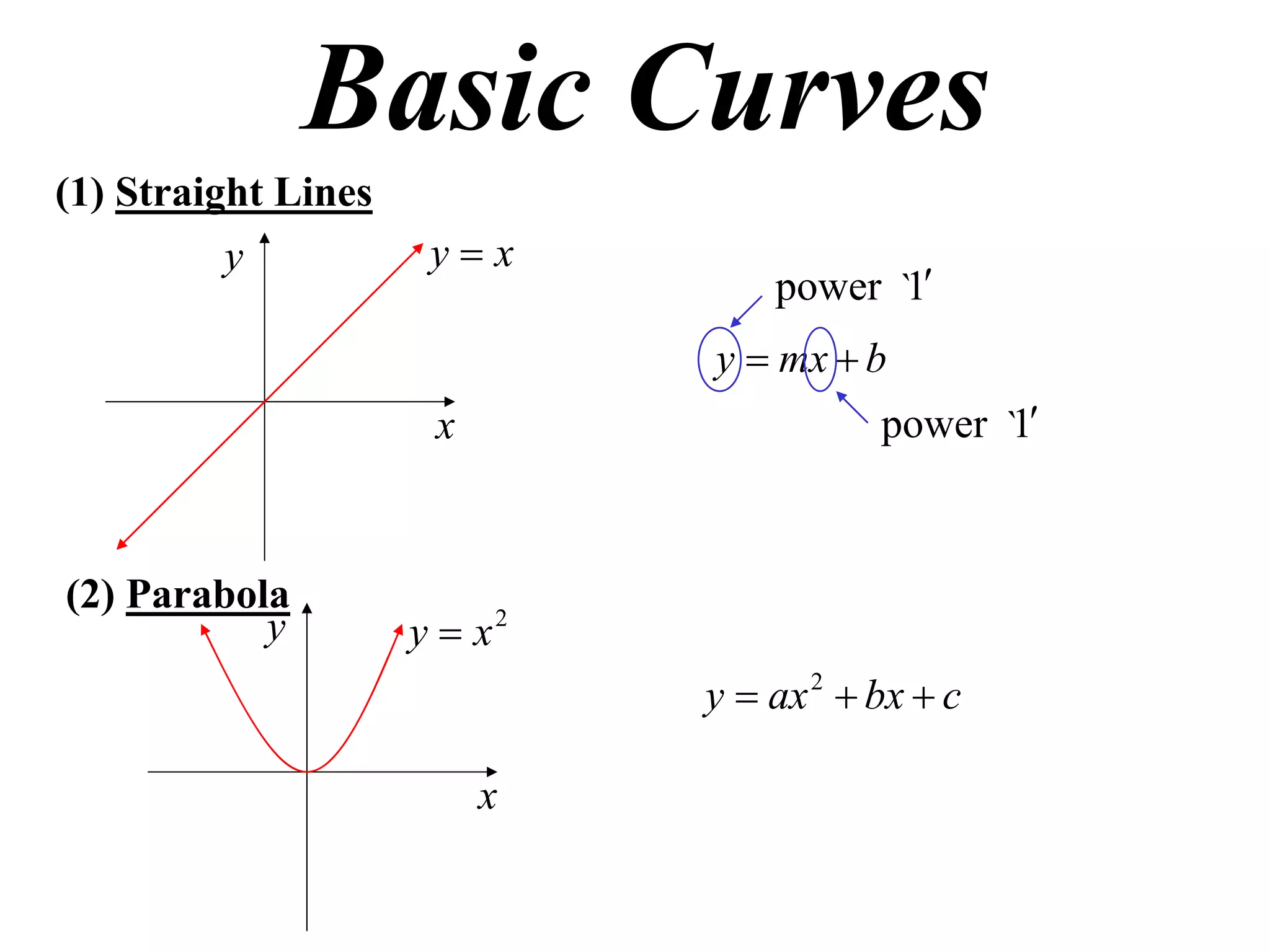
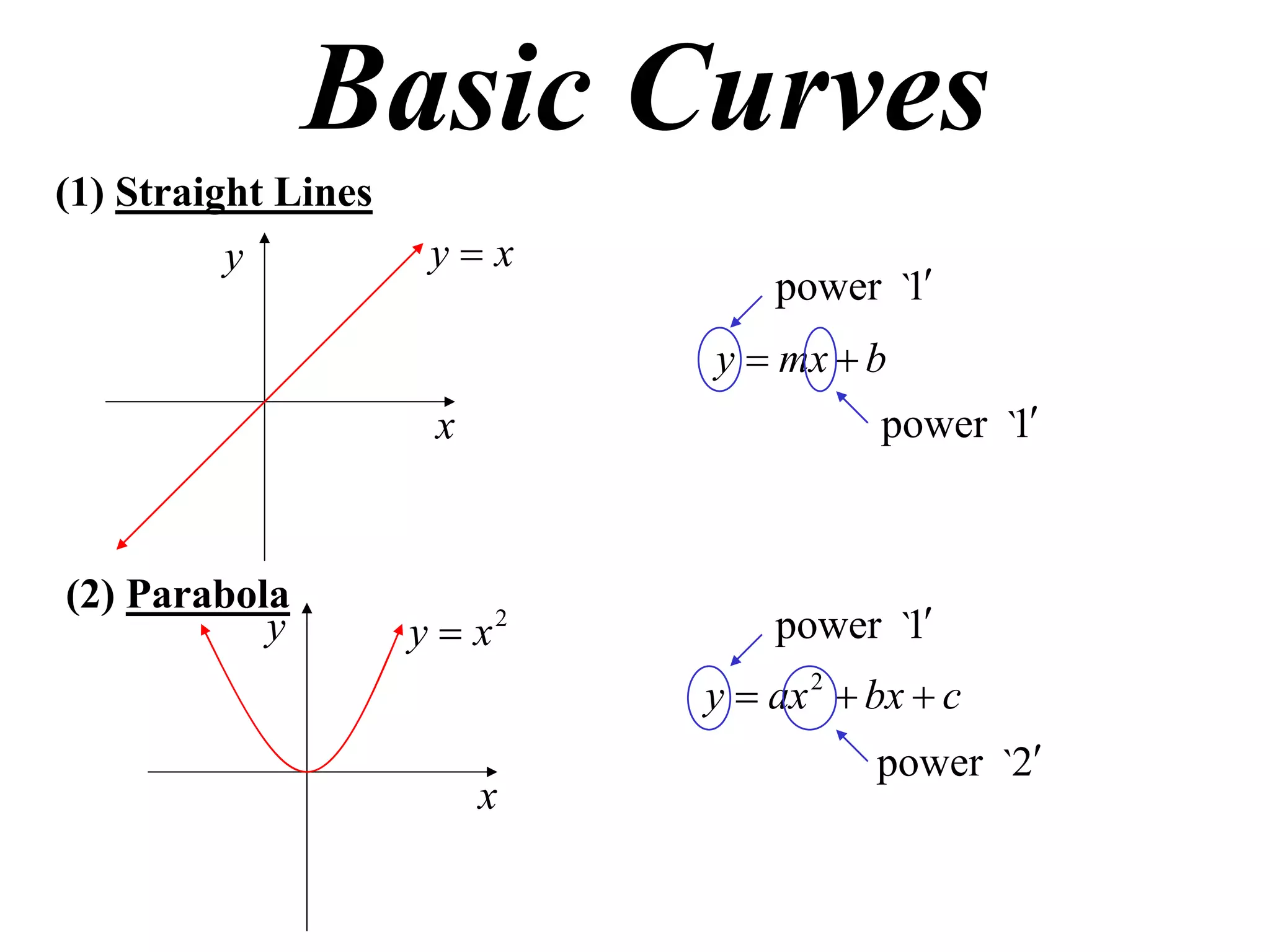
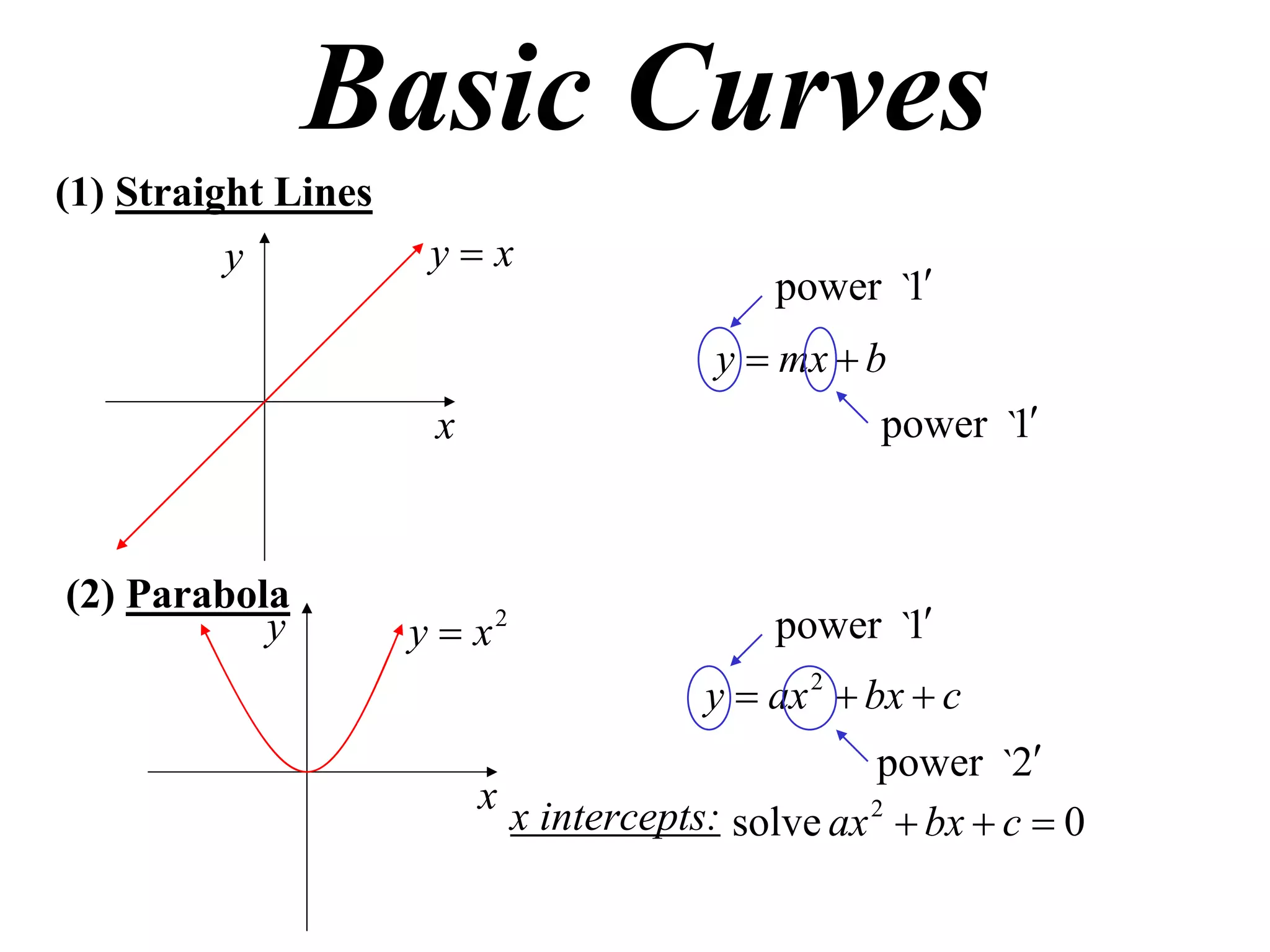
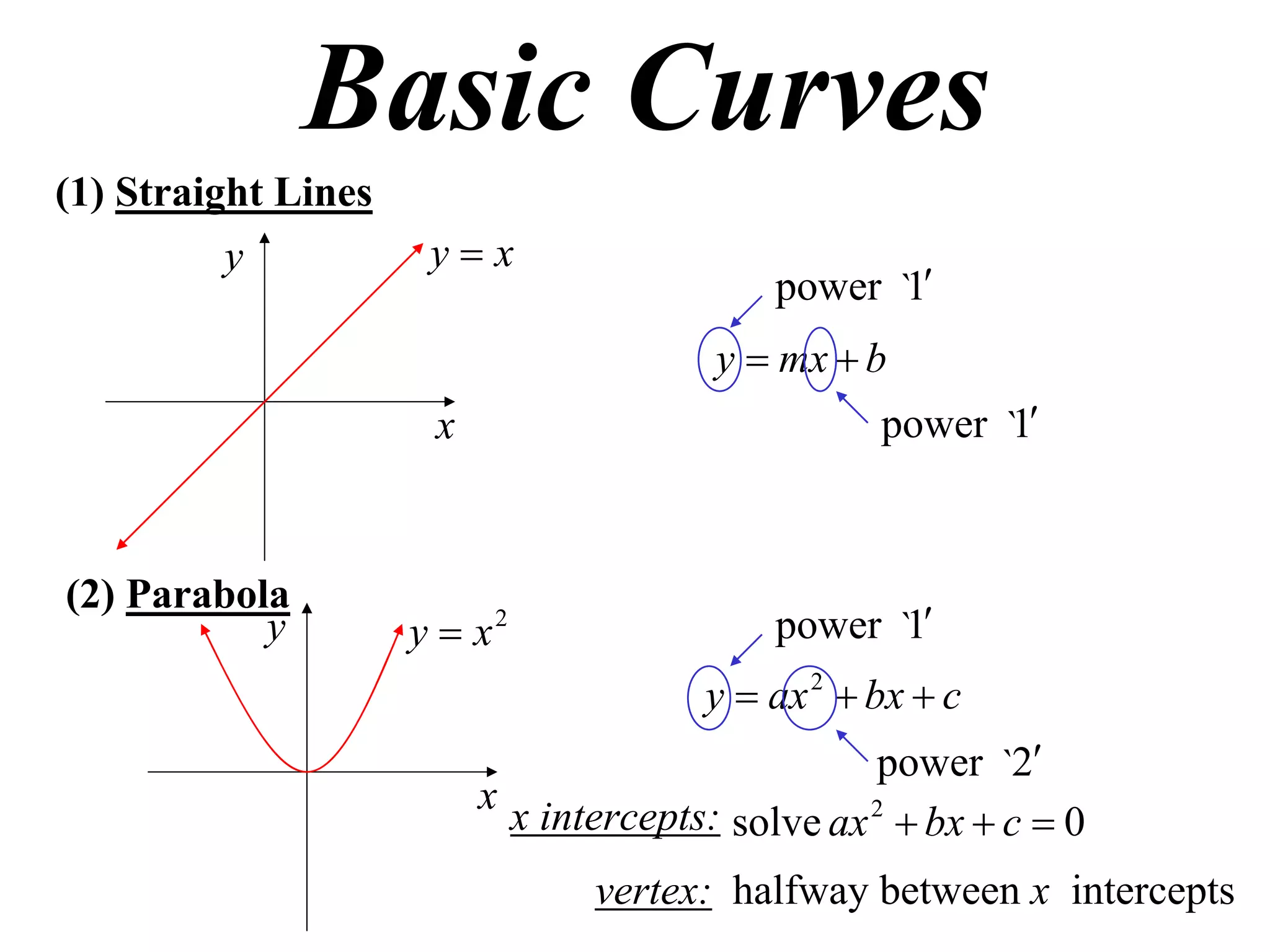
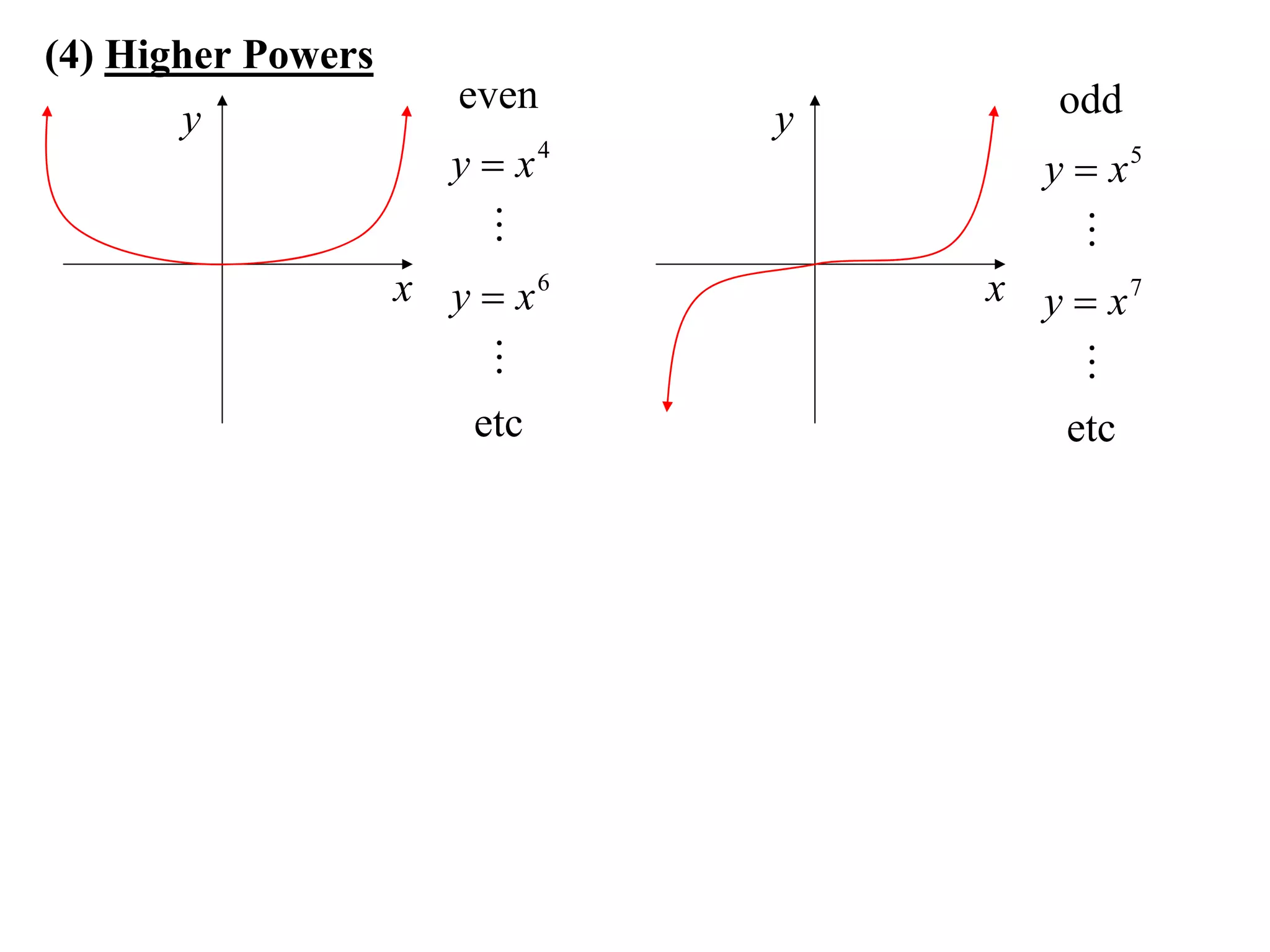
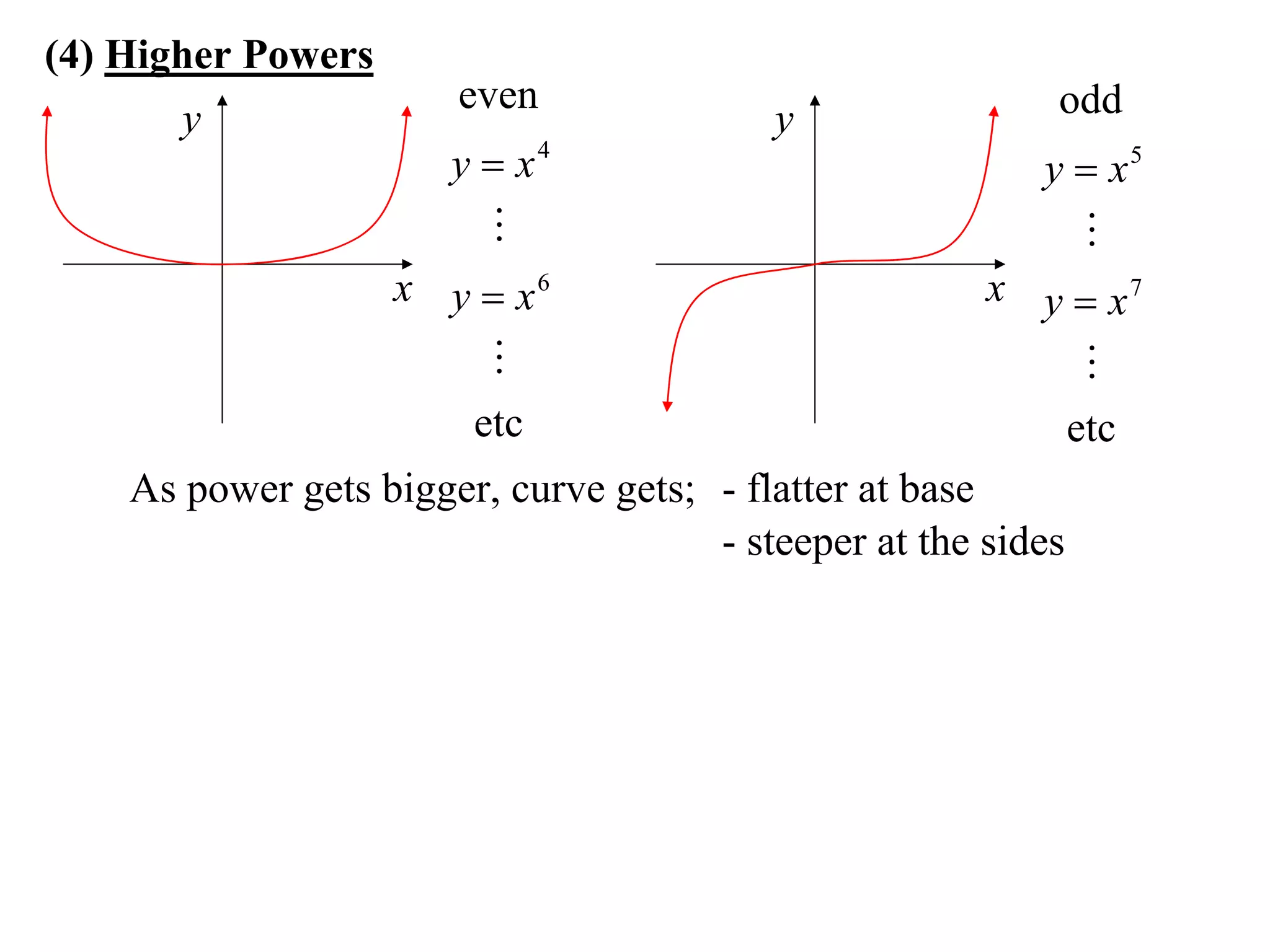
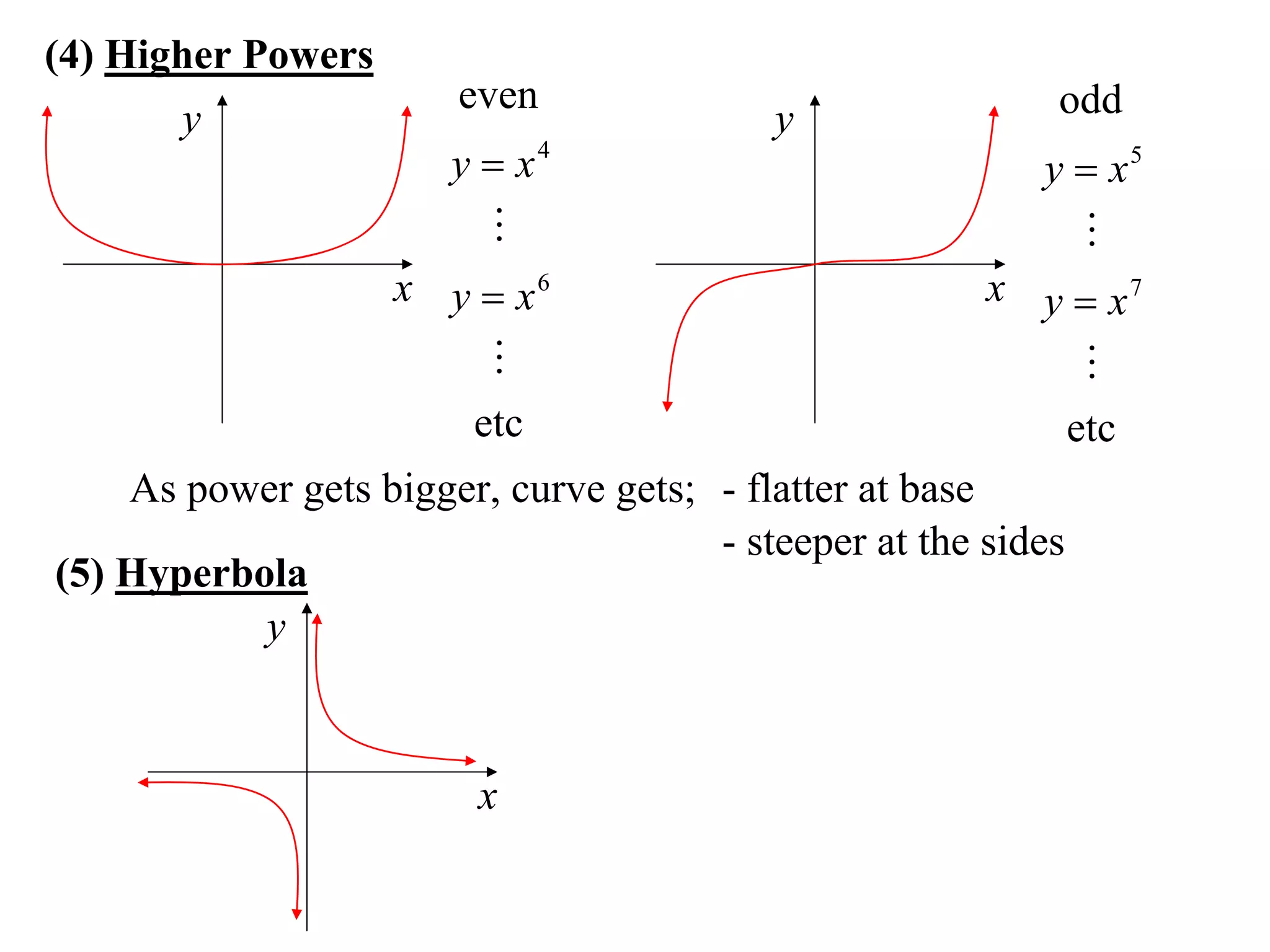
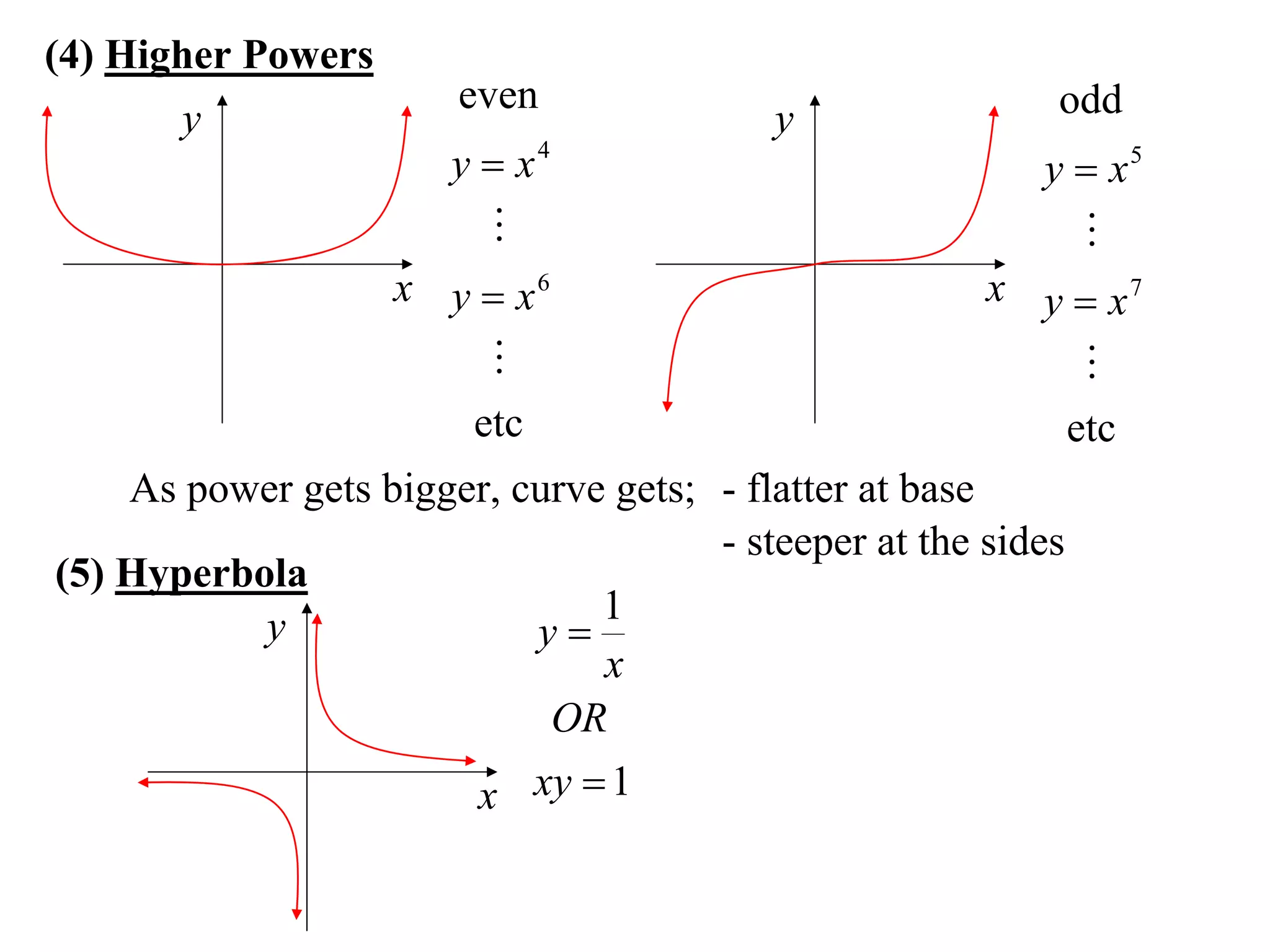
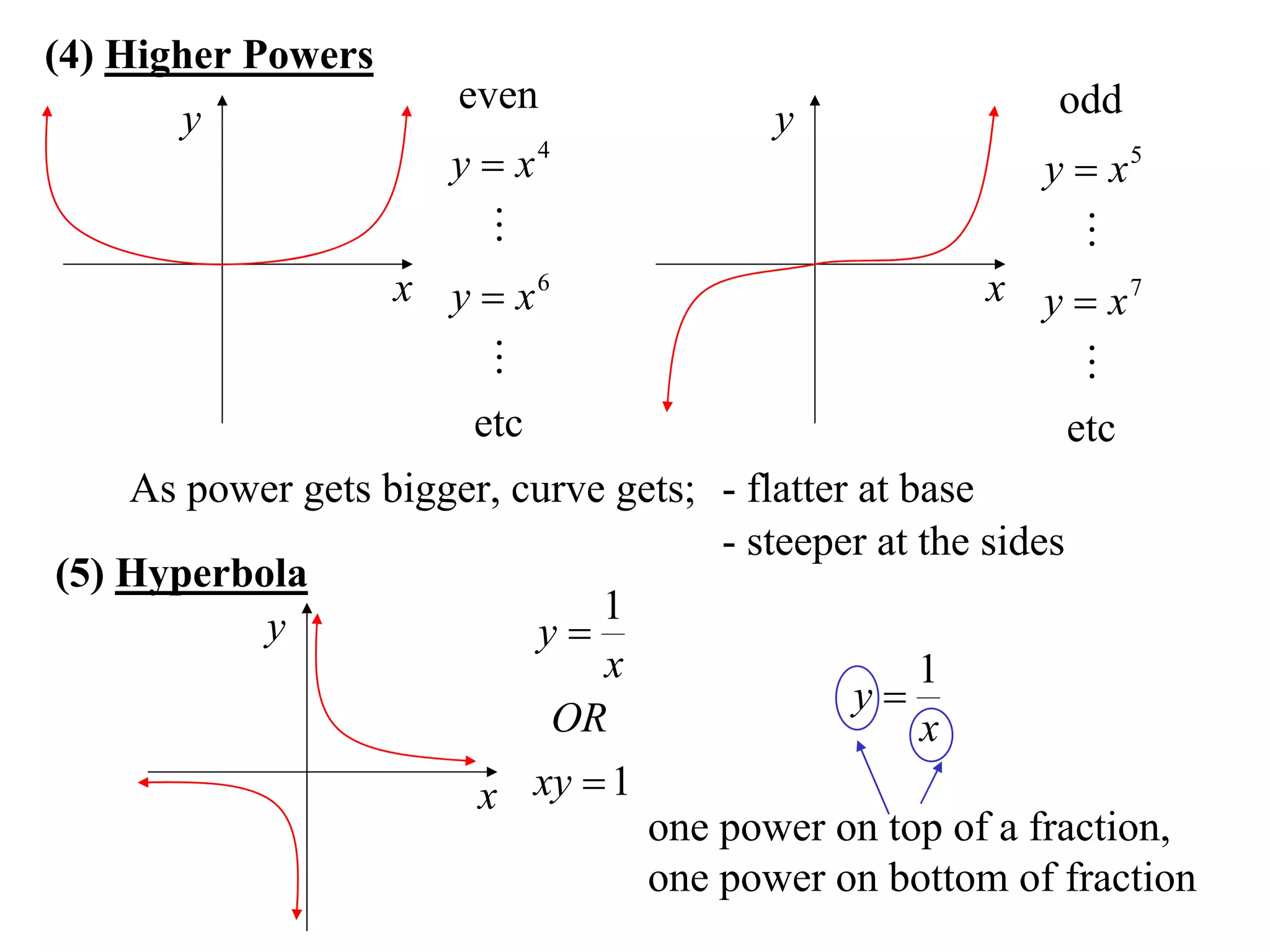
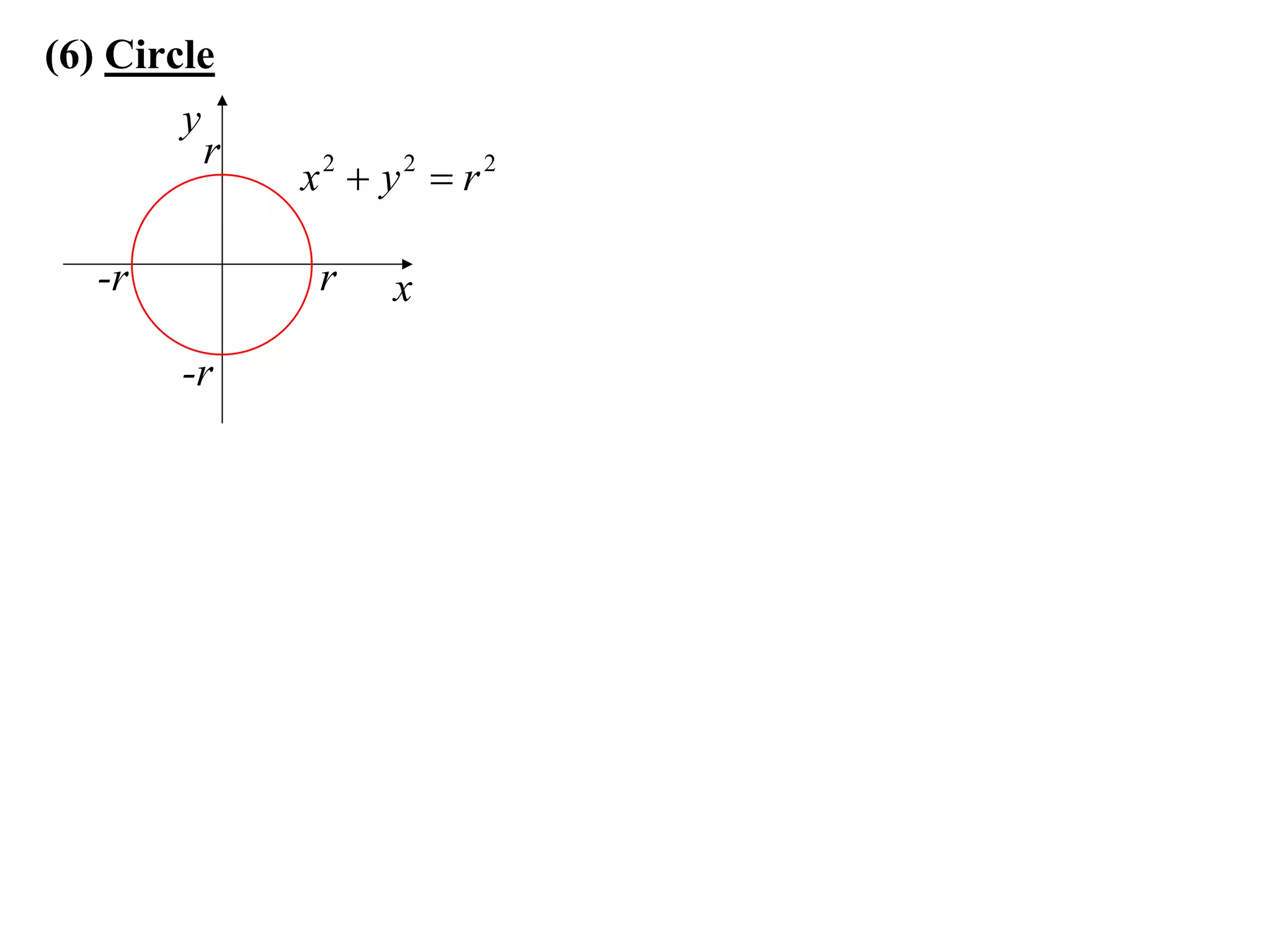
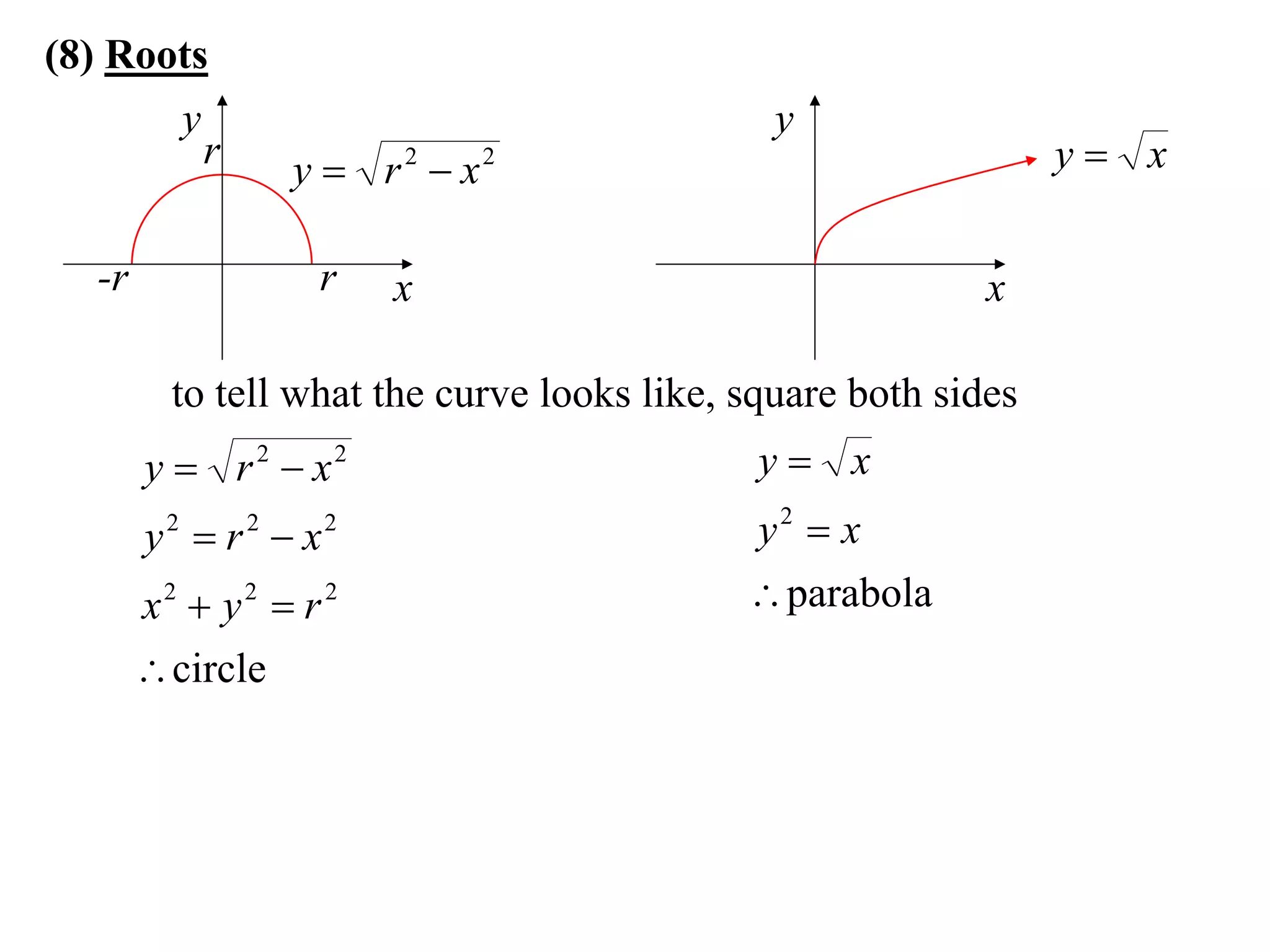
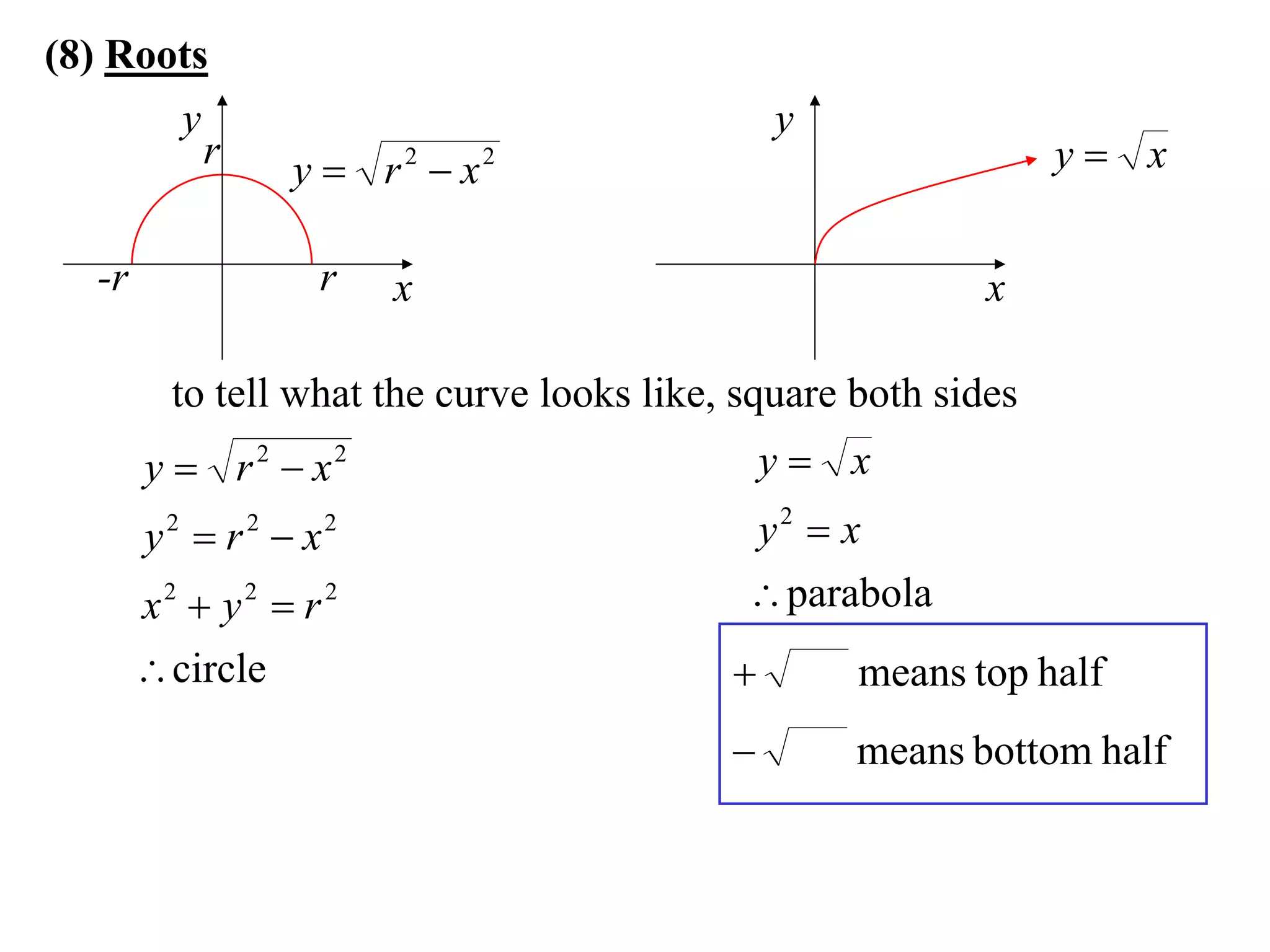
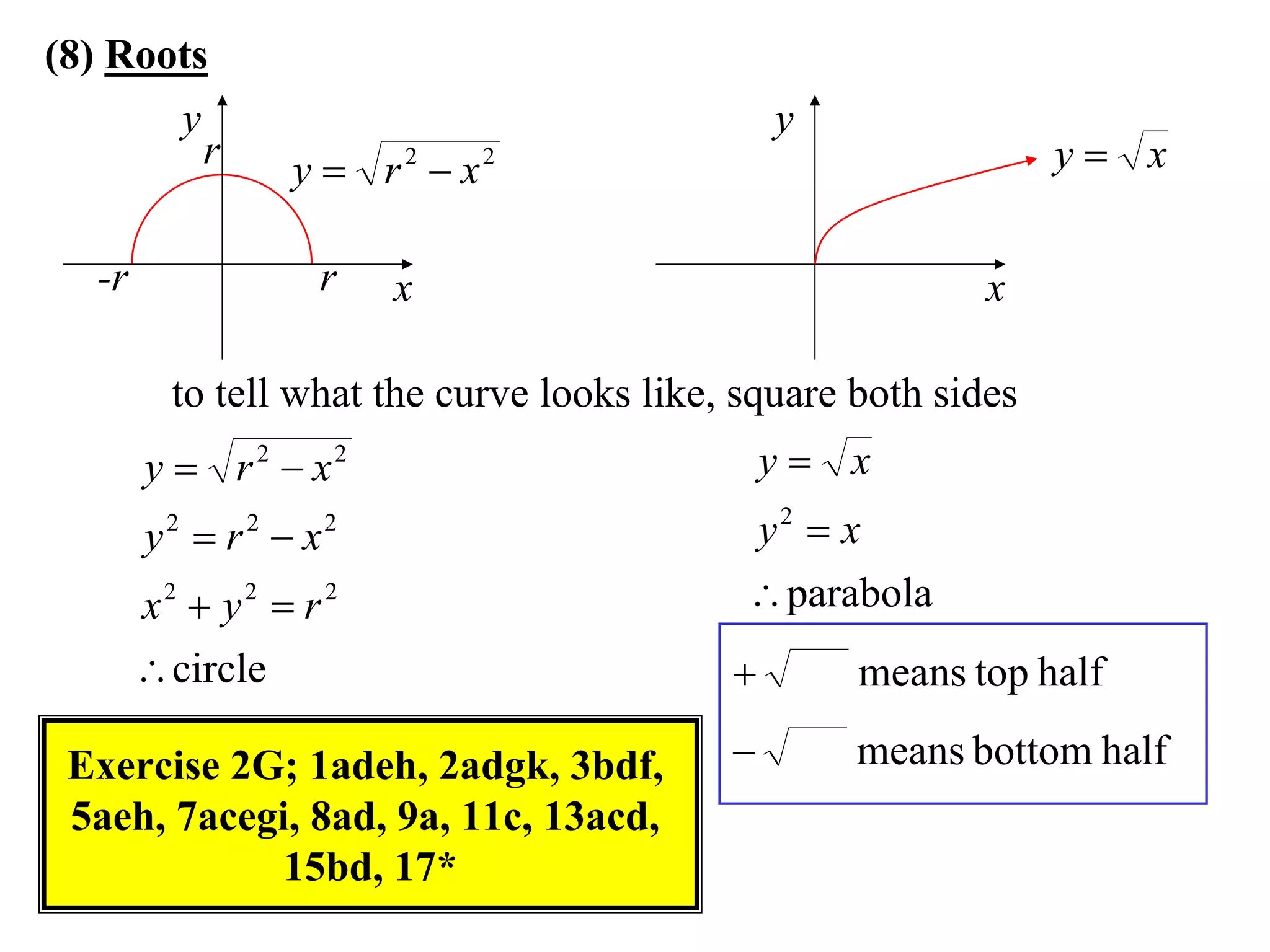
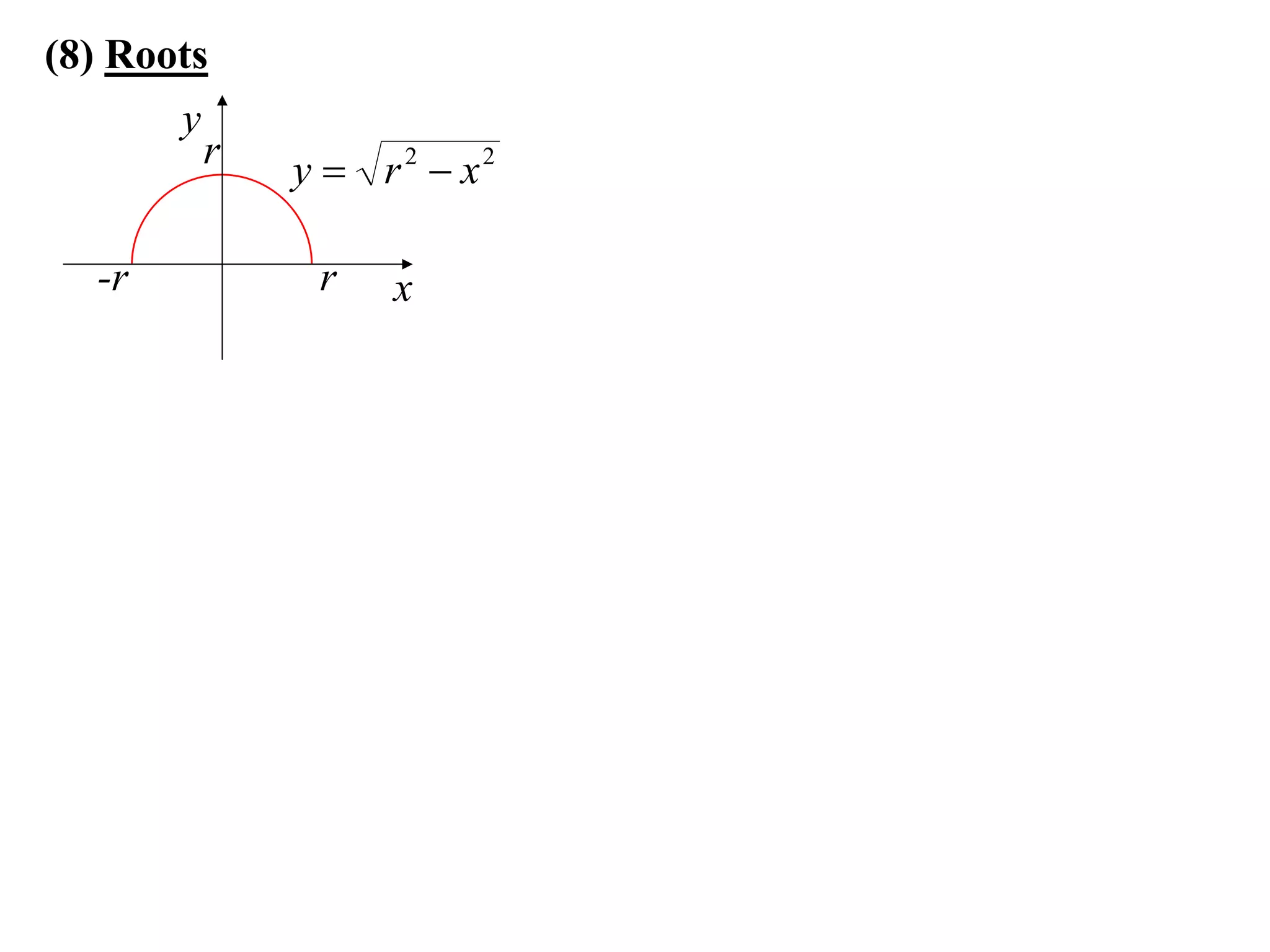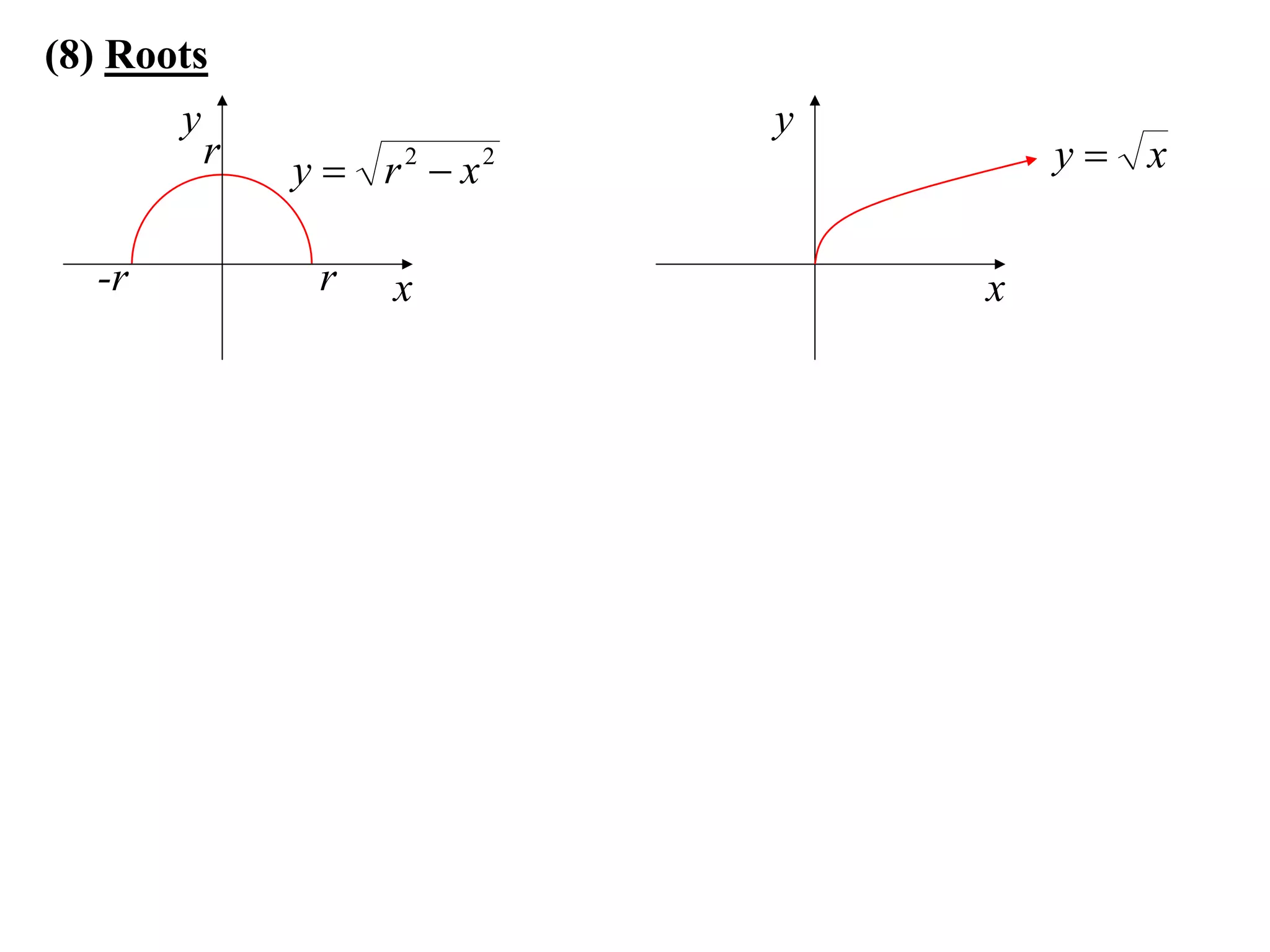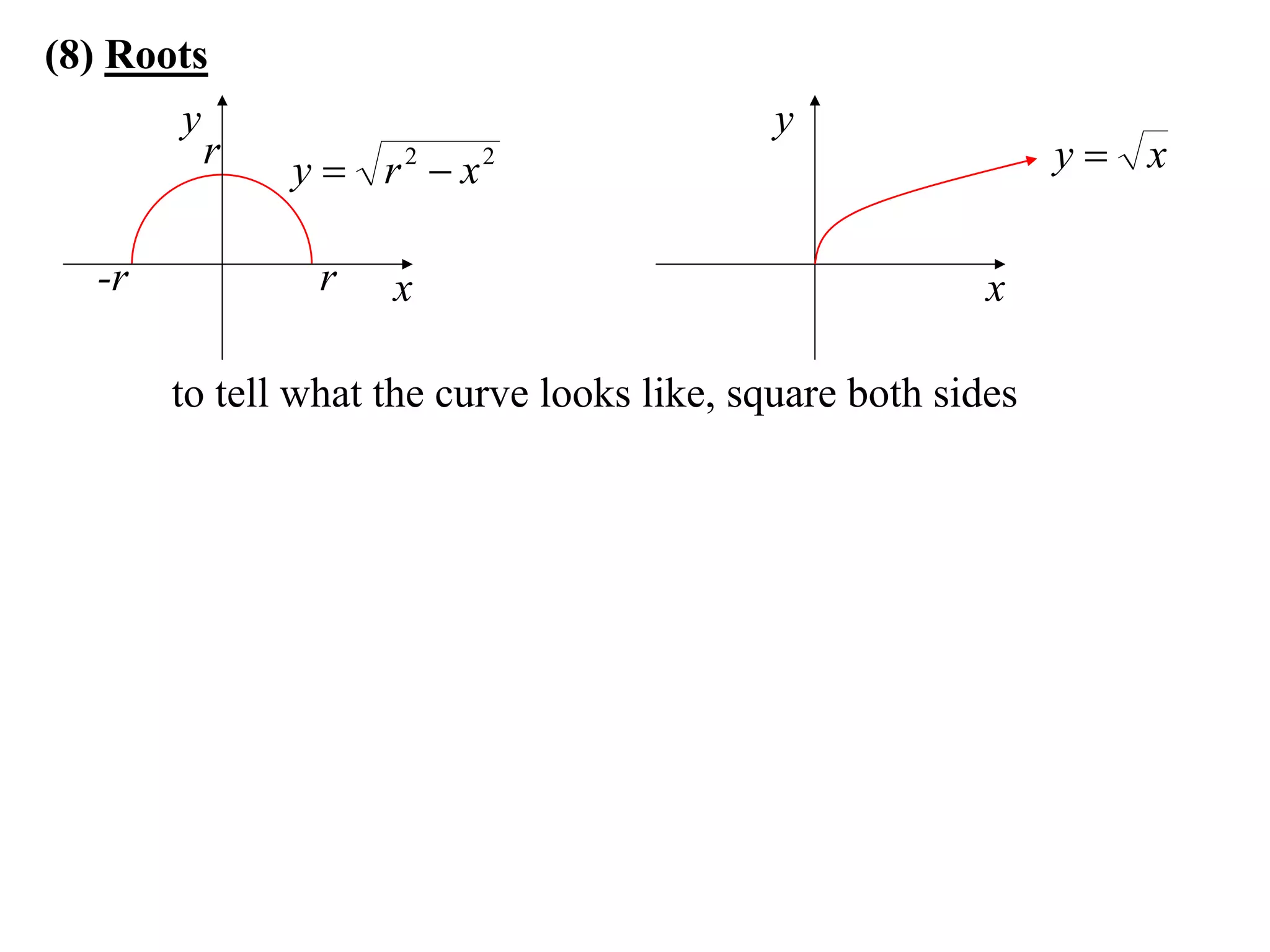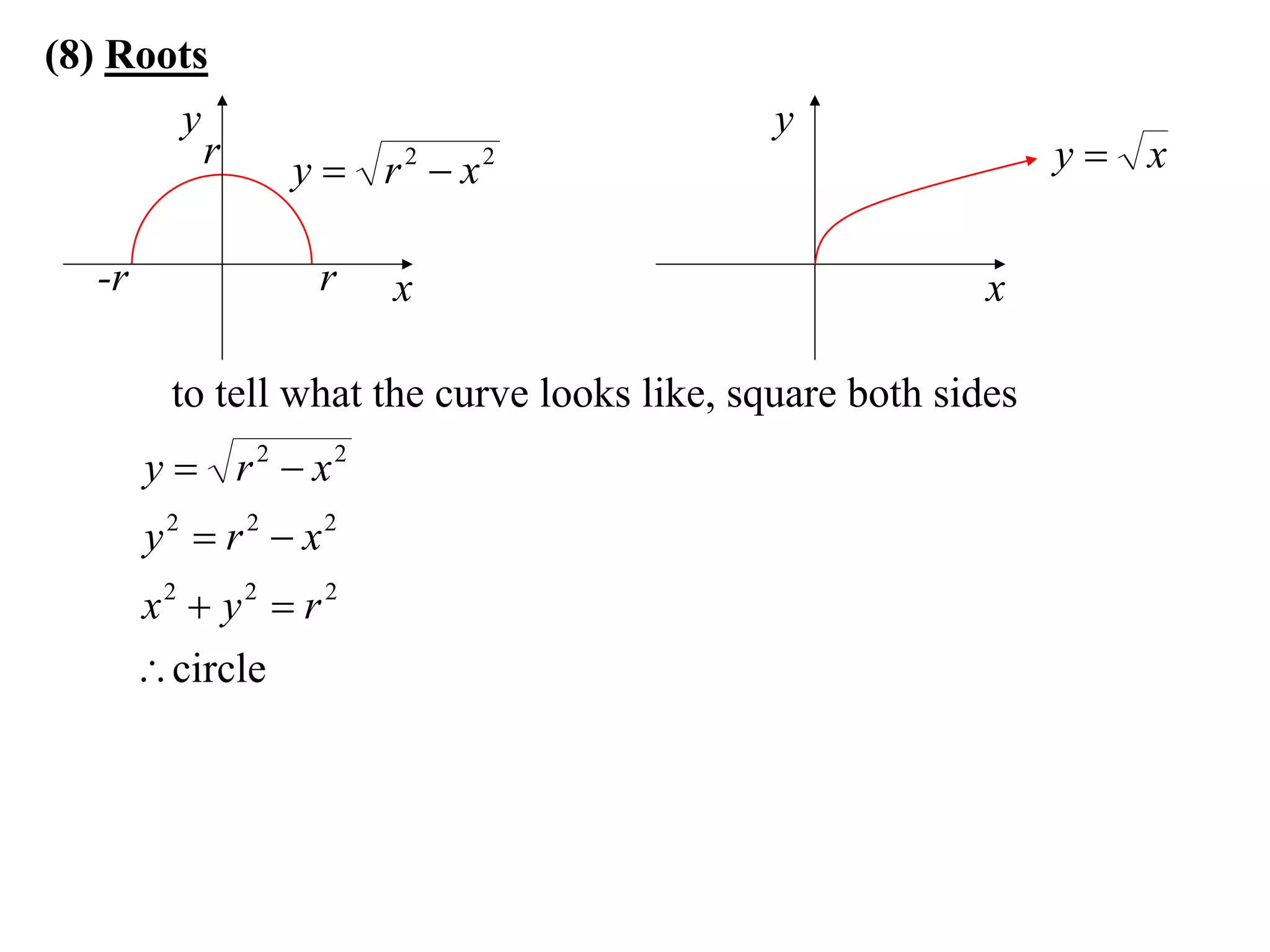The document provides information on sketching graphs of basic curves. It lists 8 types of basic curves: (1) straight lines, (2) parabolas, (3) cubics, (4) higher powers, (5) hyperbolas, (6) circles, (7) exponentials, and (8) roots. For each type of curve, it gives the standard form of the equation and notes on identifying features like intercepts, vertices, and the overall shape of the graph. Sketching curves involves finding intercepts and using a table of values to plot points if needed.

1. Sketching Graphs

2. Sketching Graphs
* Numbers on axes must be evenly spaced

3. Sketching Graphs
* Numbers on axes must be evenly spaced
* y intercept occurs when x = 0

4. Sketching Graphs
* Numbers on axes must be evenly spaced
* y intercept occurs when x = 0
* x intercept occurs when y = 0

5. Sketching Graphs
* Numbers on axes must be evenly spaced
* y intercept occurs when x = 0
* x intercept occurs when y = 0
Once the intercepts have been found, curves are easy to
sketch, if you know the basic shape.

6. Sketching Graphs
* Numbers on axes must be evenly spaced
* y intercept occurs when x = 0
* x intercept occurs when y = 0
Once the intercepts have been found, curves are easy to
sketch, if you know the basic shape.
If in doubt use a table of values and plot some points

7. Basic Curves

8. Basic Curves
(1) Straight Lines
y yx
x

9. Basic Curves
(1) Straight Lines
y yx
y  mx  b
x

10. Basic Curves
(1) Straight Lines
y yx
power `1
y  mx  b
x power `1

11. Basic Curves
(1) Straight Lines
y yx
power `1
y  mx  b
x power `1
(2) Parabola
y y  x2
x

12. Basic Curves
(1) Straight Lines
y yx
power `1
y  mx  b
x power `1
(2) Parabola
y y  x2
y  ax 2  bx  c
x

13. Basic Curves
(1) Straight Lines
y yx
power `1
y  mx  b
x power `1
(2) Parabola
y y  x2 power `1
y  ax 2  bx  c
power `2
x

14. Basic Curves
(1) Straight Lines
y yx
power `1
y  mx  b
x power `1
(2) Parabola
y y  x2 power `1
y  ax 2  bx  c
power `2
x x intercepts:
solve ax 2  bx  c  0

15. Basic Curves
(1) Straight Lines
y yx
power `1
y  mx  b
x power `1
(2) Parabola
y y  x2 power `1
y  ax 2  bx  c
power `2
x x intercepts:
solve ax 2  bx  c  0
vertex: halfway between x intercepts

16. e.g. find the x intercepts and vertex of y  x 2  4 x  3

17. e.g. find the x intercepts and vertex of y  x 2  4 x  3
y   x  2  1
2
 vertex 2,1

18. e.g. find the x intercepts and vertex of y  x 2  4 x  3
y   x  2   1 x intercepts:  x  2 2  1
2
 vertex 2,1

19. e.g. find the x intercepts and vertex of y  x 2  4 x  3
y   x  2   1 x intercepts:  x  2 2  1
2
 vertex 2,1 x  2  1
x  2 1
x = 1 or x = 3

20. e.g. find the x intercepts and vertex of y  x 2  4 x  3
y   x  2   1 x intercepts:  x  2 2  1
2
 vertex 2,1 x  2  1
x  2 1
y x = 1 or x = 3
1 3 x
2,1

21. e.g. find the x intercepts and vertex of y  x 2  4 x  3
y   x  2   1 x intercepts:  x  2 2  1
2
 vertex 2,1 x  2  1
x  2 1
y x = 1 or x = 3
1 3 x
2,1
(3) Cubic
y y  x3
x

22. e.g. find the x intercepts and vertex of y  x 2  4 x  3
y   x  2   1 x intercepts:  x  2 2  1
2
 vertex 2,1 x  2  1
x  2 1
y x = 1 or x = 3
1 3 x
2,1
(3) Cubic
y y  x3
y  ax 3  bx 2  cx  d
x

23. e.g. find the x intercepts and vertex of y  x 2  4 x  3
y   x  2   1 x intercepts:  x  2 2  1
2
 vertex 2,1 x  2  1
x  2 1
y x = 1 or x = 3
1 3 x
2,1
(3) Cubic
y  x3 power `1
y
y  ax 3  bx 2  cx  d
x power `3

24. e.g. find the x intercepts and vertex of y  x 2  4 x  3
y   x  2   1 x intercepts:  x  2 2  1
2
 vertex 2,1 x  2  1
x  2 1
y x = 1 or x = 3
1 3 x
2,1
(3) Cubic
y  x3 power `1
y
y  ax 3  bx 2  cx  d
x power `3
If it can be factorised to y  a x  k 
3
then it will look like the basic cubic.

25. e.g. find the x intercepts and vertex of y  x 2  4 x  3
y   x  2   1 x intercepts:  x  2 2  1
2
 vertex 2,1 x  2  1
x  2 1
y x = 1 or x = 3
1 3 x
2,1
(3) Cubic
y  x3 power `1
y
y  ax 3  bx 2  cx  d Otherwise;
y
x power `3
If it can be factorised to y  a x  k 
3
x
then it will look like the basic cubic.

26. (4) Higher Powers
even
y
y  x4

x y  x6

etc

27. (4) Higher Powers
even odd
y y
y  x4 y  x5
 
x y  x6 x y  x7
 
etc etc

28. (4) Higher Powers
even odd
y y
y  x4 y  x5
 
x y  x6 x y  x7
 
etc etc
As power gets bigger, curve gets; - flatter at base
- steeper at the sides

29. (4) Higher Powers
even odd
y y
y  x4 y  x5
 
x y  x6 x y  x7
 
etc etc
As power gets bigger, curve gets; - flatter at base
- steeper at the sides
(5) Hyperbola
y
x

30. (4) Higher Powers
even odd
y y
y  x4 y  x5
 
x y  x6 x y  x7
 
etc etc
As power gets bigger, curve gets; - flatter at base
- steeper at the sides
(5) Hyperbola
1
y y
x
OR
x xy  1

31. (4) Higher Powers
even odd
y y
y  x4 y  x5
 
x y  x6 x y  x7
 
etc etc
As power gets bigger, curve gets; - flatter at base
- steeper at the sides
(5) Hyperbola
1
y y
x 1
y
OR x
x xy  1
one power on top of a fraction,
one power on bottom of fraction

32. (6) Circle
y
r
x2  y2  r 2
-r r x
-r

33. (6) Circle
y
r
x2  y2  r 2
x2  y2  r 2
-r r x
both power ‘2’
-r coefficients are the same

34. (6) Circle
y
r
x2  y2  r 2
x2  y2  r 2
-r r x
both power ‘2’
-r coefficients are the same
(7) Exponential
y y  ax
a  1
1
x

35. (6) Circle
y
r
x2  y2  r 2
x2  y2  r 2
-r r x
both power ‘2’
-r coefficients are the same
(7) Exponential
y y  ax
a  1
1 y  ax
x pronumeral in the power

36. (8) Roots
y
r y  r 2  x2
-r r x

37. (8) Roots
y y
r y  r 2  x2 y x
-r r x x

38. (8) Roots
y y
r y  r 2  x2 y x
-r r x x
to tell what the curve looks like, square both sides

39. (8) Roots
y y
r y  r 2  x2 y x
-r r x x
to tell what the curve looks like, square both sides
y  r 2  x2
y2  r 2  x2
x2  y2  r 2
 circle

40. (8) Roots
y y
r y  r 2  x2 y x
-r r x x
to tell what the curve looks like, square both sides
y  r 2  x2 y x
y2  r 2  x2 y2  x
x2  y2  r 2  parabola
 circle

41. (8) Roots
y y
r y  r 2  x2 y x
-r r x x
to tell what the curve looks like, square both sides
y  r 2  x2 y x
y2  r 2  x2 y2  x
x2  y2  r 2  parabola
 circle  means top half
 means bottom half

42. (8) Roots
y y
r y  r 2  x2 y x
-r r x x
to tell what the curve looks like, square both sides
y  r 2  x2 y x
y2  r 2  x2 y2  x
x2  y2  r 2  parabola
 circle  means top half
Exercise 2G; 1adeh, 2adgk, 3bdf,  means bottom half
5aeh, 7acegi, 8ad, 9a, 11c, 13acd,
15bd, 17*