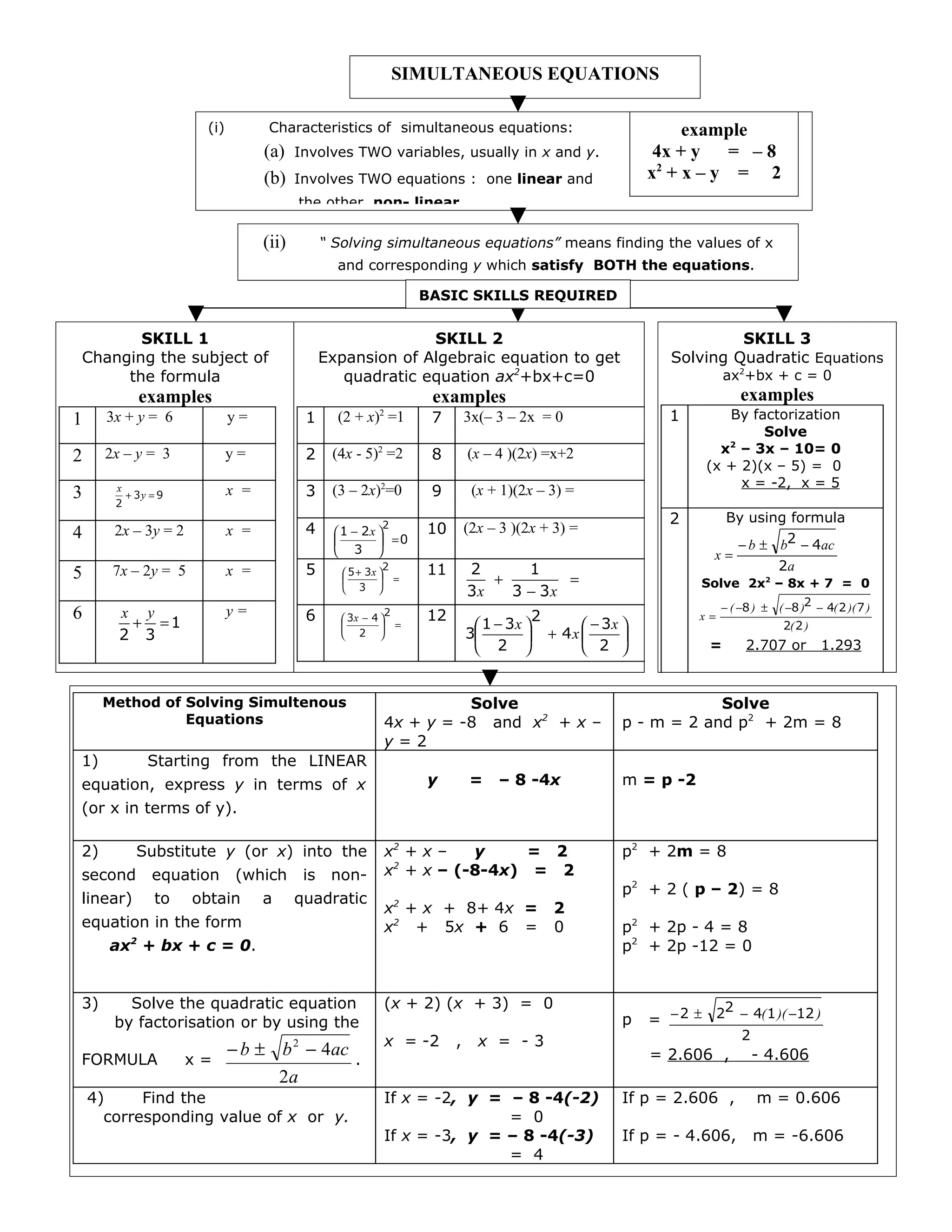
1) Simultaneous equations involve two variables in two equations that are solved simultaneously to find the values of the variables. 2) To solve simultaneous equations, one first expresses one variable in terms of the other by changing the subject of one linear equation, then substitutes this into the other equation to obtain a quadratic equation. 3) This quadratic equation is then solved using factorisation or the quadratic formula to find the values of the variables that satisfy both original equations.

1. SIMULTANEOUS EQUATIONS
(i) Characteristics of simultaneous equations: example
(a) Involves TWO variables, usually in x and y. 4x + y = –8
(b) Involves TWO equations : one linear and x2 + x – y = 2
the other non- linear.
(ii) “ Solving simultaneous equations” means finding the values of x
and corresponding y which satisfy BOTH the equations.
BASIC SKILLS REQUIRED
SKILL 1 SKILL 2 SKILL 3
Changing the subject of Expansion of Algebraic equation to get Solving Quadratic Equations
the formula quadratic equation ax2+bx+c=0 ax2+bx + c = 0
examples examples examples
1 3x + y = 6 y= 1 (2 + x)2 =1 7 3x(– 3 – 2x = 0 1 By factorization
Solve
2x – y = 3 y= 2 (4x - 5)2 =2 8 (x – 4 )(2x) =x+2 x2 – 3x – 10= 0
2 (x + 2)(x – 5) = 0
x = -2, x = 5
3 x
+ 3y = 9 x = 3 (3 – 2x)2=0 9 (x + 1)(2x – 3) =
2
2 2 By using formula
4 2x – 3y = 2 x = 4  1 − 2x  10 (2x – 3 )(2x + 3) =

 3 
 =0 − b ± b2 − 4ac
x=
7x – 2y = 5 x = 5 2 11 2 1 2a
5  5 + 3x 
  = + = Solve 2x2 – 8x + 7 = 0
3 
 3x 3 − 3x
y= − ( −8 ) ± ( −8 )2 − 4( 2 )( 7 )
6 x y
+ =1 6  3x − 4 
2 12 2 x=
  =  1 − 3x   − 3x  2( 2 )
2 3  2  3  + 4x  
 2   2  = 2.707 or 1.293
Method of Solving Simultenous Solve Solve
Equations 4x + y = -8 and x2 + x – p - m = 2 and p2 + 2m = 8
y=2
1) Starting from the LINEAR
equation, express y in terms of x y = – 8 -4x m = p -2
(or x in terms of y).
2) Substitute y (or x) into the x2 + x – y = 2 p2 + 2m = 8
second equation (which is non- x2 + x – (-8-4x) = 2
p2 + 2 ( p – 2) = 8
linear) to obtain a quadratic 2
x + x + 8+ 4x = 2
equation in the form x2 + 5x + 6 = 0 p2 + 2p - 4 = 8
2
ax + bx + c = 0. p2 + 2p -12 = 0
3) Solve the quadratic equation (x + 2) (x + 3) = 0 2
by factorisation or by using the p = − 2 ± 2 − 4( 1 )( −12 )
x = -2 , x = -3 2
− b ± b 2 − 4ac = 2.606 , - 4.606
FORMULA x= .
2a
4) Find the If x = -2, y = – 8 -4(-2) If p = 2.606 , m = 0.606
corresponding value of x or y. = 0
If x = -3, y = – 8 -4(-3) If p = - 4.606, m = -6.606
= 4