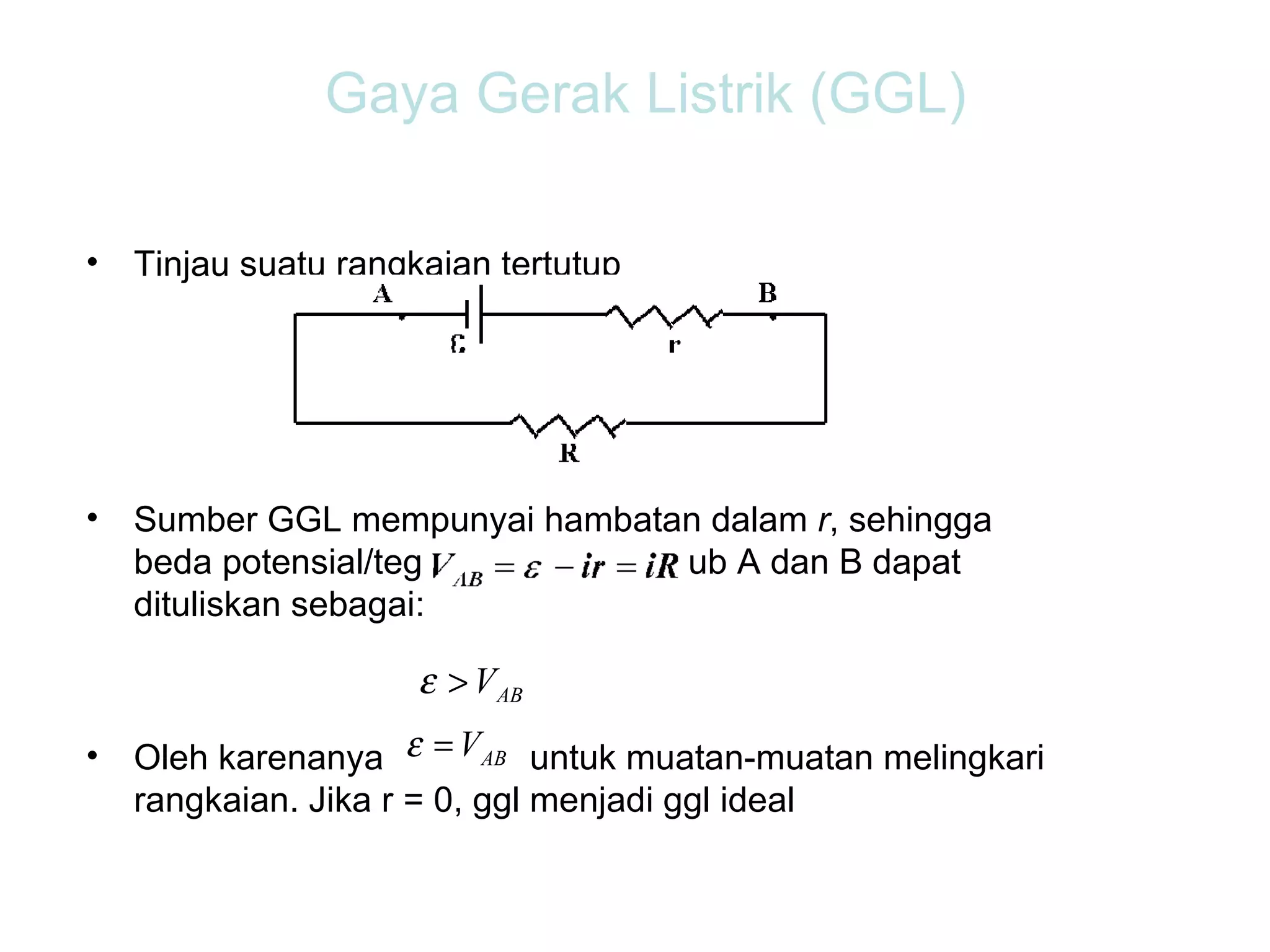
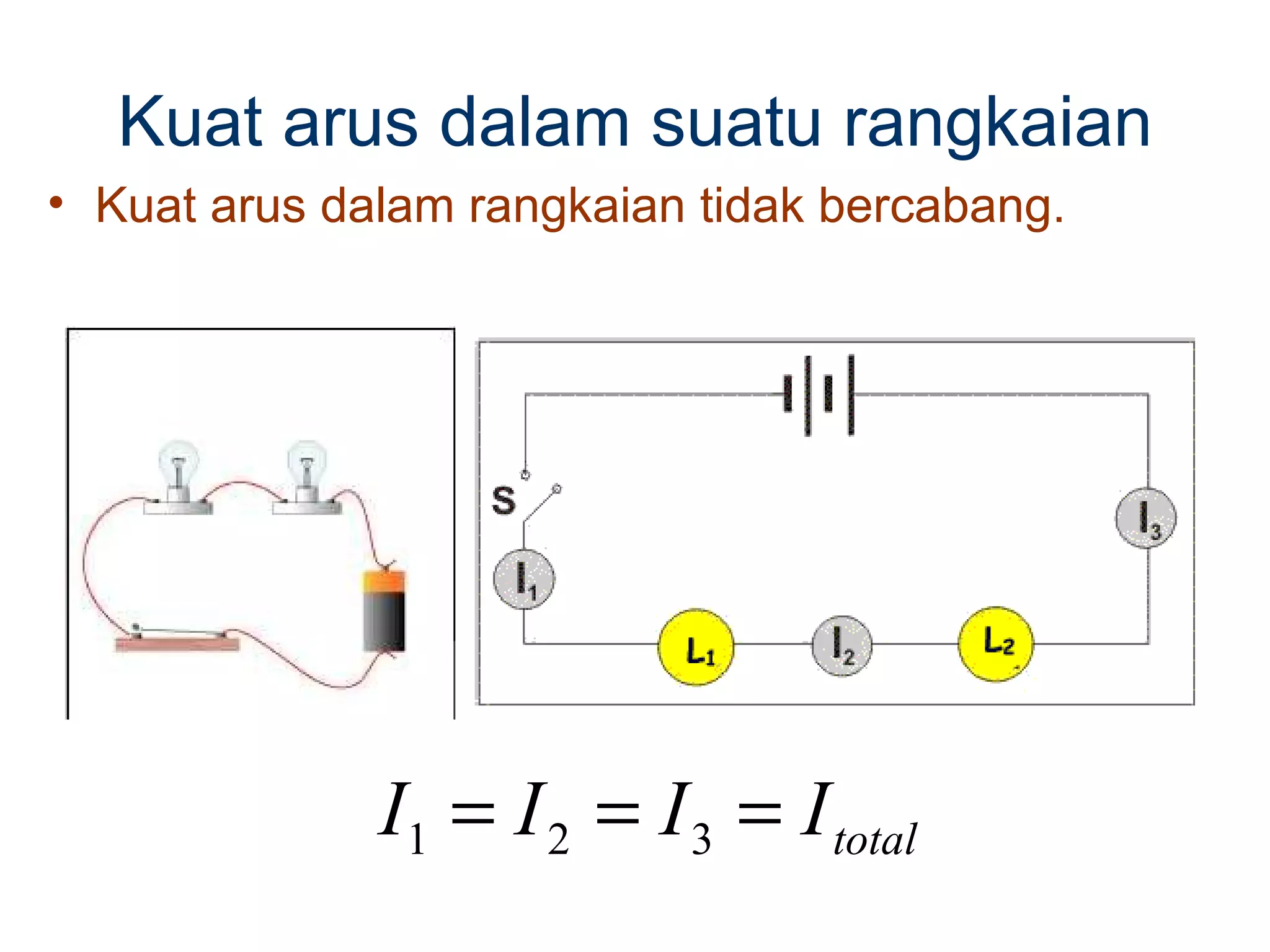
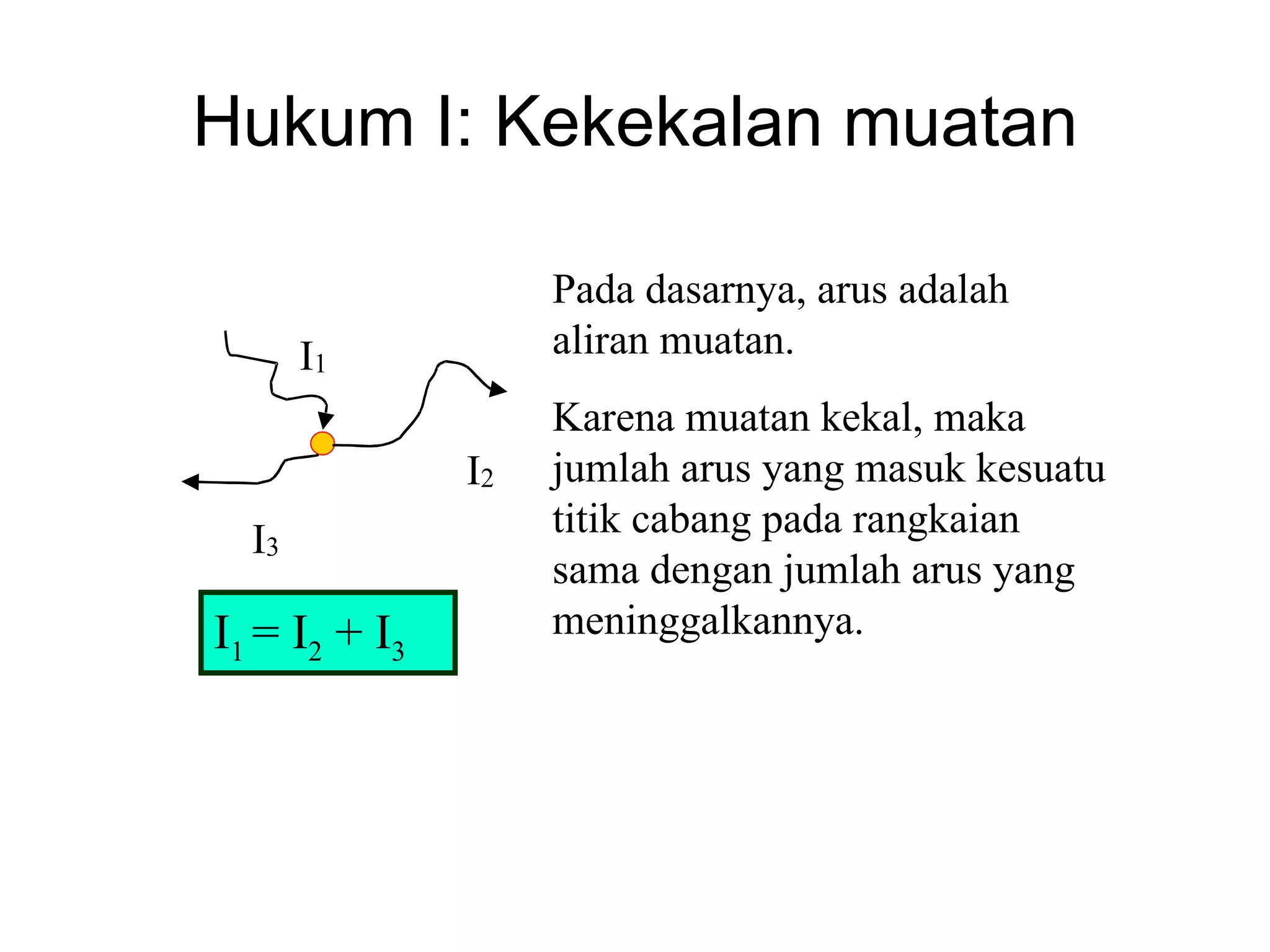
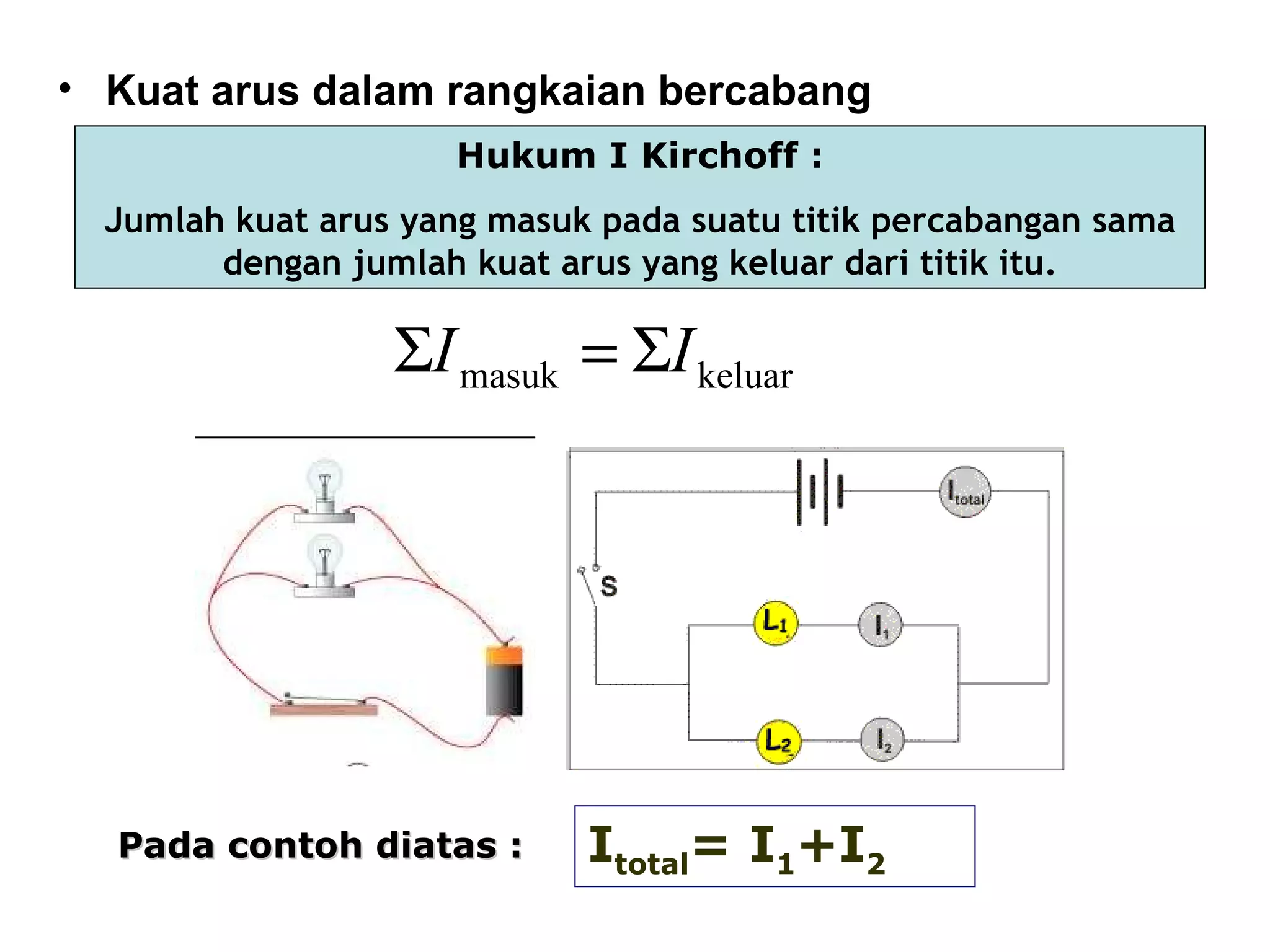
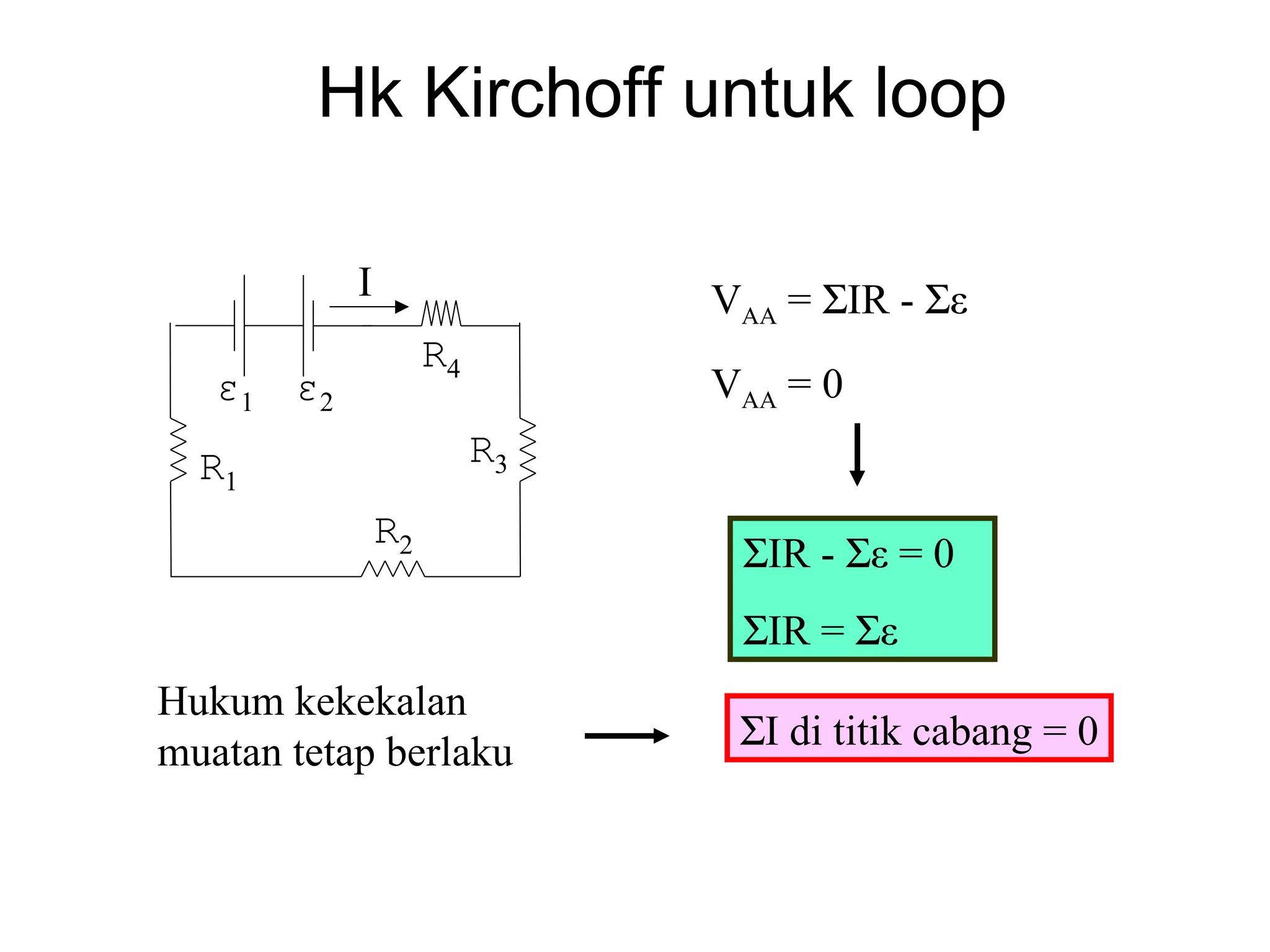
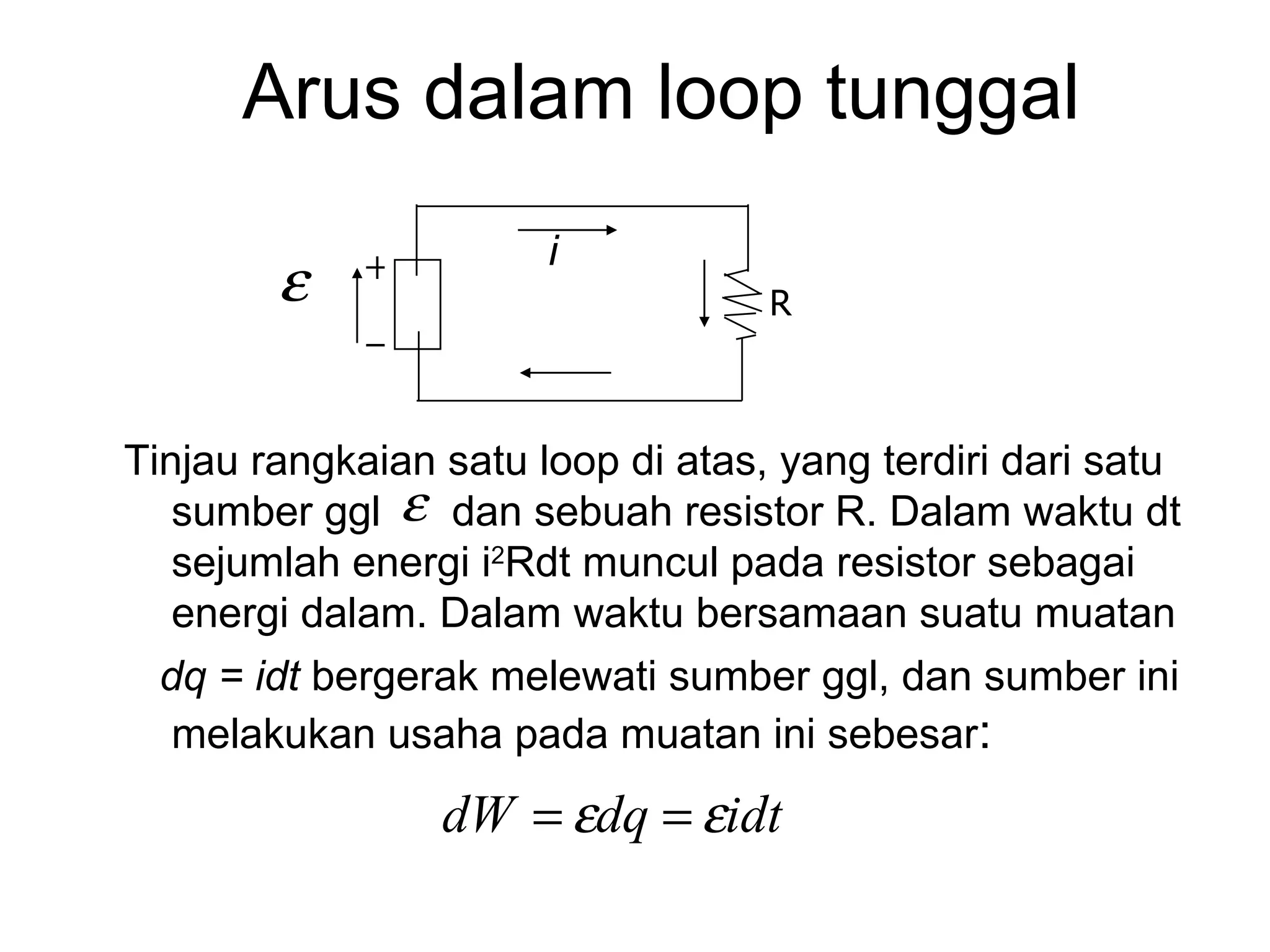
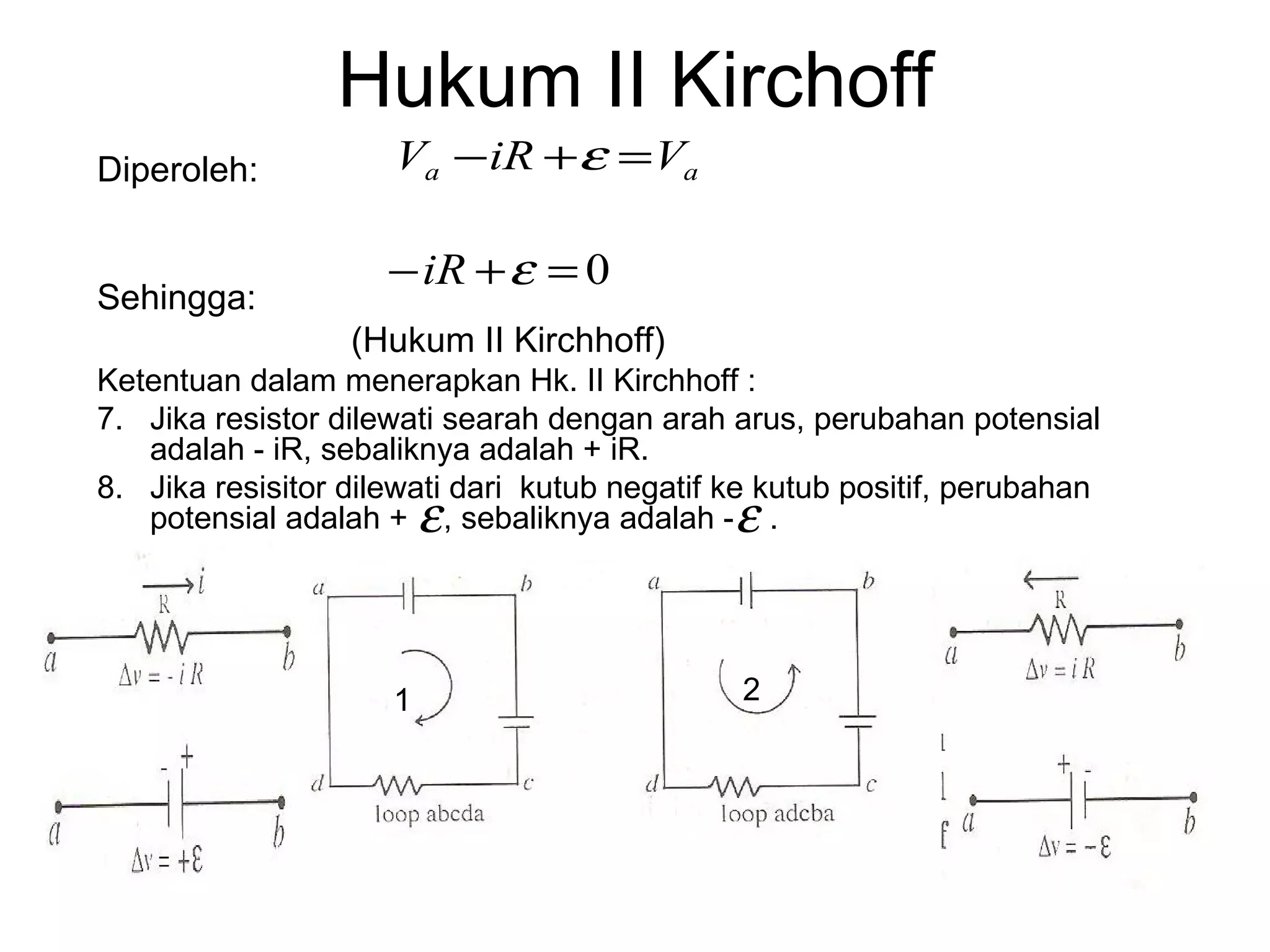
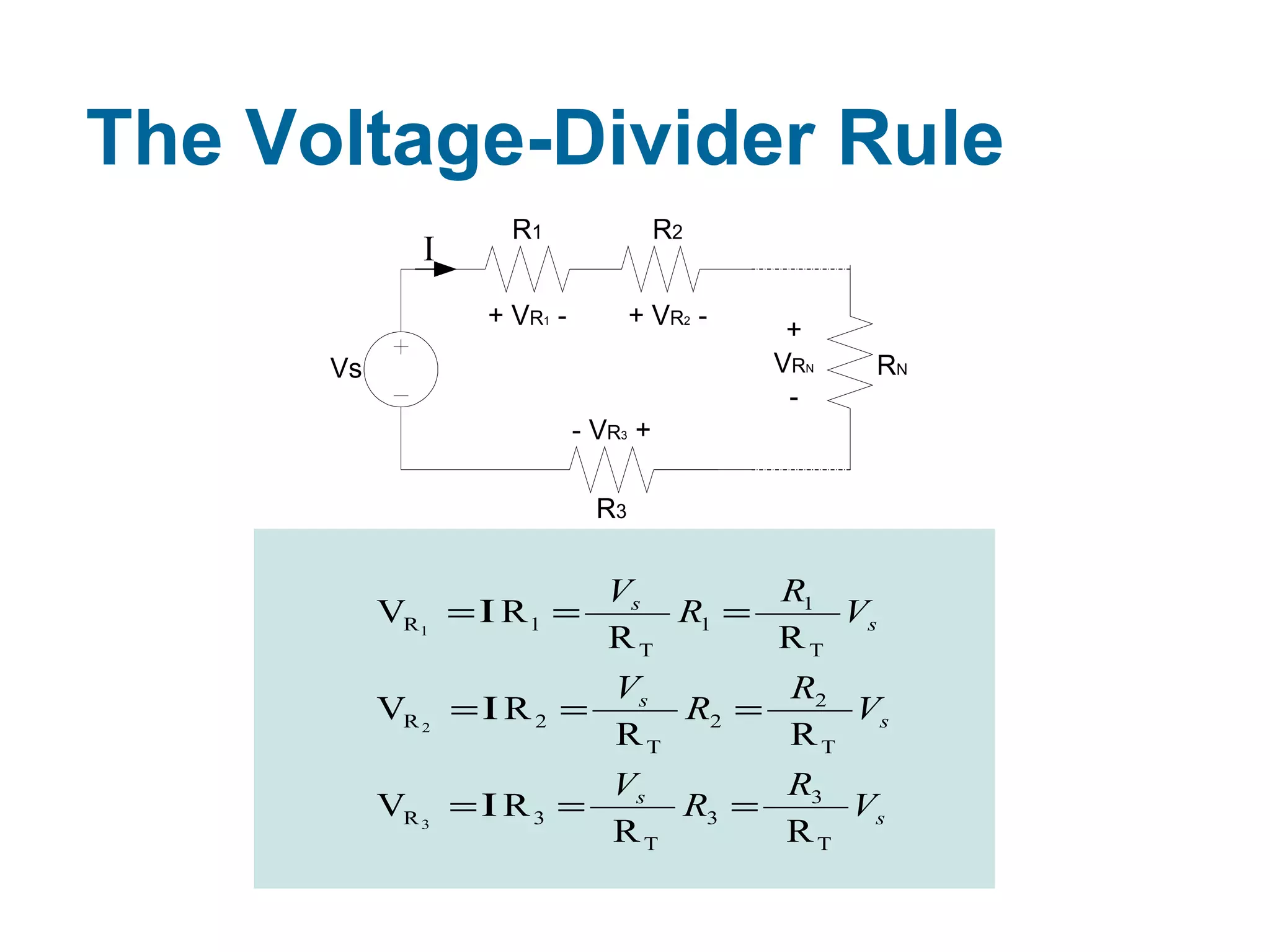
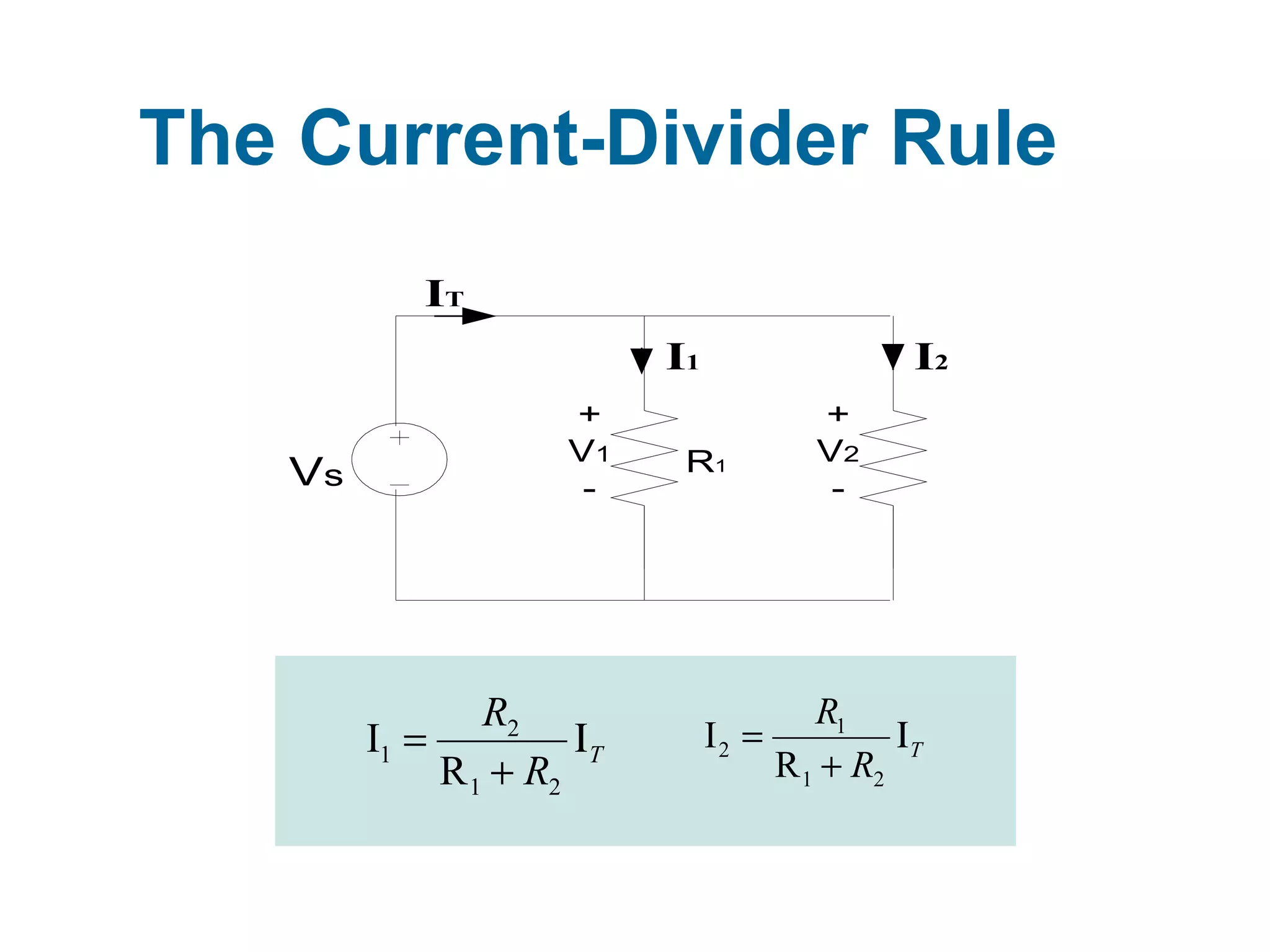
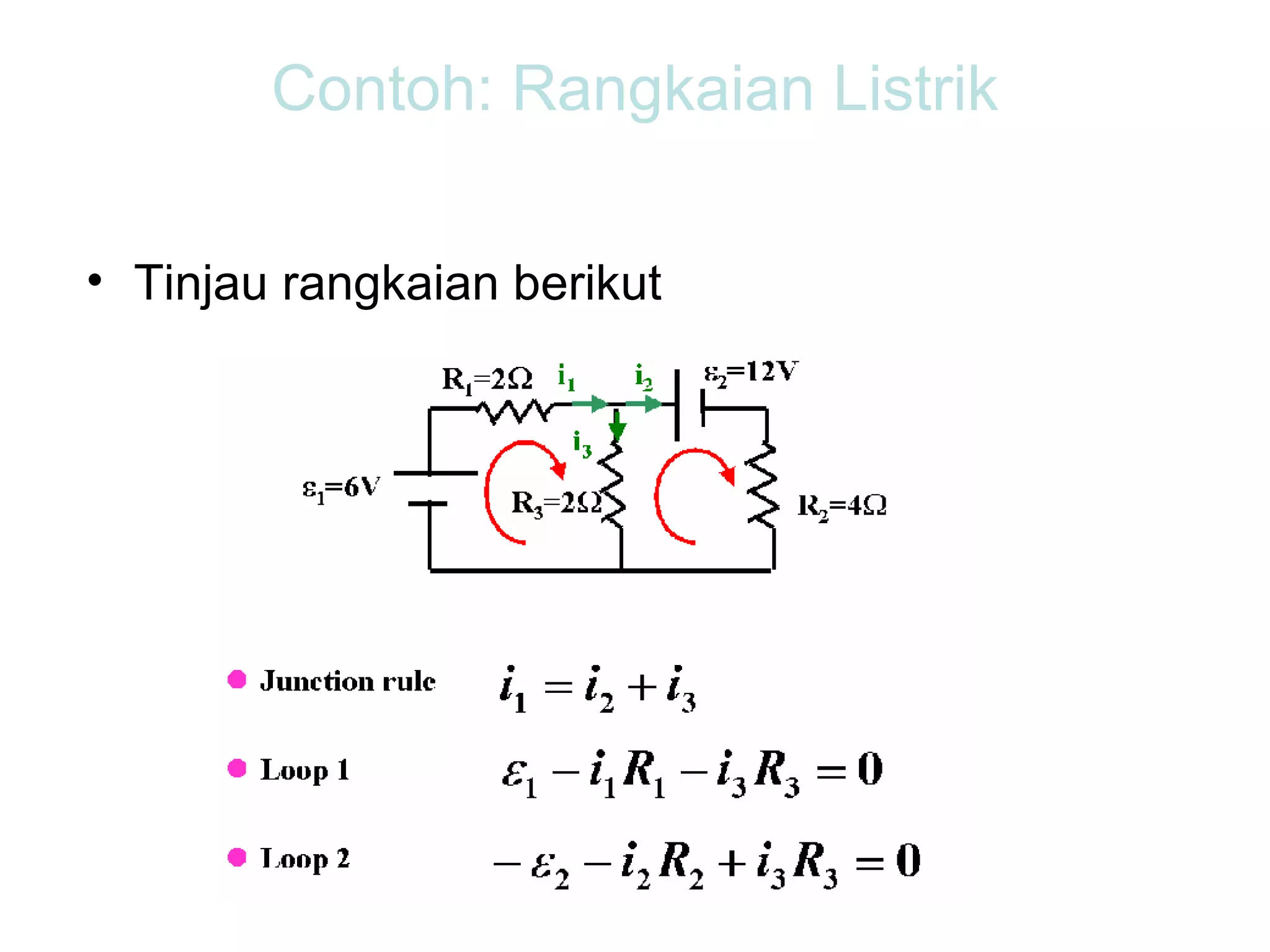
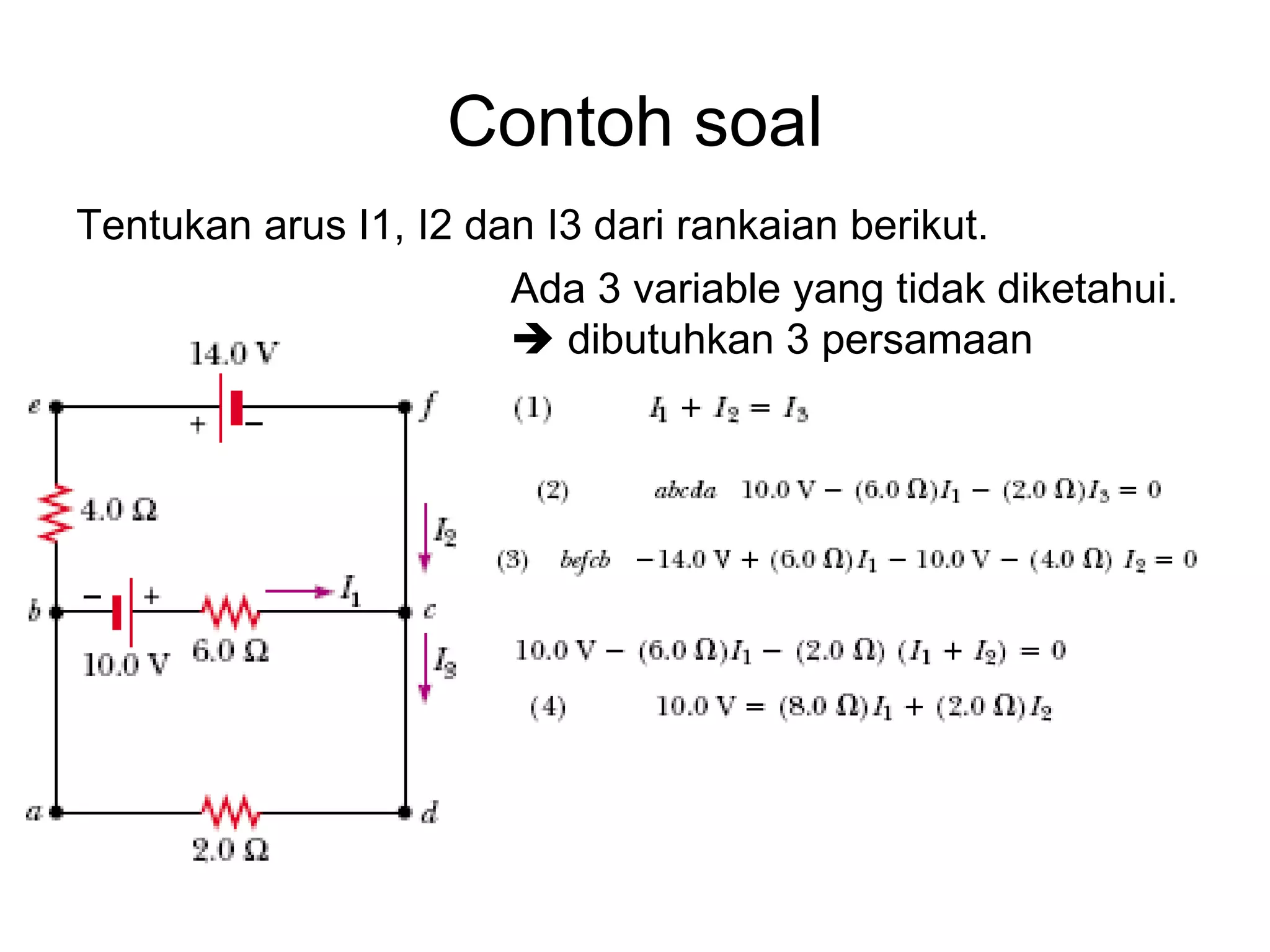
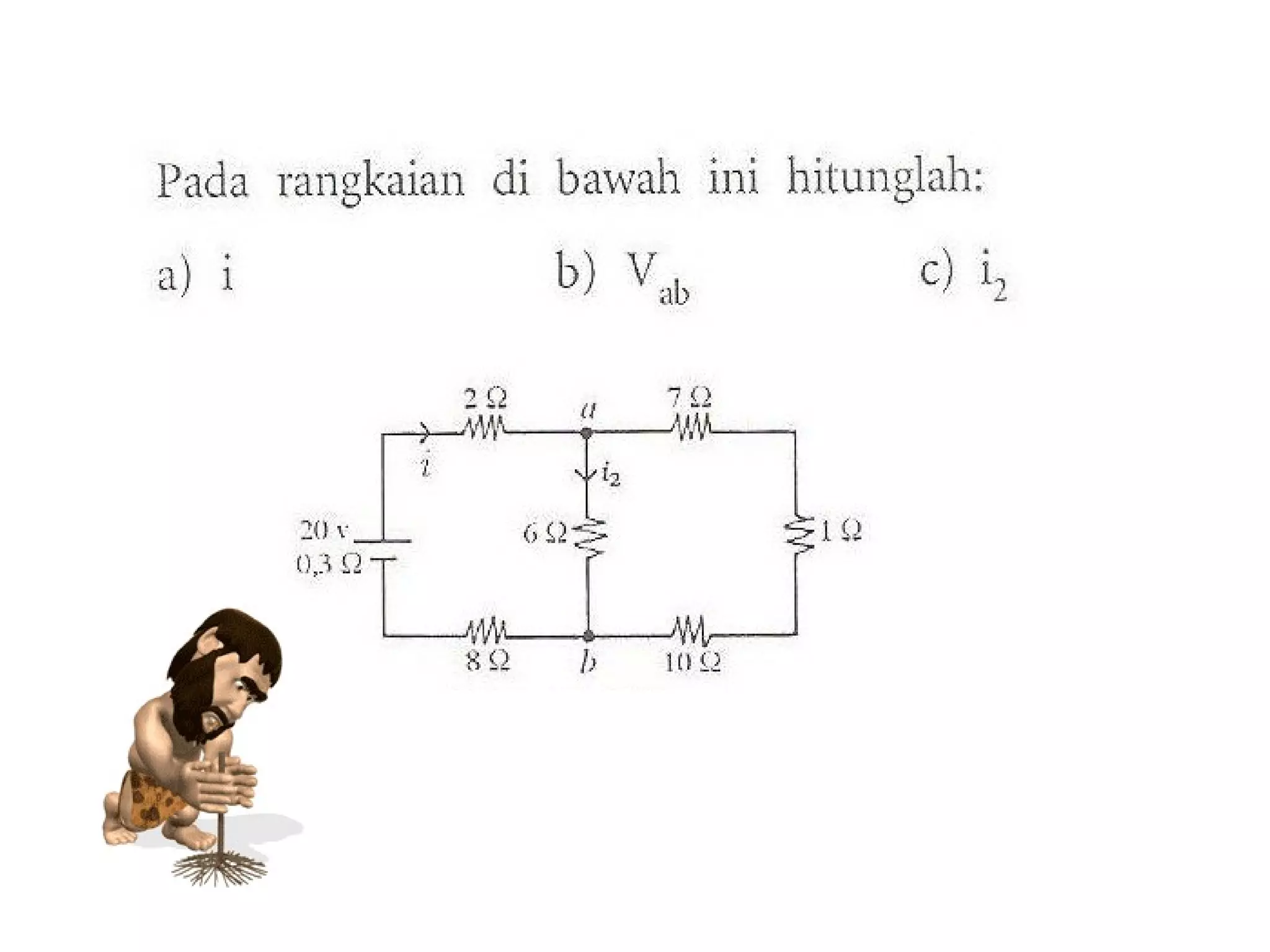
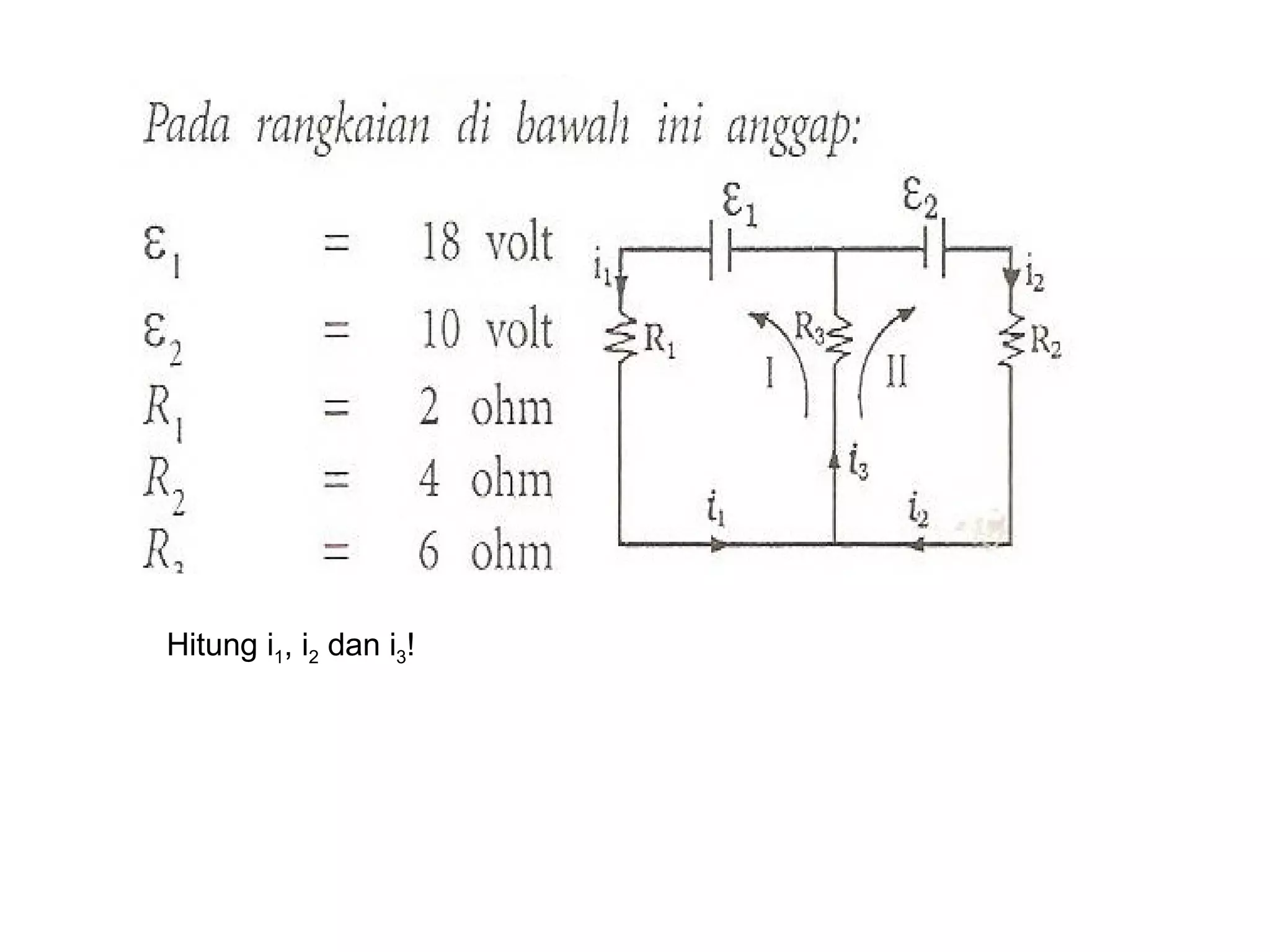
Dokumen tersebut membahas tentang hukum-hukum dasar listrik, yaitu Hukum Kirchhoff dan aturan-aturan terkait arus dan tegangan dalam rangkaian listrik tertutup. Di antaranya adalah hukum kekekalan muatan, hukum kekekalan energi, aturan pembagian tegangan dan pembagian arus. Contoh soal juga diberikan untuk mendemonstrasikan penerapan hukum-hukum tersebut dalam menentukan arus listrik d