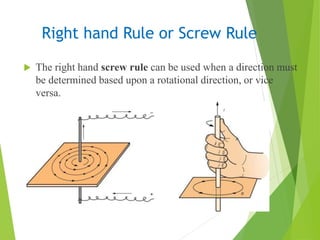
The document summarizes fundamental laws in electrical engineering, including Ohm's Law, Kirchhoff's Current and Voltage Laws, and Faraday's Laws of Electromagnetic Induction. It discusses the principles governing voltage, current, and resistance, as well as Lenz's Law and the concepts of voltage and current division. The document provides essential formulas and definitions related to these laws and their applications in electrical circuits.

1. BASIC LAWS USED IN ELECTRICAL
ENGINEERING

2. CONTENT
1. OHM’S LAW
2. KIRCHHOFF CURRENT LAW
3. KIRCHHOFF'S VOLTAGE LAW
4. VOLTAGE AND CURRENT DIVISION
RULE
5. LENZ LAW
6. SCREW LAW
7. FARADAY LAW OF ELECTROMAGNETIC
INDUCTION

3. Ohm’s Law
Georg Simon Ohm (1789 – 1854)
 German professor who publishes a book in 1827 that
includes what is now known as Ohm's law.
 Ohm's Law: The voltage across a resistor is directly
proportional to the current flowing through it.
 According to ohms law
V∞ I where R is constant
where, V = Voltage in Volts
I = Current in Amperes
R= Resistance in Ohms

4. Terminology Definition
 Voltage: A force that pushes the current through the circuit (in this
picture it would be equivalent to gravity).
 Current: The actual “substance” that is flowing through the wires of the
circuit (electrons!).
 Resistance: Friction that impedes flow of current through the circuit
(rocks in the river)

5. Gustav Robert Kirchhoff (1824 – 1887)
“Kirchhoff Law”
 Born in Prussia (now Russia), Kirchhoff developed his
"laws" while a student in 1845. These laws allowed him
to calculate the voltages and currents in multiple loop
circuits.

6. Kirchhoff Current Law KCL
 The algebraic sum of the currents entering a
node is zero or At any node the incoming
current is equal to outgoing current.
1i
5i
2i
3i
4i
1 2 3 4 5 0i i i i i    

7. Kirchhoff Voltage Law KVL
 In any closed path (or circuit) in a network, the algebraic sum of the IR
product is equal to the EMF in that path.
 In other words, in any closed loop (which also known as Mesh), the
algebraic sum of the EMF applied is equal to the algebraic sum of the
voltage drops in the elements. Kirchhoff’s second law is also known as
Voltage Law or Mesh law.
V0
I
R1
R2
V1
V2
A
+
+
-
-
0 1 2V V V 
Counter-clockwise:
0 1 2 0V V V   
2 1 0 0V V V   
Clockwise:

8. Voltage Division Rule
8
V0
I
R1
R2
V1
V2
A
0 0
1 2s
V V
I
R R R
 

 
0
2 2 2
1 2
V
V IR R
R R
 

 
2
2 0
1 2
R
V V
R R


 
1
1 0
1 2
Also
R
V V
R R



9. Current Division Rule
i(t) R1
i
R2
i1 i2 v(t)
+
-
1 2
1 2
( ) ( ) ( )p
R R
v t R i t i t
R R
 

2
1
1 1 2
( )
( ) ( )
Rv t
i t i t
R R R
 

1
2
2 1 2
( )
( ) ( )
Rv t
i t i t
R R R
 

Current divides in inverse proportion to the resistances

10. 10
Source Exchange
DC
sv
sR
abv
+
-
abv
+
-
sRs
s
v
R
ai 'ai
We can always replace a voltage source in series with a resistor by a current
source in parallel with the same resistor and vice-versa.
Doing this, however, makes it impossible to directly find the original source
current.

11. Lenz Law
 Lenz's law is named after the German scientist H. F. E. Lenz in
1834. Lenz's law obeys Newton's third law of motion (i.e to
every action there is always an equal and opposite reaction) and
the conservation of energy (i.e energy may neither be created nor
destroyed and therefore the sum of all the energies in the system
is a constant).

12. Statement:
 Lenz's law states that when an emf is generated by a change in magnetic
flux according to Faraday's Law, the polarity of the induced emf is such, that it
produces an current that's magnetic field opposes the change which produces it.
where,
ε = induced emf
δΦB = change in magnetic flux
N = No of turn of coil

13. Right hand Rule or Screw Rule
 The right hand screw rule can be used when a direction must
be determined based upon a rotational direction, or vice
versa.

14. Faraday 1st Laws of “Electromagnetic
induction”
 Whenever a conductor is placed in a varying
magnetic field an EMF gets induced across the
conductor (called as induced emf), and if the
conductor is a closed circuit then induced current
flows through it.
Magnetic field can be varied by various methods -
1. By moving magnet
2. By moving the coil
3. By rotating the coil relative to magnetic field.
 E = N (dΦ/dt) (volts)

15. Faraday 2nd Laws of
“Electromagnetic induction”
 The magnitude of induced emf is equal to the rate of
change of flux linkages with the coil. The flux linkages is
the product of number of turns and the flux associated
with the coil.

16. ANY QUERY…???
THANK YOU