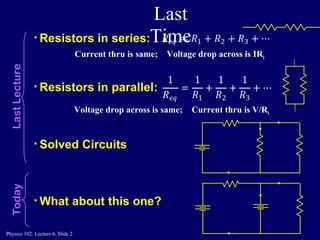
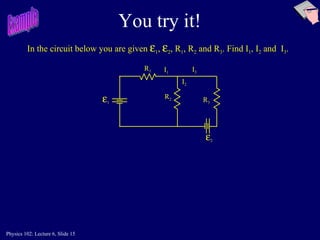
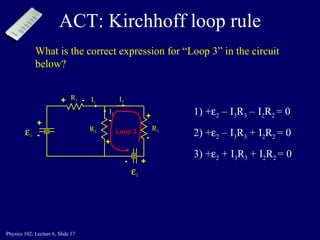
The document discusses Kirchhoff's laws, which describe how electric currents behave in circuits. It introduces Kirchhoff's Junction Rule, which states that the total current entering a junction equals the total current leaving it. It also introduces Kirchhoff's Loop Rule, which states that the sum of the voltage increases and decreases around any closed loop in a circuit is equal to zero. The document provides examples of how to apply these rules to solve for unknown currents in circuits. It also contains practice problems for students to work through applying Kirchhoff's laws.

1. Kirchhoff’s Laws Physics 102: Lecture 06

2. Last Time Resistors in series: Resistors in parallel: Current thru is same; Voltage drop across is IR i Voltage drop across is same; Current thru is V/R i Last Lecture Solved Circuits What about this one? Today

3. Kirchhoff’s Rules Kirchhoff’s Junction Rule (KJR): Current going in equals current coming out. Kirchhoff’s Loop Rule (KLR): Sum of voltage drops around a loop is zero.

4. Conceptual basis: conservation of charge At any junction in a circuit, the current that enters the junction equals the current that leaves the junction Example: Kirchhoff’s Junction Rule (KJR) At junction: I 1 + I 2 = I 3 R 1 R 2 R 3 I 1 I 3 I 2  1  2

5. Conceptual basis: conservation of energy Going around any complete loop in a circuit, the sum total of all the potential differences is zero Example: Kirchhoff’s Loop Rule (KLR) Around the right loop:  2 + I 3 R 3 + I 2 R 2 = 0 R 1 R 2 R 3 I 1 I 3 I 2  1  2

6. Using Kirchhoff’s Rules (1) Label all currents Choose any direction (2) Label +/- for all elements Current goes +  – (for resistors) Choose loop and direction Write down voltage drops Be careful about signs R 4 + - + + + + - - - - + + + - - - R 1 ε 1 R 2 R 3 ε 2 ε 3 R 5 A B I 1 I 3 I 2 I 4 I 5

7. Loop Rule Practice R 1 =5  I +  1 - IR 1 -  2 - IR 2 = 0 +50 - 5 I - 10 - 15 I = 0 I = +2 Amps  1 = 50V R 2 =15   2 = 10V A B Find I: Example Label currents Label elements +/- Choose loop Write KLR + - + - + - + -

8. ACT: KLR R 1 =10  E 1 = 10 V I B I 1 E 2 = 5 V R 2 =10  I 2 Resistors R 1 and R 2 are 1) in parallel 2) in series 3) neither + -

9. Preflight 6.1 R=10  E 1 = 10 V I B I 1 E 2 = 5 V R=10  I 2 1) I 1 = 0.5 A 2) I 1 = 1.0 A 3) I 1 = 1.5 A + - + - E 1 - I 1 R = 0 Calculate the current through resistor 1.  I 1 = E 1 /R = 1A

10. Preflight 6.1 R=10  E 1 = 10 V I B I 1 R=10  I 2 1) I 1 = 0.5 A 2) I 1 = 1.0 A 3) I 1 = 1.5 A + - + - E 1 - I 1 R = 0  I 1 = E 1 /R = 1A How would I 1 change if the switch was opened? E 2 = 5 V 1) Increase 2) No change 3) Decrease Calculate the current through resistor 1. ACT: Voltage Law

11. Preflight 6.2 R=10  E 1 = 10 V I B I 1 E 2 = 5 V R=10  I 2 1) I 2 = 0.5 A 2) I 2 = 1.0 A 3) I 2 = 1.5 A + - + - E 1 - E 2 - I 2 R = 0  I 2 = 0.5A Calculate the current through resistor 2.

12. Preflight 6.2 R=10  E 1 = 10 V I B I 1 E 2 = 5 V R=10  I 2 - + + - + E 1 - E 2 + I 2 R = 0 Note the sign change from last slide  I 2 = -0.5A Answer has same magnitude as before but opposite sign. That means current goes to the right, as we found before. How do I know the direction of I 2 ? It doesn’t matter. Choose whatever direction you like. Then solve the equations to find I 2. If the result is positive, then your initial guess was correct. If result is negative, then actual direction is opposite to your initial guess. Work through preflight with opposite sign for I 2 ?

13. Kirchhoff’s Junction Rule Current Entering = Current Leaving I 1 I 2 I 3 I 1 = I 2 + I 3 1) I B = 0.5 A 2) I B = 1.0 A 3) I B = 1.5 A I B = I 1 + I 2 = 1.5 A Calculate the current through battery. R=10  E 1 = 10 V I B I 1 E = 5 V R=10  I 2 + - Preflight 6.3

14. Kirchhoff’s Laws (1) Label all currents Choose any direction (2) Label +/- for all elements Current goes +  - (for resistors) Choose loop and direction Your choice! Write down voltage drops Follow any loops Write down junction equation I in = I out R 4 R 1 ε 1 R 2 R 3 ε 2 ε 3 I 1 I 3 I 2 I 4 R 5 A B

15. You try it! In the circuit below you are given  1 ,  2 , R 1 , R 2 and R 3 . Find I 1 , I 2 and I 3 . Example R 1 R 2 R 3 I 1 I 3 I 2  1  2

16. You try it! R 1 R 2 R 3 I 1 I 3 I 2 + - + + + Loop 1: +  1 - I 1 R 1 + I 2 R 2 = 0 Label all currents (Choose any direction) 2. Label +/- for all elements (Current goes +  - for resistor) 3. Choose loop and direction (Your choice!) Write down voltage drops (Potential increases or decreases?) - - - Loop 2:  1 5. Write down junction equation Node: I 1 + I 2 = I 3  2 3 Equations, 3 unknowns the rest is math! In the circuit below you are given  1 ,  2 , R 1 , R 2 and R 3 . Find I 1 , I 2 and I 3 . Loop 1  + -   +  1 - I 1 R 1 - I 3 R 3 -  2 = 0   Example Loop 2

17. ACT: Kirchhoff loop rule What is the correct expression for “Loop 3” in the circuit below? Loop 3 R 2 R 3  1  2 R 1 1) +  2 – I 3 R 3 – I 2 R 2 = 0 2) +  2 – I 3 R 3 + I 2 R 2 = 0 3) +  2 + I 3 R 3 + I 2 R 2 = 0 I 1 I 3 I 2 + - + + + - - - + -

18. Let’s put in real numbers In the circuit below you are given  1 ,  2 , R 1 , R 2 and R 3 . Find I 1 , I 2 and I 3 . Example 1. Loop 1: 20 -5I 1 +10I 2 = 0 2. Loop 2: 20 -5I 1 -10I 3 -2=0 3. Junction: I 3 =I 1 +I 2 solution: substitute Eq.3 for I 3 in Eq. 2: 20 - 5I 1 - 10(I 1 +I 2 ) - 2 = 0 rearrange: 15I 1 +10I 2 = 18 rearrange Eq. 1: 5I 1 -10I 2 = 20 Now we have 2 eq., 2 unknowns. Continue on next slide Loop 1 Loop 2  5 10 10 I 1 I 3 I 2 + - + + + - - -  + -

19. 15I 1 +10I 2 = 18 5I 1 - 10I 2 = 20 Now we have 2 eq., 2 unknowns. Add the equations together: 20I 1 =38 I 1 =1.90 A Plug into bottom equation: 5(1.90)-10I 2 = 20 I 2 =-1.05 A note that this means direction of I 2 is opposite to that shown on the previous slide Use junction equation (eq. 3 from previous page) I 3 =I 1 +I 2 = 1.90-1.05 I 3 = 0.85 A We are done!

20. See you next time…