Downloaded 33 times
Uploaded byAhmed Gamal
1 tension
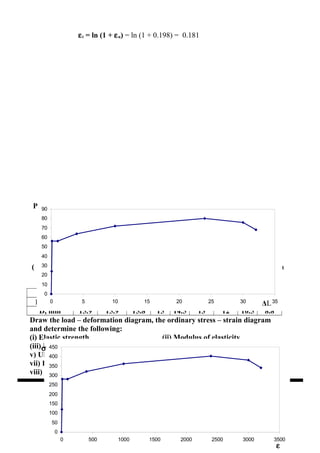
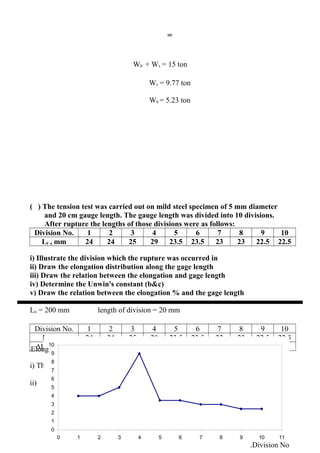
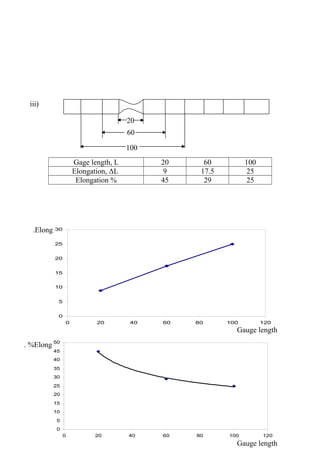
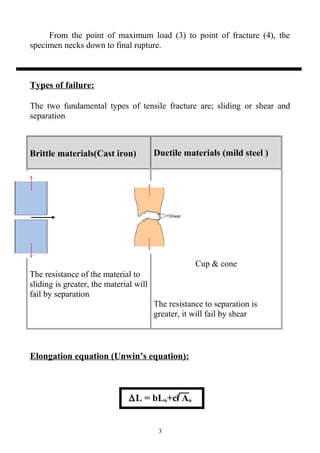
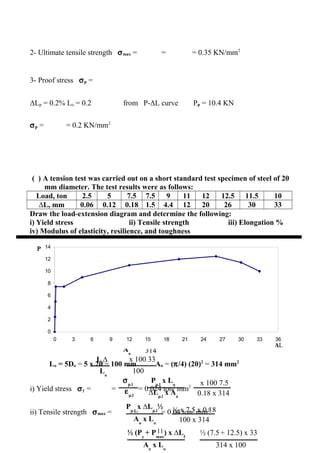
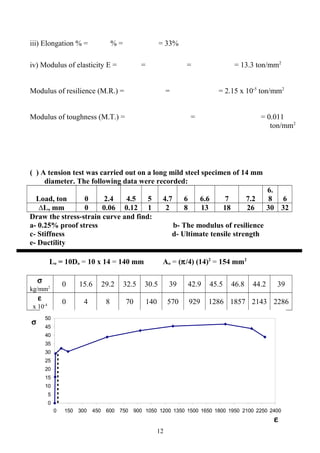
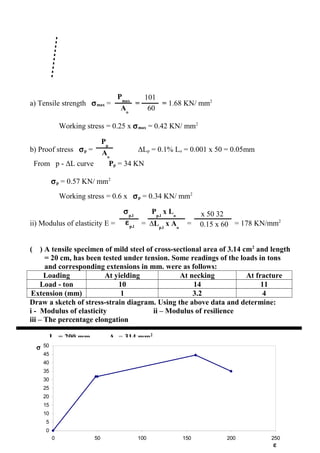
The document discusses concepts related to tension testing of materials including: - Stress-strain diagrams and key points like proportional limit, yield point, ultimate tensile strength - Ductile and brittle material behaviors - Calculations of properties from test data like modulus of elasticity, resilience, toughness - Effects of factors like carbon content, temperature, specimen geometry Worked examples are provided to calculate properties from given tension test load-extension data.
More Related Content
1 tension
- 1. P Aо ∆L Lo Tension Test ♦ ♦ Brittle materials 1-Cast iron 2- Concrete Brittleness: deformation Ductile materials Steel&Al Ductility: The ability of the material to be drawn under tensile load without fracture ORDINARY STRESS-STRAIN DIAGRAM 1 F F F F max max max y y p.l. p.l. p.l. ε ε ε ε σ σ σ
- 2. Stress σ =Strain ε = )σ- ε i) First Zone (Elasticity ) Elasticity Any changes in shape and dimensions is removed upon the removal of load a) From (0) loads to Proportional limit(P.L.) (1) b) From (1) to Elastic limit (E.L) ii) Second Zone a) From the (E.L) to the upper yield point (UYP), the material is partly elastic and partly plastic. b) From (UYP) to lower yield point (2), there is further increase in extension without any increase in load. c) From yield point (2) to maximum load point (3), the ductile stage. Plasticity Plasticity Permanent deformationyield iii) The Third Zone 2 3 4 21 UYP O σ ε
- 3. From the pointof maximum load (3) to point of fracture (4), the specimen necks down to final rupture. Types of failure: The two fundamental types of tensile fracture are; sliding or shear and separation Brittle materials(Cast iron) Ductile materials (mild steel ) The resistance of the material to sliding is greater, the material will fail by separation Cup & cone The resistance to separation is greater, it will fail by shear Elongation equation (Unwin’s equation): ∆L = bLо+c Aо 3
- 4. Elongation at gagelength (Plastic deformation) bLо Max Necking elongation c Aо 1- 2Lо % = b + neckingnecking Specimen For circular section Use Short Lо= 5.65 Aо Lо= 5Dо Brittle material Long Lо= 11.3 Aо Lо= 10Dо Ductile material Strength The external load required to overcome bonds between atoms 1- Stress at proportional limit 4 ∆L Lо Lо elong % ∆L Lo c Aо Lo
- 5. Pp.L Aо Pmax Aо Py Aо Pf Aо Pp Aо σy F.S σp F.S σp.l F.S The stress atthe last point of proportionality line between σ,ε σp.l = 2- Ultimate tensile strength σmax = 3- Yield stress σy = 4- Fracture stress σf = 5- Working stress σw = or or 6- Proof stress σp = working stress It is the stress which produced under a load of non-proportional elongation equal to certain specified percentage (0.1 – 0.5%) of the original gage length 5 ∆Lp ∆L p pp ∆Lp = (0.1 – 0.5)% x Lо
- 6. εp.l σp.l ∆Lp.l x Aо Pp.l x Lо Lо Aо ½Pp.l x∆Lp.l 7- Stiffness deformationE Modulus of elasticity (stiffness) E = = σ – ε 1- Initial tangent modulus E1 = tan θ1 2- Secant modulus E2 = tan θ2 3- Tangent modulus E3 = tan θ3 8- Resilience proportional lineP-∆L R = ½ Pp.l x ∆Lp.l Modulus of resilience (M.R) = 9- Toughness Brittle materialsDuctile materials 6 σ ε
- 7. Dо Di Lо Aо ½(Py +Pmax )∆Lf Lо Aо ⅔Pmax x ∆Lmax ∆Lf Lо Aо - Af Aо Pi Ai Modulusof toughness M.T. =M.T.= 10- Ductility % Elongation = %Reduction in area = 11- True stress and strain At Max. Point or before After Max. point or at any point True stress σt σt = σn(εn + 1) σt = True strain εt εt = ln (εn + 1) εt = 2ln True stress - strain curve n: Strain hardening exponent 7 % σt = k + m εt σt = k εt n σt = E εt σt εt
- 8. ∆Di /Do ∆Li /Lo k: Strength coefficient Provethat σt = σn (εn + 1) Assume constant volume AоLо = AiLi σn = σt = Ai = σt = σt = x = σn σt = σn(εn + 1) 12- Poisson ratio μ = •Factors affecting tension test (1) Carbon% Pp.l & Py σmax(ton/in2 ) = 27.06(1+K2 ) K = carbon% (2) Temperature 8 Lо Aо A1 A2 L1 L2 P1 P2 Pi Aо Pi Ai Aо Lо Li Pi Li Aо Lо Pi Aо Li Lо ∆L + Lо Lо 0.15%C ε σ 0.6%C 0.8%C
- 9. 250°Cductilitytensile strengthE (3) Testspeed ductility (4) Cross-section shape (5) Overstrain Pp.lyield stress •Yield phenomena yieldyield Yield point P 0 2 4 6 5. 5 7 P 0 2 4 6 6 8 ∆L 0 0.02 0.0 4 0.06 1 3 ∆L 0 0.02 0.04 0.06 1 5 •Necking 1neck 245°45° Hyper-elastic resilience resilience 9
- 10. εp.l σp.l ∆Lp.l x Aо Pp.l x Lо 0.1x 50.3 10x 100 Pmax Aо 17.5 50.3 Pp Aо 10.4 50.4 Resilience Hyper-elastic resilience Hysteresis SHEET 1 ( ) A tension test was carried out on a steel specimen of 8 mm diameter. The following data were obtained for the load P in KN and extension ΔL on a gage length of 100 mm: P (KN) 0 5 8 10 13 15 16.5 17.5 17 15 ∆L (mm) 0 0.05 0.08 0.1 1.5 3.5 6 9 11 15 Draw the load-extension diagram and determines: (i) Modulus of elasticity (ii) 0.2% proof stress (iii) Ultimate tensile strength (iv) Draw the fracture shape of the tested specimen Aо = (π/4) (8)2 = 50.3 mm2 1- Modulus of elasticity E = = = = 198.8 KN/mm2 10 0 2 4 6 8 10 12 14 16 18 20 0 2 4 6 8 10 12 14 16 P ΔL Proof point
- 11. Pmax Aо 12.5 314 Py Aо 7.5 314 ∆Lf Lо 33x 100 100 εp.l σp.l ∆Lp.l x Aо Pp.l xLо 0.18 x 314 7.5x 100 Aо x Lо ½Pp.l x ∆Lp.l 100 x 314 ½ x 7.5 x 0.18 Aо x Lо ½ (Py + Pmax ) x ∆Lf 314 x 100 ½ (7.5+ 12.5) x 33 2- Ultimate tensile strength σmax = = = 0.35 KN/mm2 3- Proof stress σp = ΔLp = 0.2% Lo = 0.2 from P-ΔL curve Pp = 10.4 KN σp = = 0.2 KN/mm2 ( ) A tension test was carried out on a short standard test specimen of steel of 20 mm diameter. The test results were as follows: Load, ton 2.5 5 7.5 7.5 9 11 12 12.5 11.5 10 ∆L, mm 0.06 0.12 0.18 1.5 4.4 12 20 26 30 33 Draw the load-extension diagram and determine the following: i) Yield stress ii) Tensile strength iii) Elongation % iv) Modulus of elasticity, resilience, and toughness Lо = 5Dо = 5 x 20 = 100 mm Aо = (π/4) (20)2 = 314 mm2 i) Yield stress σy = = = 0.024 ton/ mm2 ii) Tensile strength σmax = = = 0.04 ton/ mm2 11 0 2 4 6 8 10 12 14 0 3 6 9 12 15 18 21 24 27 30 33 36 P ΔL
- 12. iii) Elongation %= % = = 33% iv) Modulus of elasticity E = = = = 13.3 ton/mm2 Modulus of resilience (M.R.) = = = 2.15 x 10-5 ton/mm2 Modulus of toughness (M.T.) = = = 0.011 ton/mm2 ( ) A tension test was carried out on a long mild steel specimen of 14 mm diameter. The following data were recorded: Load, ton 0 2.4 4.5 5 4.7 6 6.6 7 7.2 6. 8 6 ∆L, mm 0 0.06 0.12 1 2 8 13 18 26 30 32 Draw the stress-strain curve and find: a- 0.25% proof stress b- The modulus of resilience c- Stiffness d- Ultimate tensile strength e- Ductility Lо = 10Dо = 10 x 14 = 140 mm Aо = (π/4) (14)2 = 154 mm2 σ kg/mm2 0 15.6 29.2 32.5 30.5 39 42.9 45.5 46.8 44.2 39 ε x 10-4 0 4 8 70 140 570 929 1286 1857 2143 2286 12 0 5 10 15 20 25 30 35 40 45 50 0 150 300 450 600 750 900 1050 1200 1350 1500 1650 1800 1950 2100 2250 2400 σ ε
- 13. Pp Aо Aо x Lо ½Pp.l x ∆Lp.l 140x 154 ½ x 4.5 x 0.12 Pmax Aо 7.2 154 ∆Lf Lо 32x 100 140 εp.l σp.l ∆Lp.l x Aо Pp.l x Lо 0.12 x 154 4.5x 140 Aо x Lо ½Pp.l x ∆Lp.l 140 x 154 ½ x 4.5 x 0.12 Pmax Aо 7.2 154 ∆Lf Lо 32x 100 140 εp.l σp.l ∆Lp.l x Aо Pp.l x Lо 0.12 x 154 4.5x 140 Py Aо 4.3 154 Pmax Aо 7.2 154 ΔL Lо 26 140 a- Proof stress σp = ΔLp = 0.25% Lo = 0.35mm ε = 0.35/140 = 25 x 10-4 From σ - ε curve σp = 30 kg/ mm2 b- Modulus of resilience (M.R.) = = = 1.25 x 10-5 ton/mm2 c- Modulus of elasticity E = = = = 34.1 ton/mm2 d- Tensile strength σmax = = = 0.047 ton/ mm2 e- Elongation % = % = = 23% ( ) A tension test was carried out on a long mild steel specimen of 14 mm diameter. The following data were recorded: Load, ton 0 2.4 4.5 4.3 5.1 6 6.6 7 7.2 6. 8 6 ∆L, mm 0 0.06 0.12 0.1 5 3 8 13 18 26 30 32 Calculate: a- The yield stress b- The modulus of resilience c- Stiffness d- Ultimate tensile strength e- Ductility f- True stress and true strain at initial necking Lо = 10Dо = 10 x 14 = 140 mm Aо = (π/4) (14)2 = 154 mm2 a- Yield stress σy = = = 0.028 ton/ mm2 b- Modulus of resilience (M.R.) = = = 1.25 x 10-5 ton/mm2 c- Modulus of elasticity E = = = = 34.1 ton/mm2 d- Tensile strength σmax = = = 0.047 ton/ mm2 e- Elongation % = % = = 23% 13
- 14. f- Initial neckingat max. Point σn = = = 0.047 ton/ mm2 εn = = = 0.186 σt = σn (1 + εn) = 0.047(1 + 0.186) = 0.056 ton/ mm2 εt = ln (1 + εn) = ln (1 + 0.186) = 0.171 ( ) A tension test was carried out on a metallic road of 50 mm2 cross-sectional area, and 100 mm gage length. The load in KN and the corresponding extension in mm are as follows: P (KN) 0 5 8 10 13 15 16.5 17.5 17 15 ∆L (mm) 0 0.05 0.08 0.1 1.5 3.5 6 9 11 15 Draw nominal stress-strain diagrams and determine the following: (i) 0.2% proof stress (ii) Modulus of elasticity (iii) Tensile strength (iv) Elongation percent v) Modulus of toughness Lо = 100 mm Aо = 50 mm2 σ (N/mm2 0 100 160 200 260 300 330 350 340 300 ε (x 10-4 ) 0 5 8 10 150 350 600 900 110 0 1500 14 0 50 100 150 200 250 300 350 400 0 150 300 450 600 750 900 1050 1200 1350 1500 σ ε
- 15. Pp Aо Pmax Aо 17.5 50 ∆Lf Lо 15x 100 100 εp.l σp.l ∆Lp.l x Aо Pp.l xLо 0.1 x 50 10x 100 Aо x Lо ½ (Py + Pmax ) x ∆Lf 50 x 100 ½ (10.5+ 17.5) x 15 Pmax Aо 1.75 50 εp.l σp.l ∆Lp.l x Aо Pp.l x Lо 0.1 x 50 1x 100 Aо x Lо ½ (Py + Pmax ) x ∆Lf 50 x 100 ½ (1+ 1.75) x 15 ∆Lf Lо 15x 100 100 i) Proof stress σp = ΔLp = 0.2% Lo = 0.2mm ε = 0.2/100 = 20 x 10-4 From σ - ε curve σp = 210 N/ mm2 Pp = 10.5KN ii) Modulus of elasticity E = = = = 200 KN/mm2 iii) Tensile strength σmax = = = 0.35 KN/ mm2 iv) Elongation % = % = = 15% Modulus of toughness (M.T.) = = = 0.042 KN/mm2 ( ) A tension test was carried out on a steel test specimen with cross-section area equals to 50 mm2 , and 100 mm gage length. The test results were as follows: Load (ton) 0.5 0.8 1 1.3 1.5 1.65 1.75 1.7 1.5 Extension (mm) 0.05 0.08 0.1 1.5 3.5 6 9 11 15 Draw the load – extension diagram and determine: (i) Tensile strength (ii) Modulus of elasticity (iii) Modulus of toughness (iv) Elongation % Draw the fracture shape of the tested specimen Lо = 100 mm Aо = 50 mm2 15 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 P ΔL
- 16. i) Tensile strengthσmax = = = 0.035 ton/mm2 ii) Modulus of elasticity E = = = = 20 ton/mm2 iii) Modulus of toughness = = = 0.0042 KN/mm2 iv) Elongation % = % = = 15% ( ) A tension test was carried out on a long specimen of 8 mm diameter and the following data were recorded: P (KN) 0 5 8 11 13 15 16.5 17.5 17 15 ∆L (mm) 0 0.05 0.08 0.1 1.5 3.5 6 9 11 15 Draw the stress-strain diagram and calculate the following: i- Stiffness ii- 0.2% proof stress iii- Ductility iv- True stress and strain at initial necking v- Describe the fracture characteristic of the test specimen vi- Design a structural element of round cross section area from the same material to carry a load of 3 ton if the factor of safety is 1.5 Lо = 10 Dо = 80 mm Aо = π/4 (8)2 = 50.3 mm2 σ (N/mm2 0 99.6 159.4 219 259 299 328.7 348. 6 338. 6 298.8 ε (x 10-4 ) 0 6.25 10 12.5 187. 5 437.5 750 1125 1375 1875 160 50 100 150 200 250 300 350 400 0 200 400 600 800 1000 1200 1400 1600 1800 2000 σ ε
- 17. εp.l σp.l ∆Lp.l x Aо Pp.l x Lо 0.1x 50.3 11x 80 Pp Aо ∆Lf Lо 15x 100 80 Pmax Aо 17.5 50.3 ΔL Lо 9 80 σp F.S. 238 1.5 30000 π/4 D2 i) Modulus of elasticity E = = = = 175 KN/mm2 ii) Proof stress σp = ΔLp = 0.2% Lo = 0.16mm ε = 0.16/80 = 20 x 10-4 From σ - ε curve σp = 238 N/ mm2 Pp = 12 KN iii) Elongation % = % = = 19% iv) Initial necking at max. Point σn = = = 0.348 KN/ mm2 εn = = = 0.1125 σt = σn (1 + εn) = 0.348(1 + 0.1125) = 0.387 ton/ mm2 εt = ln (1 + εn) = ln (1 + 0.1125) = 0.107 v) Fracture shape is cup and cone due to shear stresses vi) σp = 238 N/ mm2 , P = 3 ton = 30 KN Working stress = = = 158.7 N/ mm2 158.7 = D = 15.5 mm 17
- 18. ( ) Thefollowing results were obtained in a tensile test of a test piece with a 50 mm gauge length and a cross-sectional area of 60 mm2 : P (KN) 12 25 32 36 40 42 63 80 93 100 101 90 ∆L (mm) 0.0 5 0. 1 0.1 5 0.2 0.2 5 0.3 1.2 5 2.5 3.75 5 6.2 5 7.5 The elongation and reduction of area were 16% and 64% respectively. i- Calculate the maximum allowable working stress if this is to equal (a) 0.25 x tensile strength (b) 0.6 x 0.1% proof stress ii- Calculate the Young's modulus iii- What would have been the elongation and reduction of area if a 150 mm gauge length had been used? Lо = 50 mm Aо = 60 mm2 180 10 20 30 40 50 60 70 80 90 100 110 0 1 2 3 4 5 6 7 8 P ΔL
- 19. Pp Aо Pmax Aо 101 60 εp.l σp.l ∆Lp.l x Aо Pp.l x Lо 0.15x 60 32x 50 a) Tensile strength σmax = = = 1.68 KN/ mm2 Working stress = 0.25 x σmax = 0.42 KN/ mm2 b) Proof stress σp = ΔLp = 0.1% Lo = 0.001 x 50 = 0.05mm From p - ΔL curve Pp = 34 KN σp = 0.57 KN/ mm2 Working stress = 0.6 x σp = 0.34 KN/ mm2 ii) Modulus of elasticity E = = = = 178 KN/mm2 ( ) A tensile specimen of mild steel of cross-sectional area of 3.14 cm2 and length = 20 cm, has been tested under tension. Some readings of the loads in tons and corresponding extensions in mm. were as follows: Loading At yielding At necking At fracture Load - ton 10 14 11 Extension (mm) 1 3.2 4 Draw a sketch of stress-strain diagram. Using the above data and determine: i - Modulus of elasticity ii – Modulus of resilience iii – The percentage elongation Lо = 200 mm Aо = 314 mm2 σ (kg/ mm2 ) 0 31.85 44.59 35 ε x 10-4 0 50 160 200 190 5 10 15 20 25 30 35 40 45 50 0 50 100 150 200 250 σ ε
- 20. εp.l σp.l ∆Lp.l x Aо Pp.l x Lо 1x 314 10x 200 ∆Lf Lо 4x 100 200 Aо x Lо ½Pp.l x ∆Lp.l 314 x 200 ½ x 10 x 1 Pmax Aо 140 412 ΔL Lо 53.5 200 Dо Di 2 ln 22.9 18 2 ln ii) Modulus of elasticity E = = = = 6.4 ton/mm2 b- Modulus of resilience (M.R.) = = = 8 x 10-5 ton/mm2 iii) Elongation % = % = = 2% ( ) A tension test was carried out on a low carbon steel test specimen having a gage length of 200 mm. The measured loads in KN and extensions in mm were as follows: Load (KN) 0 86 122 134 140 138 116 Extension (mm) 0 6 15 25.8 39.6 53.5 70.5 Diameter mm 22.9 22.6 22 21.6 20.9 18 14.8 Determine: i- The ultimate tensile strength ii- The ordinary strain and true strain at a load = 138 KN Lо = 200 mm Aо = π/4 (22.9)2 = 412 mm2 Ultimate tensile strength σmax = = = 0.34 KN/ mm2 The ordinary strain εn = = = 0.27 20
- 21. The true strainεt = = = 0.48 ( ) A tension test was carried out on a low carbon steel test specimen of 200 mm gage length and the following data was recorded: P (KN) 0 86 122 134 140 138 116 ΔL, mm 0 6 15 25.8 39.6 53.5 70.5 D, mm 22.9 22.6 22 21.6 20.9 18 14.8 Draw the true stress – true strain diagram and determine the following: i) The tensile strength and the true stress at initial necking ii) The strain hardening exponent and strength coefficient iii) The ordinary and true strain at fracture iv)The strain hardening coefficient v)The ordinary and true strain at initial necking Lо = 200 mm Aо = π/4 (22.9)2 = 412 mm2 σt = (Pi/Ai) 0 214.4 321 366 408.3 542.6 674.6 εt = (2 ln Do/Di) 0 0.026 0.08 0.117 0.183 0.482 0.873 210 100 200 300 400 500 600 700 800 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 σt εt
- 22. Pmax Aо 140 412 Pmax Ai 140 343 ΔL Lо 70.5 200 Dо Di 2 ln 22.9 14.8 2 ln ΔL Lо 39.6 200 Dо Di 2ln 22.9 20.9 2 ln i) Initial necking at max. Point Ai = π/4 (20.9)2 = 343 mm2 σn = = = 0.34 KN/ mm2 σt = = = 0.41 KN/ mm2 ii) Between max. Point and proportional limit, σt = k εt n ln σt = ln k + n ln εt ln 321 = ln k + n ln 0.08 (1) ln 366 = ln k + n ln 0.117 (2) From 1 , 2 n = 0.344 k = 6.64 iii) At fracture The ordinary strain εn = = = 0.35 The true strain εt = = = 0.87 iii) At initial necking The ordinary strain εn = = = 0.198 The true strain εt = = = 0.183 22
- 23. εt = ln(1 + εn) = ln (1 + 0.198) = 0.181 ( ) A tension test was carried out on a steel bar 15.9 mm diameter and 100 mm gage length, The loads in KN, the corresponding extension in mm, and minimum diameter in mm during the test were as follows: P (KN) 0 24 56 56 64 72 80 76 68 Ext., mm 0 0.06 0.14 1 4 10 24 30 32 D, mm 15.9 15.9 15.8 15 14.5 13 12 10.5 8.8 Draw the load – deformation diagram, the ordinary stress – strain diagram and determine the following: (i) Elastic strength (ii) Modulus of elasticity (iii) Modulus of resilience (iv) Elongation percent v) Ultimate tensile strength vi) Modulus of toughness vii) Percentage reduction of area viii) The strength coefficient and strain hardening exponent Lо = 100 mm Aо = π/4 (15.9)2 = 199 mm2 23 0 10 20 30 40 50 60 70 80 90 0 5 10 15 20 25 30 35 P ΔL 0 50 100 150 200 250 300 350 400 450 0 500 1000 1500 2000 2500 3000 3500 σ ε
- 24. εp.l σp.l ∆Lp.l x Aо Pp.l x Lо 0.14x 199 56x 100 Pmax Aо 80 199 56 199 Pp.l Aо ∆Lf Lо 32x 100 100 Aо x Lо ½Pp.l x ∆Lp.l 199 x 100 ½ x 56 x 0.14 Aо x Lо ½ (Py + Pmax ) x ∆Lf 199 x 100 ½ (56+ 80) x 32 Aо Ao - Af 199 199 – 60.8 σ 0 120. 6 281.4 281.4 321.6 361.8 402 381.9 341.7 ε x 10-4 0 6 14 100 400 1000 2400 3000 3200 i) Elastic strength σp.l = = = 0.281 KN/mm2 ii) Modulus of elasticity E = = = = 201 KN/mm2 iii) Modulus of resilience (M.R.) = = = 2 x 10-4 KN/mm2 iv) Elongation % = % = = 32% v) Ultimate tensile strength σmax = = = 0.4 KN/mm2 24
- 25. vi) Modulus oftoughness = = = 0.11KN/mm2 vii) Percent reduction of area = = = 69.4% Af = π/4 (8.8)2 = 60.8 mm2 ( ) A tension test was carried out on a long standard test specimen of mild steel of 16 mm diameter. The test results were recorded as follows: • At load 2.4 ton the extension was 0.06 mm • The load at proportional limit was 4.8 ton • At load 5.2 ton the extension was 3 mm • The max. load was 7.2 ton and the corresponding extension was 26 mm • The length of specimen just before fracture was 192 mm at load equals 6 ton (i) Draw a sketch of load – extension diagram for this test specimen (ii) Determine the tensile strength and elongation % (iii) Calculate the modulus of resilience and modulus of toughness (iv) What is the failure shape of this test specimen P.l. Max. Failure P (ton) 2.4 4.8 5.2 7.2 6 ∆L (mm( 0.06 X 3 26 Y Lо = 10 Dо = 10 x 16 = 160 mm Aо = π/4 (16)2 = 201 mm2 25
- 26. 0 1 2 3 4 5 6 7 8 0 2 46 8 10 12 14 16 18 20 22 24 26 28 30 32 34 P ∆Lf 4.8 X 2.4 0.06 Pmax Aо 7.2 201 ∆Lf Lо 32x 100 160 Aо x Lо ½Pp.l x ∆Lp.l 201 x 160 ½ x 4.8 x0.12 Aо x Lо ½ (Py + Pmax ) x ∆Lf 201 x 160 ½ (4.8+ 7.2) x 32 Y = Lf - Lо = 192 – 160 = 32 mm = ∆Lf = X = 0.12 mm ii) Tensile strength σmax = = = 0.036 ton/mm2 Elongation % = % = = 20% iii) Modulus of resilience = = = 0.9 x 10-5 KN/mm2 Modulus of toughness = = = 0.006 KN/mm2 ( ) A tensile test was carried out on locally manufactured round steel bar 12 mm diameter. The percentage elongation measured over a gage length of 5d and 10d are 34% and 30% respectively. Another imported steel bar of the same diameter was tested and the elongation percent measured over a gage length of 4D was 37%. Calculate which one of those two steels is of superior ductility. Elongation equation: ∆L = bLо+c Aо Aо = π/4 (12)2 = 113 mm2 For local specimens % = b + 26 ∆L Lo c Aо Lo 34 100 c 113 5 x 12 30 100 c 113 10 x 12 ∆L Lo 0.45Aо Lo 0.45113 4 x 12
- 27. = b +(1) = b + (2) From 1 & 2 b = 0.26 c = 0.45 % = 0.26 + With local specimen with L = 4D Elong. % = 0.26 + = 36% The imported specimen with elong% of 37% is better than local specimen with elong % of 36% ( ) A bar of 5 m long is made up from two materials as shown in the figure. The first 1.7 m of its length is of brass and is 7.5 cm2 in cross section and the remainder of its length is of steel and 6 cm2 in cross section. Determine the load in kg required to produce a total elongation in the bar of 0.12 cm. Es = 2.1 x 106 kg/cm2 Eb = 1 x 106 kg/cm2 ΔL = ΔLs = = ΔLb = = 27 Brass Steel W 3.3m 1.7m 5m P L E A W Ls Es As W Lb Eb Ab 330 W 2.1x 106 x 6 170 W 1x 106 x 7.5 330 W 2.1x 106 x 6 170 W 1x 106 x 7.5
- 28. ΔLtot = ΔLs+ ΔLb = 0.12 + = 0.12 W = 2456 kg ( ) A 20 cm long steel tube 15 cm internal diameter and 1 cm thickness is surrounded closely by a brass tube of the same length and thickness. The tubes carry an axial load of 15 ton. Estimate the load carried by each tube. Steel Di = 15 Do = 17 Es = 2.1 x 106 kg/cm2 Brass Di = 17 Do = 19 Eb = 1 x 106 kg/cm2 ΔLs = ΔLb Ls = Lb = 28 20c m 151719 Ws Ls Es As W Lb Eb Ab Ws 2.1 x 106 x π/4(172 - 152 ) Wb 1 x 106 x π/4 (192 - 172 )
- 29. = Wb + Ws= 15 ton Ws = 9.77 ton Wb = 5.23 ton ( ) The tension test was carried out on mild steel specimen of 5 mm diameter and 20 cm gauge length. The gauge length was divided into 10 divisions. After rupture the lengths of those divisions were as follows: Division No. 1 2 3 4 5 6 7 8 9 10 Lf , mm 24 24 25 29 23.5 23.5 23 23 22.5 22.5 i) Illustrate the division which the rupture was occurred in ii) Draw the elongation distribution along the gage length iii) Draw the relation between the elongation and gage length iv) Determine the Unwin's constant (b&c) v) Draw the relation between the elongation % and the gage length Lo = 200 mm length of division = 20 mm Division No. 1 2 3 4 5 6 7 8 9 10 Lf , mm 24 24 25 29 23.5 23.5 23 23 22.5 22.5 ΔL = Lf - Lo 4 4 5 9 3.5 3.5 3 3 2.5 2.5 i) The division which the rupture was occurred in is no. 4 ii) 290 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 6 7 8 9 10 11 Elong. Division No.
- 30. iii) Gage length, L20 60 100 Elongation, ΔL 9 17.5 25 Elongation % 45 29 25 30 20 60 100 0 5 10 15 20 25 30 35 40 45 50 0 20 40 60 80 100 120 0 5 10 15 20 25 30 0 20 40 60 80 100 120 Elong. Elong. % Gauge length Gauge length
- 31. iv) Elongation equation: ∆L= bLо+c Aо Aо = π/4 (5)2 = 19.6 mm2 9 = 20b + c 19.6 (1) 25 = 100b + c 19.6 (2) b = 0.2 c = 1.13 ( ) In a tension test of a 8 mm diameter steel bar, which is divided into 10 divisions each of 20 mm length, fracture took place in forth division from one end of the bar. If the length of those division after rupture is given as follows: Division No. 1 2 3 4 5 6 7 8 9 10 Length after rupture , mm 24 24 25 29 23.5 23.5 23 23 22.5 22.5 i) Draw the elongation distribution along the specimen axis ii) Draw the relation of elongation versus gage length iii) Draw the relation of percent elongation versus gage length iv) Determine Unwin's constant Length of division = 20 mm Division No. 1 2 3 4 5 6 7 8 9 10 Lf , mm 24 24 25 29 23.5 23.5 23 23 22.5 22.5 ΔL = Lf - Lo 4 4 5 9 3.5 3.5 3 3 2.5 2.5 ii) 310 1 2 3 4 5 6 7 8 9 10 0 1 2 3 4 5 6 7 8 9 10 11 Elong. Division No.
- 32. iii) Gage length, L20 60 100 Elongation, ΔL 9 17.5 25 Elongation % 45 29 25 32 20 60 100 0 5 10 15 20 25 30 35 40 45 50 0 20 40 60 80 100 120 0 5 10 15 20 25 30 0 20 40 60 80 100 120 Elong. Elong. % Gauge length Gauge length
- 33. Pmax Aо 66.7 64.6 ∆Lf Lо 5.6x 100 50 Ao – Af Aо 64.6–52.6 64.6 iv)Elongation equation: ∆L = bLо+c Aо Aо = π/4 (8)2 = 50.3 mm2 9 = 20b + c 50.3 (1) 25 = 100b + c 50.3 (2) b = 0.4 c = 0.7 ( ) In tension test on hot rolled AISI 1095 steel, the original diameter was 9.07 mm, and the original gage length for longitudinal strain was 50 mm. The highest load observed was 66.7 KN, and at this point the gage length had increased to 54.2 mm. At fracture into two pieces, which occurred at a load of 63.4 KN, the broken halves were fitted back together, and the diameter was measured to be 8.18 mm. Also, the gage length had increased to 55.6 mm. Calculate the following: (a) Engineering ultimate strength, (b) Percent elongation at fracture, and (c) percent reduction in area at fracture. Max. Failure P (KN) 66.7 63.4 ∆L (mm( 54.2 – 50 = 4.2 mm 55.6 – 50 = 5.6 mm D(mm) 8.18 mm Lо = 50 mm Aо = π/4 (9.07)2 = 64.6 mm2 (a) Ultimate strength σmax = = = 1.033 KN/mm2 (b) Elongation % = % = = 11.2% 33
- 34. Af = π/4(8.18)2 = 52.6 mm2 (b) % reduction in area = % = = 18.6% 34