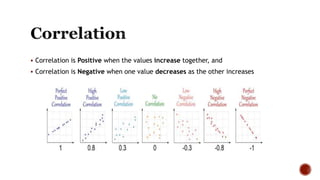
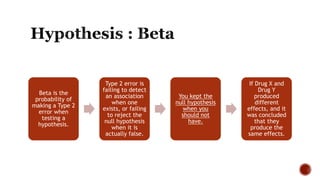
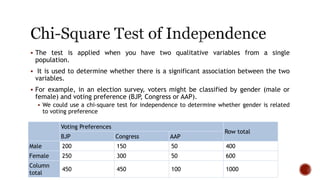
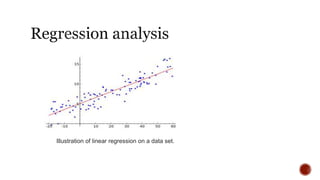
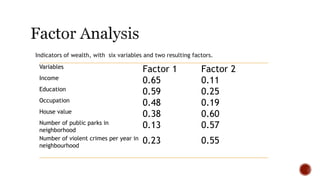
The document discusses various statistical tools utilized in research, focusing on key concepts such as correlation, hypothesis testing, chi-square tests, regression analysis, and factor analysis. It details the definitions and applications of these statistical methods, including examples and the importance of distinguishing between correlation and causation. Additionally, it addresses the concepts of null and alternative hypotheses along with the significance levels (alpha and beta errors) in hypothesis testing.

1. Statistical Tools used in Research
Submitted to:
Dr. Bhagwan Singh
Submitted By:
Subhrat Sharma
CUHP13MBA85
Central University of Himachal Pradesh

2. Statistics Defined Correlation Hypothesis
• Hypothesis :
Alpha
• Hypothesis :
Beta
Chi-Square Test of
Independence
Regression
analysis
Factor Analysis References

3. Statistics is the science and practice of developing human knowledge through the use of
empirical data expressed in quantitative form. It is based on statistical theory which is a branch
of applied mathematics. Within statistical theory, randomness and uncertainty are modelled by
probability theory. (Wikipedia Encyclopaedia)
What is statistics?
 The collecting, summarizing, and analysing of data.
 The term also refers to raw numbers, or “stats”, and to the summarization of data.
Example: Frequencies

4. Allows an examination of the relationship between variables; is there a relationship between
these variables? Are they positively or negatively related?
A correlation coefficient of 0 means that there is no relationship between the variables, -1
negative relationship, 1 positive relationship.
Important: Correlation is not causation.
•"Correlation Is Not Causation" ... which says that a correlation does not mean that one thing causes the other (there
could be other reasons the data has a good correlation).
Ex. What is the relationship between exercise and depression?
•Does depression increase when exercise increases?
•Does depression decrease when exercise increases?
•Is there no significant correlation between exercise and depression?

5.  Correlation is Positive when the values increase together, and
 Correlation is Negative when one value decreases as the other increases

6. Null hypothesis: A hypothesis put forward to argue that a relationship or pattern does not exist.
•Cholesterol study example: In a Randomized Control Trial, the control group and the treatment group have equal
levels of cholesterol at the end of a study.
•Null hypothesis: Groups A and B are equal.
•Denoted by Ho:
Alternative Hypothesis: Statement of what study is set to establish.
•Alternative Hypothesis: Groups A and B have different levels of cholesterol.
•Denoted by H1:
The null hypothesis will be true if the findings are insignificant.
The null hypothesis will be false if the findings are significant.

7. Alpha level, or significance level, is the value that is determined by the researcher in order to reject or retain the
null hypothesis. It is a pre-determined value, not calculated.
• In other words, if we select a value of .05, findings would be deemed statistically significant if they were
found to be .05 or less.
What does this mean?
• Alpha indicates the probability that the null hypothesis will be rejected when it is true (in other
words, the null hypothesis is wrongly rejected).
This is called Type 1 error or alpha error
E.g. in a trial of new Drug X, the null hypothesis might be that the new Drug X is no better
than the current Drug Y.
• H0: there is no difference between Drug X and Drug Y.
• A Type 1 error would occur if we concluded that the two drugs
• produced different effects when there was no difference between them.

8. Beta is the
probability of
making a Type 2
error when
testing a
hypothesis.
Type 2 error is
failing to detect
an association
when one
exists, or failing
to reject the
null hypothesis
when it is
actually false.
You kept the
null hypothesis
when you
should not
have.
If Drug X and
Drug Y
produced
different
effects, and it
was concluded
that they
produce the
same effects.

9.  The test is applied when you have two qualitative variables from a single
population.
 It is used to determine whether there is a significant association between the two
variables.
 For example, in an election survey, voters might be classified by gender (male or
female) and voting preference (BJP, Congress or AAP).
 We could use a chi-square test for independence to determine whether gender is related
to voting preference
Voting Preferences
Row total
BJP Congress AAP
Male 200 150 50 400
Female 250 300 50 600
Column
total
450 450 100 1000

10. When to Use Chi-Square Test for Independence
• The test procedure described in this lesson is appropriate when the
following conditions are met:
• The sampling method is simple random sampling.
• Each population is at least 10 times as large as its respective
sample.
• The variables under study are each categorical.
• If sample data are displayed in a contingency table, the expected
frequency count for each cell of the table is at least 5.

11. Regression analysis is used when you want to predict a continuous dependent variable from a number
of independent variables.
Regression analysis is widely used for prediction and forecasting.
Classical assumptions for regression analysis include:
• The sample is representative of the population for the inference prediction.
• The error is a random variable with a mean of zero conditional on the explanatory variables.
• The independent variables are measured with no error.
• The predictors are linearly independent, i.e. it is not possible to express any predictor as a linear combination of the others.
• The errors are uncorrelated, that is, the variance–covariance matrix of the errors is diagonal and each non-zero element is the
variance of the error.
• The variance of the error is constant across observations (homoscedasticity). If not, weighted least squares or other methods
might instead be used.

12. Illustration of linear regression on a data set.

13. Factor analysis is a
useful tool for
investigating variable
relationships for
complex concepts such
as socioeconomic status,
dietary patterns, or
psychological scales.
It allows researchers to
investigate concepts
that are not easily
measured directly by
collapsing a large
number of variables into
a few interpretable
underlying factors.
What is a factor?
• The key concept of factor
analysis is that multiple
observed variables have similar
patterns of responses because
they are all associated with a
latent (i.e. not directly
measured) variable.
• For example, people may
respond similarly to questions
about income, education, and
occupation, which are all
associated with the latent
variable socioeconomic status.

14. Variables
Factor 1 Factor 2
Income
0.65 0.11
Education
0.59 0.25
Occupation
0.48 0.19
House value
0.38 0.60
Number of public parks in
neighborhood
0.13 0.57
Number of violent crimes per year in
neighbourhood
0.23 0.55
Indicators of wealth, with six variables and two resulting factors.

15. • The variable with the strongest association to the underlying latent variable. Factor
1, is income, with a factor loading of 0.65.
• Since factor loadings can be interpreted like standardized regression coefficients,
one could also say that the variable income has a correlation of 0.65 with Factor 1.
This would be considered a strong association for a factor analysis in most research
fields.
• Two other variables, education and occupation, are also associated with Factor 1.
Based on the variables loading highly onto Factor 1, we could call it “Individual
socioeconomic status.”
• Notice that the variable house value also is marginally important in Factor 1
(loading = 0.38). This makes sense, since the value of a person’s house should be
associated with his or her income.

16.  http://dss.princeton.edu/online_help/analysis/regression_intro.htm
 http://stattrek.com/chi-square-test/independence.aspx
 http://www.statsoft.com/Textbook/Principal-Components-Factor-Analysis
 http://www.theanalysisfactor.com/factor-analysis-1-introduction/
 http://mathworld.wolfram.com/HypothesisTesting.html
 https://www.mathsisfun.com/data/correlation.html