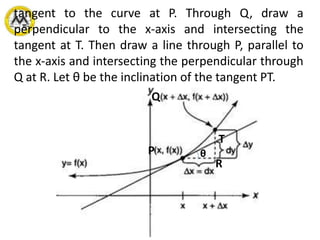
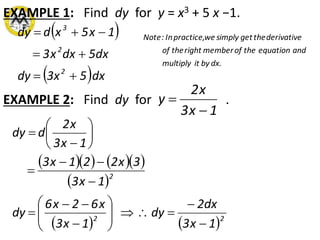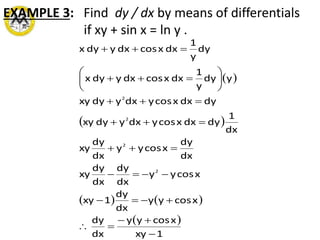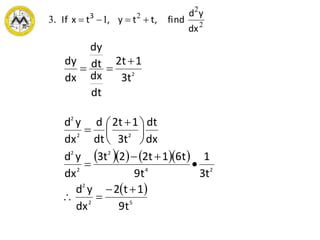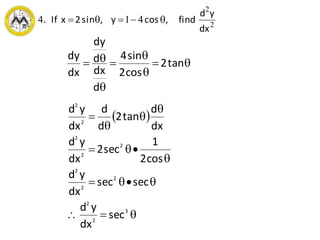This document discusses differentials and how they relate to differentiable functions. Some key points: 1. The differential of an independent variable x is defined as dx, which is equal to the increment Δx. The differential of a dependent variable y is defined as dy = f'(x) dx, where f'(x) is the derivative of the function. 2. Differentials allow approximations of changes in a function using derivatives, such as estimating errors or finding approximate roots. 3. Rules are provided for finding differentials of common functions using differentiation formulas. Examples demonstrate using differentials to estimate changes and approximate values.

1. The Differentials

2. Objectives
At the end of the lesson, the student should be able
to:
1. Compare the value of the differential, dy, with
the actual change in y,∆𝑦
2. Estimate a propagated error using a differential.
3. Find the approximate value of roots by using
differentials.
4. Find the differential of a function using
differentiation formulas.

3. Consider a function defined by y=f(x) where x is
the independent variable. In the four-step rule we
introduced the symbol Δx to denote the increment of
x. Now we introduce the symbol dx which we call the
differential of x. Similarly, we shall call the symbol dy
as the differential of y. To give separate meanings to
dx and dy, we shall adopt the following definitions of
a function defined by the equation y=f(x).
DEFINITION 1: dx = Δx
In words, the differential of the independent
variable is equal to the increment of the variable.

4. DEFINITION 2: dy = f’ (x) dx
In words, the differential of a function is equal to
its derivative multiplied by the differential of its
independent variable.
We emphasize that the differential dx is also an
independent variable, it may be assigned any value
whatsoever. Therefore, from DEFINITION 2, we see
that the differential dy is a function of two
independent variables x and dx. It should also be
noted that while dx=Δx, dy≠Δy in general.
Suppose dx≠0 and we divide both sides of the
equation
dy = f’ (x) dx

5. by dx. Then we get
 x'f
dx
dy

Note that this time dy/dx denotes the quotient of
two differentials, dy and dx . Thus the definition of
the differential makes it possible to define the
derivative of the function as the ratio of two
differentials. That is,
 
xofaldifferentithe
yofaldifferentithe
dx
dy
x'f 
The differential may be given a geometric
interpretation. Consider again the equation y=f(x)
and let its graph be as shown below. Let P(x,y) and
Q(x+Δx,f(x)+Δx) be two points on the curve. Draw the

6. tangent to the curve at P. Through Q, draw a
perpendicular to the x-axis and intersecting the
tangent at T. Then draw a line through P, parallel to
the x-axis and intersecting the perpendicular through
Q at R. Let θ be the inclination of the tangent PT.
P
Q
T
R
θ

7. From Analytic Geometry, we know that
slope of PT = tan θ
But triangle PRT, we see that
x
RT
PR
RT
tan

 
However, Δx=dx by DEFINITION 1 . Hence
dx
RT
tan 
But the derivative of y=f(x) at point P is equal to the
slope of the tangent line at that same point P.
slope of PT = f’(x)
Hence,
 
dx
RT
x'f 

8. And , RT = f’(x) dx
But, dy = f’ (x) dx
Hence, RT = dy
We see that dy is the increment of the ordinate of
the tangent line corresponding to an increment in Δx
in x whereas Δy is the corresponding increment of
the curve for the same increment in x. We also note
that the derivative dy/dx or f’(x) gives the slope of
the tangent while the differential dy gives the rise of
the tangent line.

9. SUMMARY:
DEFINITION OF DIFFERENTIALS
• Let x represents a function that is differentiable
on an open interval containing x. The
differential of x (denoted by dx) is any nonzero
real number.
• The differential of y (denoted by dy) is
dy = f(x )dx.

10. DIFFERENTIAL FORMULAS
Let u and v and be differentiable functions of x.
• Constant multiple: d(cu)= c du
• Sum or difference: d[u±v] =du±dv
• Product: d[uv]=udv+vdu
• Quotient: d
𝒖
𝒗
=
𝒗𝒅𝒖−𝒖𝒅𝒗
𝒗 𝟐

11. EXAMPLE 1: Find dy for y = x3 + 5 x −1.
 
 dx53xdy
dx5dxx3
1x5xddy
2
2
3



EXAMPLE 2: Find dy for .
1x3
x2
y


     
 
   22
2
1x3
2dx
dy
1x3
x62x6
dy
1x3
3x221x3
1x3
x2
ddy






















dx.byitmultiply
andequationtheofmemberrighttheof
derivativethegetsimplywepractice,In:Note

12. EXAMPLE 3: Find dy / dx by means of differentials
if xy + sin x = ln y .
 
 
   
 
1xy
xcosyy
dx
dy
xcosyy
dx
dy
1xy
xcosyy
dx
dy
dx
dy
xy
dx
dy
xcosyy
dx
dy
xy
dx
1
dydxxcosydxydyxy
dydxxcosydxydyxy
ydy
y
1
dxxcosdxydyx
dy
y
1
dxxcosdxydyx
2
2
2
2

















13. EXAMPLE 1: Use differentials to approximate the change
in the area of a square if the length of its side increases
from 6 cm to 6.23 cm.
Let x = length of the side of the square.
The area may be expressed as a function of x,
where A= x2.
The differential dA is   dxx2dAdxx'fdA 
Because x is increasing from 6 to 6.23, you find that
Δ x = dx = .23 cm; hence,   
2
cm76.2dA
cm23.0cm62dA


  .cm2.8129isyareainincrease
exactthethatNote6.23.to6fromincreaseslengthsideitsas
cm2.76elyapproximatbyincreasewillsquaretheofareaThe
2
2


14. EXAMPLE 2: Use the local linear approximation to estimate
the value of to the nearest thousandth.3
55.26
 
   
 
 
2.9830.0167-355.26
60
1
355.26therefore;327thatless
60
1
telyapproximabewill55.26thatimplieswhich
0167.0
60
1
100
45
27
1
45.0
273
1
dy,Hence
0.45dxxthen26.55,to27fromdecreasingisxBecause
dx
x3
1
dxx
3
1
dy
xxfdxxf'dy
isdyaldifferentiThe27.x
namely26.55,tocloserelativelyisandcubeperfectaisthatxofvalue
convenientachoose,xxfisapplyingareyoufunctiontheBecause
3
33
3
3
2
3
2
3
2
3
1
3










15. EXAMPLE 3: If y = x3 + 2x2 – 3, find the approximate value
of y when x = 2.01.
2.xofvalueoriginalanto0.01dxxof
incrementanapplyingofresulttheas2.01gconsiderin
arewethen0.01,22.01writeweifthatNotedy.y
forsolveshallwethenvalue,eapproximatthefindto
askedsimplyarewesincebutyyisvalueexactThe



 
  
20.1320.013dyy
isionapproximatrequiredthe,therefore
20.001.0812dy
then,01.0dxand2xwhenand
13388ythen,2xwhen
dxx4x3dythen
3x2xySince
2
23







16. EXAMPLE 4: Use an appropriate local linear approximation
to estimate the value of cos 310.
 
 
 
 
  
  8573.0008725.0866.0dyy
isionapproximatrequiredthe,therefore
008725.001745.05.0dy
180
130sindy
then,01745.0
180
1dxand30xwhenand
866.030cosythen,30xwhen
dxxsindythen
xcosyLet
0
00
0
00
00







 






 





17. Derivative of Parametric Equations
• The first derivative of the parametric
equations y=f(u) and x=g(u) with respect to
x is equal to the ratio of the first derivative of
y with respect u divided by the derivative of x
with respect to u, i.e.
𝒅𝒚
𝒅𝒙
=
𝒅𝒚
𝒅𝒖
𝒅𝒙
𝒅𝒖
=
𝒇′(𝒖)
𝒈′(𝒖)
, 𝒈′(𝒖) ≠ 𝟎

18. • The second derivative
𝑑2 𝑦
𝑑𝑥2 of the equations in
parametric form is
𝑑2
𝑦
𝑑𝑥2
=
𝑑
𝑑𝑢
𝑑𝑦
𝑑𝑥
∙
𝑑𝑢
𝑑𝑥
=
𝑑𝑦′
𝑑𝑢
∙
𝑑𝑢
𝑑𝑥

19. Find the derivatives of the following parametric
equations :
3tcot
3sin3t-
3cos3t
dt
dx
dt
dy
dx
dy
tcos
dt
dy
andtsin
dt
dx
:Solution
3tsiny3t,cosx.



3333
1
EXAMPLE :

20.  
 
tsintsin
tcostcos
tsintsin
tcostcos
tsintsin
tcostcos
dt
dx
dt
dy
dx
dy
tcostcos
dt
dy
andtsintsin
dt
dx
:Solution
5sin4t-t8siny5cos4t,8costx.
452
452
4524
4524
4208
4208
4208
4208
2













21. 2
2
2
13
dx
yd
find,tty,txIf. 3

2
t3
1t2
dt
dx
dt
dy
dx
dy 

     
 
52
2
24
2
2
2
22
2
t9
1t2
dx
yd
t3
1
t9
t61t22t3
dx
yd
dx
dt
t3
1t2
dt
d
dx
yd










 


22. 2
2
414
dx
yd
find,cosy,sin2xIf. 





 tan2
cos2
sin4
d
dx
d
dy
dx
dy
 








3
2
2
2
2
2
2
2
2
2
2
sec
dx
yd
secsec
dx
yd
cos2
1
sec2
dx
yd
dx
d
tan2
d
d
dx
yd

23.  
 .0,4attyandttx
:curveparametricthetoslinetangenttheFind.
25
 3
4
5
   125tt
2
125tt
2t
t125t
2t
dt
dx
dt
dy
dx
dy
line.tangenttheofslopethegetcanwe
thatso,
dx
dy
findandderivativethefindtohaveWe
22224







24.  
 
  
 
  
 
4x
8
1
yx
8
1
4-yislinetangentsecondofequationthethus
8
1
mis0,4atlinetangenttheofslopetheTherefore
8
1
12252
2
dx
dy
,2tat,Now
4x
8
1
yx
8
1
4-yislinetangentofequationthethus
8
1
mis0,4atlinetangenttheofslopetheTherefore
8
1
12252
2
dx
dy
2,tat
definednotis
dx
dy
0,tat
2t0,t
04t,0t
04ttt4t0
becomescurvetheofequationcparametrithe4,0at,Now
2
2
23
2335















25. Other Examples:
• Use differentials to approximate the value of
the following expression.
• Find the differential dy of the given function.

26. Find the first and second derivative of y with
respect to x from the given parametric equations.
1. 𝑥 = 2 + 𝑠𝑒𝑐𝜃, 𝑦 = 1 + 2𝑡𝑎𝑛𝜃
2. 𝑥 = 𝑐𝑜𝑠3
𝜃, 𝑦 = 𝑠𝑖𝑛3
𝜃
3. 𝑥 = (𝑡 − 2)
3
2, 𝑦 = 𝑡2
− 1
4. 𝑥 = 𝑡 + 𝑡−1
, 𝑦 = 𝑡2
+ 𝑡−2
5. 𝑥 =
𝑢
1+𝑢3 , 𝑦 =
𝑢2
1+𝑢3

27. Differential of Arc Length
Let y=f(x)be a continuous function. Let P(x,y)
and Q(𝑥 + ∆𝑥, 𝑦 + ∆𝑦)be on the curve of f(x).
Denote ∆𝑠 be the arc length from P to Q. The
rate of the arc s from P to Q per unit change in
x and the rate of change per unit change in y
are given by
𝑑𝑠
𝑑𝑥
= lim
∆𝑥→0
∆𝑠
∆𝑥
= 1 +
𝑑𝑦
𝑑𝑥
2
𝑑𝑠
𝑑𝑦
= lim
∆𝑥→0
∆𝑠
∆𝑥
= 1 +
𝑑𝑥
𝑑𝑦
2

28. 𝑄(𝑥 + ∆𝑥, 𝑦 + ∆𝑦)
∆𝑠
∆𝑦
P(x,y)
∆𝑥
When the curve is given in parametric equations 𝑥 =
𝑓 𝑡 𝑎𝑛𝑑 𝑦 = 𝑔(𝑡), the rate of change of s with
respect to time t is given by
𝒅𝒔
𝒅𝒕
=
𝒅𝒙
𝒅𝒕
𝟐
+
𝒅𝒚
𝒅𝒕
𝟐

29. Curvature
The curvature K (the measure of how sharply a curve
bends) of a curve y=f(x), at any point P on it is the rate of
change in direction, i.e. the angle of inclination 𝜶 of the
tangent line at P per unit of arc length s.
K= lim
∆𝒔→𝒐
∆𝜶
∆𝒔
=
𝒅𝒔
𝒅𝜶
=curvature at P
𝜶 + ∆𝜶
∆𝒔
∆𝜶

30. The curvature at a point P of the curve y=f(x) is
𝐾 =
𝑦′′
1 + (𝑦′)2
3
2
When the equation of the curve is given in
parametric form x=f(u) and y=g(u)
𝐾 =
𝑓′
𝑔′′
− 𝑓′′
𝑔′
(𝑓′)2 + (𝑔′)2
3
2

31. Radius of Curvature
Consider the curve y=f(x) having the tangent line
L at P and curvature K. Consider a circle which
lies on the side of the curve and tangent to line L
at P with curvature K. this is called the circle of
curvature with radius of curvature R defined to
R=
1
𝐾
=
1+(𝑦′)2
3
2
𝑦′′

32. K
L
P
y
XO

33. Example
Find the curvature and radius of curvature of the
plane curve at the given value of x.
1. 𝑦 = 3𝑥 − 2, 𝑥 = 𝑎
2. 𝑦 = 2𝑥2
+ 3, 𝑥 = −1
3. 𝑦 =
2
3
16 − 𝑥2 , x = 0
4. 𝑦 = 𝑐𝑜𝑠2𝑥, 𝑥 = 2𝜋
5. X=sin𝜃, 𝑦 = 𝑠𝑖𝑛2𝜃, 𝜃 =
𝜋
2