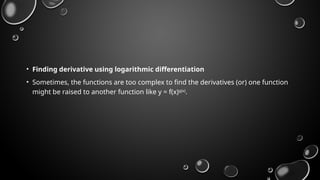
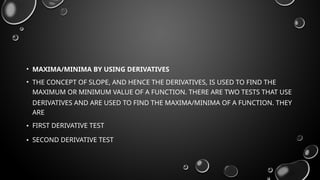
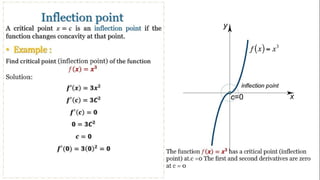
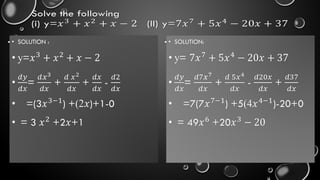
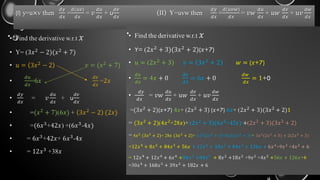
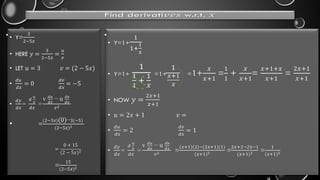
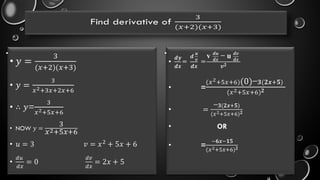
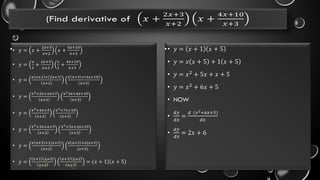
The document outlines the fundamental concepts of derivatives, including their definition, rules of differentiation such as the power rule, product rule, and quotient rule, and their applications in optimizing functions and analyzing rates of change. It also covers higher-order derivatives, partial derivatives, and methods for finding maxima and minima using the first and second derivative tests. Additionally, it emphasizes the practical applications of derivatives in real-life scenarios like displacement and motion problems.

1. Derivatives
WEIGHTAGE : 25% MARKS

2. The derivative of a function is the rate of change of the function's output
relative to its input value. Given y = f(x),
the derivative of f(x), denoted f'(x) or , is
defined by the following limit:

3. • The derivative of a function f(x) in math is denoted by f'(x) and can be contextually
interpreted as follows:
• The derivative of a function at a point is the slope of the tangent drawn to that
curve at that point.
• It also represents the rate of change at a point on the function.
• The velocity of a particle is found by finding the derivative of the displacement
function.
• The derivatives are used to optimize (maximize/minimize) a function.
• They are also used to find the intervals where the function
is increasing/decreasing as well as the intervals where the function is concave
up/down.

4. • Power rule: by this rule, if y=f(x) = xn
, then = n x n-1
.
• example: = 5x4
.
• Sum/difference rule: the derivative process can be
distributed over addition/subtraction. I.E= .
• Product rule: the product rule of derivatives states that if a
function is a product of two functions, then its derivative is
the derivative of the second function multiplied by the first
function added to the derivative of the first function
multiplied by the second function.

5. • QUOTIENT RULE: THE QUOTIENT RULE OF DERIVATIVES STATES THAT D/DX (U/V) =
(V · DU/DX - U · DV/DX)/ V2
• CONSTANT MULTIPLE RULE: THE CONSTANT MULTIPLE RULE OF DERIVATIVES
STATES THAT D/DX [C(F(X)] = C · D/DX F(X). I.E., THE CONSTANT WHICH WHEN
MULTIPLIED BY A FUNCTION, COMES OUT OF THE DIFFERENTIATION PROCESS.
FOR EXAMPLE, D/DX (5X2
) = 5 D/DX (X2
) = 5(2X) = 10 X.
• CONSTANT RULE: THE CONSTANT RULE OF DERIVATIVES STATES THAT THE
DERIVATIVE OF ANY CONSTANT IS 0. IF Y = K, WHERE K IS A CONSTANT, THEN DY/DX
= 0. SUPPOSE Y = 4, Y' = 0. THIS RULE DIRECTLY FOLLOWS FROM THE POWER RULE.

6. • If f and g are differentiable functions in their domain, then f(g(x)) is also
differentiable. This is known as the chain rule of differentiation used for
composite functions.
• DERIVATIVES OF IMPLICIT FUNCTIONS
• IN EQUATIONS WHERE Y AS A FUNCTION OF X CANNOT BE EXPLICITLY DEFINED BY
THE VARIABLES X AND Y, WE USE IMPLICIT DIFFERENTIATION. IF F(X, Y) = 0, THEN
DIFFERENTIATE ON BOTH SIDES WITH RESPECT TO X AND GROUP THE TERMS
CONTAINING DY/DX AT ONE SIDE, AND THEN SOLVE FOR DY/DX.

7. • PARAMETRIC DERIVATIVES
• IN A FUNCTION, WE MAY HAVE THE DEPENDENT VARIABLES X AND Y WHICH ARE
DEPENDENT ON THE THIRD INDEPENDENT VARIABLE. IF X = F(T) AND Y = G(T),
THEN DERIVATIVE IS CALCULATED AS DY/DX = F'(X)/G'(X). SUPPOSE, IF X = 4 + T2
AND
Y = 4T2
-5T4

8. • HIGHER-ORDER DERIVATIVES
• WE CAN FIND THE SUCCESSIVE DERIVATIVES OF A FUNCTION AND OBTAIN THE
HIGHER-ORDER DERIVATIVES. IF Y IS A FUNCTION, THEN ITS FIRST DERIVATIVE IS
DY/DX. THE SECOND DERIVATIVE IS D/DX (DY/DX) WHICH ALSO CAN BE WRITTEN
AS D2
Y/DX2
. THE THIRD DERIVATIVE IS D/DX (D2
Y/DX2
) AND IS DENOTED BY
D3
Y/DX3
AND SO ON.

9. • PARTIAL DERIVATIVES
• IF U = F(X,Y) WE CAN FIND THE PARTIAL DERIVATIVE OF WITH RESPECT TO Y BY
KEEPING X AS THE CONSTANT OR WE CAN FIND THE PARTIAL DERIVATIVE WITH
RESPECT TO X BY KEEPING Y AS THE CONSTANT. SUPPOSE F(X, Y) = X3
Y2
, THE
PARTIAL DERIVATIVES OF THE FUNCTION ARE:
• ∂F/ X(X
∂ 3
Y2
) = 3X2
Y AND
• ∂F/ Y(X
∂ 3
Y2
) = X3
2Y

10. • Finding derivative using logarithmic differentiation
• Sometimes, the functions are too complex to find the derivatives (or) one function
might be raised to another function like y = f(x)g(x)
.

11. • MAXIMA/MINIMA BY USING DERIVATIVES
• THE CONCEPT OF SLOPE, AND HENCE THE DERIVATIVES, IS USED TO FIND THE
MAXIMUM OR MINIMUM VALUE OF A FUNCTION. THERE ARE TWO TESTS THAT USE
DERIVATIVES AND ARE USED TO FIND THE MAXIMA/MINIMA OF A FUNCTION. THEY
ARE
• FIRST DERIVATIVE TEST
• SECOND DERIVATIVE TEST

12. • First derivative test
• We can just use the first derivative to determine the maximum or minimum by
observing the following points:
• F'(x) represents the slope of a tangent line.
• Hence, if f'(x) > 0, the function is increasing, and if f'(x) < 0, the function is decreasing.
• If f'(x) > 0 is changing to f'(x) < 0 at a point, then the function has a local maximum at
that point.
• If f'(x) < 0 is changing to f'(x) > 0 at a point, then the function has a minimum at that
point.
• Note that f'(x) = 0 at local maximum and local minimum.

13. • Second derivative test
• The second derivative test uses the critical points and the second derivative to find
the maxima/minima. To perform this test:
• Find the critical points by setting f'(x) = 0.
• Substitute each of these in f''(x). If f''(x) < 0, then the function is maximum at that
point and if f''(x)>0, then the function is minimum at that point.
• If f''(x) = 0, the function neither has maxima nor minima at that point, and in this
case, it is known as the point of inflection.

15. • There are various applications of derivatives in real life.
• The rate of change of a function with respect to another quantity is the derivative.
• To check if a function is increasing or decreasing.
• To find the equation of the tangent/normal.
• To find the maximum and minimum values from a graph.
• To find the displacement-motion problems.
• To find velocity given displacement, to find the acceleration given displacement.

16. USING DEFINITION OBTAIN DERIVATIVE
• = lim
ℎ→0
𝑥+ℎ−𝑥
ℎ (ξ𝑥+ℎ+ξ𝑥)
= lim
ℎ→0
ℎ
ℎ (ξ𝑥+ℎ+ξ𝑥)
= lim
ℎ→0
1
(ξ𝑥+ ℎ+ ξ𝑥)
=
1
(ξ𝑥+0+ξ𝑥)
=
1
(ξ𝑥+ ξ𝑥)
=
1
2ξ𝑥

17. DERIVATIVE OF CONSTANT ( C )
•

18. Using definition find derivatives
• •

19. Using definition find derivatives
• •

20. IMPORTANT FORMULAE FOR DIFFERENTIATION
•

21. RULES OF DERIVATIVES
•

22. (III) 5X-9

23. • •

24. • •

25. NOW TRY YOUR SELF
•

26. • •

27. • •

28. • •

29. • •

30. • •

31. • •

32. • •

33. • •

34. • •

35. •