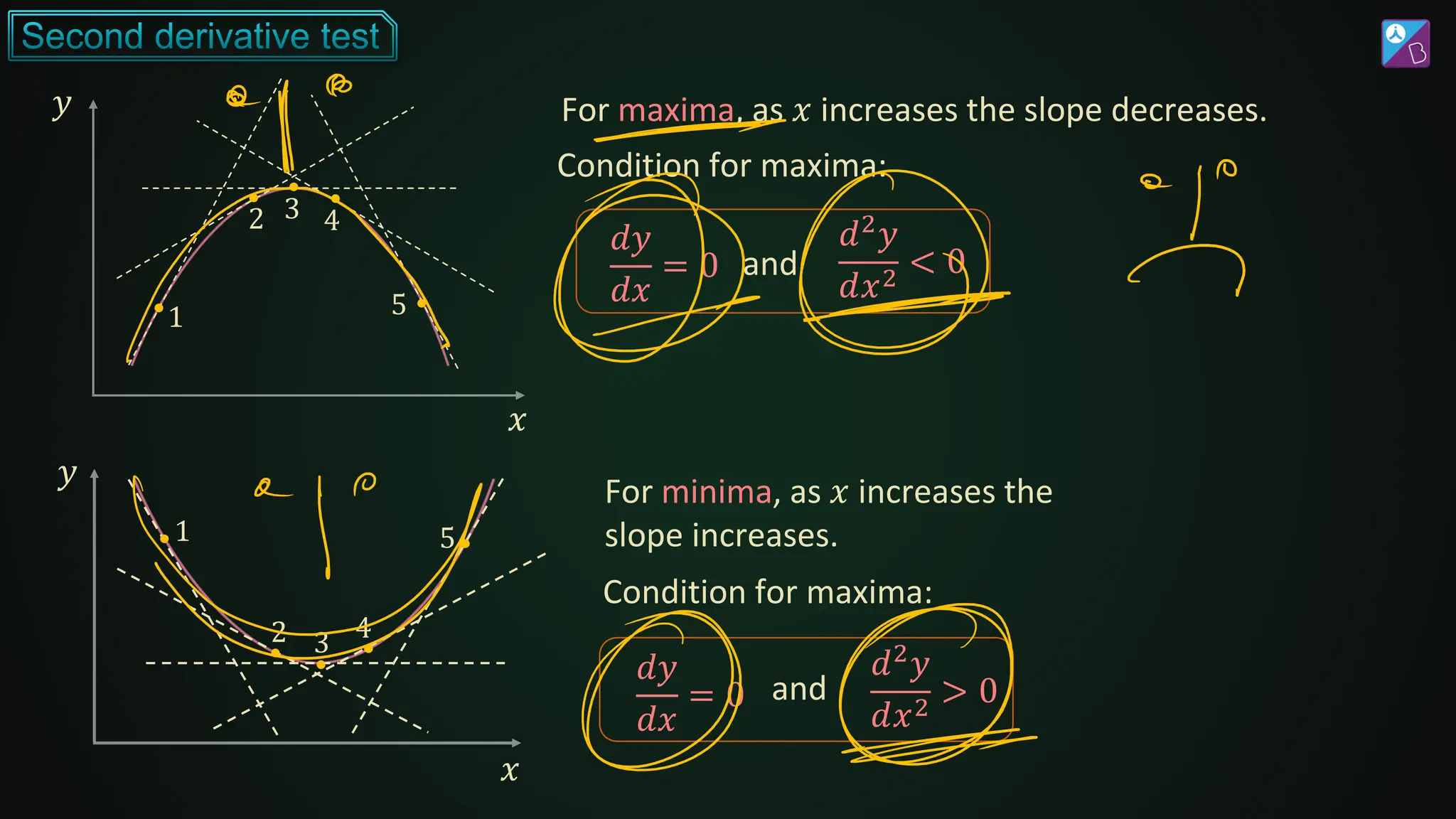
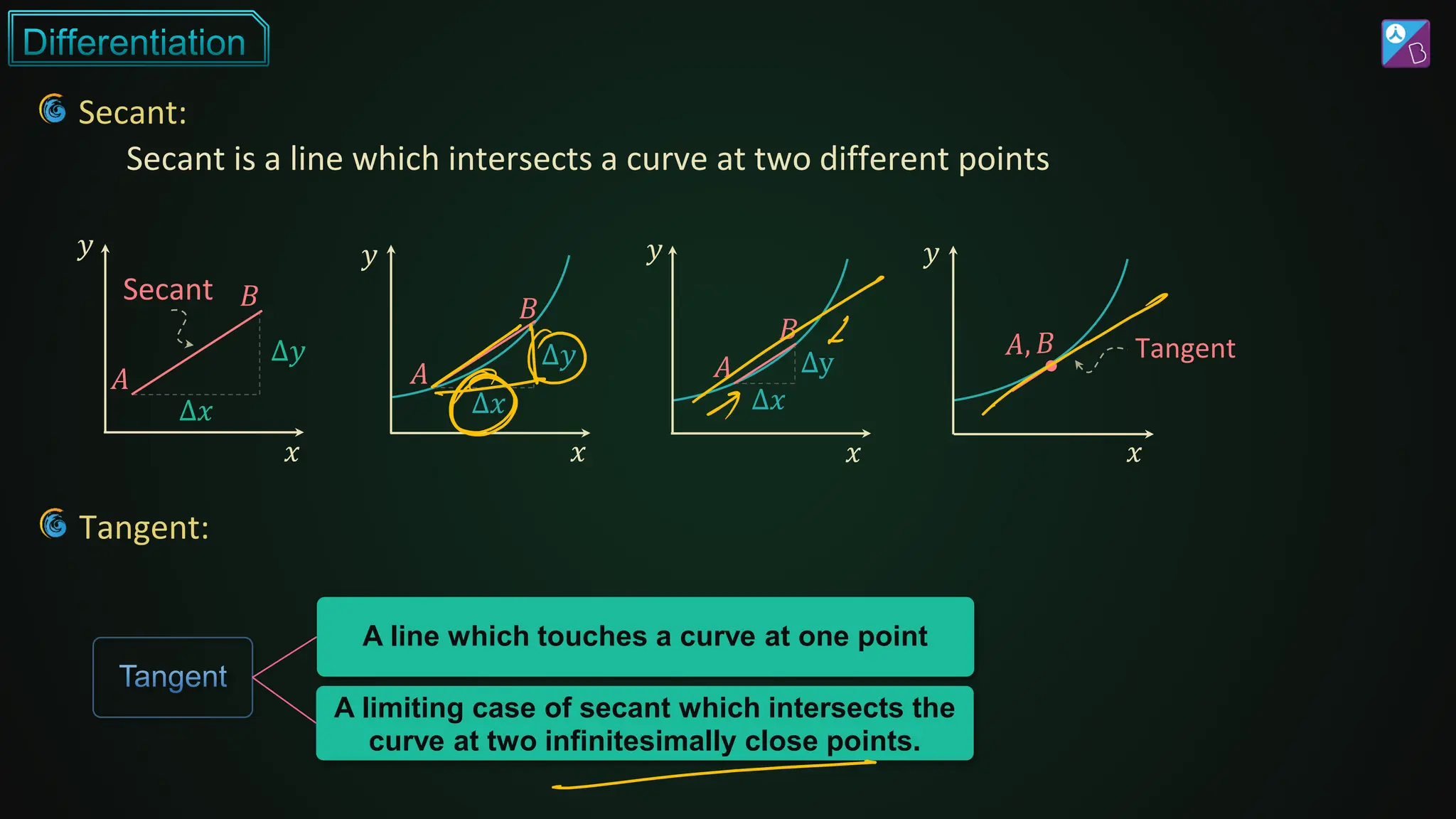
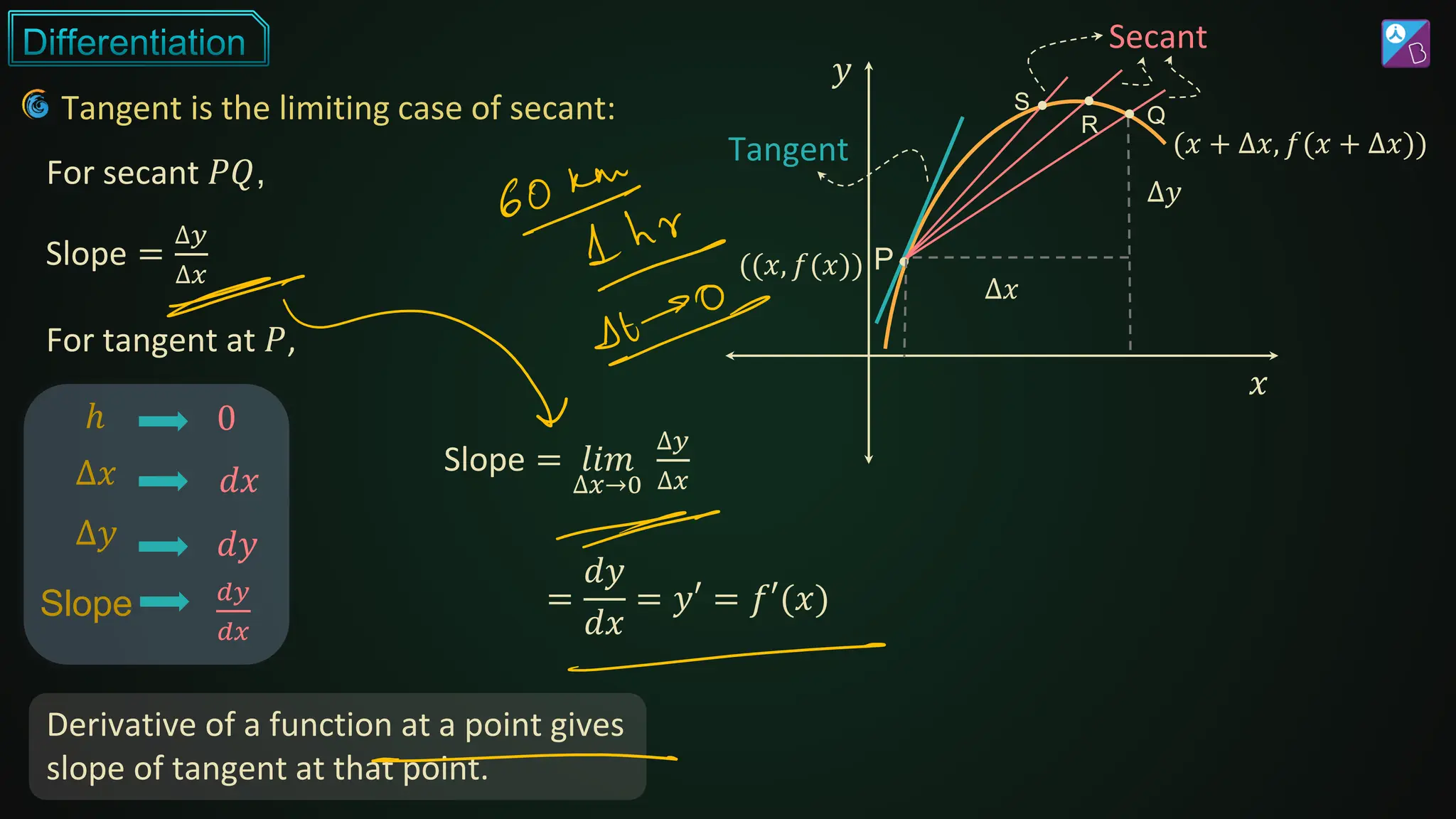
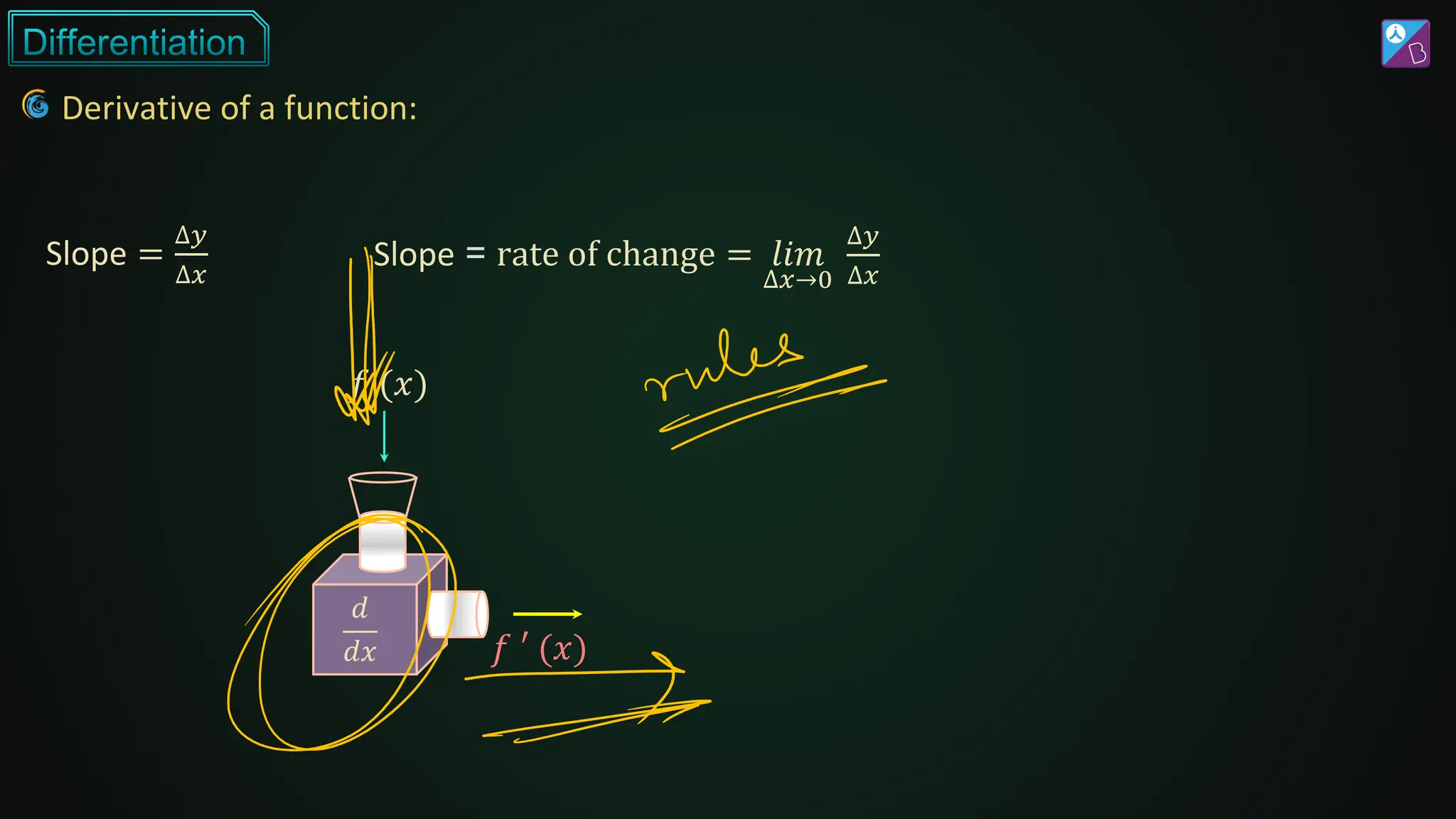
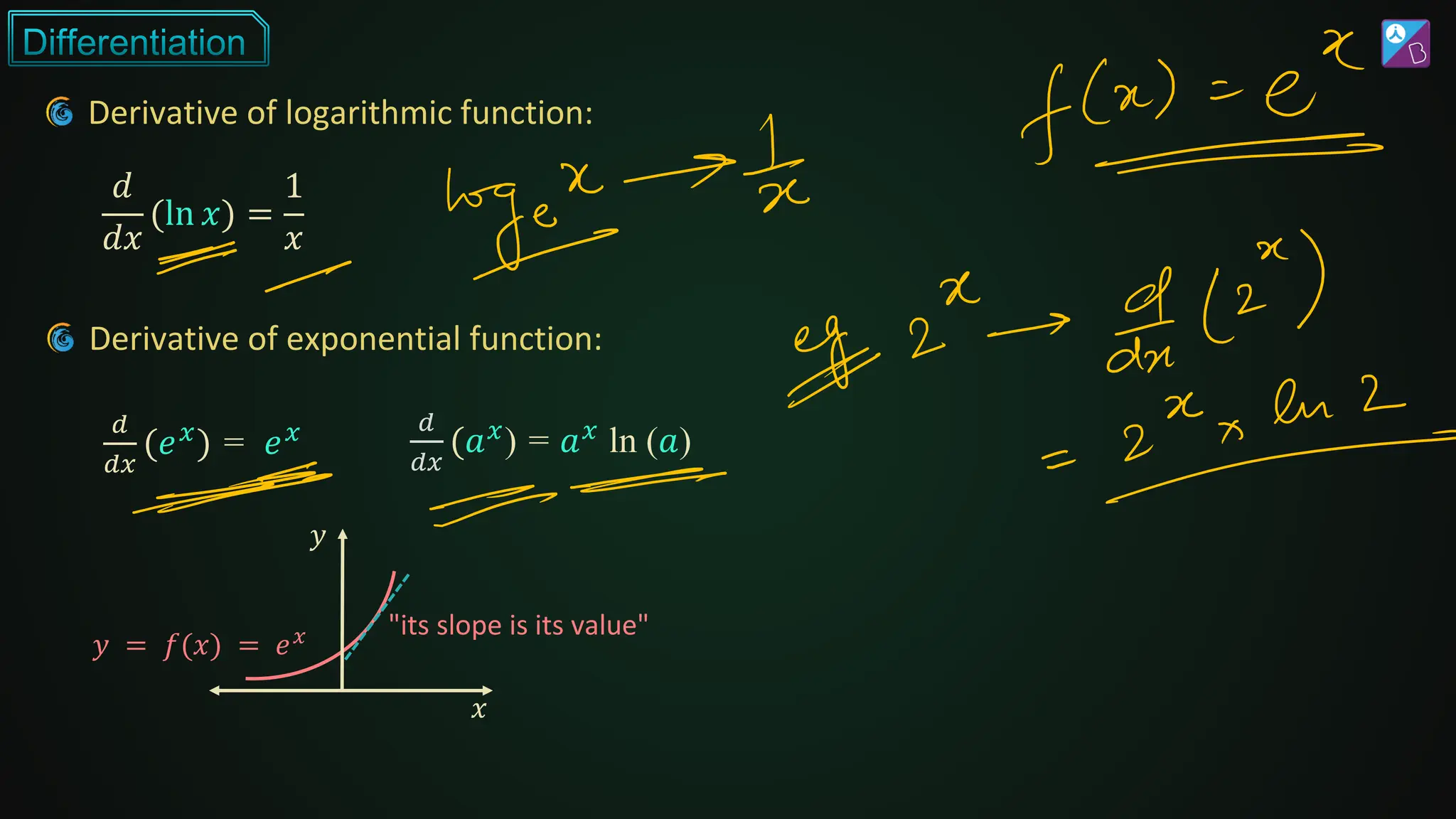
The document discusses differentiation, covering its fundamental concepts, rules, and applications in finding the rate of change and maxima/minima of functions. It explores techniques such as the product rule, quotient rule, and chain rule, along with derivatives of various function types, including trigonometric, exponential, and logarithmic functions. Additionally, it provides examples and exercises to illustrate the practical application of these differentiation principles.

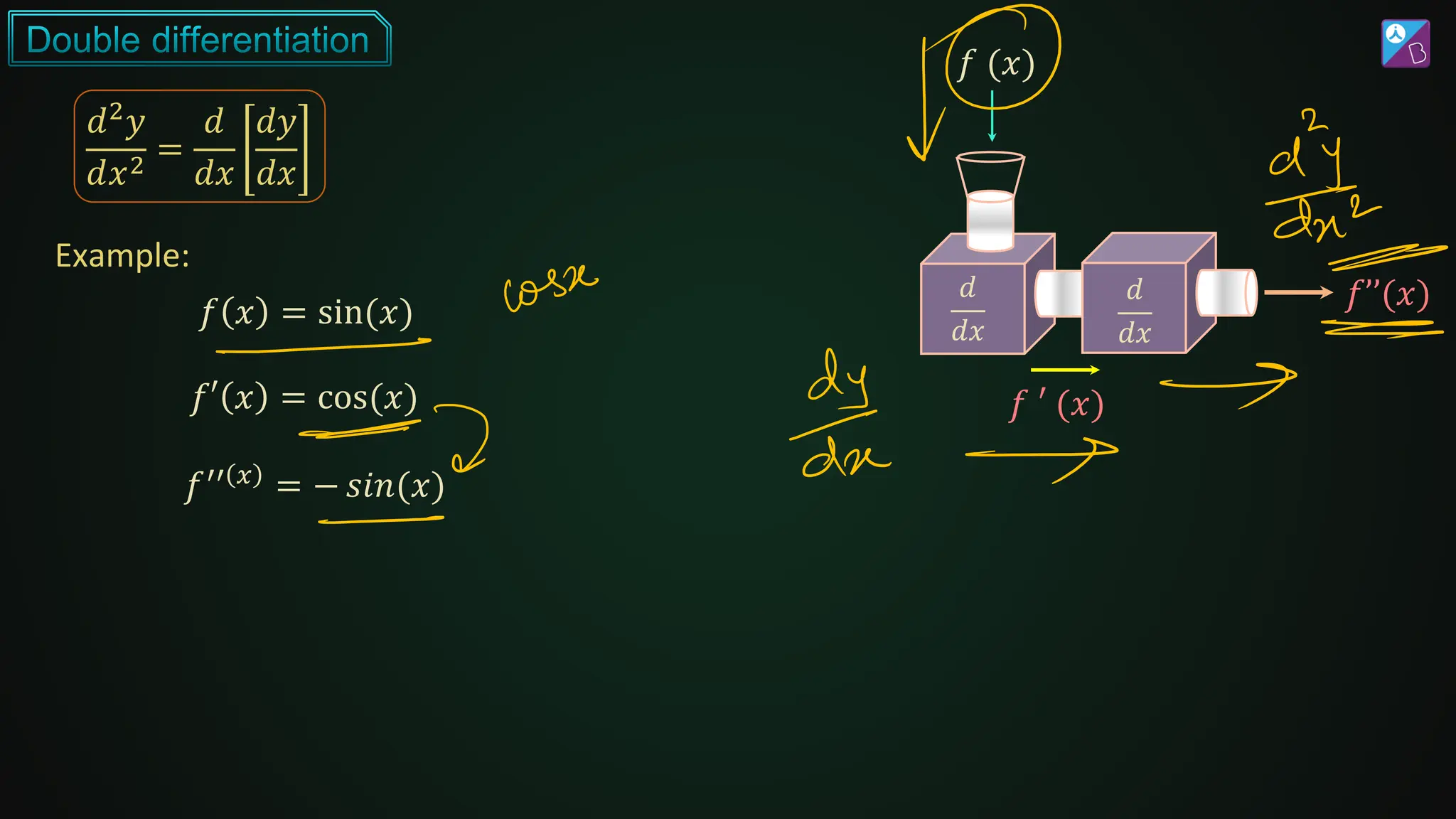
4. 𝑑2𝑦
𝑑𝑥2]
න
0
∞
𝑥𝑛
න
0
∞
𝑥𝑛
න
0
∞
𝑥𝑛
න
0
∞
𝑥𝑛
න
0
∞
𝑥𝑛
Differentiation
Properties of derivatives
Applications of derivatives

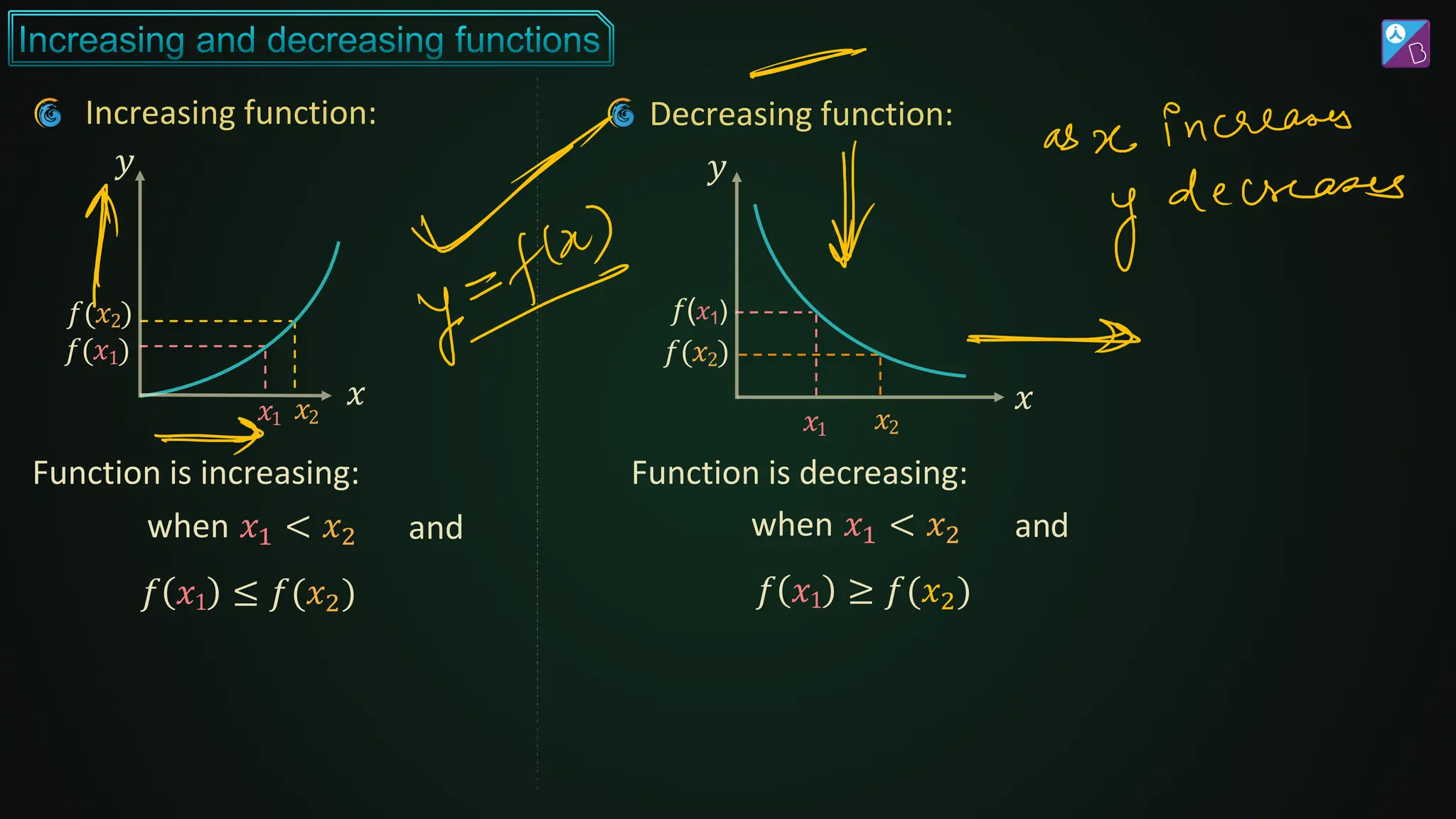
5. 𝑑2𝑦
𝑑𝑥2]
න
0
∞
𝑥𝑛
න
0
∞
𝑥𝑛
න
0
∞
𝑥𝑛
න
0
∞
𝑥𝑛
Differentiation
𝑑2𝑦
𝑑𝑥2]
න
0
∞
𝑥𝑛
න
0
∞
𝑥𝑛
න
0
∞
𝑥𝑛
න
0
∞
𝑥𝑛

6. To study the variation of one quantity with respect to another quantity.
To study slope of a curve.
To find the maximum and minimum values of any function.
Differentiation is all about finding rate of change of one quantity
with respect to another.

7. Speed =
distance
time
Acceleration =
change in velocity
time
Power =
work done
time
Counts per time ( eg. Heart rate,
radioactive decay rate ) Speed =
no.of counts
time
𝑣
𝑢
𝑡
𝑎

8. Tangent:
Secant:
Secant is a line which intersects a curve at two different points
𝑦
𝑥
𝐴
Δ𝑥
Δ𝑦
𝐵
𝑥
𝑦
𝐴
Δ𝑥
Δ𝑦
𝐵
𝑦
𝑥
𝐴
Δ𝑥
Δy
𝐵
𝑦
𝑥
Tangent
Secant
A line which touches a curve at one point
A limiting case of secant which intersects the
curve at two infinitesimally close points.

9. Tangent is the limiting case of secant:
Tangent
Secant
P
𝑥
𝑦
((𝑥, 𝑓(𝑥))
Δ𝑥
Q
R
S
(𝑥 + ∆𝑥, 𝑓(𝑥 + ∆𝑥))
Δ𝑦
For secant 𝑃𝑄,
Slope =
∆𝑦
∆𝑥
For tangent at 𝑃,
Slope = 𝑙𝑖𝑚
∆𝑥→0
∆𝑦
∆𝑥
=
𝑑𝑦
𝑑𝑥
= 𝑦′ = 𝑓′(𝑥)
ℎ
∆𝑥
∆𝑦
Slope
0
𝑑𝑥
𝑑𝑦
𝑑𝑦
𝑑𝑥
Derivative of a function at a point gives
slope of tangent at that point.

10. Derivative of a function:
Slope =
∆𝑦
∆𝑥
Slope = rate of change = 𝑙𝑖𝑚
∆𝑥→0
∆𝑦
∆𝑥
𝑓 (𝑥)
𝑑
𝑑𝑥 𝑓 ′ (𝑥)

11. 𝑑
𝑑𝑥
(𝑥𝑛
) = 𝑛𝑥𝑛−1
𝑑𝑦
𝑑𝑥
= 𝑦′ = 𝑓′(𝑥)
𝑓(𝑥) = 𝑥𝑛
Power rule of differentiation:

12. Differentiation of trigonometric functions:
(1)
𝑑
𝑑𝑥
sin 𝑥 = cos 𝑥
(2)
𝑑
𝑑𝑥
cos 𝑥 = − sin 𝑥
(3)
𝑑
𝑑𝑥
tan 𝑥 = sec2 𝑥
(4)
𝑑
𝑑𝑥
cot 𝑥 = − cosec2 𝑥
(5)
𝑑
𝑑𝑥
sec 𝑥 = sec 𝑥 tan 𝑥
(6)
𝑑
𝑑𝑥
cosec 𝑥 = − cosec 𝑥 cot 𝑥

13. Derivative of logarithmic function:
𝑑
𝑑𝑥
(𝑒𝑥) = 𝑒𝑥 𝑑
𝑑𝑥
(𝑎𝑥) = 𝑎𝑥 ln (𝑎)
𝑑
𝑑𝑥
(ln 𝑥) =
1
𝑥
"its slope is its value"
𝑦 = 𝑓(𝑥) = 𝑒𝑥
𝑥
𝑦
Derivative of exponential function:

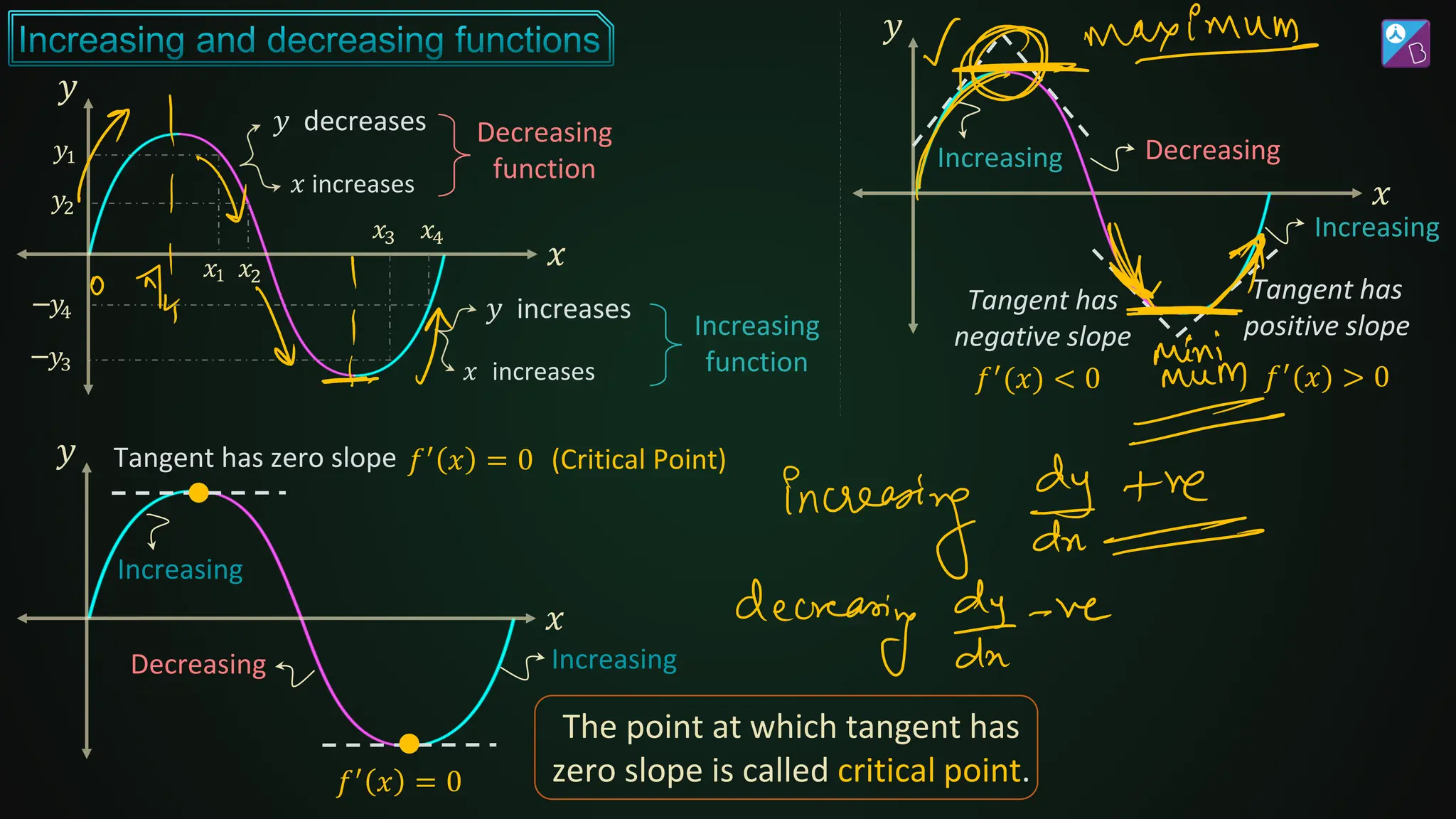
14. 𝑑2𝑦
𝑑𝑥2]
න
0
∞
𝑥𝑛
න
0
∞
𝑥𝑛
න
0
∞
𝑥𝑛
න
0
∞
𝑥𝑛
න
0
∞
𝑥𝑛
Differentiation
Properties of derivatives

15. Derivative of constant times a function:
𝑑
𝑑𝑥
𝑎𝑓 𝑥 = 𝑎
𝑑𝑓 𝑥
𝑑𝑥

16. 𝑑
𝑑𝑥
𝑓 𝑥 ± 𝑔(𝑥) =
𝑑𝑓 𝑥
𝑑𝑥
±
𝑑𝑔 𝑥
𝑑𝑥
Derivative of sum or difference of two functions:

17. Product rule:
𝑑 𝑓 𝑥 . 𝑔(𝑥)
𝑑𝑥
=
𝑑𝑓 𝑥
𝑑𝑥
𝑔 𝑥 +
𝑑𝑔 𝑥
𝑑𝑥
𝑓 𝑥

18. a) 𝑥 cos 𝑥 + 2𝑥 sin 𝑥
b) 𝑥2 cos 𝑥 + 𝑥2 sin 𝑥
c) 𝑥2
cos 𝑥 + 2𝑥 sin 𝑥
d) 𝑥2
cos 𝑥 − 2𝑥 sin 𝑥
For 𝑓(𝑥) = 𝑥2 cos 𝑥 ;
𝑑
𝑑𝑥
𝑓(𝑥) =?
Exercise

19. Applying,
𝑑
𝑑𝑥
𝑢 𝑣 = 𝑢
𝑑𝑣
𝑑𝑥
+ 𝑣
𝑑𝑢
𝑑𝑥
𝑑
𝑑𝑥
𝑓(𝑥) = −𝑥2 sin 𝑥 + 2𝑥 cos 𝑥
For 𝑓(𝑥) = 𝑥2 cos 𝑥 ;
𝑑
𝑑𝑥
𝑓(𝑥) =?
Solution

20. a) 𝑥 cos 𝑥 + 2𝑥 sin 𝑥
b) 𝑥2 cos 𝑥 + 𝑥2 sin 𝑥
c) −𝑥2
sin 𝑥 + 2𝑥 co𝑠 𝑥
d) 𝑥2
cos 𝑥 − 2𝑥 sin 𝑥
For 𝑓(𝑥) = 𝑥2 cos 𝑥 ;
𝑑
𝑑𝑥
𝑓(𝑥) =?
Answer

21. Division rule:
𝑑
𝑑𝑥
𝑓 𝑥
𝑔 𝑥
=
𝑑𝑓 𝑥
𝑑𝑥
𝑔 𝑥 −
𝑑𝑔 𝑥
𝑑𝑥
𝑓 𝑥
(𝑔 𝑥 )2

22. a)
cos 𝑥−𝑥 sin 𝑥
cos2𝑥
b)
cos 𝑥+𝑥 sin 𝑥
cos2𝑥
c)
cos 𝑥+𝑥 sin 𝑥
cos𝑥
d)
cos 𝑥+𝑥2 sin 𝑥
cos2𝑥
For 𝑓(𝑥) =
𝑥
cos 𝑥
;
𝑑
𝑑𝑥
𝑓(𝑥) =?
Exercise

23. 𝑑
𝑑𝑥
𝑢
𝑣
=
𝑣
𝑑𝑢
𝑑𝑥
− 𝑢
𝑑𝑣
𝑑𝑥
𝑣2
𝑑
𝑑𝑥
𝑓(𝑥) =
cos 𝑥 + 𝑥 sin 𝑥
cos2𝑥
𝑑
𝑑𝑥
𝑥
cos 𝑥
=
cos x
d
dx
x − x
d
dx
cos x
cos2x
For 𝑓(𝑥) =
𝑥
cos 𝑥
;
𝑑
𝑑𝑥
𝑓(𝑥) =?
Solution

24. a)
cos 𝑥−𝑥 sin 𝑥
cos2𝑥
b)
cos 𝑥+𝑥 sin 𝑥
cos2𝑥
c)
cos 𝑥+𝑥 sin 𝑥
cos𝑥
d)
cos 𝑥+𝑥2 sin 𝑥
cos2𝑥
For 𝑓(𝑥) =
𝑥
cos 𝑥
;
𝑑
𝑑𝑥
𝑓(𝑥) =?
Answer

25. Derivative of constant times a function:
𝑑
𝑑𝑥
𝑓 𝑥 ± 𝑔(𝑥) =
𝑑𝑓 𝑥
𝑑𝑥
±
𝑑𝑔 𝑥
𝑑𝑥
𝑑
𝑑𝑥
𝑎𝑓 𝑥 = 𝑎
𝑑𝑓 𝑥
𝑑𝑥
Derivative of sum or difference of two functions:
Product rule:
𝑑 𝑓 𝑥 . 𝑔(𝑥)
𝑑𝑥
=
𝑑𝑓 𝑥
𝑑𝑥
𝑔 𝑥 +
𝑑𝑔 𝑥
𝑑𝑥
𝑓 𝑥
Division rule:
𝑑
𝑑𝑥
𝑓 𝑥
𝑔 𝑥
=
𝑑𝑓 𝑥
𝑑𝑥
𝑔 𝑥 −
𝑑𝑔 𝑥
𝑑𝑥
𝑓 𝑥
(𝑔 𝑥 )2

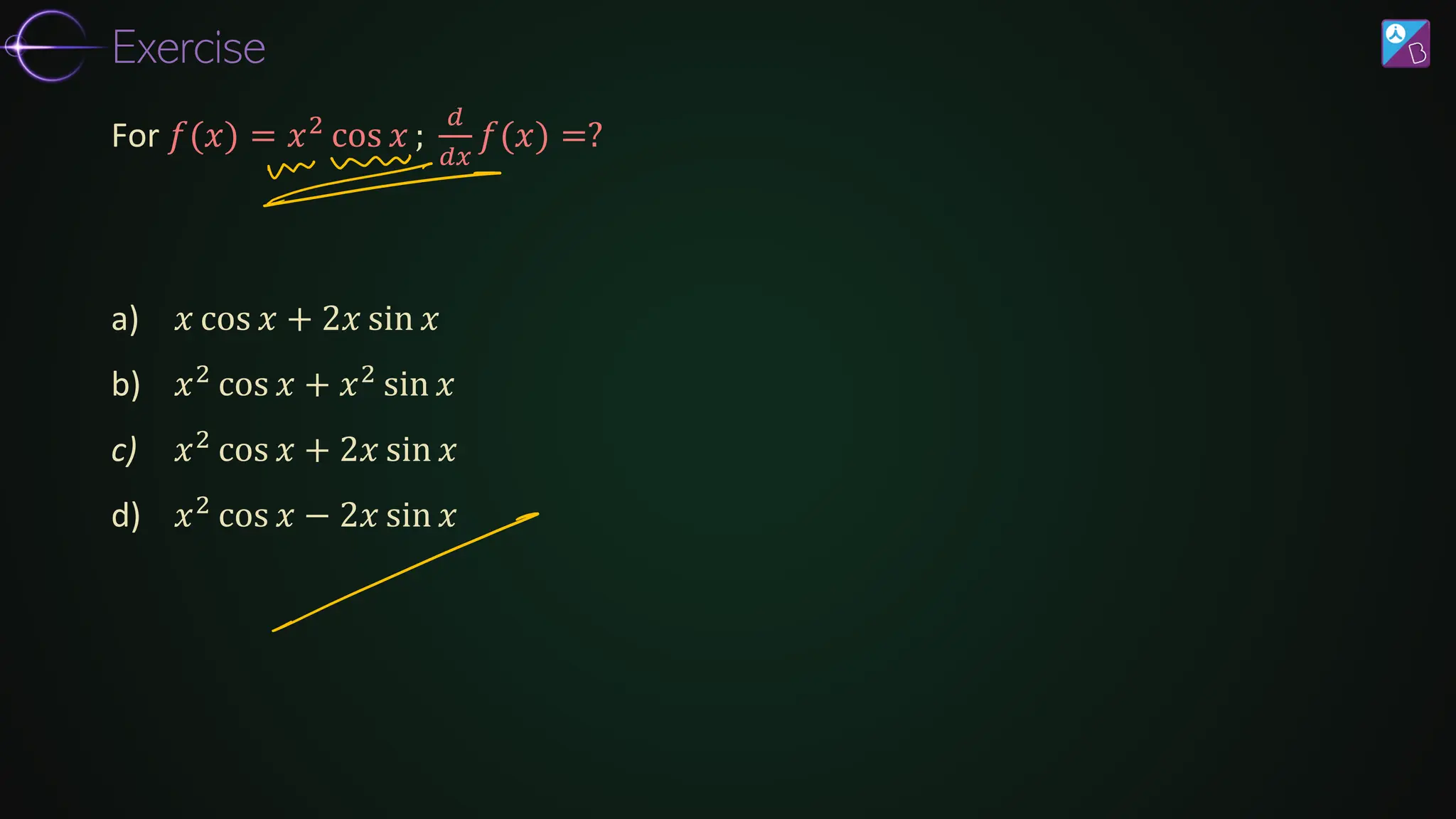
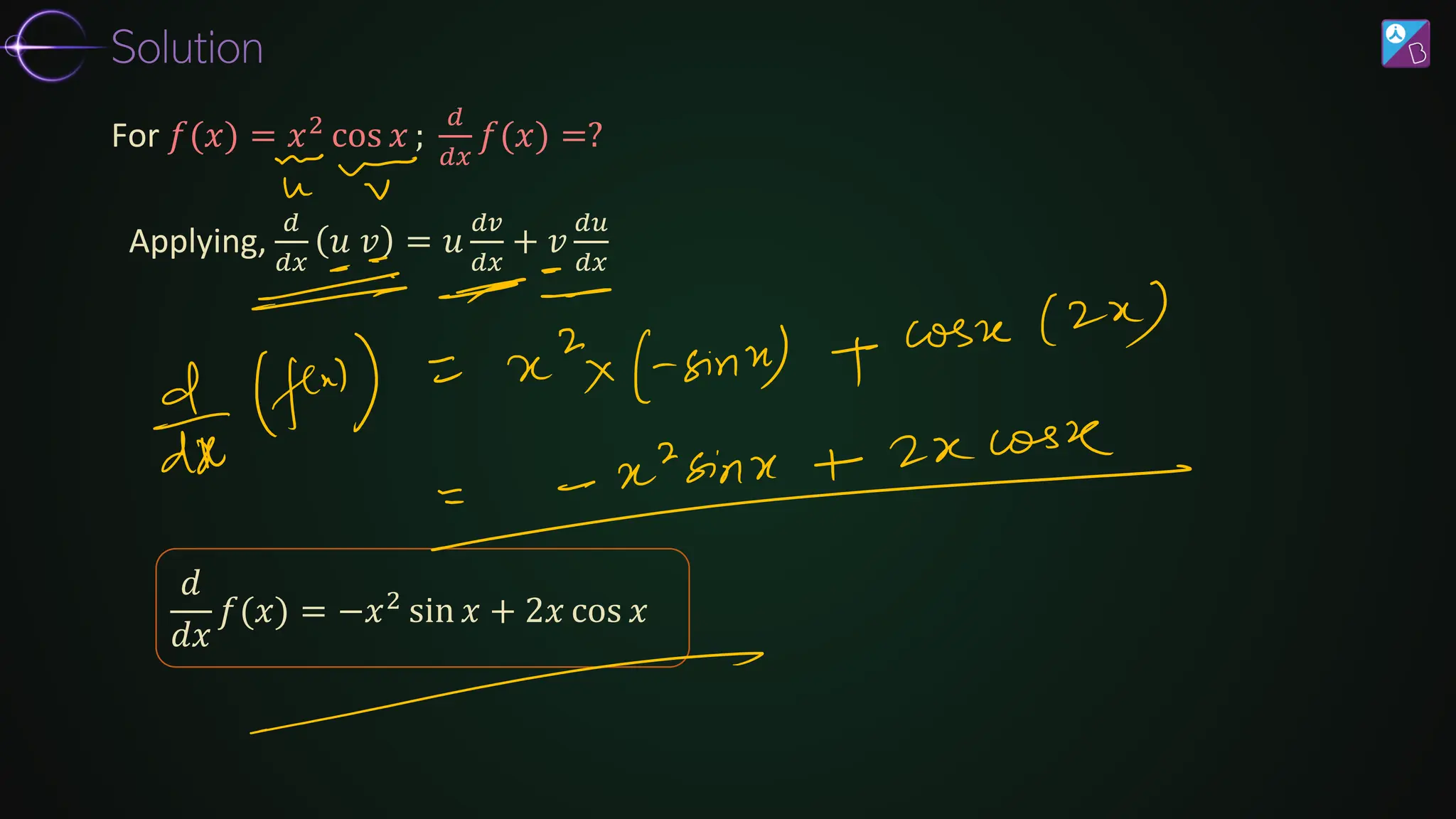
26. Chain rule:
𝑑𝑓
𝑑𝑥
=
𝑑𝑓
𝑑𝑔
.
𝑑𝑔
𝑑𝑥
Differentiate
outer function
Differentiate
inner function
If 𝑓 = 𝑓 (𝑔); 𝑔 = 𝑔 (𝑥)
𝑓’ (𝑥) = 𝑓’ ( 𝑔(𝑥) ) 𝑔’ (𝑥)
Example:
𝑓 𝑥 = sin(𝑥)
𝑔 𝑥 = 𝑥2
𝑓[𝑔 𝑥 ] = sin(𝑥2)

27. Exercise
a) 10𝑒10𝑥
b) 𝑒4𝑥
c)
𝑒4𝑥
4
d) 𝑒16𝑥
Differentiate 𝑓(𝑥) = 𝑒10𝑥

28. 𝑑
𝑑𝑥
𝑒10𝑥 = 10𝑒10𝑥
Differentiate 𝑓(𝑥) = 𝑒10𝑥
Solution

29. a) 10𝑒10𝑥
b) 𝑒4𝑥
c)
𝑒4𝑥
4
d) 𝑒16𝑥
Differentiate 𝑓(𝑥) = 𝑒10𝑥
Answer

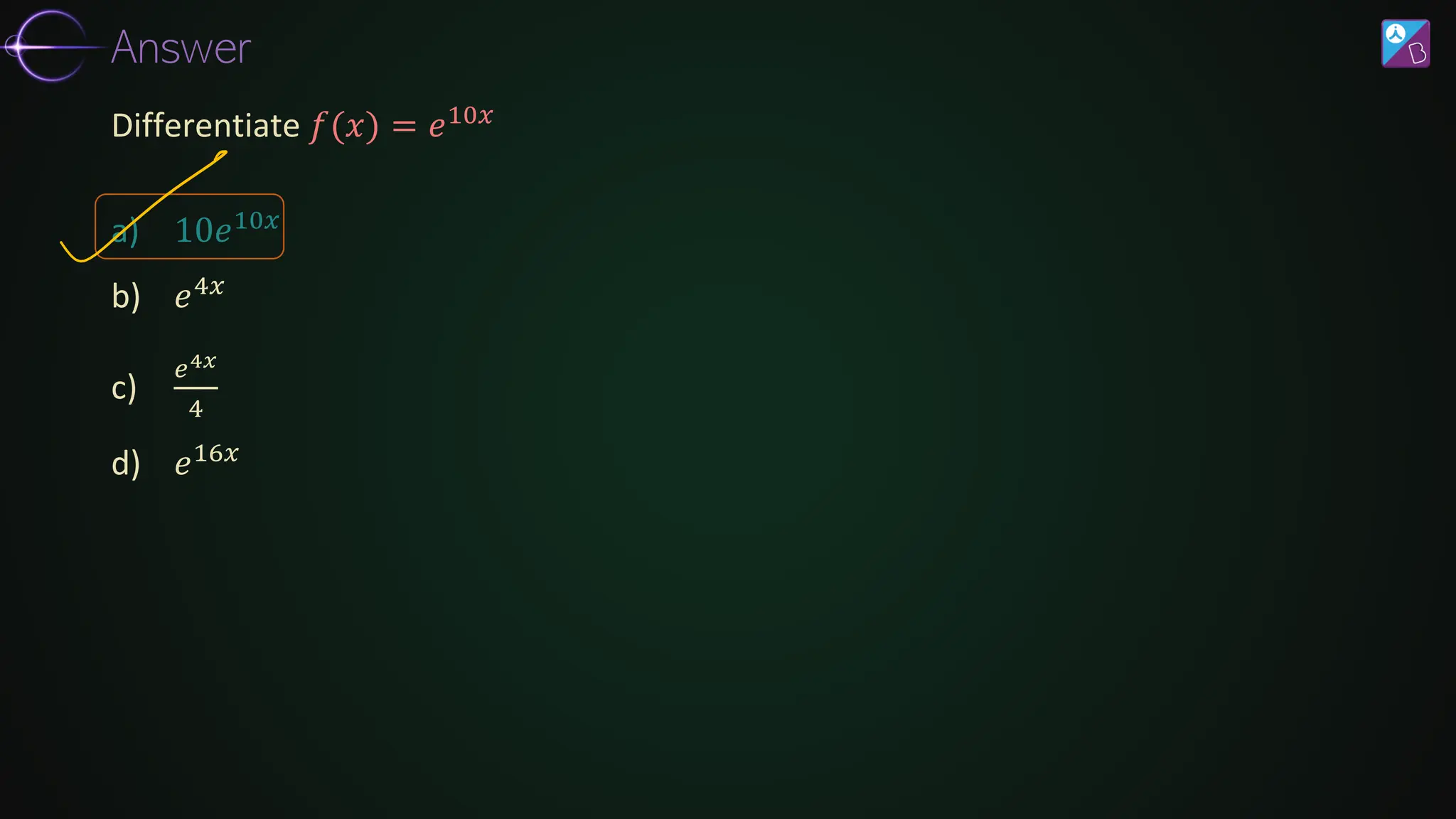
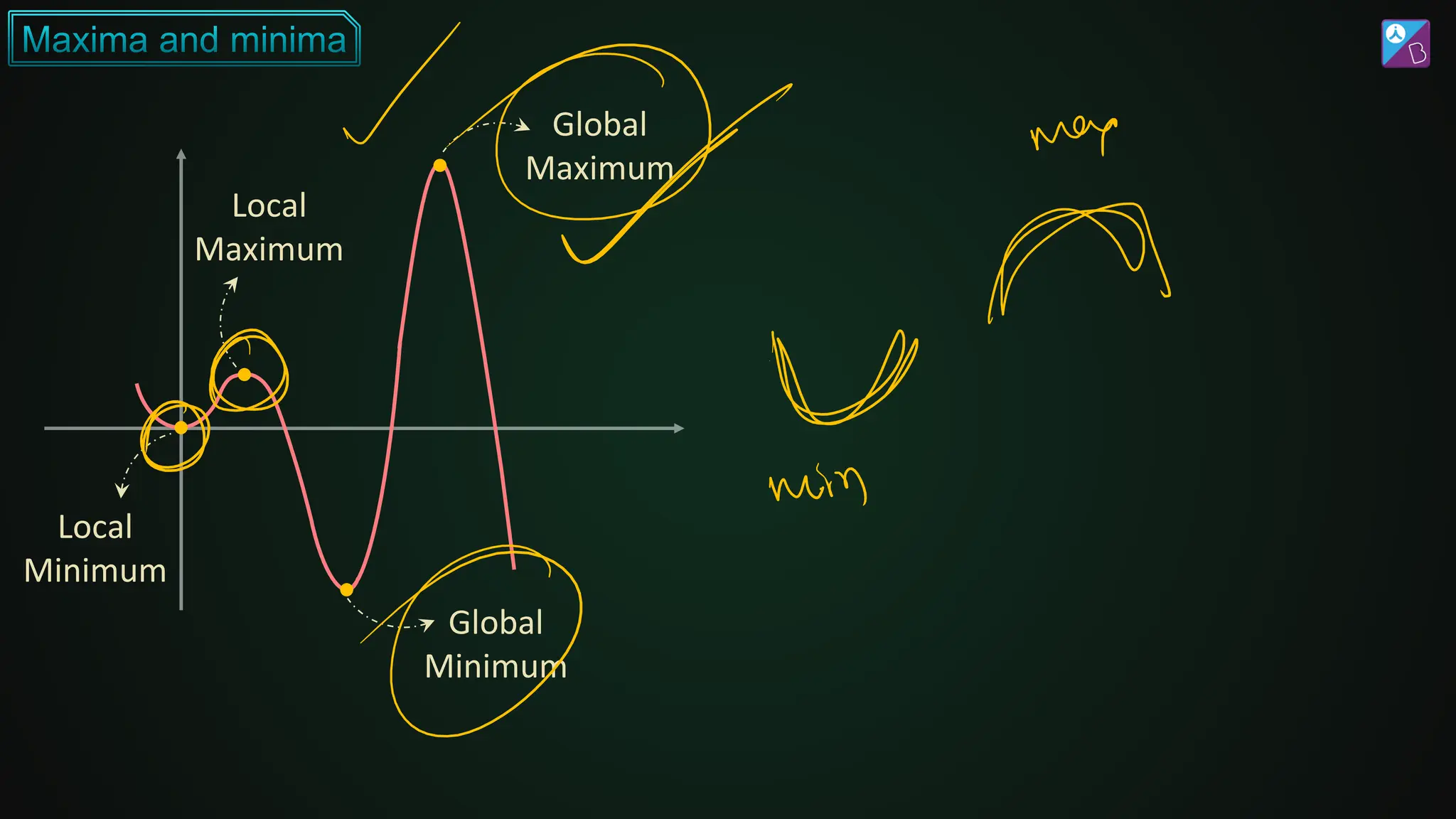
32. 𝑑2𝑦
𝑑𝑥2]
න
0
∞
𝑥𝑛
න
0
∞
𝑥𝑛
න
0
∞
𝑥𝑛
න
0
∞
𝑥𝑛
න
0
∞
𝑥𝑛
Differentiation
Properties of derivatives
Applications of derivatives

33. 𝑓 (𝑥)
f’(x)
𝑑
𝑑𝑥
𝑓’’(𝑥)
𝑑
𝑑𝑥
𝑓 ′ (𝑥)
𝑑2
𝑦
𝑑𝑥2
=
𝑑
𝑑𝑥
𝑑𝑦
𝑑𝑥
Example:
𝑓 𝑥 = sin(𝑥)
𝑓′ 𝑥 = cos(𝑥)
𝑓′′ 𝑥 = − 𝑠𝑖𝑛(𝑥)

34. Double-Differentiation of trigonometric functions:
(1)
(2)
𝑑2
𝑑𝑥2
sin 𝑥 = −sin 𝑥
𝑑2
𝑑𝑥2
cos 𝑥 = − cos 𝑥

35. 𝑓(𝑥1)
𝑓(𝑥2)
𝑥2
𝑥1
𝑥
𝑦
Increasing function: Decreasing function:
Function is increasing:
when 𝑥1 < 𝑥2
𝑓 𝑥1 ≤ 𝑓(𝑥2)
and
𝑓(𝑥2)
𝑓(𝑥1)
𝑥2
𝑥1
𝑥
𝑦
Function is decreasing:
when 𝑥1 < 𝑥2 and
𝑓 𝑥1 ≥ 𝑓(𝑥2)

36. 𝑥 increases
Decreasing
function
𝑦 decreases
𝑥 increases
𝑦 increases
Increasing
function
𝑥
𝑦
𝑥1 𝑥2
𝑥3 𝑥4
𝑦1
𝑦2
−𝑦3
−𝑦4
𝑥
𝑦
Tangent has
positive slope
Tangent has
negative slope
Increasing
Decreasing
Increasing
𝑓′(𝑥) > 0
𝑓′(𝑥) < 0
𝑥
𝑦 Tangent has zero slope
Decreasing Increasing
Increasing
𝑓′ 𝑥 = 0
𝑓′ 𝑥 = 0
(Critical Point)
The point at which tangent has
zero slope is called critical point.

38. Global
Maximum
Local
Maximum
Local
Minimum
Global
Minimum

39. 5
3
1
𝑦
𝑥
2 4
For maxima, as 𝑥 increases the slope decreases.
Condition for maxima:
𝑑𝑦
𝑑𝑥
= 0
𝑑2𝑦
𝑑𝑥2
< 0
and
5
1
𝑦
𝑥
2 3 4
For minima, as 𝑥 increases the
slope increases.
Condition for maxima:
𝑑𝑦
𝑑𝑥
= 0
𝑑2𝑦
𝑑𝑥2
> 0
and

40. To study the variation of one quantity with respect to another quantity.
Differentiation is all about finding rate of change of
one quantity with respect to another.
To study slope of a curve.
To find the maximum and minimum values of any function.
Instantaneous rate of change:
Rate of change of 𝑦 with respect to 𝑥 =
𝑐ℎ𝑎𝑛𝑔𝑒 𝑖𝑛 𝑦
𝑐ℎ𝑎𝑛𝑔𝑒 𝑖𝑛 𝑥
=
Δ𝑦
Δ𝑥
Velocity (𝑣) = rate of change of position(s) with respect to time
As 𝛥 → 0, Rate →
𝑑𝑦
𝑑𝑥
𝑣 =
𝑑𝑠
𝑑𝑡

41. a) 0.14 𝑚
b) 1.4 𝑚
c) 2.8 𝑚
d) 14 𝑚
A ball is thrown in the air. It’s height at any point is given by ℎ = 3 + 14𝑡 − 5𝑡2.
What is maximum height (𝑚) attained by the ball?
Exercise

42. For a maxima of a given function,
𝑓′
𝑥 = 0
14 − 10𝑡 = 0
A ball is thrown in the air. It’s height at any point is given by ℎ = 3 + 14𝑡 − 5𝑡2.
What is maximum height (𝑚) attained by the ball?
ℎ′ = 0 + 14 − 10𝑡
For maximum height, ℎ′= 0
𝑡 = 1.4 𝑚
Solution

43. a) 0.14 𝑚
b) 1.4 𝑚
c) 2.8 𝑚
d) 14 𝑚
A ball is thrown in the air. It’s height at any point is given by ℎ = 3 + 14𝑡 − 5𝑡2.
What is maximum height (𝑚) attained by the ball?
Answer

45. a) 3
b) −1
c) 1
d) −3
Find the local minima for the function, 𝑦 = 2𝑥3
− 6𝑥 + 2
Exercise

46. 𝑓′ 𝑥 = 0
𝑓"(1) = 12
Find the local minima for the function, 𝑦 = 2𝑥3
− 6𝑥 + 2
6𝑥2 − 6 = 0
𝑥 = ±1
𝑓"(𝑥) = 12𝑥
Given function has a local minima at 𝑥 = 1
Solution

47. a) 3
b) −1
c) 1
d) −3
Find the local minima for the function, 𝑦 = 2𝑥3
− 6𝑥 + 2
Answer