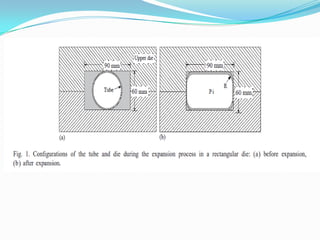
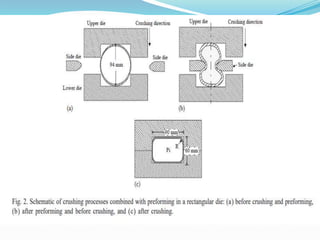
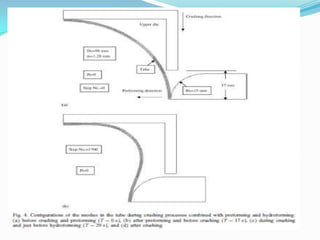
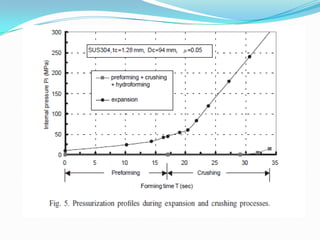
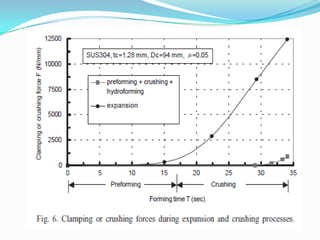
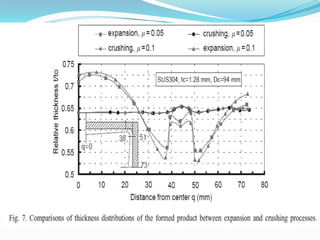
This document summarizes a student's presentation on using finite element modeling to simulate the plastic flow of circular tubes being hydraulically expanded or crushed into rectangular cross-sections. Key points include: using DEFORM software to model the tube expansion or crushing process under assumptions of plane strain and rigid tools; modeling the tube with 1000 elements over 6 thickness layers; and obtaining results on pressure requirements, thickness distributions, and conclusions that crushing requires less pressure and force than expansion while providing more uniform thickness.

1. Presented by
Khushboo Shrivastava
Roll No. 123370001

2. Aim
 Use the Finite Element Method to explore the plastic
flow pattern of a circular tube that is hydraulically
expanded or crushed into a rectangular cross-section.

3. DEFORM
 The plastic flow patterns of the forming tube and the
thickness distribution of the formed product are
explored while a circular tube is expanded or crushed
into a rectangular cross-section, using a commercially
available FE code “DEFORM”.

4. Finite element modeling
 An implicit and static FE code “DEFORM”
 The finite element code is based on the flow
formulation approach using an updated Lagrange
procedure. The basic equation for the finite element
formulation from the variational approach is

8. Finite Element Simulations
Assumptions
 Die is rigid, the tube is rigid-plastic,
 The plastic deformation of the tube is under a plane
strain state, and the interface between the tube
 Die has a constant friction coefficient
 The flow stress of the tube material of SUS 304 is
assumed to be expressed by a power law of its
equivalent strain, i.e.σ=Ke^n, where K = 1452 MPa is
the strength coefficient and n = 0.6 is the
strain-hardening exponent.

9. Modelling Parameter
 Four-node isoparametric elements are used.
 The tube is divided into about 1000 elements, and
there are six layers of elements in the thickness
direction.
 The configurations of the meshes in the tube before
crushing and preforming are shown in
Fig.

11. Iteration Methods
 Direct iteration methods
Generate a good initial guess for the Newton
Raphson method
 Newton-Raphson:
Speedy final convergence

13. Simulation works for expansion
 The upper die is always in contact with the bottom die
without movement.
 The internal pressure input into the tube is increased
gradually. Following the increase of the internal
pressure, the tube comes in contact with the short
sides of the die and then the corner radius of the free
bulged region, R, decreases. When the programmed
internal pressure reaches 300 MPa, the simulation is
stopped, and the corner radius and the thickness
distribution of the formed product are
measured.

14. Simulation works for crushing
 The dimension of the upper die is the same as that for
the expansion process. The step increment is set to be
0:01 s. At the beginning and early stage of the crushing
process, no internal pressure is input into the tube to
make the tube expanded outwards. On the contrary,
two side dies with a radius of 15 mm at the left and
right sides of the tube are used to push the tube
inwards to prevent the tube from being pinched by the
upper and lower dies as the upper die goes downwards.

15. Simulation works for crushing
 After the side dies move 17 mm inwards, as shown in
Fig. 4(b), the side dies move backwards immediately
and then the crushing process starts. As the upper die
is ready to touch the lower die, a gradually increased
pressure is input into the tube to calibrate the tube
and make the tube material 1ow into the corners of the
die as much as possible. The crushed and hydroformed
product is shown in Fig. 4(d).

17. Results from the simulation

22. Conclusions
From the simulation results, some conclusions can be
drawn as below:
 The maximum forming pressure needed by crushing
processes is only 5% of that by hydraulic expansion
processes.
 The maximum crushing force needed in the crushing
process is only about 7% of the clamping force in the
hydraulic expansion process.
 The thickness distribution of the formed product
obtained by crushing processes is much more uniform
than that by hydraulic expansion processes.

23. Conclusions
 The expansion process is a very simple forming process that
does not need extra equipment, such as the side dies and
cylinders, or a procedure control for the internal pressure
and movement of the dies. However, it needs a large press
machine and a high-pressure hydraulic system.
 By introducing the crushing process into the hydroforming
processes, the clamping forces and forming pressures
can be greatly reduced. Furthermore, highly uniform
thickness distributions of the formed products
can be obtained.

24. References
 F. Dohmann, Ch. Hartl, Tube hydroforming: research
and practical application, J. Mater. Proc. Technol. 71
(1997) 174–186
 Finite element analysis of tube hydroforming
processes in a rectangular die Yeong-Maw Hwanga; ∗,
Taylan Altanb

25. Thank you