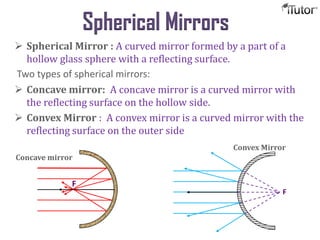
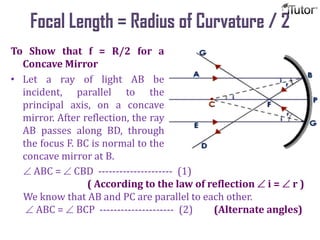
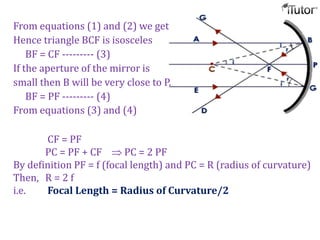
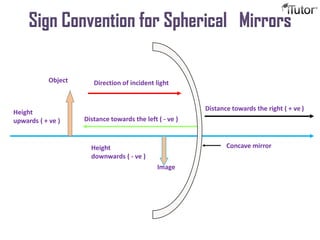
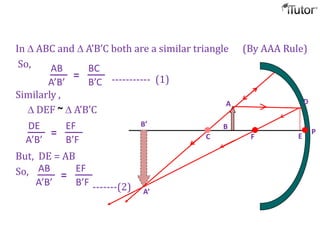
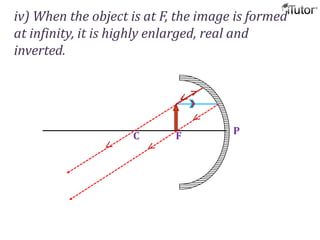
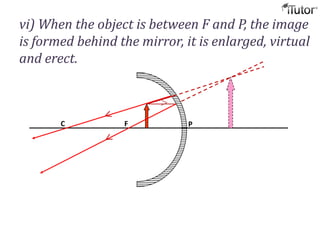
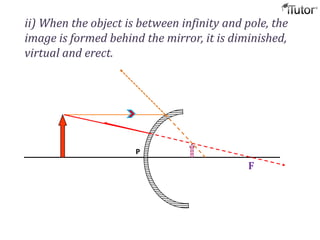
The document discusses different optical devices including lenses, mirrors, and prisms. It focuses on spherical mirrors, describing the two types - concave and convex mirrors. Key details are provided on the center of curvature, radius of curvature, principal axis, pole, focus, and focal length. The mirror formula relating object distance, image distance, and focal length is defined. Characteristics of images formed by concave and convex mirrors in different situations are explained. Uses of concave and convex mirrors are also noted.

1. Spherical
Mirrors
T- 1-855-694-8886
Email- info@iTutor.com
By iTutor.com

2. Optical Device
 A lens is an optical device that is used to bend light in a
specific way.
 A converging lens bends light so that the light rays come
together to a point.
 A diverging lens bends light so it spreads light apart instead
of coming together.
 Mirrors reflect light and allow us to see ourselves.
 A prism is another optical device that can cause light to
change directions.
 A prism is a solid piece of glass with flat polished surfaces.

3. Spherical Mirrors
 Spherical Mirror : A curved mirror formed by a part of a
hollow glass sphere with a reflecting surface.
Two types of spherical mirrors:
 Concave mirror: A concave mirror is a curved mirror with
the reflecting surface on the hollow side.
 Convex Mirror : A convex mirror is a curved mirror with the
reflecting surface on the outer side
Convex Mirror
Concave mirror
F
F

4.  Centre of Curvature : The centre of curvature of a curved
mirror is defined as the center of the hollow glass sphere
of which the curved mirror was (previously) a part.
 Radius of curvature: The radius of the hollow glass sphere
of which the spherical mirror was a part.
 Principal Axis : The imaginary line passing through its pole
P and center of curvature C.
 Pole : The pole is defined as the geometric center of the
curved mirror.
 Focus :The principal focus is defined as the point on
The principal axis where the light rays traveling parallel
to the principal axis after reflection actually meet.

5.  The focal length is the distance between the pole P and the
Principal focus F of a curved mirror.
 The focal length is half the radius of curvature.
Focal Length = Radius of Curvature/2
Focal length

6. Focal Length = Radius of Curvature / 2
To Show that f = R/2 for a
Concave Mirror
• Let a ray of light AB be
incident, parallel to the
principal axis, on a concave
mirror. After reflection, the ray
AB passes along BD, through
the focus F. BC is normal to the
concave mirror at B.
ABC = CBD --------------------- (1)
( According to the law of reflection i = r )
We know that AB and PC are parallel to each other.
ABC = BCP --------------------- (2) (Alternate angles)

7. From equations (1) and (2) we get
Hence triangle BCF is isosceles
BF = CF --------- (3)
If the aperture of the mirror is
small then B will be very close to P.
BF = PF --------- (4)
From equations (3) and (4)
CF = PF
PC = PF + CF PC = 2 PF
By definition PF = f (focal length) and PC = R (radius of curvature)
Then, R = 2 f
i.e. Focal Length = Radius of Curvature/2

8. i) The object is always placed on the left of the mirror and light
from the object falls from the left to the right.
ii) All distances parallel to the principal axis are measured from
the pole.
iii) All distances measured to the right of the pole are taken as +
ve.
iv) All distances measured to the left of the pole are taken as – ve.
v) The height measured upwards perpendicular to the principal
axis is taken as + ve.
vi) The height measured downwards perpendicular to the principal
axis is taken as – ve.
Sign Convention for Spherical Mirrors

9. Direction of incident light
Distance towards the left ( - ve )
Distance towards the right ( + ve )
Height
downwards ( - ve )
Height
upwards ( + ve )
Concave mirror
Object
Image
Sign Convention for Spherical Mirrors

10. Mirror Formula
Mirror formula is the relationship between object distance
(u), image distance (v) and focal length
Mirror formula of the Concave Mirror is
A
B
A’
B’
C F
P
D
1
f
=
1
v
+
1
u
Here an object AB at a
distance u from the
pole. The image A’B’ is
formed at a distance v
from the mirror. The
position of the image is
obtained by drawing a
ray diagram.
E

11. In ABC and A’B’C both are a similar triangle (By AAA Rule)
So,
----------- (1)
Similarly ,
DEF ~ A’B’C
But, DE = AB
So,
-------(2)
A
B
A’
B’
C F
P
D
AB
A’B’
BC
B’C
=
E
DE
A’B’
EF
B’F
=
AB
A’B’
EF
B’F
=

12. Mirror FormulaFrom (1) and (2)
If D is very close to P then EF = PF
By sign convention
PC = -R, PB = -u,
PF = -f and PB’ = -v
A
B
A’
B’
C F
P
D
BC
B’C
E
EF
B’F
=
BC
B’C
PF
B’F
=
We Know , BC = PC – PB and B’C = PB’ –PC
B’F = PB’- PF
PC - PB
PB’ - PC
PF
PB’ - PF
=

13. vR – uv – fR + uf = vf – fR
vR – vf – uv = - uf
vf – uv = -uf
Divided by uvf both side
Or
A
B
A’
F
P
D
E
(-R) – (-u)
(-v) – (-R)
(-f)
(-v) – (-f)
=
B’
-R + u
-v + R
-f
-v + f
=or
1
u
–
1
f
=
1
v
–
1
f
=
1
v
+
1
u

14. i) When the object is at infinity the image is formed at
the focus, it is highly diminished, real and inverted.
Images formed by concave mirror
PFC

15. ii) When the object is beyond C, the image is
formed between C and F, it is diminished, real
and inverted.
C F P

16. iii) When the object is between C and F, the image
is formed beyond C, it is enlarged, real and
inverted.
C
F
P

17. iv) When the object is at F, the image is formed
at infinity, it is highly enlarged, real and
inverted.
FC P

18. vi) When the object is between F and P, the image
is formed behind the mirror, it is enlarged, virtual
and erect.
C F P

19. Uses of Concave Mirrors
 Concave mirrors are used in torches, search lights and head lights
of vehicles to get parallel beams of light.
 They are used as shaving mirrors to see larger image of the face.
 They are used by dentists to see larger images of the teeth.
 Large concave mirrors are used to concentrate sunlight to produce
heat in solar furnaces.

20. Images formed by Convex Mirror
i) When the object is at infinity, the image is formed at F
behind the mirror, it is highly diminished, virtual and
erect.
F
P

21. F
P
ii) When the object is between infinity and pole, the
image is formed behind the mirror, it is diminished,
virtual and erect.

22. Uses of Convex Mirrors
Convex mirrors are used as rear-view mirrors in vehicles.
Convex mirrors give erect diminished images of objects. They
also have a wider field of view than plane mirrors.

23. Magnification for spherical mirrors is the ratio of the height of
the image to the height of the object.
The magnification is also related to the object distance and
image distance. It is expressed as :-
Magnification for spherical mirrors
Magnification of Mirror
the ObjectHeight of
agetheHeight of
ionMagnificat
Im
o
i
h
h
m
u
v
h
h
mionMagnificat o
i

24. Call us for more
Information:
www.iTutor.com
1-855-694-8886
Visit
The End