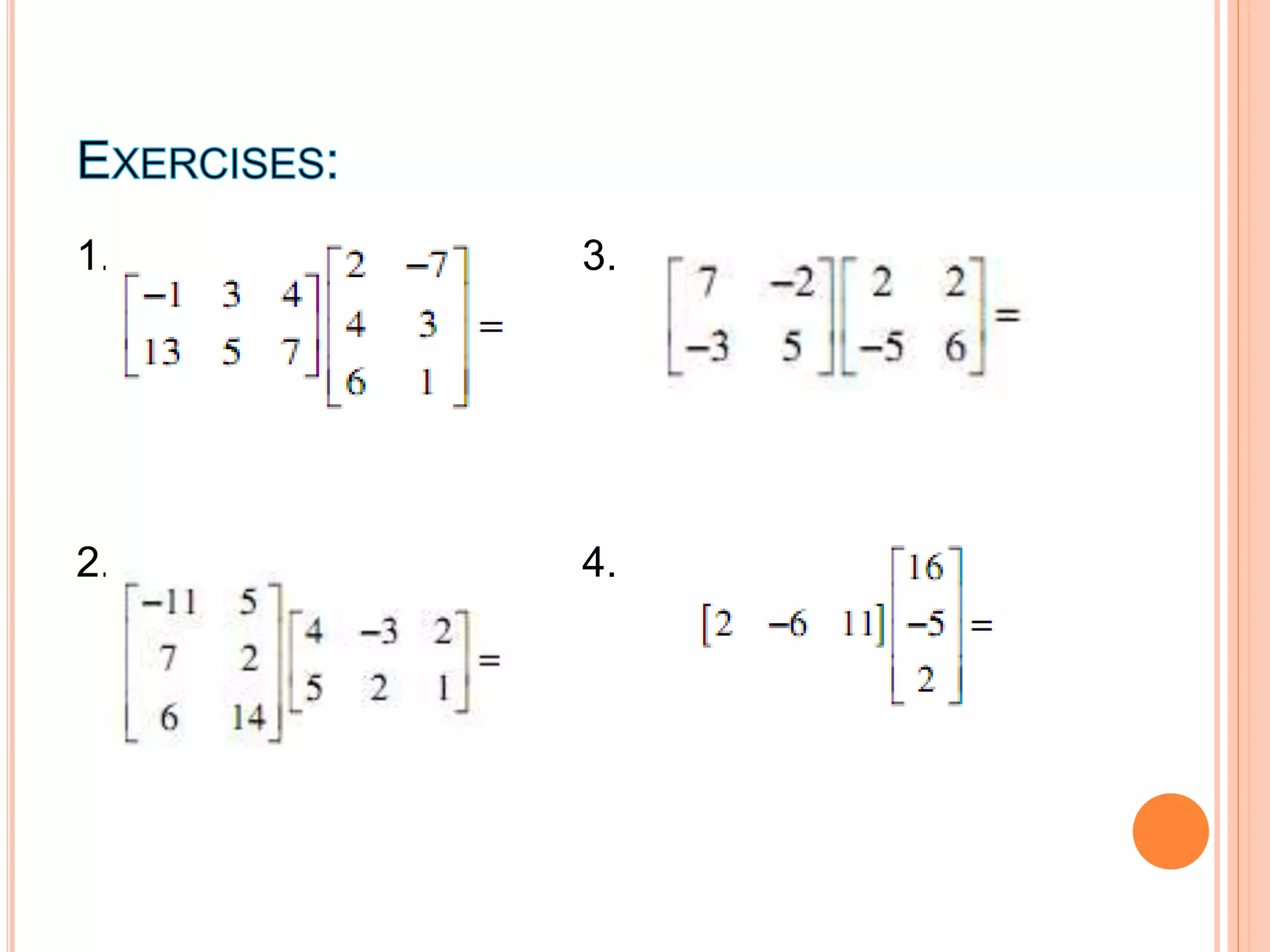The document discusses matrix multiplication. Matrix multiplication involves multiplying the elements of each row of the first matrix by the elements of each column of the second matrix and adding the products. The number of columns in the first matrix must equal the number of rows in the second matrix for the multiplication to be defined. The result of multiplying an m×n matrix by an n×p matrix is an m×p matrix. Matrix multiplication is not generally commutative.

2. 4 6 9 1 6
3 8 7 2 3
0 1 2 7 9
3x3 3x2
It is the multiplication of an
entire matrix by another entire
matrix.
E.g.

4.  (1, 2, 3) • (8, 10, 12) = 1×8 + 2×10 + 3×12 = 64
 (4, 5, 6) • (7, 9, 11) = 4×7 + 5×9 + 6×11 = 139
 And for the 2nd row and 2nd column:
 (4, 5, 6) • (8, 10, 12) = 4×8 + 5×10 + 6×12 = 154

5. In General:
To multiply an m×n matrix by
an n×p matrix, the ns must be the
same,
and the result is an m×p matrix.

6.  The number of columns of the 1st
matrix must equal the number of rows
of the 2nd matrix.
 And the result will have the same
number of rows as the 1st matrix, and
the same number of columns as the 2nd
matrix.

7.  In arithmetic we are used to:
 3 × 5 = 5 × 3
(The Commutative Law of
Multiplication)
 But this is not generally true for
matrices (matrix multiplication is not
commutative):

8. Example:
See how changing the order affects
this multiplication.
AB ≠ BA
When you change the order of
multiplication, the answer is
(usually) different.

9.  You can multiply two matrices if, and only if, the
number of columns in the first matrix equals the
number of rows in the second matrix.
 Otherwise, the product of two matrices is
undefined.

10.  Step 1: Make sure that the number of columns in
the 1st one equals the number of rows in the
2nd one. (The pre-requisite to be able to multiply)
 Step 2: Multiply the elements of each row of the
first matrix by the elements of each column in the
second matrix.
 Step 3: Add the products.

11. 1. (6*-4)+(-2*8)+(5*3)
(1*-4)+(6*8)+(2*3)
(-3*-4)+(4*8)+(7*3)
-24 + -16 + 15
-4 + 48 + 6
12 21+32+
=
=

12. 2.
=
(4*-3)+(2*2)+(0*-1) (4*5)+(2*3)+(0*8) (4*6)+(2*-2)+(0*9) (4*7)+(2*4)+(0*0)
=
(-4*-3)+(-2*2)+(-1*-1) (-4*5)+(-2*3)+(-1*8) (-4*6)+(-2*-2)+(-1*9) (-4*7)+(-2*4)+(-1*0)
-12+4+0 20+6+0 24+-4+0 28+8+0
12+-4+1 -20+-6+-8 -24+4+-9 -28+-8+0
=
-8
9
2026
-34 -36-29
36

13. 1.
2.
3.
4.

14. 5. Multiply

15.  http://www.mathopolis.com/questions/q.php?id=658
8