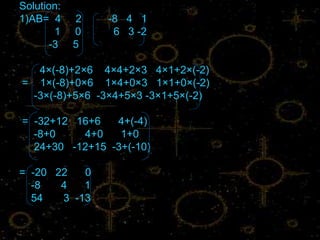
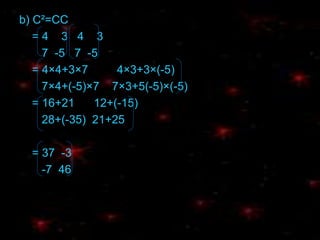
The document discusses matrix multiplication. It states that two matrices can be multiplied if and only if the number of columns in the left matrix is equal to the number of rows in the right matrix. It provides examples of determining if matrix multiplication is possible and examples of calculating products of matrices. It also discusses solving matrix equations involving matrix multiplication.

2. Determining whether the two matrices can be multiplied
The multiplication of two matrices is possible if and only if the number of columns in
the left matrix is the same as the number of rows in the right matrix.
If two matrices can be multiplied, then the number of rows of the product (matrix R) will
be the same as the number of rows of the left matrix (matrix P). The number of columns
of the product (matrix R) will be the same as the number of columns on the right matrix
(matrix Q). See below.

3. Example 1 :Determine whether the matrix
multiplication is possible for each of the matrix
equations shown below.State the order of the matrix
formed if the multiplication is possible
a) 5 3
1 9 4 3
Solution
a)Order of matrix:2 × 2 and 1 × 2
Not the same
Thus,Matrix multiplication is not possible

4. b)
4 7
3 8 4 5
9 6 6 7
Order of matrix :3 × 2 and 2 × 2
Same
Thus,matrix multiplication is possible
The order of matrix formed is 3 × 2

5. Finding the product of two
matrices
 If two matrices of order m x n and n x p is multiplied
then the matrix formed is of the order m x p.
 The multiplication process involves multiplying the
elements of the 1st row of the first matrix with the
elements of each column on the second matrix.
 Repeat the process for all other rows in the first matrix.

6. Example 2
Find the product of each of the following
a) 3
4 1 2
Solution
3
4 1 2 = 3x1 3x2
4x1 4x2
= 3 6
4 8

7.  Solving matrix equations involving the multiplication of two
matrices
 To find the unknowns element in a matrix can be achieved by solving
matrix equation involving the multiplication of two matrices as
follows:
 I. Simplify the matrix equations so that the multiplication form two
equal matrices.
II. Compare their corresponding elements in the two equal matrices
formed. The comparison allows to write down linear equation where
the values of unknown elements can be determined.

8. Example 3
If 2 4 6 ,find the value of x+y
x ( y 3)= 8 9
Solution:
2 4 6
x y 3 = 8 9
2y 6 = 4 6
xy 3x 8 9
Compare the corresponding elements:
Hence,2y=4 3x=9
y=2 x=3
Thus, xy =2(3)
=6

9. Exercise
1)Give A= 4 2 ,B= -8 4 1 and C= 4 3
1 0 6 3 -2 7 -5
-3 5
a)Find AB and BA.Is AB=BA?
b)Find C².
2)Find the unknows
a) a 3 1 2 = -13 4
2 b -3 4 5 0
b) 4 y 2 2 = 5 17
x -1 -1 3 5 1

10. Solution:
1)AB= 4 2 -8 4 1
1 0 6 3 -2
-3 5
4×(-8)+2×6 4×4+2×3 4×1+2×(-2)
= 1×(-8)+0×6 1×4+0×3 1×1+0×(-2)
-3×(-8)+5×6 -3×4+5×3 -3×1+5×(-2)
= -32+12 16+6 4+(-4)
-8+0 4+0 1+0
24+30 -12+15 -3+(-10)
= -20 22 0
-8 4 1
54 3 -13

11. BA= -8 4 1 4 2
6 3 -2 1 0
-3 5
= (-8)×4+4×1+1×(-3) (-8)×2+4×0+1×5
6×4+3×1+(-2)×(-3) 6×2+3×0+(-2)×5
= -32+4+(-3) -16+0+5
24+3+6 12+0+(-10)
= -31 -11
33 2 Therefore,AB≠BA

12. b) C²=CC
=4 3 4 3
7 -5 7 -5
= 4×4+3×7 4×3+3×(-5)
7×4+(-5)×7 7×3+5(-5)×(-5)
= 16+21 12+(-15)
28+(-35) 21+25
= 37 -3
-7 46

13. 2a) a 3 1 2 = -13 4
2 b -3 4 5 0
a(1)+3(-3) a(2)+3(4) = -13 4
2(1)+b(-3) 2(2)+b(4) 5 0
a-9 2a+12 = -13 4
2-3b 4+4b 5 0
Hence:
a-9=-13 2-3b=5
a=-13+9 -3b=5-2
a=-4 -3b=3
b=-1

14. 2b) 4 y 2 2 = 5 17
x -1 -1 3 5 1
4(2)+y(-1) 4(2)+y(3) 5 17
x(2)+-1(-1) x(2)-1(3) = 5 1
8-y 8+3y = 5 17
2x+1 2x-3 5 1
Hence:
8-y=5 2x+1=5
-y=-3 2x=4
y=3 x=2

15. 3) Given
D= 4 3 ,E= 1 0
2 -1 0 1
Find the product of DE

16. SOLUTION
= 1×4+0×2 1×3+0×(-1)
0×4+1×2 0×3+1×(-1)
= 4 3
2 -1

17. 4)
A= 4 2 2 ,B= 8
2 4 2 10
6 2 0 12
Find the product of AB

18. SOLUTION
= 4×8+ 2×10+ 2×12
2×8+ 4×10+ 2×12
6×8+ 2×10+ 0×12
= 16+10+12 = 38
8+20+12 40
24+10+0 34