Downloaded 149 times
Uploaded byGaditek
Relations
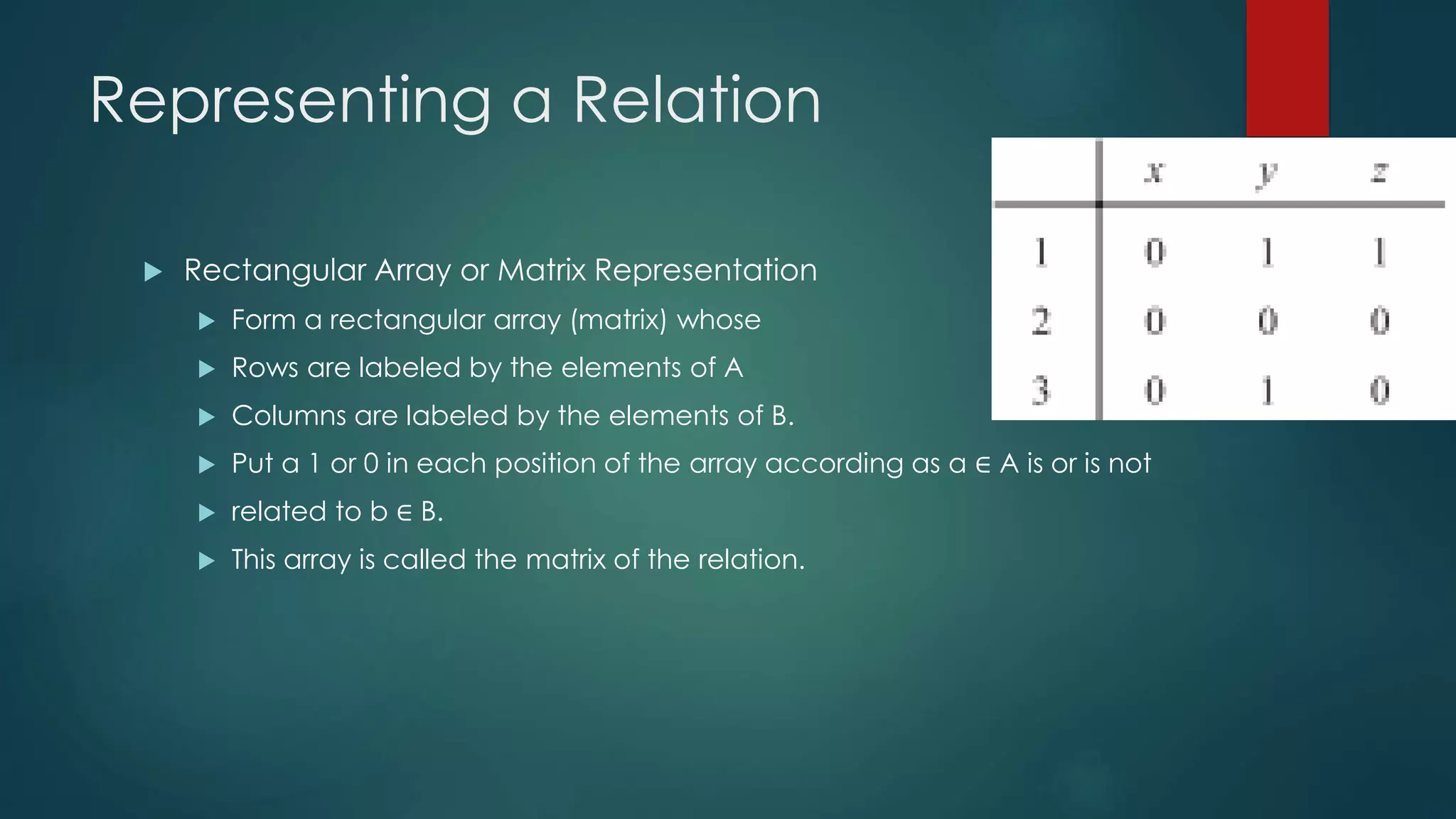
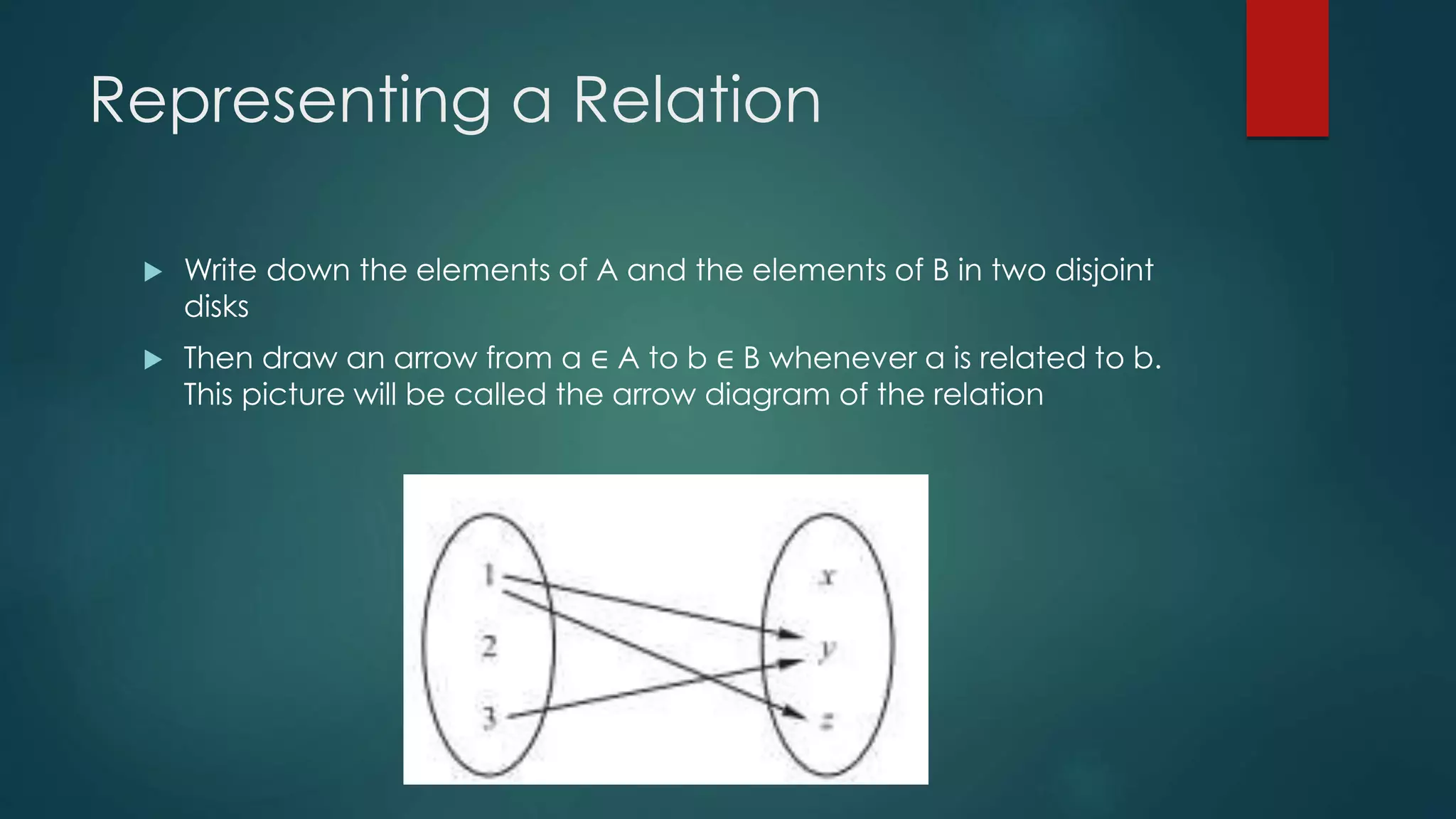
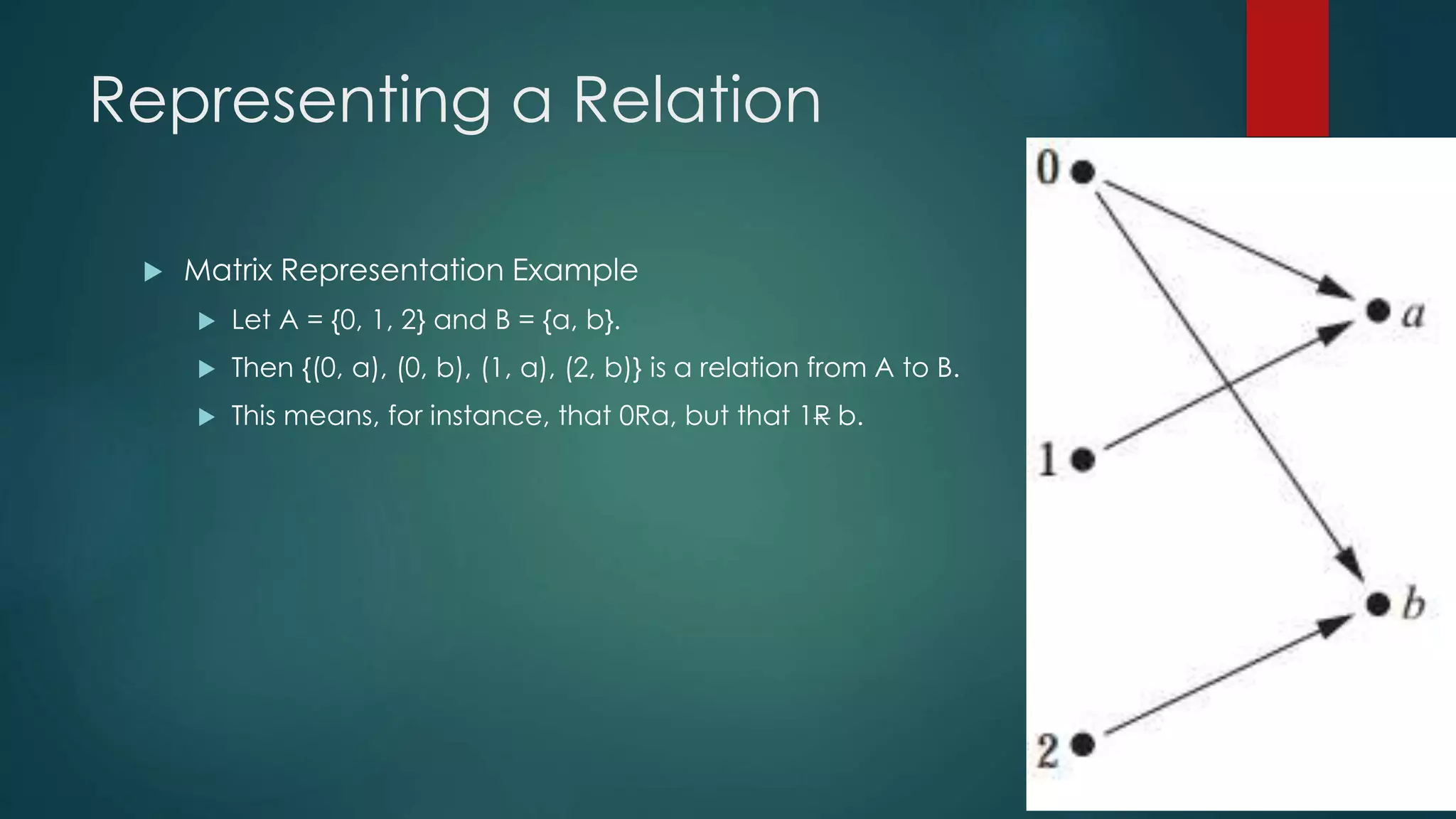
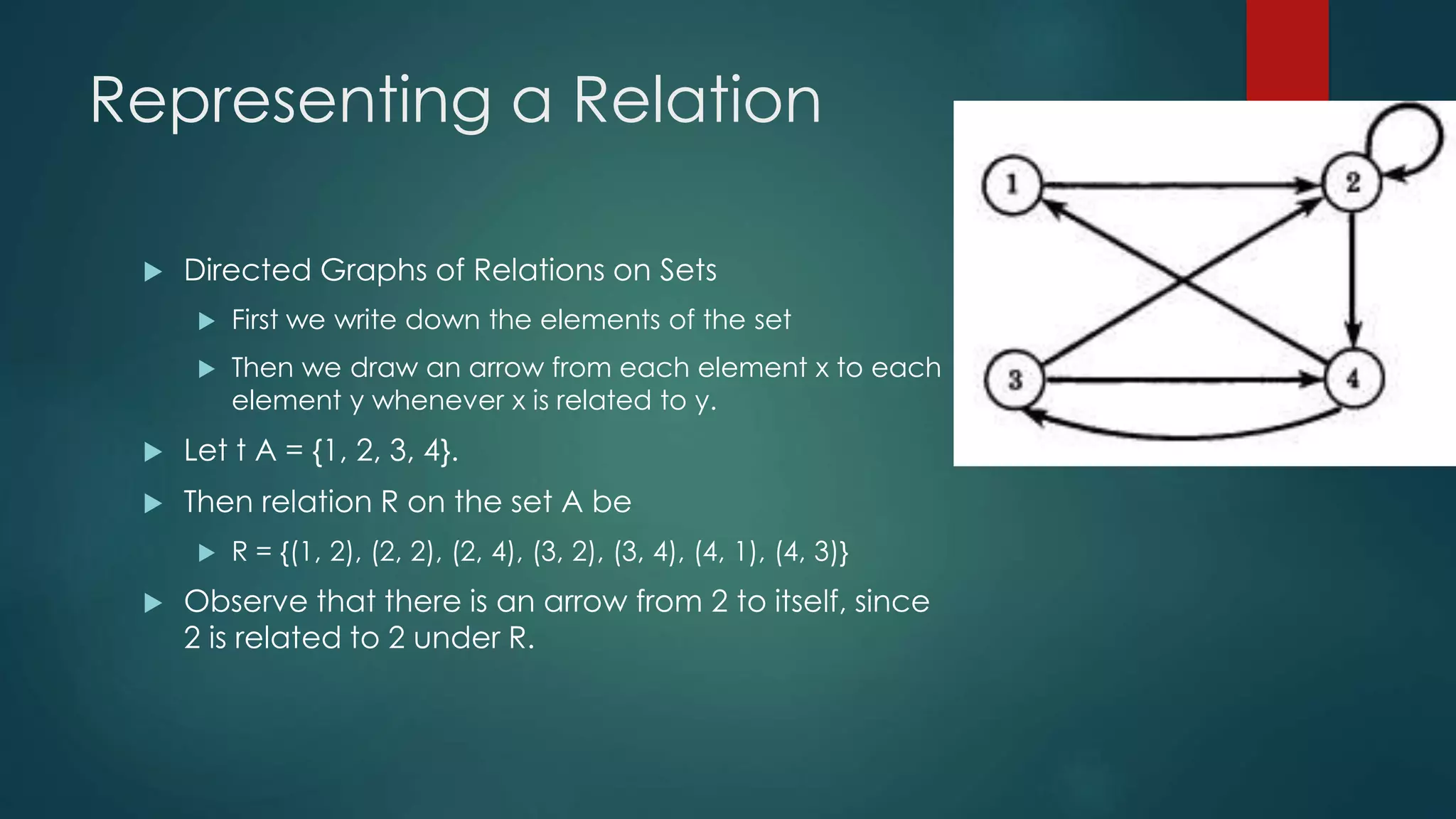
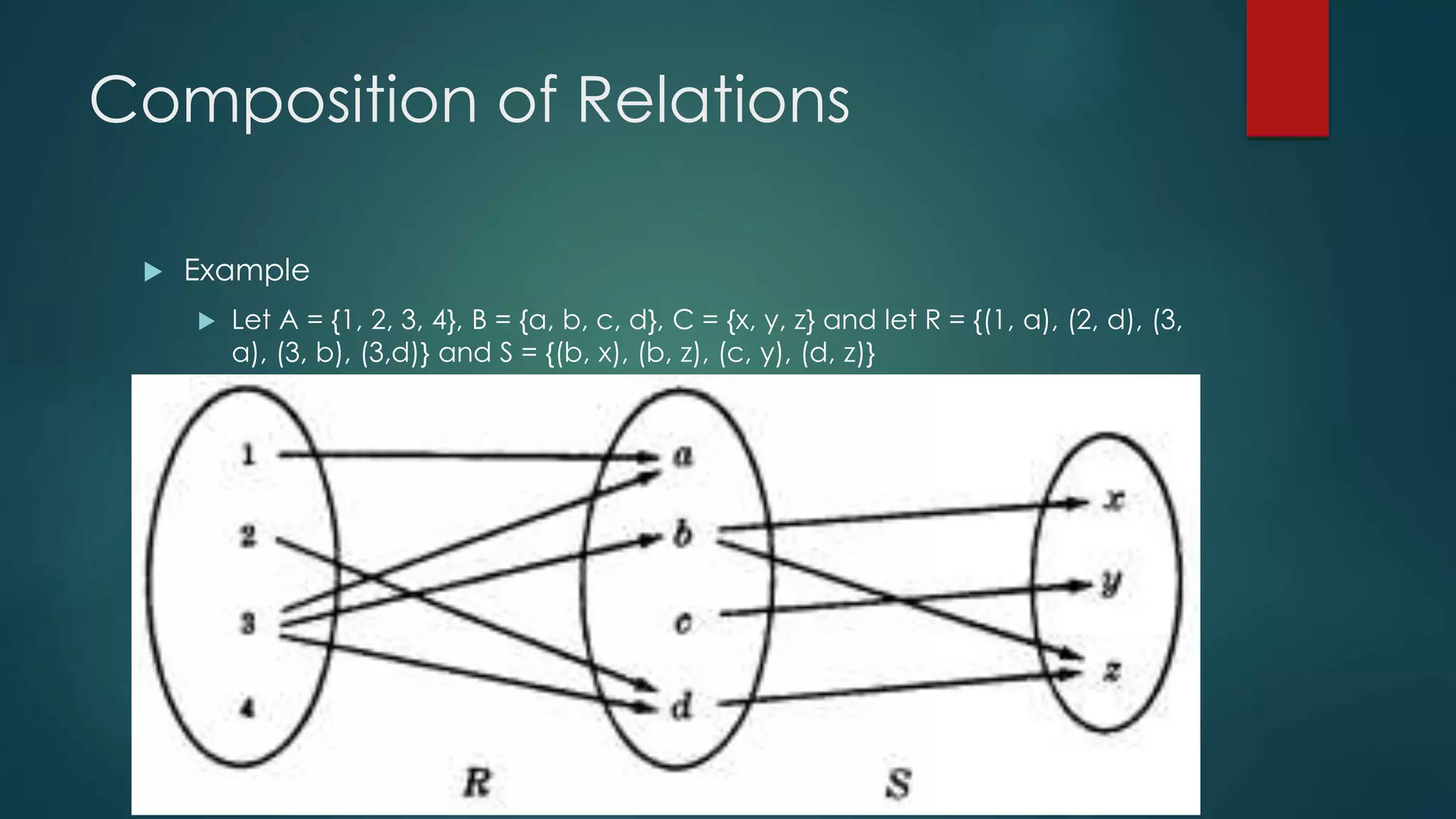
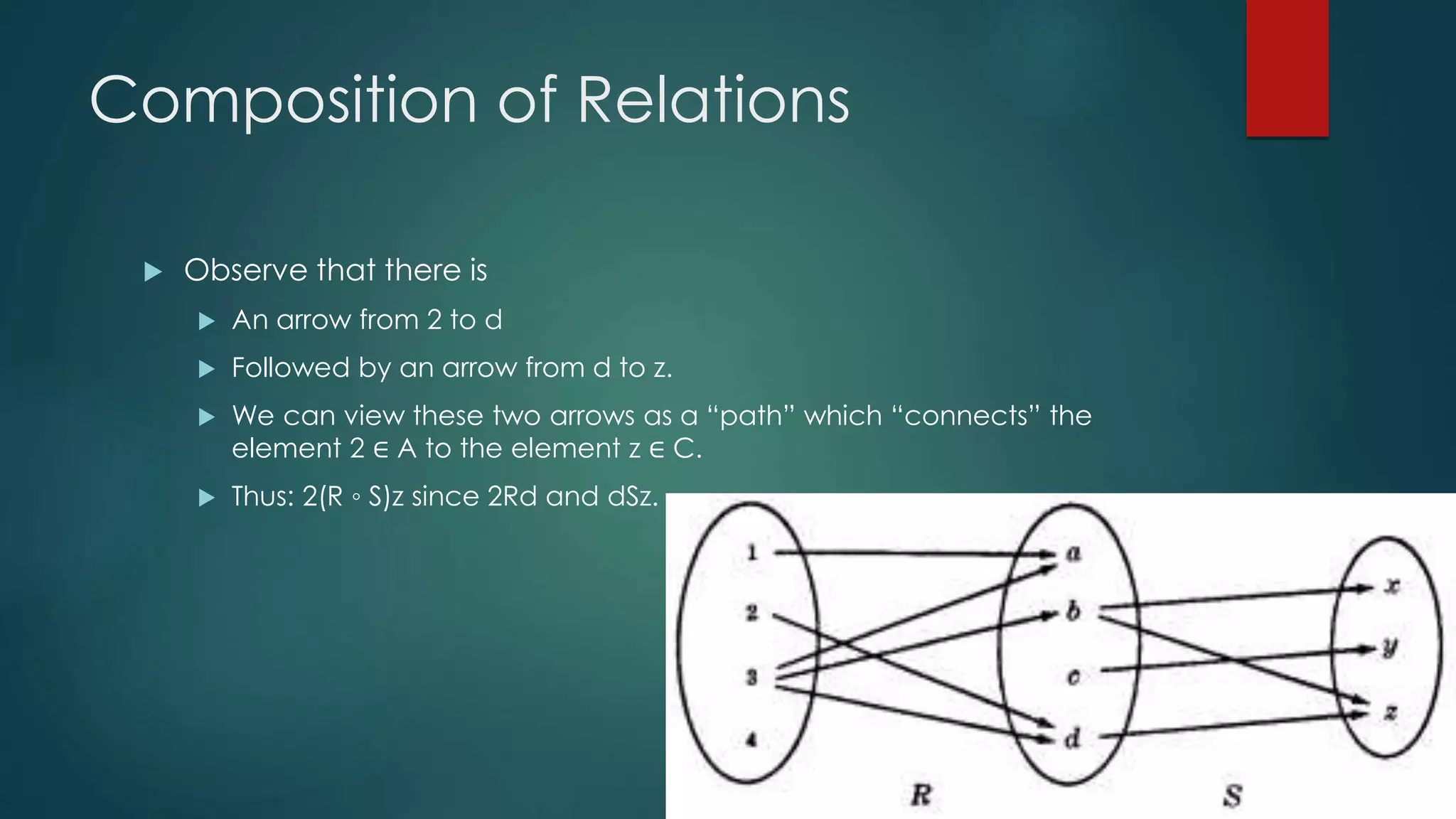
The document discusses different types of relations between elements of sets. It defines relations as subsets of Cartesian products of sets and describes how relations can be represented using matrices or directed graphs. It then introduces various properties of relations such as reflexive, symmetric, transitive, and defines what it means for a relation to have each property. Composition of relations is also covered, along with how relation composition can be represented by matrix multiplication.
More Related Content
Relations
- 1.
- 2. Agenda Introduction ProductSets Relations Representation of Relations Representation of Relations on Finite Sets Directed Graphs of Relations on Sets Composition of Relations Composition of Relations on Matrices Types of Relations Closure Properties Equivalence Relations Partial Ordering Relations n-Ary relations
- 3. Introduction Relationships betweenelements of sets occur in many contexts e.g. business and its telephone number an employee and his or her salary a person and a relative Mathematical Relations e.g. a positive integer and one that it divides a real number and one that is larger than it
- 4. Introduction Relationships betweenelements of sets are represented using the structure called a relation which is just a subset of the Cartesian product of the sets Relations can be used to solve problems such as Determining which pairs of cities are linked by airline flights in a network, Finding a viable order for the different phases of a complicated project Producing a useful way to store information in computer databases
- 5. Product Sets Definition Let A and B be sets. A binary relation from A to B is a subset of A × B. Consider two arbitrary sets A and B. The set of all ordered pairs (a, b) where a ∈ A and b ∈ B is called the product, or Cartesian product, of A and B. A short designation of this product is A × B, which is read “A cross B.” By definition, A × B = {(a, b)| a ∈ A and b ∈ B}
- 6. Relations A binaryrelation from A to B is a set R of ordered pairs where the first element of each ordered pair comes from A and the second element comes from B. We use the notation aRb to denote that (a,b) ∈ R and aRb to denote that (a,b)∉R. Moreover, when (a,b) belongs to R, a is said to be related to b by R.
- 8. Relations Example LetA = {1, 2} and B = {a, b, c}. Then A × B = {(1, a), (1, b), (1, c), (2, a), (2, b), (2, c)} B × A = {(a, 1), (b, 1), (c, 1), (a, 2), (b, 2), (c, 2)} A2 = A × A = {(1, 1), (1, 2), (2, 1), (2, 2)} There are two things worth noting in the above examples. First of all A×B = B ×A. The Cartesian product deals with ordered pairs, so naturally the order in which the sets are considered is important. Secondly, using n(S) for the number of elements in a set S, we have: n(A × B) = 6 = 2(3) = n(A) x n(B) there are n(A) possibilities for a, and for each of these there are n(B) possibilities for b.
- 9. Relations The domainof a relation R is the set of all first elements of the ordered pairs which belong to R, A × B = {(1, a), (1, b), (1, c), (2, a), (2, b), (2, c)} {1,2} the range is the set of second elements. A × B = {(1, a), (1, b), (1, c), (2, a), (2, b), (2, c)} {a,b,c}
- 10. Relations The ideaof a product of sets can be extended to any finite number of sets. For any sets A1, A2,...,An, the set of all ordered n-tuples (a1, a2,...,an) where a1 ∈ A1, a2 ∈ A2,...,an ∈ An is called the product of the sets A1,...,An and is denoted by A1 × A2 ×···× An
- 11. Relations Inverse Relations Let R be any relation from a set A to a set B. The inverse of R, denoted by R−1, is the relation from B to A which consists of those ordered pairs which, when reversed, belong to R; that is, R−1 = {(b, a)|(a, b) ∈ R} For example, Let A = {1, 2, 3} and B = {x, y, z}. Then the inverse of R = {(1, y), (1, z), (3, y)} is R−1 = {(y, 1), (z, 1), (y, 3)} If R is any relation, then (R−1)−1 = R. Domain and range of R−1 are equal, respectively, to the range and domain of R. If R is a relation on A, then R−1 is also a relation on A.
- 12. Representing a Relation Rectangular Array or Matrix Representation Form a rectangular array (matrix) whose Rows are labeled by the elements of A Columns are labeled by the elements of B. Put a 1 or 0 in each position of the array according as a ∈ A is or is not related to b ∈ B. This array is called the matrix of the relation.
- 13. Representing a Relation Matrix Representation Example Let A = {0, 1, 2} and B = {a, b}. Then {(0, a), (0, b), (1, a), (2, b)} is a relation from A to B. This means, for instance, that 0Ra, but that 1R b.
- 14. Representing a Relation Write down the elements of A and the elements of B in two disjoint disks Then draw an arrow from a ∈ A to b ∈ B whenever a is related to b. This picture will be called the arrow diagram of the relation
- 15. Representing a Relation Matrix Representation Example Let A = {0, 1, 2} and B = {a, b}. Then {(0, a), (0, b), (1, a), (2, b)} is a relation from A to B. This means, for instance, that 0Ra, but that 1R b.
- 16. Representing a Relation Directed Graphs of Relations on Sets First we write down the elements of the set Then we draw an arrow from each element x to each element y whenever x is related to y. Let t A = {1, 2, 3, 4}. Then relation R on the set A be R = {(1, 2), (2, 2), (2, 4), (3, 2), (3, 4), (4, 1), (4, 3)} Observe that there is an arrow from 2 to itself, since 2 is related to 2 under R.
- 19. Composition of Relations Let A, B and C be sets, and let R be a relation from A to B and let S be a relation from B to C. That is, R is a subset of A × B and S is a subset of B × C. Then R and S give rise to a relation from A to C denoted by R◦S and defined by: a(R◦S)c if for some b ∈ B we have aRb and bSc R ◦ S = {(a, c)| there exists b ∈ B for which (a, b) ∈ R and (b, c) ∈ S}
- 20. Composition of Relations The composite of R and S is the relation consisting of ordered pairs (a, c), where a∈A, c∈C, and for which there exists an element b ∈ B such that (a, b) ∈ R and (b, c) ∈ S. The relation R◦S is called the composition of R and S; it is sometimes denoted simply by RS Suppose R is a relation on a set A, that is, R is a relation from a set A to itself. Then R◦R, the composition of R with itself, is always defined. Also, R◦R is sometimes denoted by R2. Similarly, R3 = R2◦R = R◦R◦R, and so on. Thus Rn is defined for all positive n.
- 21. Composition of Relations Example Let A = {1, 2, 3, 4}, B = {a, b, c, d}, C = {x, y, z} and let R = {(1, a), (2, d), (3, a), (3, b), (3,d)} and S = {(b, x), (b, z), (c, y), (d, z)}
- 22. Composition of Relations Observe that there is An arrow from 2 to d Followed by an arrow from d to z. We can view these two arrows as a “path” which “connects” the element 2 ∈ A to the element z ∈ C. Thus: 2(R ◦ S)z since 2Rd and dSz.
- 23. Composition of Relationsand Matrices If S consists of ordered pairs , then the ordered pairs satisfy some given equation E(x, y) = 0 Let MR and MS denote respectively the matrix representations of the relations R and S. Then
- 24. Composition of Relationsand Matrices Multiplying MR and MS we obtain the matrix The nonzero entries in this matrix tell us which elements are related by R◦S. Thus M = MRMS and MR◦S have the same nonzero entries.
- 25. Types or Typesof Relations Reflexive Relations Irreflexive Relations Symmetric Relations Asymmetric Relations Antisymmetric Relations Transitive Relations
- 26. Reflexive Relation Areflexive relation is a binary relation on a set for which every element is related to itself. relation R on a set A is called reflexive If (a, a) ∈ R for every element a ∈ A. A relation R on a set A is called reflexive If there exists an a ∈ A for which (a, a) ∉ R
- 27. Reflexive Relation Example Consider the following five relations on the set A = {1, 2, 3, 4}: R1 = {(1, 1), (1, 2), (2, 3), (1, 3), (4, 4)} R2 = {(1, 1)(1, 2), (2, 1), (2, 2), (3, 3), (4, 4)} R3 = {(1, 3), (2, 1)} R4 = ∅, the empty relation R5 = A × A, the universal relation Since A contains the four elements 1, 2, 3, and 4, A relation R on A is reflexive if it contains the four pairs (1, 1), (2, 2), (3, 3), and (4, 4). Thus only R2 and the universal relation R5 = A × A are reflexive. Note that R1, R3, and R4 are not reflexive since, for example, (2, 2) does not belong to any of them.
- 28. Ir-reflexive or Anti-Reflexive A relation that is irreflexive, or anti-reflexive, is a binary relation on a set where no element is related to itself. A relation R on a set A is called irreflexive If (a, a) ∉ R for every element a ∈ A. A relation R on a set A is not irreflexive If there exists an at least one a ∈ A for which (a,a) ∈ R
- 29. Symmetric Relation Arelation R on a set A is symmetric if whenever aRb then bRa, that is, if whenever (a, b) ∈ R then (b, a) ∈ R. R is not symmetric if there exists a, b ∈ A such that (a, b) ∈ R but (b, a) ∉ R.
- 30. Anti Symmetric Relation A relation R on a set A is antisymmetric if whenever aRb and bRa then a = b, that is, if a ≠ b and aRb then bRa. R is not antisymmetric if there exist distinct elements a and b in A such that aRb and bRa.
- 31. Asymmetric Relation LetR be a relation on A. Then R is called asymmetric if (x,y)∈R always implies (y,x)∉R: R is asymmetric: ∀x∈A ∀y∈A ∈ R (y,x) ∉R.
- 32. Transitive Relation Arelation R on a set A is transitive if whenever aRb and bRc then aRc, that is, if whenever (a, b), (b, c) ∈ R then (a, c) ∈ R. Thus R is not transitive if there exist a, b, c ∈ R such that (a, b), (b, c) ∈ R but (a, c) ∉ R.