The document provides an overview of the simplex method for solving linear programming problems. It discusses:
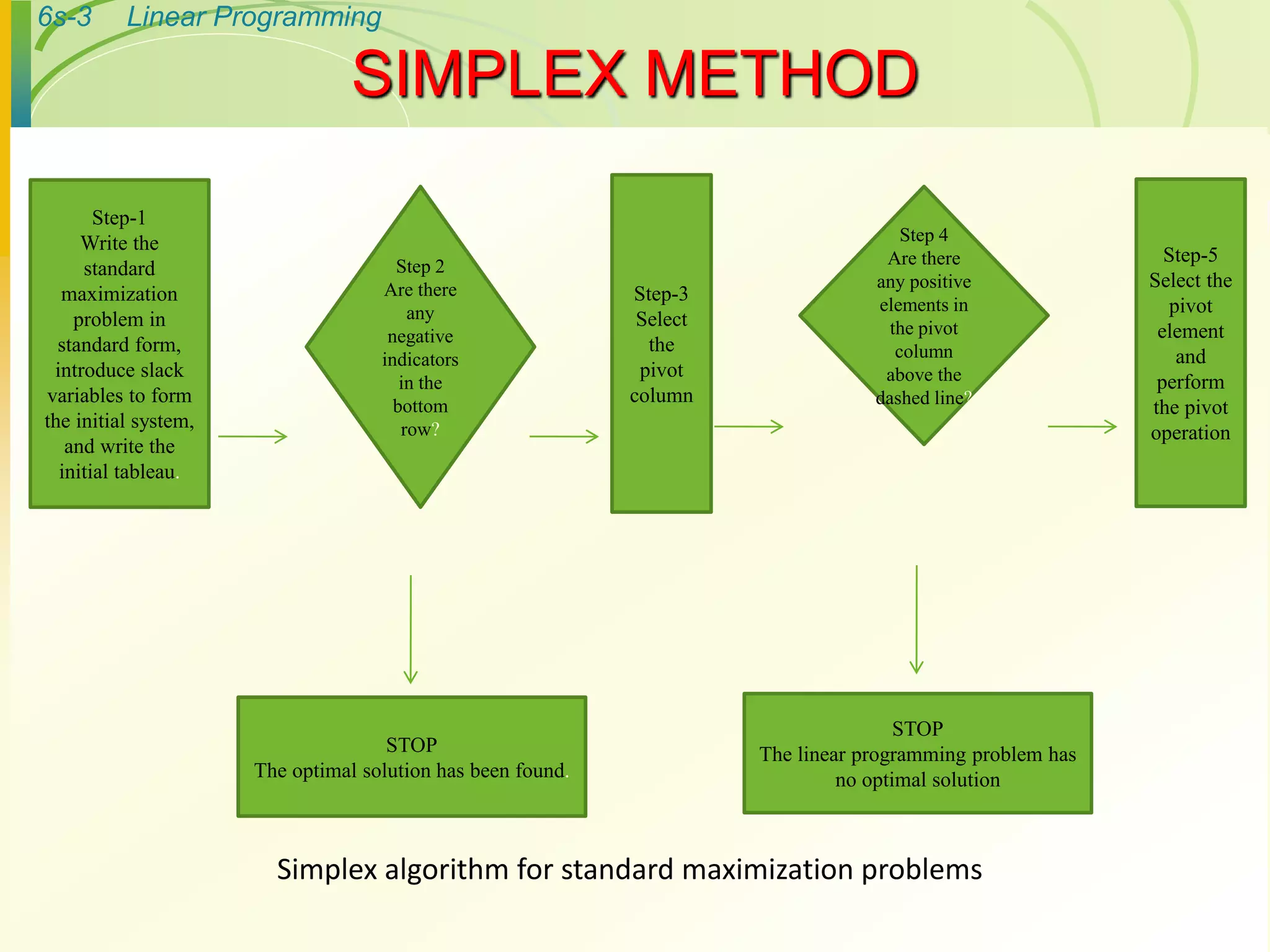
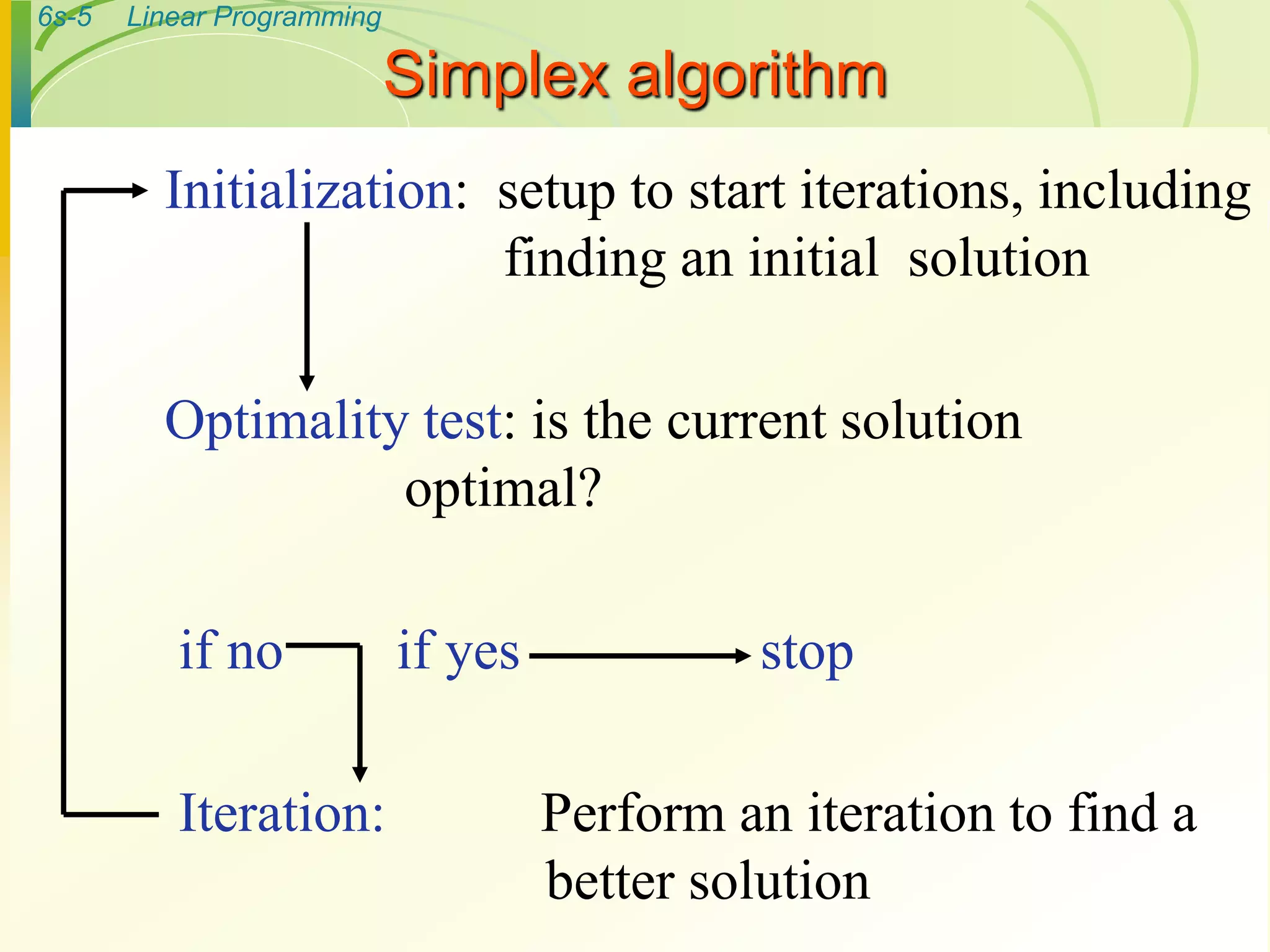
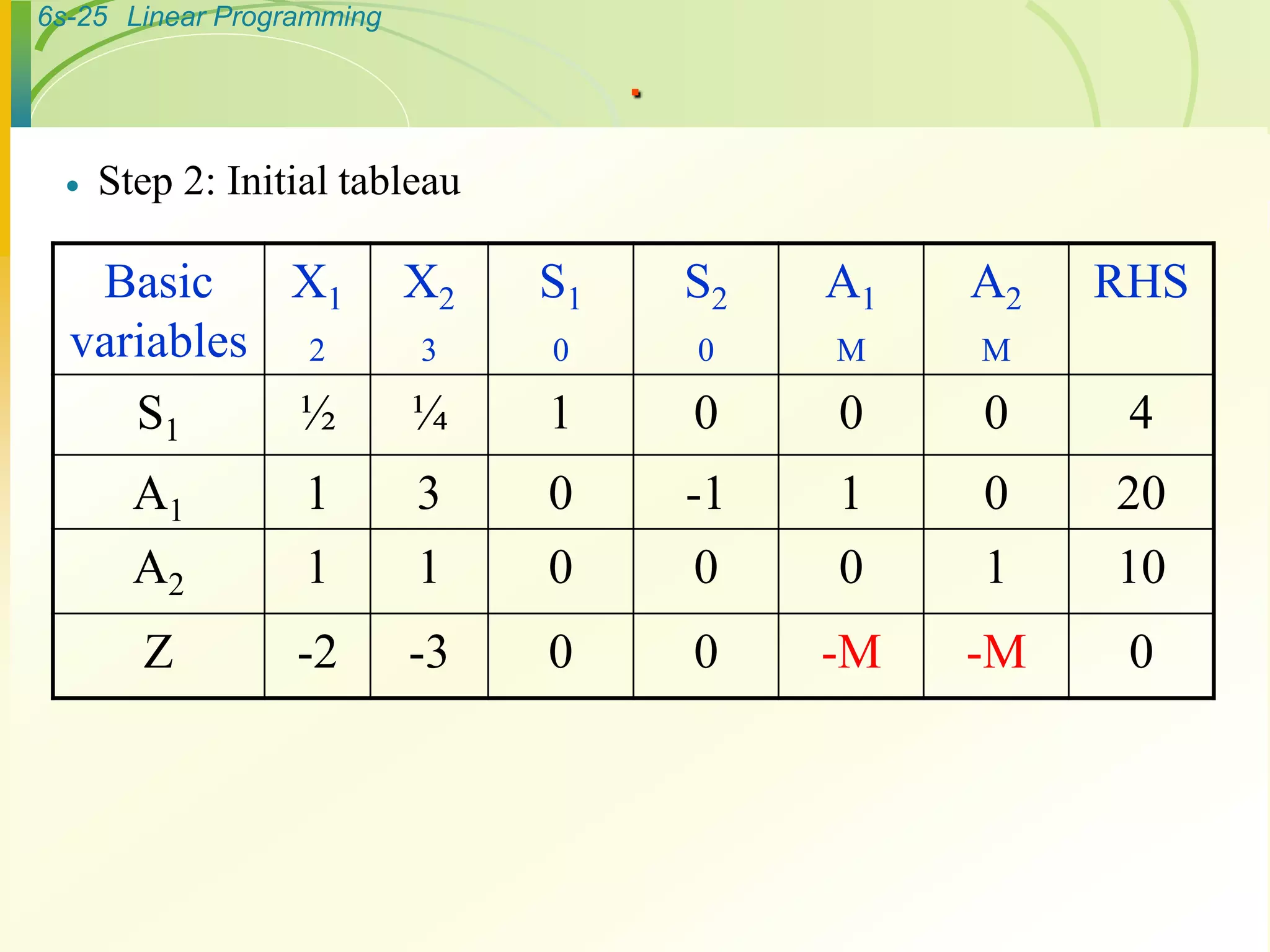
- The simplex method is an iterative algorithm that generates a series of solutions in tabular form called tableaus to find an optimal solution.
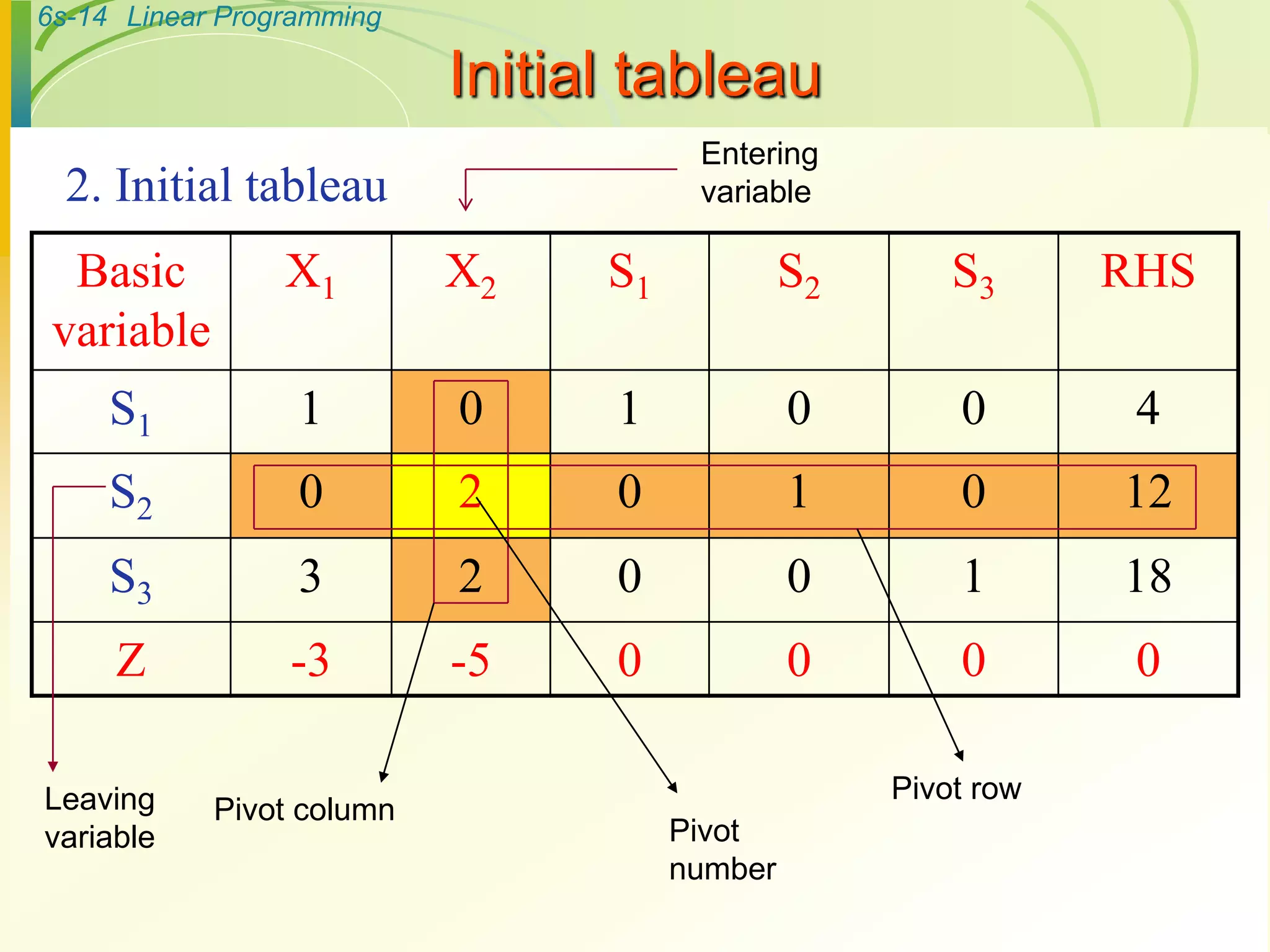
- It involves writing the problem in standard form, introducing slack variables, and constructing an initial tableau.
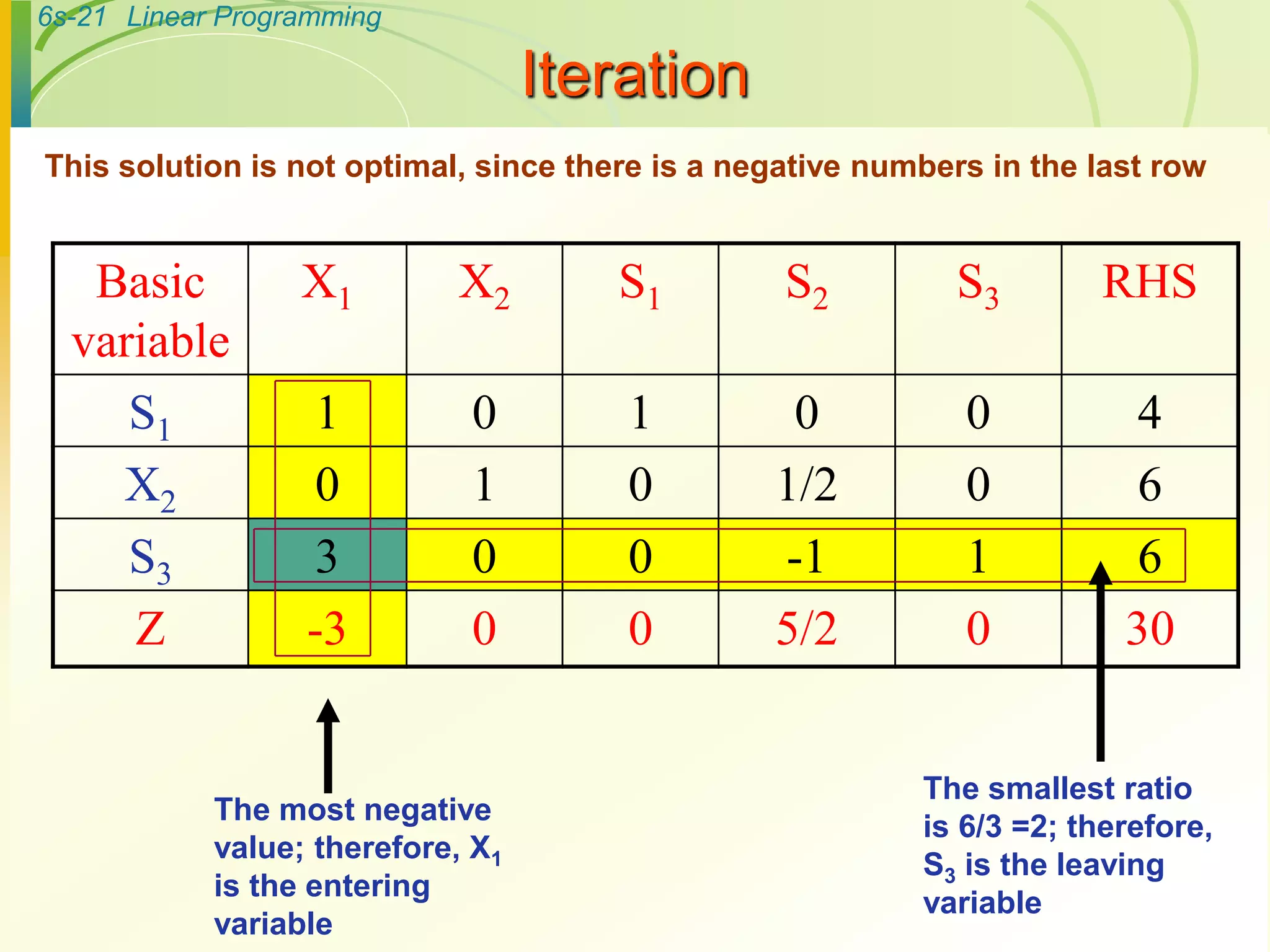
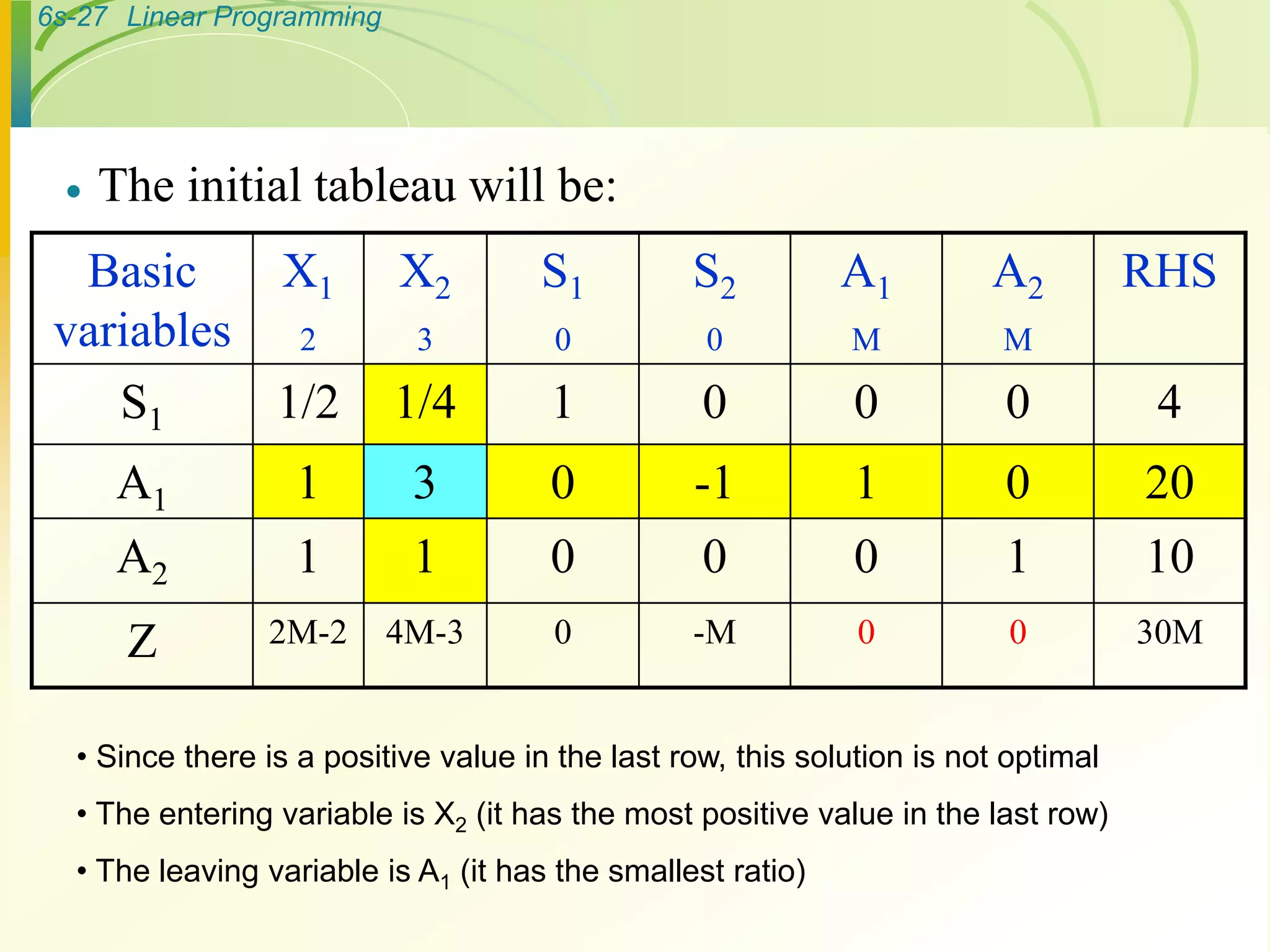
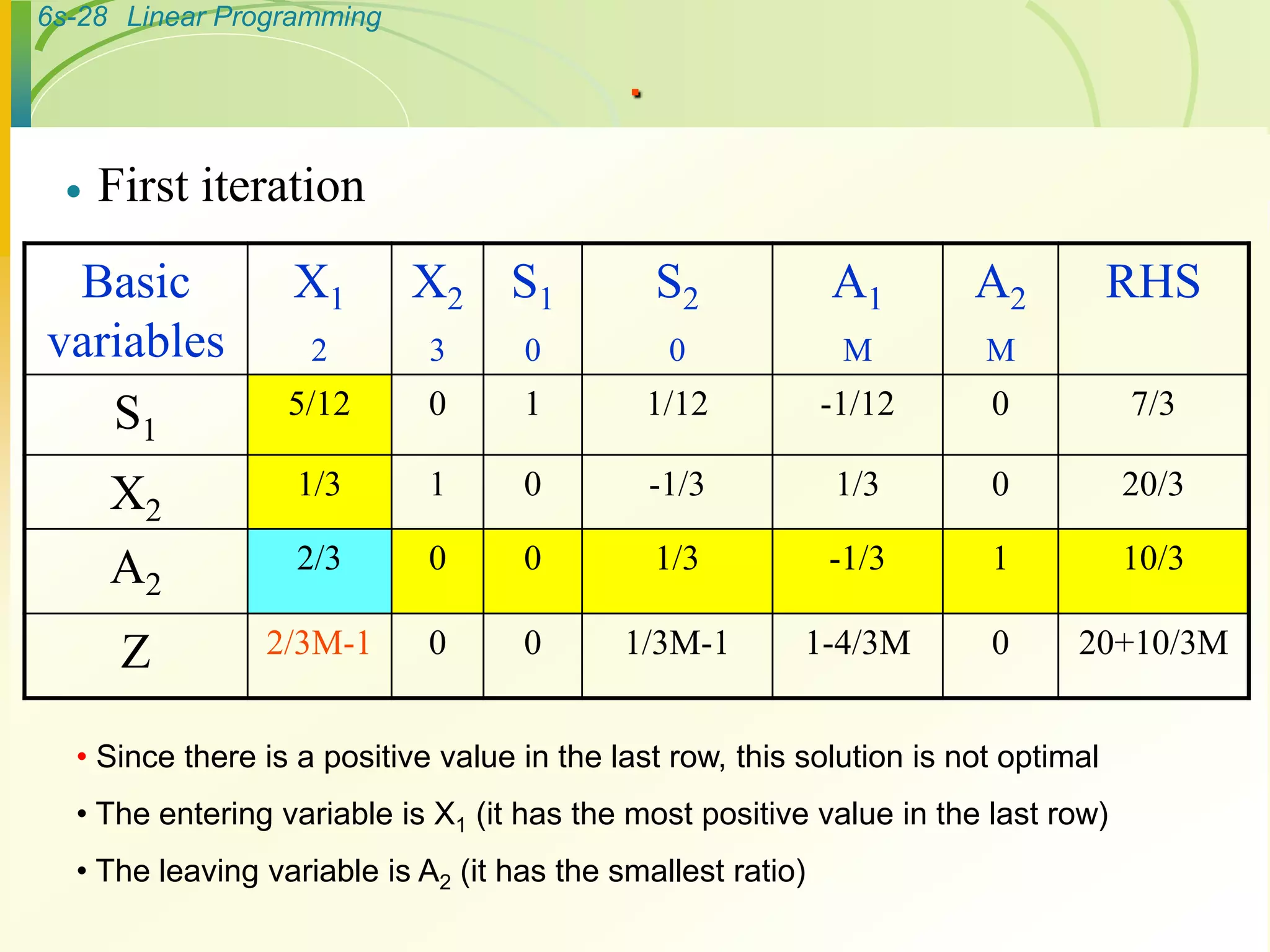
- The method then performs iterations involving selecting a pivot column and row, and applying row operations to generate new tableaus until an optimal solution is found.
- It also discusses how artificial variables are introduced for problems with non-strict inequalities and provides an example solved using the simplex method.