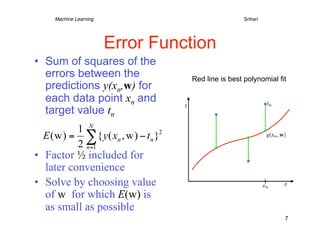
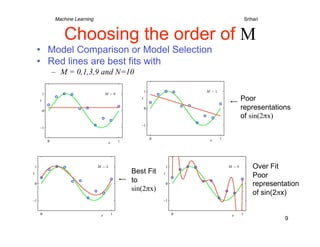
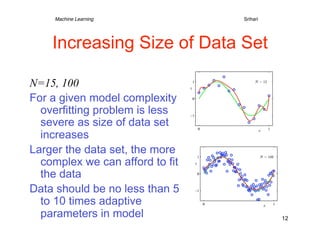
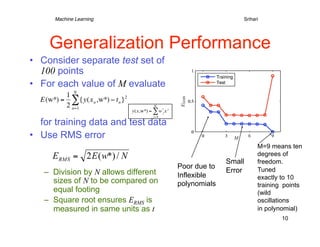
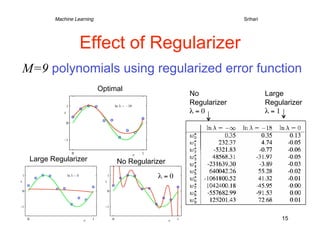
1) The document discusses machine learning concepts including polynomial curve fitting, probability theory, maximum likelihood, Bayesian approaches, and model selection. 2) It describes using polynomial functions to fit a curve to data points and minimizing the error between predictions and actual target values. Higher order polynomials can overfit noise in the data. 3) Regularization is introduced to add a penalty for high coefficient values in complex models to reduce overfitting, analogous to limiting the polynomial order. This improves generalization to new data.

1. Machine Learning
Srihari
Basic Concepts in Machine
Learning
Sargur N. Srihari
1

2. Machine Learning
Srihari
Introduction to ML: Topics
1. Polynomial Curve Fitting
2. Probability Theory of multiple variables
3. Maximum Likelihood
4. Bayesian Approach
5. Model Selection
6. Curse of Dimensionality
2

3. Machine Learning
Srihari
Polynomial Curve Fitting
Sargur N. Srihari
3

4. Machine Learning
Srihari
Simple Regression Problem
• Observe Real-valued
input variable x
• Use x to predict value
of target variable t
Target
• Synthetic data Variable
generated from
sin(2π x)
• Random noise in
Input Variable
target values
4

5. Machine Learning
Srihari
Notation
• N observations of x
x = (x1,..,xN)T
t = (t1,..,tN)T
• Goal is to exploit training
set to predict value of
from x
Data Generation:
• Inherently a difficult N = 10
problem Spaced uniformly in range [0,1]
Generated from sin(2πx) by adding
• Probability theory allows small Gaussian noise
us to make a prediction Noise typical due to unobserved variables
5

6. Machine Learning
Srihari
Polynomial Curve Fitting
• Polynomial function
• Where M is the order of the polynomial
• Is higher value of M better? We’ll see shortly!
• Coefficients w0 ,…wM are denoted by vector w
• Nonlinear function of x, linear function of
coefficients w
• Called Linear Models
6

7. Machine Learning
Srihari
Error Function
• Sum of squares of the
errors between the Red line is best polynomial fit
predictions y(xn,w) for
each data point xn and
target value tn
• Factor ½ included for
later convenience
• Solve by choosing value
of w for which E(w) is
as small as possible
7

8. Machine Learning
Srihari
Minimization of Error Function
• Error function is a quadratic in
coefficients w
• Derivative with respect to Since y(x,w) = ∑ w j x j
M
coefficients will be linear in
j= 0
elements of w
∂E(w) N
= ∑{y(x n ,w) − t n }x n
i
• Thus error function has a unique ∂w i n=1
minimum denoted w*
N M
= ∑{∑ w j x nj − t n }x n
i
n =1 j=0
• Resulting polynomial is y(x,w*) Setting equal to zero
N M N
∑∑w j x i+ j
n = ∑ tn x n
i
n=1 j= 0 n=1
Set of M +1 equations (i = 0,.., M) are
solved to get elements of w *
8
€

9. Machine Learning
Srihari
Choosing the order of M
• Model Comparison or Model Selection
• Red lines are best fits with
– M = 0,1,3,9 and N=10
Poor
representations
of sin(2πx)
Over Fit
Best Fit
Poor
to representation
sin(2πx)
of sin(2πx)
9

10. Machine Learning
Srihari
Generalization Performance
• Consider separate test set of
100 points
• For each value of M evaluate
1 N
E(w*) = ∑{y(x n ,w*) − t n }2
2 n=1 M
y(x,w*) = ∑ w *j x j
j= 0
for training data and test data
€ • Use RMS error €
M=9 means ten
degrees of
Small freedom.
Poor due to Tuned
– Division by N allows different Error
Inflexible exactly to 10
sizes of N to be compared on polynomials training points
equal footing (wild
– Square root ensures ERMS is oscillations
measured in same units as t in polynomial)
10

11. Machine Learning
Srihari
Values of Coefficients w* for
different polynomials of order M
As M increases magnitude of coefficients increases
At M=9 finely tuned to random noise in target values
11

12. Machine Learning
Srihari
Increasing Size of Data Set
N=15, 100
For a given model complexity
overfitting problem is less
severe as size of data set
increases
Larger the data set, the more
complex we can afford to fit
the data
Data should be no less than 5
to 10 times adaptive
parameters in model 12

13. Machine Learning
Srihari
Least Squares is case of Maximum
Likelihood
• Unsatisfying to limit the number of parameters to
size of training set
• More reasonable to choose model complexity
according to problem complexity
• Least squares approach is a specific case of
maximum likelihood
– Over-fitting is a general property of maximum likelihood
• Bayesian approach avoids over-fitting problem
– No. of parameters can greatly exceed no. of data points
– Effective no. of parameters adapts automatically to size of
data set
13

14. Machine Learning
Srihari
Regularization of Least Squares
• Using relatively complex models with data
sets of limited size
• Add a penalty term to error function to
discourage coefficients from reaching
large values • λ determines relative
importance of
regularization term
to error term
• Can be minimized
exactly in closed form
• Known as shrinkage
in statistics
Weight decay in neural
networks 14

15. Machine Learning
Srihari
Effect of Regularizer
M=9 polynomials using regularized error function
Optimal
No Large
Regularizer Regularizer
λ = 0
λ = 1
Large Regularizer No Regularizer
λ = 0
15

16. Machine Learning
Srihari
Impact of Regularization on Error
• λ controls the complexity of the
model and hence degree of over-
fitting
– Analogous to choice of M
• Suggested Approach:
• Training set
– to determine coefficients w M=9 polynomial
– For different values of (M or λ)
• Validation set (holdout)
– to optimize model complexity (M or λ)
16

17. Machine Learning
Srihari
Concluding Remarks on Regression
• Approach suggests partitioning data into training
set to determine coefficients w
• Separate validation set (or hold-out set) to
optimize model complexity M or λ
• More sophisticated approaches are not as
wasteful of training data
• More principled approach is based on probability
theory
• Classification is a special case of regression
where target value is discrete values
17